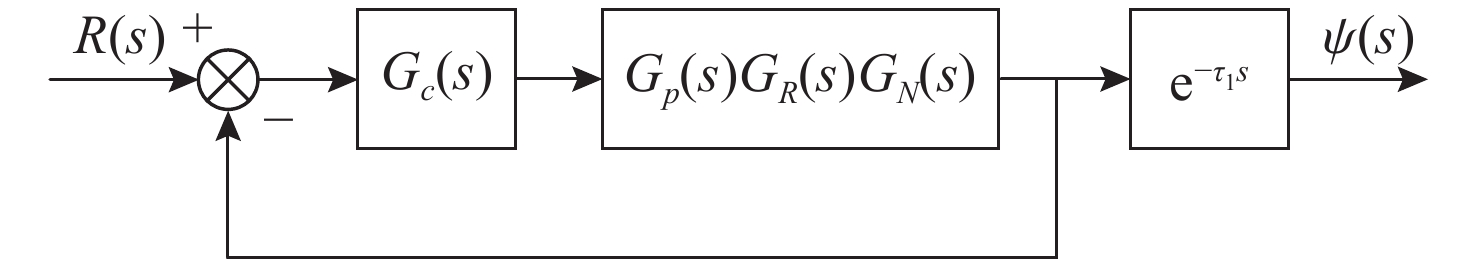改进Smith预估器结合HCOPSO算法的无人船航向控制

李至琦; 刘兰军; 陈家林

doi:10.11993/j.issn.2096-3920.2025-0104

改进Smith预估器结合HCOPSO算法的无人船航向控制

doi: 10.11993/j.issn.2096-3920.2025-0104

李至琦^1,,
刘兰军^{1, 2, ,},
陈家林^{1, 2,}

1.
中国海洋大学工程学院, 山东青岛, 266100
2.
海洋智能装备技术山东省工程研究中心, 山东青岛, 266100

基金项目: 国家重点研发计划项目资助(2017YFC****203).

详细信息

作者简介:
李至琦(2001-), 男, 在读硕士, 主要研究方向为嵌入式技术与智能仪器、无人系统控制

通讯作者:
刘兰军(1979-), 男, 博士, 副教授, 主要研究方向为嵌入式技术与智能仪器、海洋探测与观测技术、水声通信与网络技术.

中图分类号: U674.94; TJ63
计量
- 文章访问数: 9
- HTML全文浏览量: 5
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2025-08-12
- 修回日期: 2025-10-13
- 录用日期: 2025-10-21
- 网络出版日期: 2025-11-05

Optimized Smith Predictor Combined with HCOPSO Algorithm for Unman Surface Vehicle Heading Control

LI Zhiqi^1
,,
LIU Lanjun^{1, 2
, ,},
CHEN Jialin^{1, 2
,}

1.
College of Engineering, Ocean University of China, Qingdao 266100, China
2.
Shandong Provincial Engineering Research Center for Marine Intelligent Equipment Technology, Qingdao 266100, China

摘要

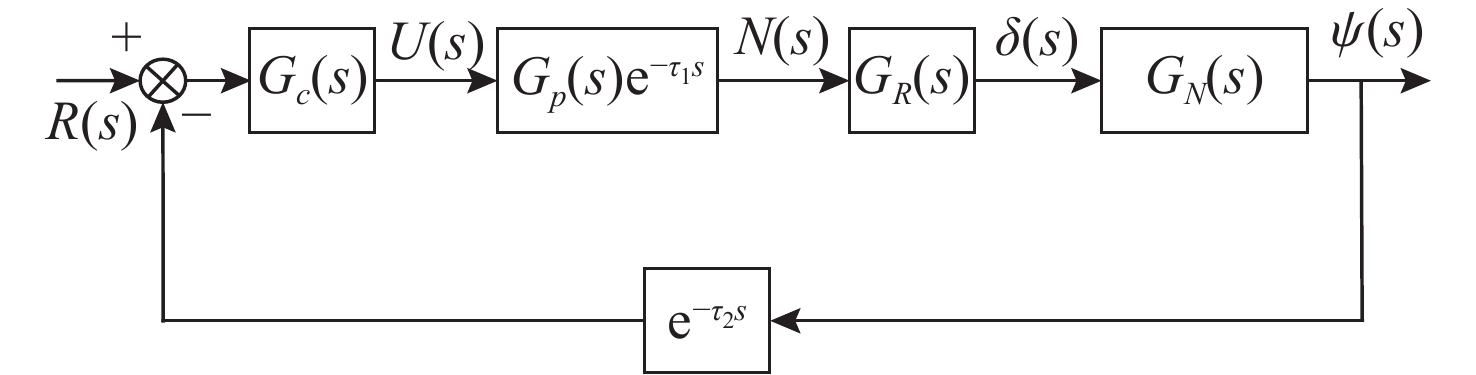
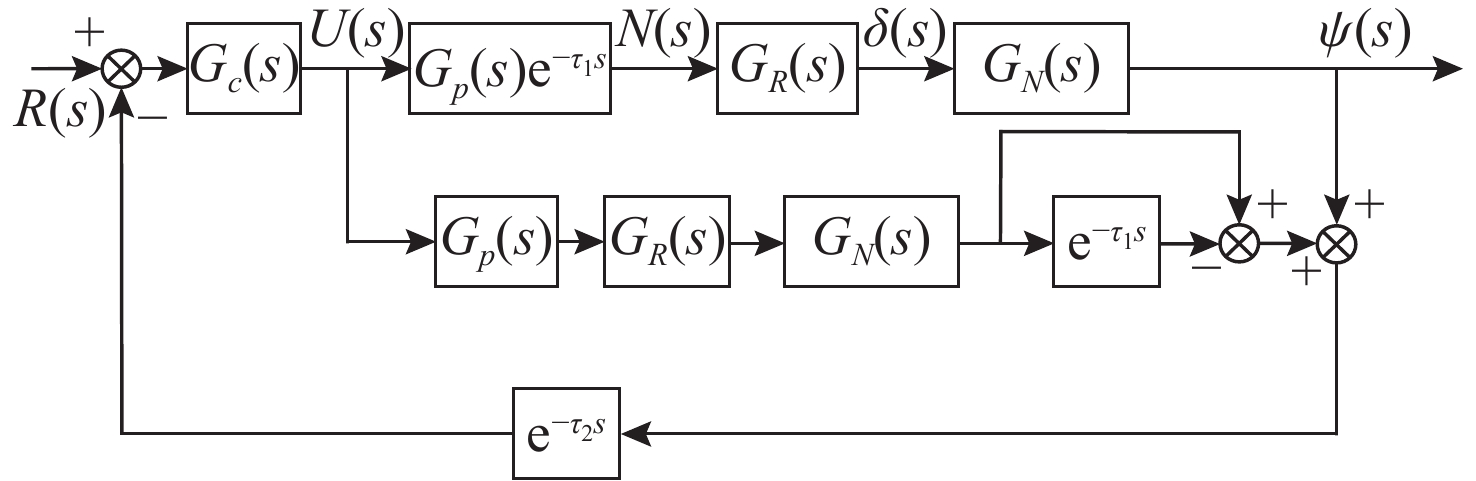
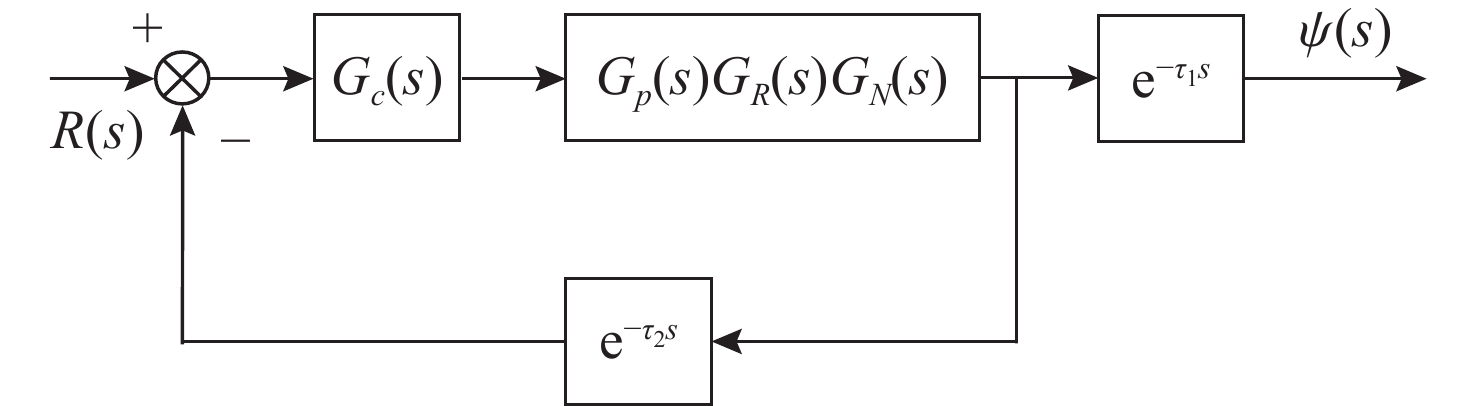
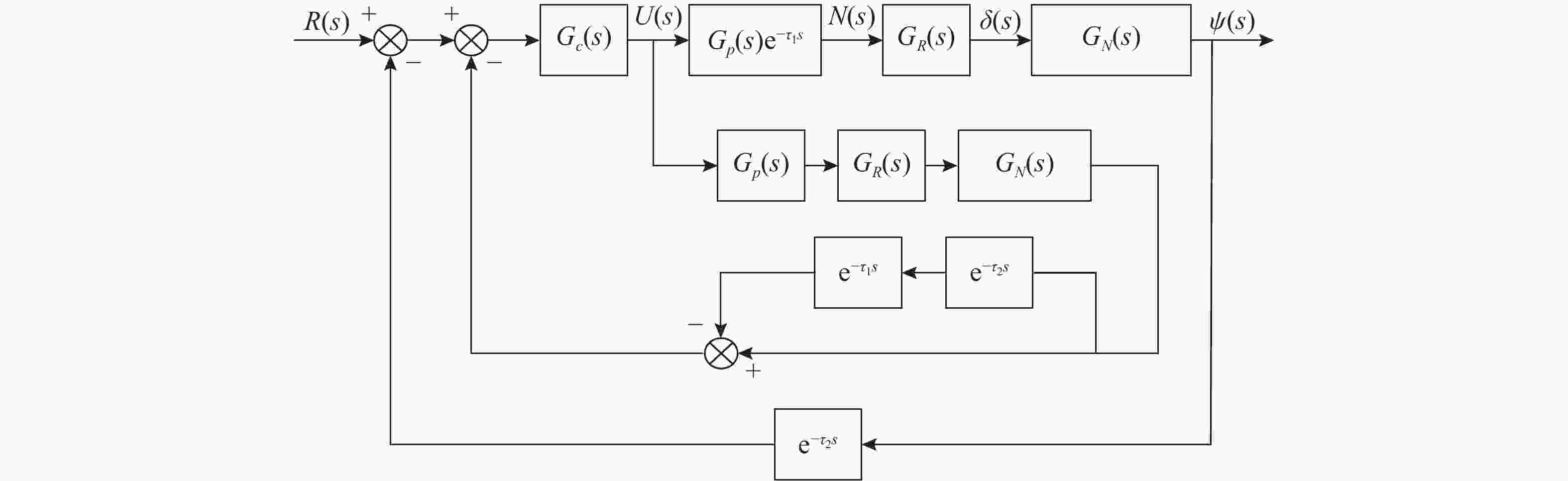
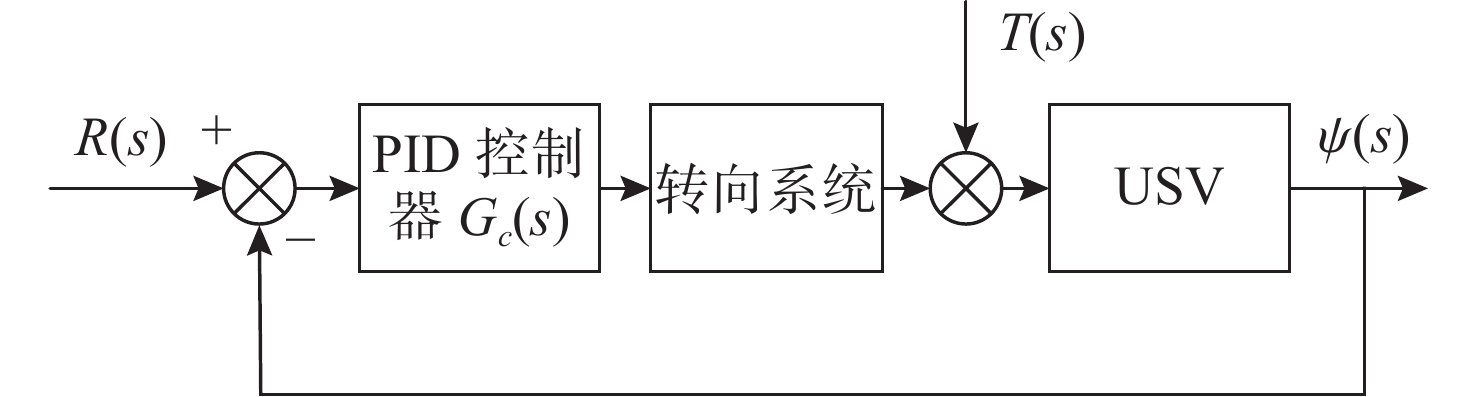
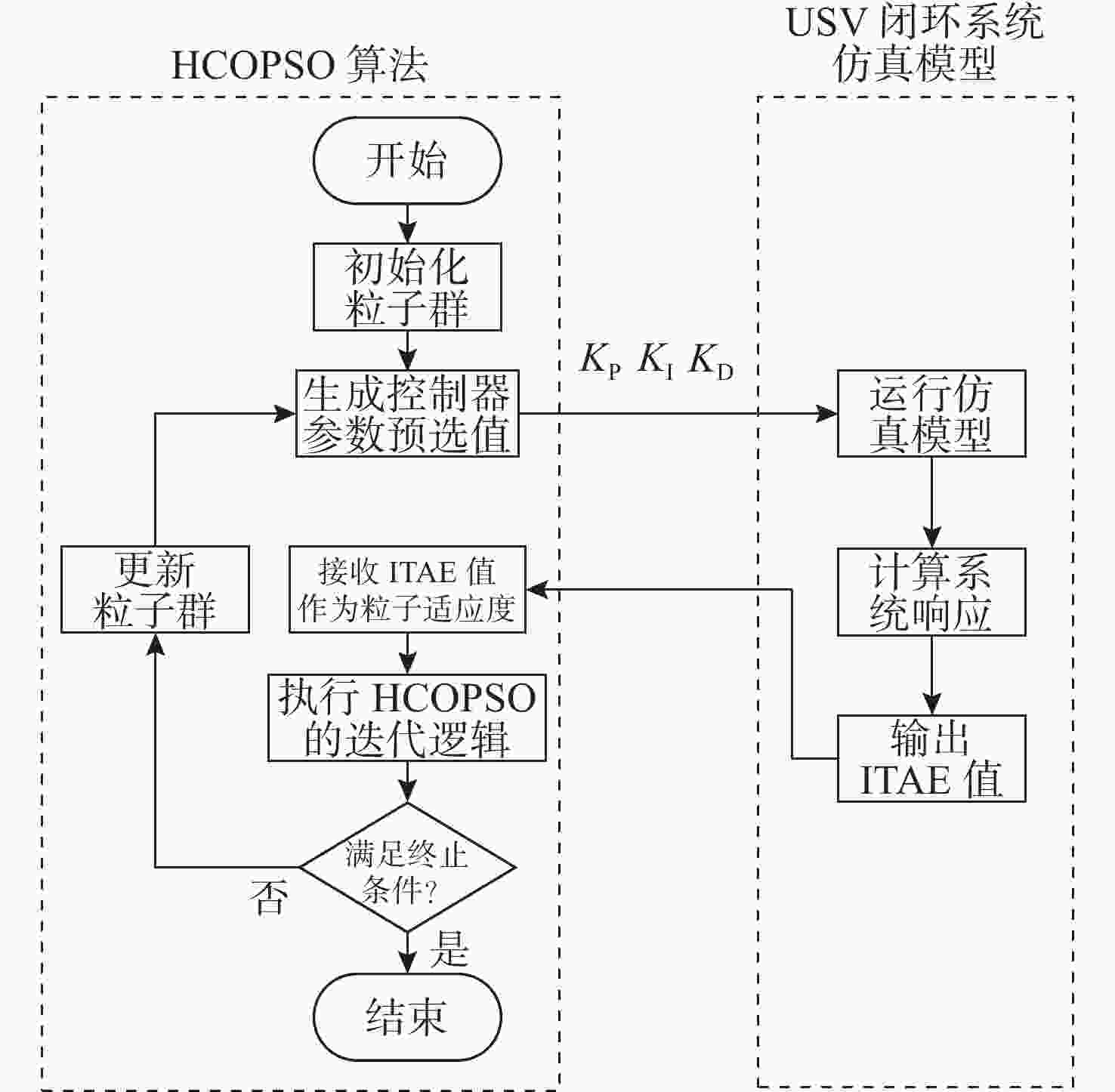
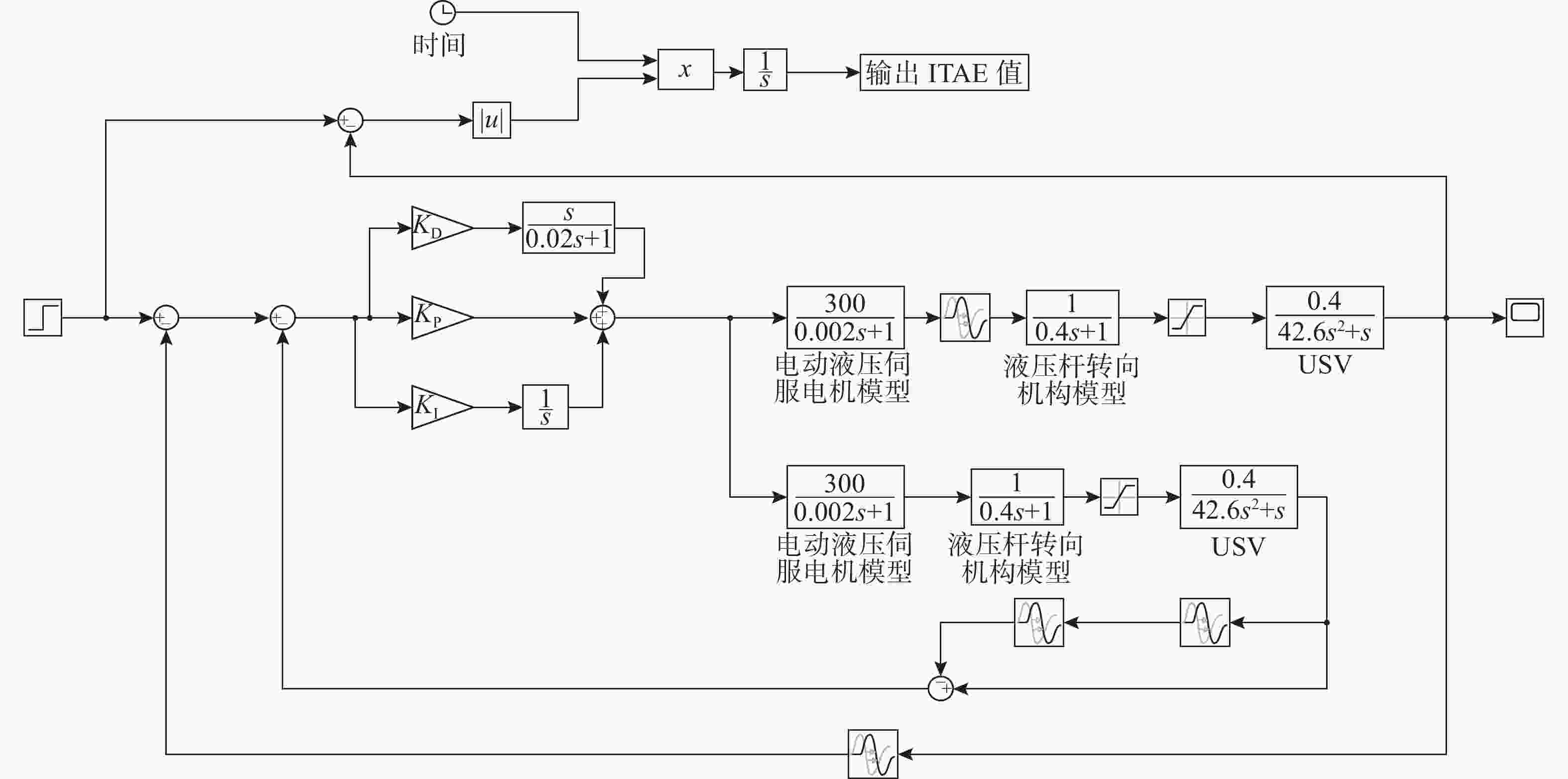
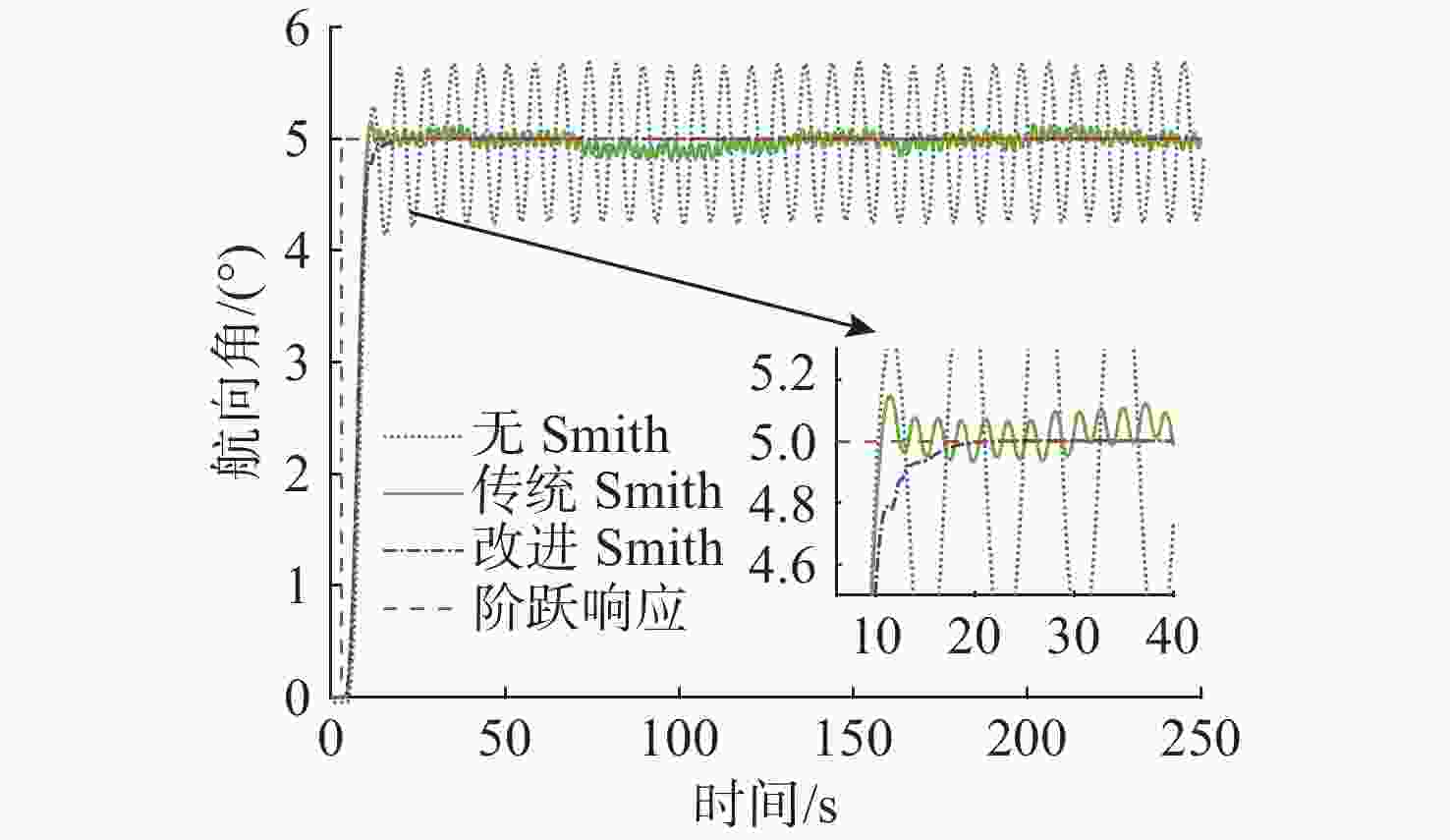
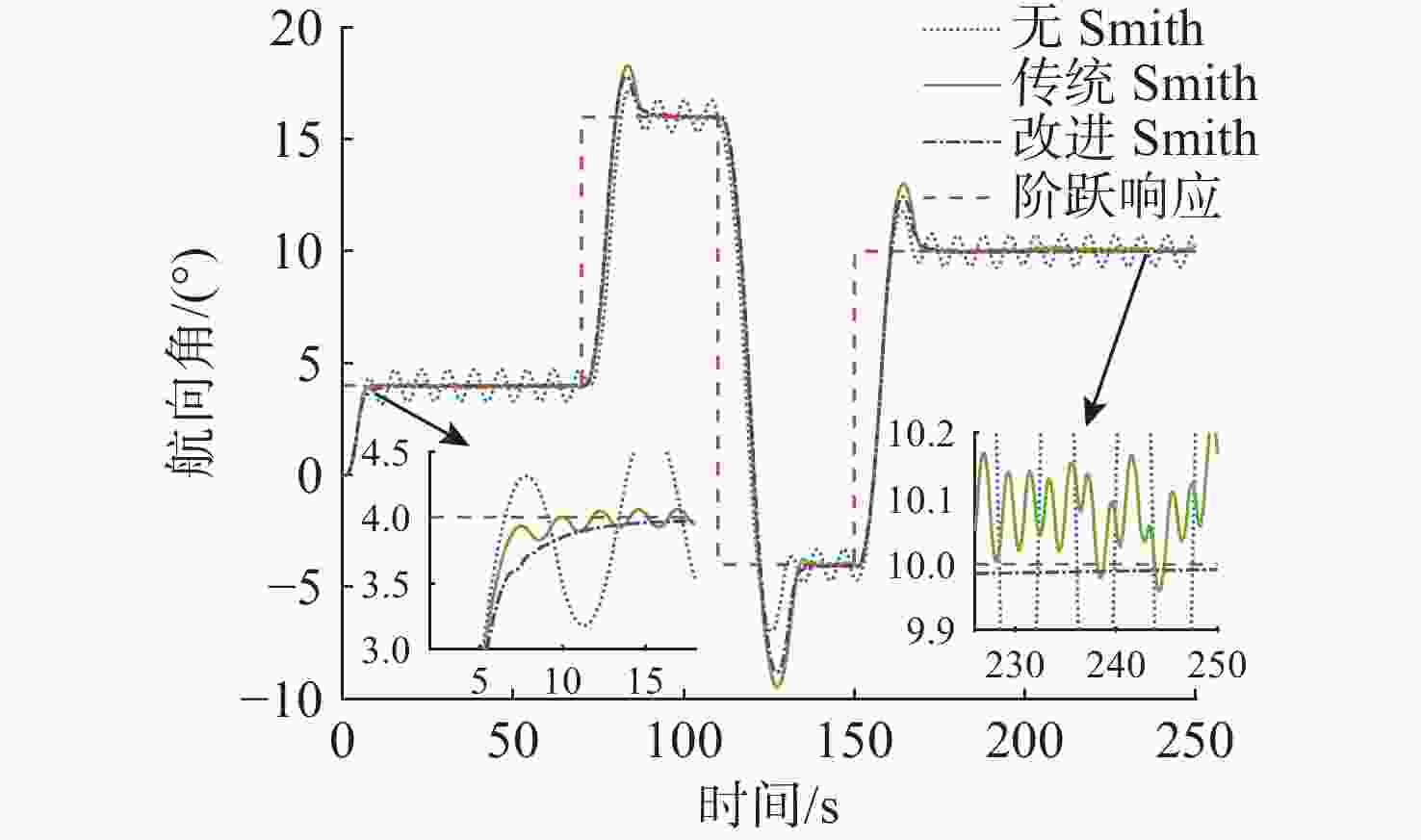
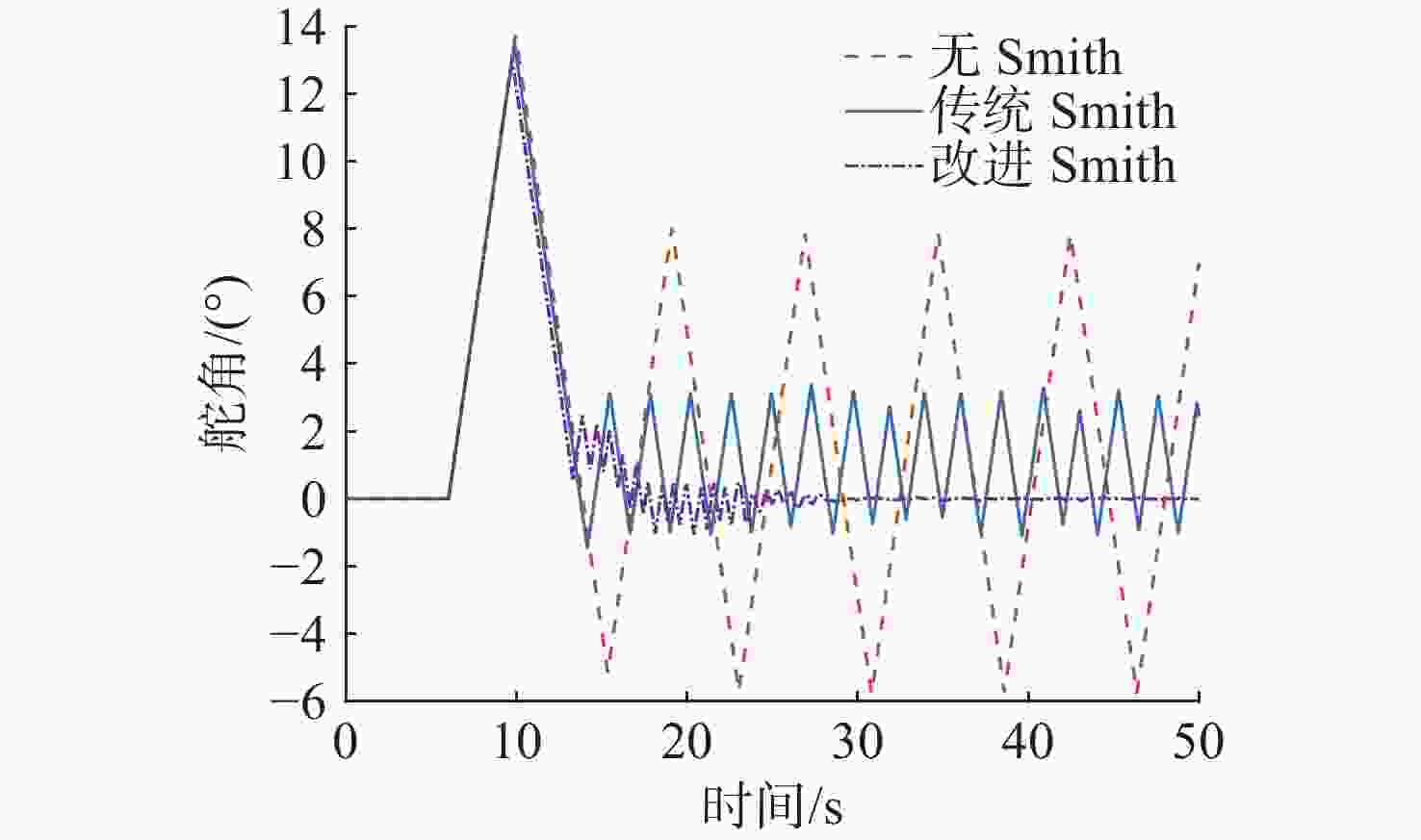
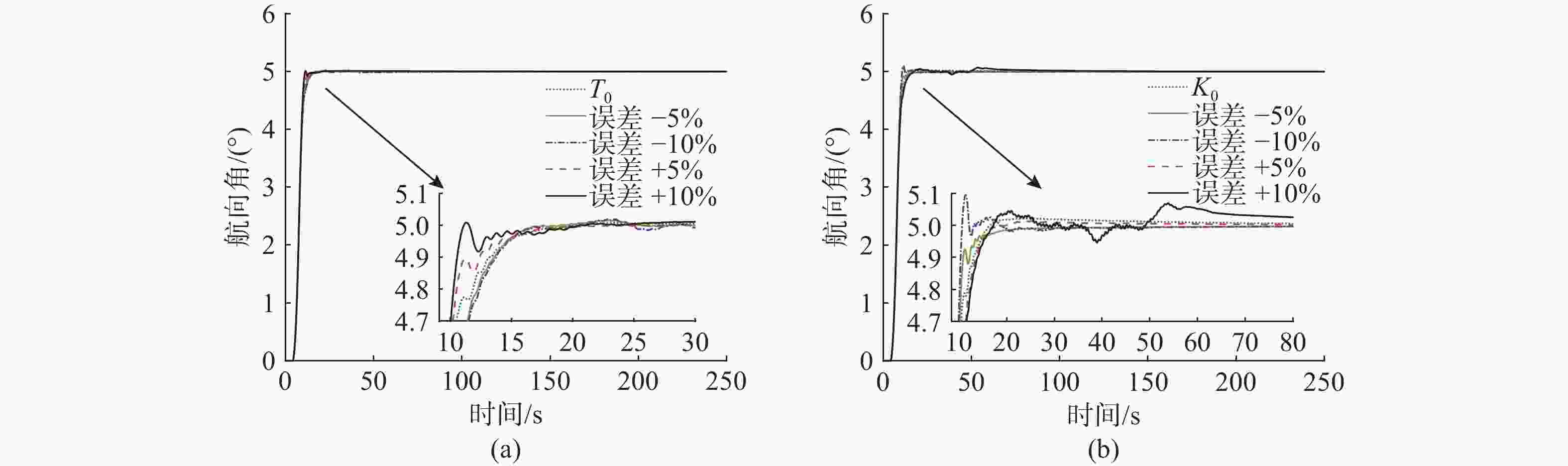
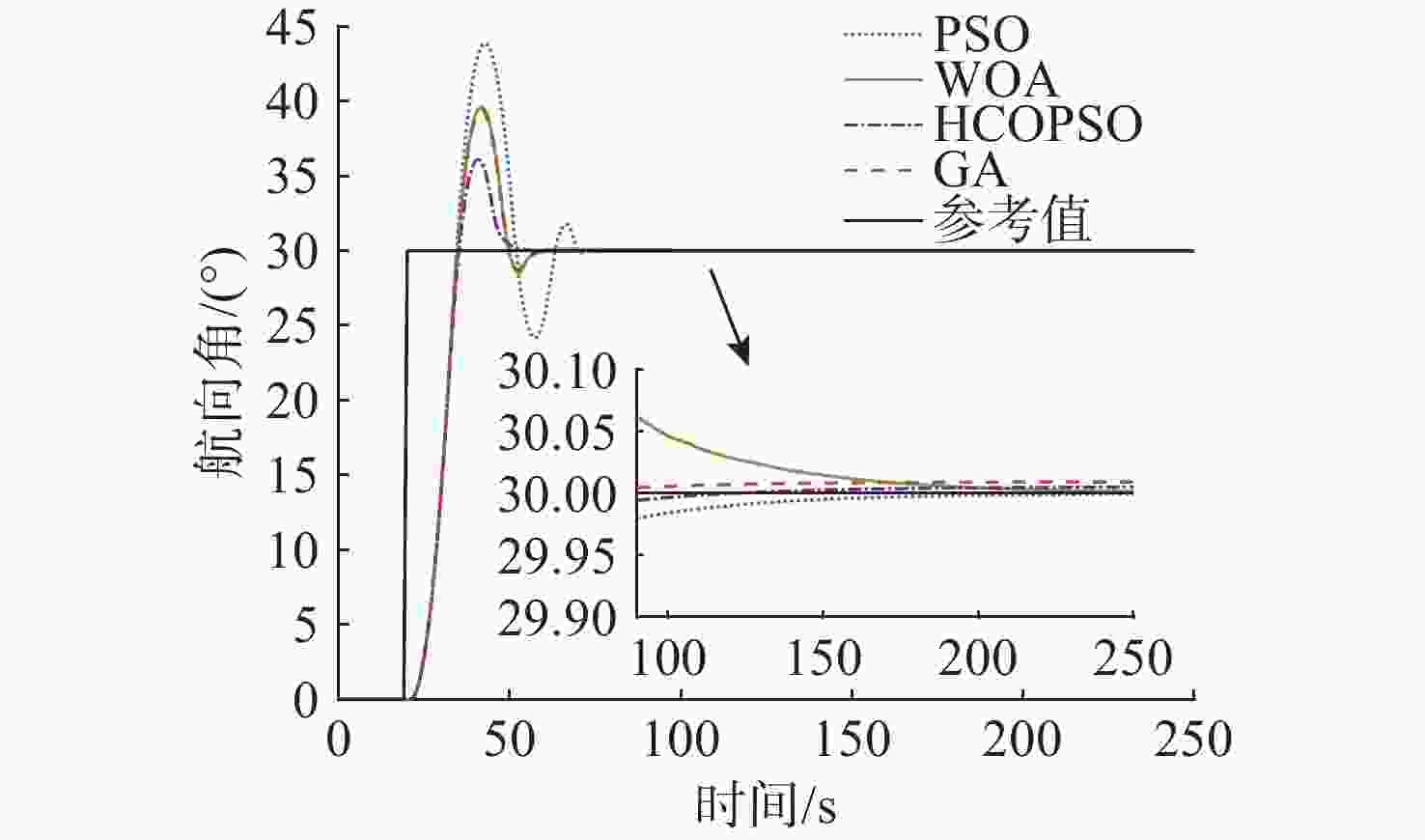
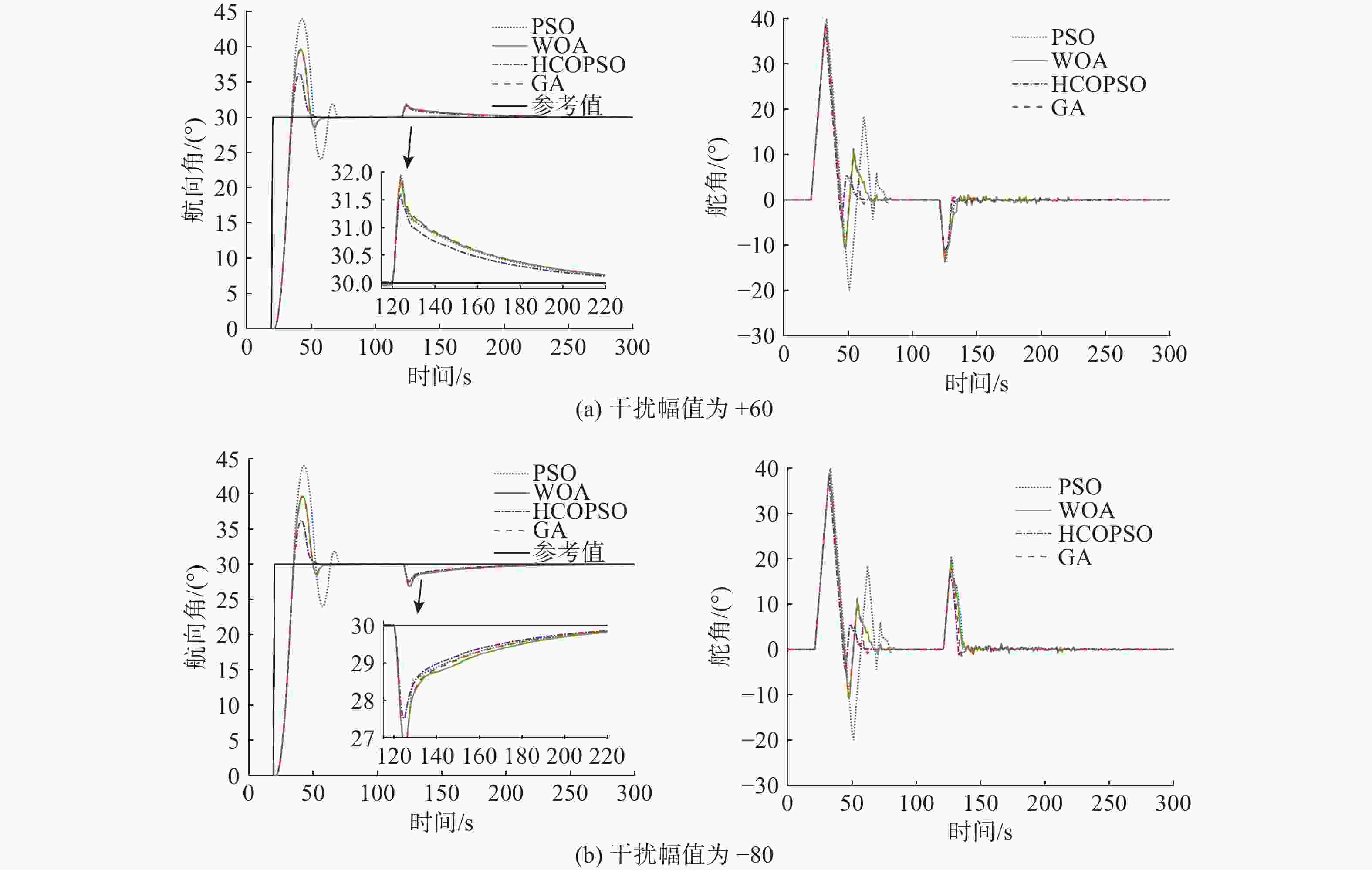
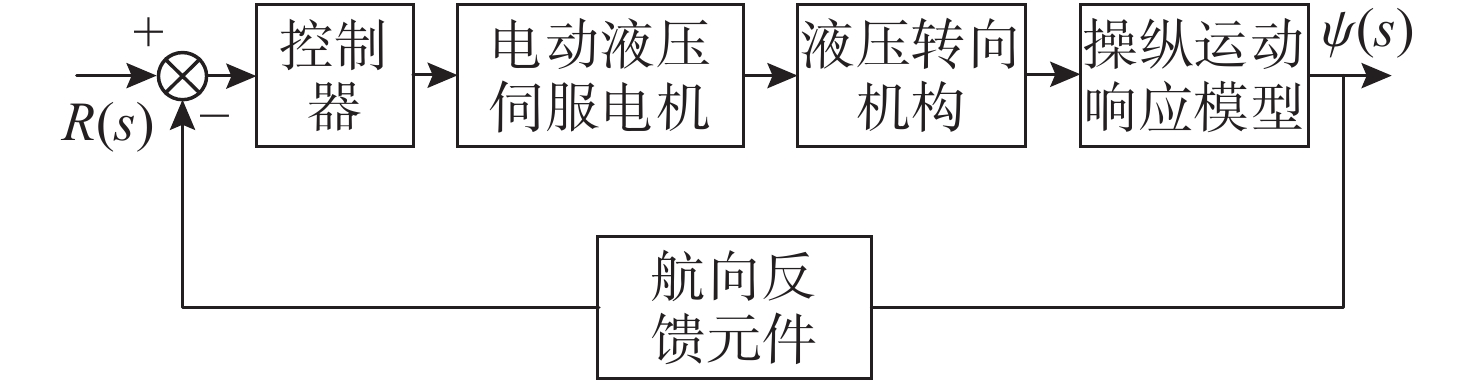
摘要: 高速无人船(USV)航向控制中, 同时存在前向通道与反馈回路的时滞环节, 并且具有较大的延迟/动态时间比, 显著降低航向控制性能。传统Smith预估器能有效补偿前向通道时滞, 但未考虑反馈回路的时滞。为此, 文中将反馈回路时滞纳入Smith预估器设计, 构建包含双向时滞的预测模型, 同时补偿前向通道与反馈回路的时滞, 减少双向时滞的系统相位裕度侵蚀。进一步, 引入混合均值中心反向学习粒子群优化(HCOPSO)算法进行比例-积分-微分(PID)控制器参数寻优整定, 该算法在迭代前期利用均值中心反向学习策略扩大搜索范围, 后期通过自适应压缩因子实现精细寻优, 兼具全局探索与局部开发的优势, 有效解决寻优过程的局部最优解问题。基于无人船航向模型进行了仿真测试, 结果表明, 改进Smith预估PID控制器相较于常规PID控制器、传统Smith预估PID控制器, 使系统的超调量和调节时间均得到了改善, 稳态误差小于0.1°; 并且当改进Smith预估补偿模型存在误差时, 系统依然能够保持良好的动态性能与稳态精度。同时, 针对改进Smith预估PID控制器, 进一步对比分析了HCOPSO算法与粒子群优化算法(PSO)、遗传算法(GA)、鲸鱼优化算法(WOA)的参数寻优, 对比分析了环境干扰下HCOPSO算法与其他算法的航向控制性能。结果表明, HCOPSO算法获得的时间加权绝对误差积分(ITAE)指标较PSO、GA、WOA等算法分别降低了55.38%、22.47%和24.63%, 并表现出较强的扰动抑制能力与航向保持能力, 验证了其有效性。
- 无人船 /
- 航向控制 /
- 改进Smith预估器 /
- PID控制 /
- 时滞系统 /
- HCOPSO算法
Abstract: In the heading control of high-speed unmanned surface vessel(USV), the presence of time delay elements in both the forward channel and feedback loop significantly degrades the system's overall performance. Moreover, a larger delay to dynamic time ratio further exacerbates the control difficulty. Conventional Smith predictors can only effectively compensate for time delays in the forward channel and are ineffective against time delays in the feedback loop. In this paper, the time delay in the feedback loop is incorporated into the design of the Smith predictor, constructing a predictive model that accounts for time delays in both directions. This approach allows for simultaneous compensation of time delays in both the forward and feedback paths, thereby significantly reducing the erosion of the system's phase margin caused by bidirectional time delays. Furthermore, a hybrid mean center opposition based learning particle swarm optimization (HCOPSO) algorithm is introduced for the parameter tuning of the PID controller. This algorithm employs a mean center opposition - based learning strategy in the early stages of iteration to expand the search range and utilizes an adaptive compression factor in the later stages for fine-tuning. Thus, it combines the advantages of both global exploration and local exploitation. Simulation results based on a USV heading model demonstrate that the improved Smith predictor PID controller shows significant improvements in system overshoot and settling time compared to conventional PID controllers and traditional Smith predictor PID controllers, with a steady-state error of less than 0.1°. When the compensation model of the optimized Smith predictor contains parameter deviations, the system can still maintain good dynamic stability and steady-state accuracy. Additionally, when comparing the HCOPSO algorithm with other algorithms such as PSO, GA, and WOA for parameter optimization of the improved Smith predictor PID controller, the HCOPSO algorithm achieves an ITAE index that is respectively 55.38%, 22.47%, and 24.63% lower than those obtained by PSO, GA, and WOA, and it exhibits stronger disturbance suppression capability and faster heading recovery performance under different disturbance scenarios, which further verifies the effectiveness of the proposed method.
- unmanned surface vessel /
- heading control /
- optimized Smith predictor /
- PID Control /
- time-delay system /
- HCOPSO algorithm

HTML全文

图 1 USV闭环航向控制系统

Figure 1. Closed-loop heading control system of USV

下载: 全尺寸图片幻灯片

图 2 闭环航向控制系统

Figure 2. Closed-loop heading control system

下载: 全尺寸图片幻灯片

图 3 引入传统Smith预估器的闭环航向控制系统

Figure 3. Closed-loop heading control system with traditional Smith predictor

下载: 全尺寸图片幻灯片

图 4 引入传统Smith预估器的等效闭环航向控制系统

Figure 4. Equivalent closed-loop heading control system with traditional Smith predictor

下载: 全尺寸图片幻灯片

图 5 引入改进Smith预估器的闭环航向控制系统

Figure 5. Closed-loop heading control system with optimized Smith predictor

下载: 全尺寸图片幻灯片

图 6 引入改进Smith预估器的闭环航向控制等效系统

Figure 6. Equivalent closed-loop heading control system with optimized Smith predictor

下载: 全尺寸图片幻灯片

图 7 PID控制框图

Figure 7. The Control Block Diagram of PID

下载: 全尺寸图片幻灯片

图 8 HCOPSO算法优化控制器参数的过程

Figure 8. Process of optimizing parameters of controller using HCOPSO algorithm

下载: 全尺寸图片幻灯片

图 9 改进Smith预估PID控制器的USV闭环系统仿真模型

Figure 9. Simulation Model of Closed-loop System with Optimized Smith Predictor based PID Controller of USV

下载: 全尺寸图片幻灯片

图 10 单阶跃输入下的改进Smith控制对航向角控制效果的对比验证

Figure 10. Comparison and verification of the control effect of optimized smith control on heading angle under single step input

下载: 全尺寸图片幻灯片

图 11 不同阶跃输入下的改进Smith控制对航向角控制效果的对比验证

Figure 11. Comparison and verification of the control effect of optimized smith control on heading angle under different step input

下载: 全尺寸图片幻灯片

图 12 阶跃输入下不同系统的舵角输出曲线对比图

Figure 12. Comparison of Rudder Angle Output Curves of Different Systems under Step Input

下载: 全尺寸图片幻灯片

图 13 补偿模型存在偏差时系统的航向角曲线图

Figure 13. Heading angle curves of the system with deviation in the compensation model

下载: 全尺寸图片幻灯片

图 14 不同算法的适应度收敛曲线

Figure 14. Fitness convergence curves of different algorithms

下载: 全尺寸图片幻灯片

图 15 采用不同控制方法的USV航向角输出对比

Figure 15. The Comparison of the Heading Angle Output of the USV with Different Control Methods

下载: 全尺寸图片幻灯片

图 16 不同干扰下采用不同算法的USV航向角与舵角输出对比

Figure 16. comparison of the heading angle output and rudder angle output of the usv with different control methods under different prescribed disturbance

下载: 全尺寸图片幻灯片

表 1 HCOPSO算法的伪代码

Table 1. Pseudocode of the hybrid mean center reverse learning particle swarm optimization algorithm

算法: 混合均值中心反向学习粒子群优化(HCOPSO)算法
输入: 种群数N, 维度D, 惯性权重w, 学习因子c1, c2, 最大迭代Max_iter, 最大评估Max_eval, 边界[xmin, xmax]
输出: 全局最优位置g及其适应度f(g)
1. 随机初始化粒子位置x_i和速度v_i, i=1 to N; p_i=x_i
2. 计算f(x_i), 若f(x_i)更优则更新个体最优p_i; 设置全局最优g
3. for iter = 1 to Max_iter do
4.　for i = 1 to N do
5.　　for d = 1 to D do
6.　　　v_i[d] = w * v_i[d] + c1 * r1 * (p_i[d] − x_i[d]) + c2 * r2 * (g[d] − x_i[d])
7.　　　x_i[d] = x_i[d] + v_i[d]
8.　　　if f(x_i)更优于f(p_i) then p_i=x_i
9.　　　if f(x_i)更优于f(g) then g=x_i
10.　　end for
11.　end for
12.　计算x_MC, x_PMC, x_HMC(依次由式(11), 式(12), 式(13)可得)
13.　计算x_OBL_HMC(由式(14)可得)
14.　if f(x_OBL_HMC)更优于f(g) then g=x_OBL_HMC
15.　if eval ≥ Max_eval then break
16. end for
17. return g, f(g)

下载: 导出CSV

表 2 基于改进Smith预估PID控制器的控制系统框架下不同算法最佳适应度值

Table 2. Optimal fitness values of different algorithms under the control system framework of optimized smith predictor PID controller

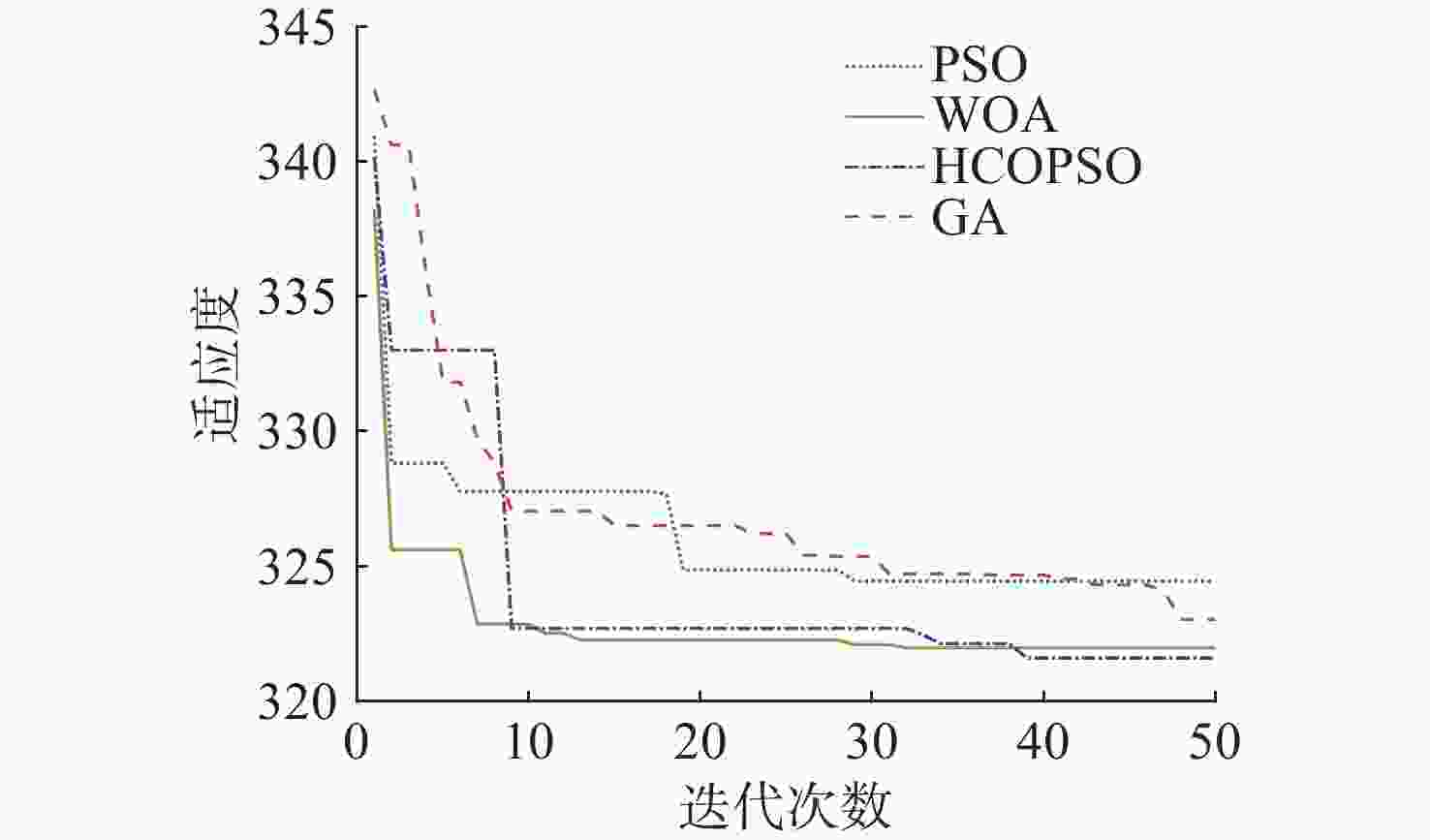
智能优化算法	$ {K_{\text{P}}} $	$ {K_{\text{I}}} $	$ {K_{\text{D}}} $	迭代次数	最佳适应度值
PSO	3.34	0	5.00	29	324.4
WOA	6.61	0	15.11	32	322.0
HCOPSO	4.13	0	10.21	39	321.6
GA	3.77	0.000 2	8.75	48	323.0

下载: 导出CSV

表 3 不同算法整定的PID参数值和动态响应指标

Table 3. The PID Parameter Values and Dynamic Response Indices Tuned by Different GAAlgorithms

智能优化算法	超调量/%	调节时间/s	ITAE	峰值时间/s
PSO	46.3	71.4	8 341	43.0
WOA	32.0	57.9	4 801	42.0
HCOPSO	20.4	52.0	3 722	41.0
GA	31.4	58.1	4 938	42.0

下载: 导出CSV

参考文献(27)

[1]	TOUZOUT W, BENMOUSSA Y, BENAZZOUZ D, et al. Unmanned surface vehicle energy consumption modelling under various realistic disturbances integrated into simulation environment[J]. Ocean Engineering, 2021, 222: 108560. doi: 10.1016/j.oceaneng.2020.108560
[2]	祝川, 卢俊, 吴翔. 无人艇直驱式电液伺服舵机系统建模与仿真[J]. 舰船科学技术, 2019, 41(23): 87-92. ZHU C, LU J, WU X. Modeling and simulation of direct-drive electro-hydraulic servo steering-gear system of USV[J]. Ship Science and Technology, 2019, 41(23): 87-92.
[3]	GE Y, ZHONG L, QIANG Z J. Research on USV heading control method based on Kalman filter sliding mode control[C]//Proceedings of the 32nd 2020 Chinese Control and Decision Conference. Hefei, China: IEEE, 2020: 1547-1551.
[4]	周嘉俊, 吴萌岭, 刘宇康, 等. 基于改进史密斯预估器的列车制动减速度控制研究[J]. 同济大学学报(自然科学版), 2020, 48(11): 1657-1667. ZHOU J J, WU M L, LIU Y K, et al. Train braking deceleration control based on improved smith estimator[J]. Journal of Tongji University(Natural Science), 2020, 48(11): 1657-1667.
[5]	Al-Dhaifallah M. Fractional order and smith predictor structure—performance analysis for pressure control process[C]//Proceedings of the 2023 20th International Multi-Conference on Systems, Signals & Devices(SSD). Mahdia, Tunisia: IEEE, 2023: 700-704.
[6]	DING Q H, FANG B. Research on the application of improved smith predictor on control systems which contain time-delay in feedback path[C]//Proceedings of the 32nd Chinese Control Conference. Xi’an, China: IEEE, 2017: 309-312.
[7]	MEHALLEL A, FELIU-BATLLE V. Reducing the impacts of withdrawals on the water distribution in main irrigation canals based on a modified smith predictor control scheme[J]. Water, 2025, 17(3): 373.
[8]	王健, 祖广浩. 磁流变半主动悬架的史密斯预估-LQG时滞补偿控制方法[J]. 重庆理工大学学报(自然科学), 2017, 31(8): 65-72,80. WANG J, ZU G H. Smith predictor-LQG control for time delay compensation of magneto-rheological semi-active suspension[J]. Journal of Chongqing University of Technology(Natural Science), 2017, 31(8): 65-72,80.
[9]	INYANG I J, WHIDBORNE J F. Applying a modified Smith predictor–bilinear proportional plus integral control for directional drilling[J]. IFAC-PapersOnLine, 2017, 50(2): 139-144. doi: 10.1016/j.ifacol.2017.12.026
[10]	SINGHA P, MEENA R, CHAKRABORTY S, et al. Robust PIDF-PID cascade control scheme for delay-dominant stable and integrating chemical processes[J]. Journal of the Taiwan Institute of Chemical Engineers, 2025, 173: 106165. doi: 10.1016/j.jtice.2025.106165
[11]	苗河泉, 刁培松, 徐广飞, 等. 基于改进史密斯预估控制的电液转向时滞补偿研究[J]. 农机化研究, 2023, 45(7): 232-237. MIAO H Q, DIAO P S, XU G F, et al. Research on time-delay compensation of electro-hydraulic steering based on improved smith predictor control[J]. Journal of Agricultural Mechanization Research, 2023, 45(7): 232-237.
[12]	MORALES L. Smith predictor based LAMDA sliding-mode control applied to a mixing tank with variable dead time[C]//2022 IEEE ANDESCON. Barranquilla, Colombia: IEEE, 2022: 1-6.
[13]	TANG G, LEI J M, DU H H, et al. Proportional-integral-derivative controller optimization by particle swarm optimization and back propagation neural network for a parallel stabilized platform in marine operations[J]. Journal of Ocean Engineering and Science, 2025, 10(1): 1-10.
[14]	FU J, GU S, WU L, et al. Research on optimization of diesel engine speed control based on UKF-Filtered data and PSO fuzzy PID control[J]. Processes, 2025, 13(3): 777. doi: 10.3390/pr13030777
[15]	ALI Z M, AHMED A M, HASANIEN H M, et al. Optimal design of fractional-order PID controllers for a nonlinear AWS wave energy converter using hybrid jellyfish search and particle swarm optimization[J]. Fractal and Fractional, 2024, 8(1): 6.
[16]	GHADIMI N. A new hybrid algorithm based on optimal fuzzy controller in multimachine power system[J]. Complexity, 2013, 21(1): 78-93.
[17]	LI B, CHE X Q, LIU C Y, et al. Parameter optimization of unmanned surface vessel propulsion motor based on BAS-PSO[J]. International Journal of Advanced Robotic Systems, 2022, 19(2): 172988142110406.
[18]	ZHANG H X, ZHAO Z, WEI Y C, et al. A self-tuning variable universe fuzzy PID control framework with hybrid BAS-PSO-SA optimization for unmanned surface vehicles[J]. Journal of Marine Science and Engineering, 2025, 13(3): 558.
[19]	陈明志, 刘兰军, 陈家林, 等. 基于HCOPSO算法的USV舵向PID控制参数整定方法[J]. 水下无人系统学报, 2023, 31(3): 381-387. CHEN M Z, LIU L J, CHEN J L, et al. Parameter tuning method for USV rudder steering PID control based on HCOPSO algorithm[J]. Journal of Unmanned Undersea Systems, 2023, 31(3): 381-387.
[20]	ZHAO S Q, MU J R, LIU H D, et al. Heading control of USV based on fractional-order model predictive control[J]. Ocean Engineering, 2025, 322: 120476. doi: 10.1016/j.oceaneng.2025.120476
[21]	MCCUE L. Handbook of marine craft hydrodynamics and motion control[J]. IEEE Control Systems, 2016, 36(1): 78-79. doi: 10.1109/MCS.2015.2495095
[22]	韩巍, 高丙坤, 郭浩轩. 分数阶时滞系统的Smith预估分数阶PI控制[J]. 吉林大学学报(信息科学版), 2020, 38(5): 542-547. HAN W, GAO B K, GUO H X. Smith predictor fractional order PI control for fractional order with time delay[J]. Journal of Jilin University(Information Science Edition), 2020, 38(5): 542-547.
[23]	孙辉, 邓志诚, 赵嘉, 等. 混合均值中心反向学习粒子群优化算法[J]. 电子学报, 2019, 47(9): 1809-1818. SUN H, DENG Z C, ZHAO J, et al. Hybrid mean center opposition-based learning particle swarm optimization[J]. Acta Electronica Sinica, 2019, 47(9): 1809-1818.
[24]	朱蓉, 靳雁霞, 范卫华. 融合优质粒子分布的粒子群优化算法[J]. 小型微型计算机系统, 2015, 36(3): 576-580. ZHU R, JIN Y X, FAN W H. Particle swarm optimization algorithm combination with the distribution of superior quality particles[J]. Journal of Chinese Computer Systems, 2015, 36(3): 576-580.
[25]	TIZHOOSH H R. Opposition-based learning: A new scheme for machine intelligence[C]//International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. Vienna, Austria: IEEE, 2005: 695-701.
[26]	MA X L, LIU F, QI Y T, et al. MOEA/D with opposition-based learning for multiobjective optimization problem[J]. Neurocomputing, 2014, 146: 48-64.
[27]	姜继海, 苏文海, 张洪波, 等. 直驱式容积控制电液伺服系统及其在船舶舵机上的应用[J]. 中国造船, 2004, 45(4): 58-63. JIANG J H, SU W H, ZHANG H B, et al. Direct drive volume control of electro-hydraulic servo system and its application to the steering system of ship[J]. Shipbuilding of China, 2004, 45(4): 58-63.