Numerical Simulation Study on Release Process of Underwater Towed Bodies under Different Parameters
-
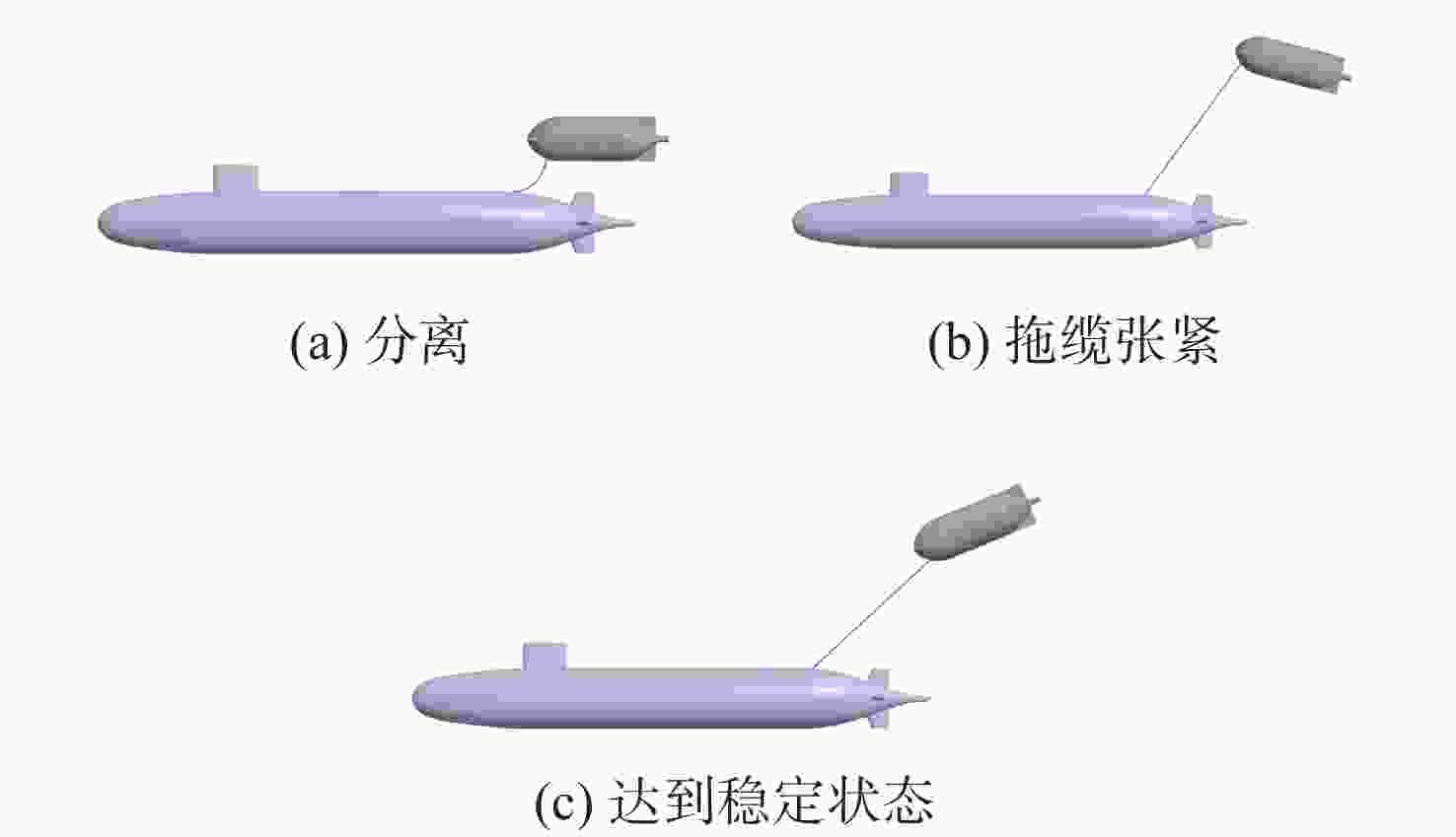
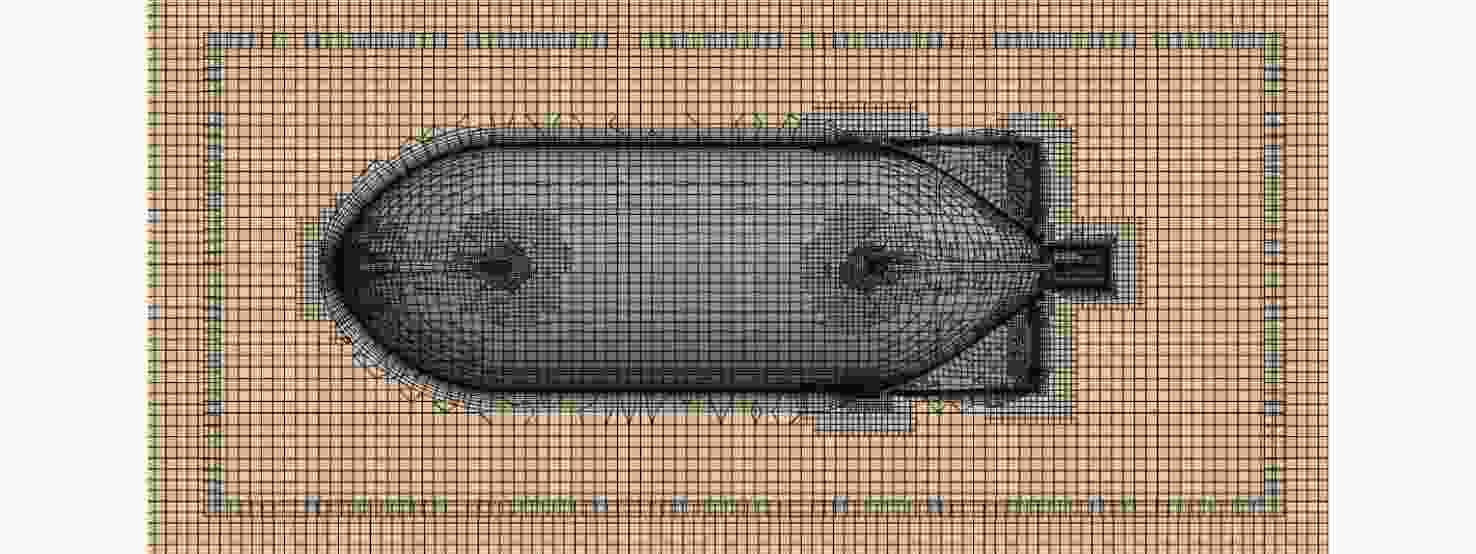
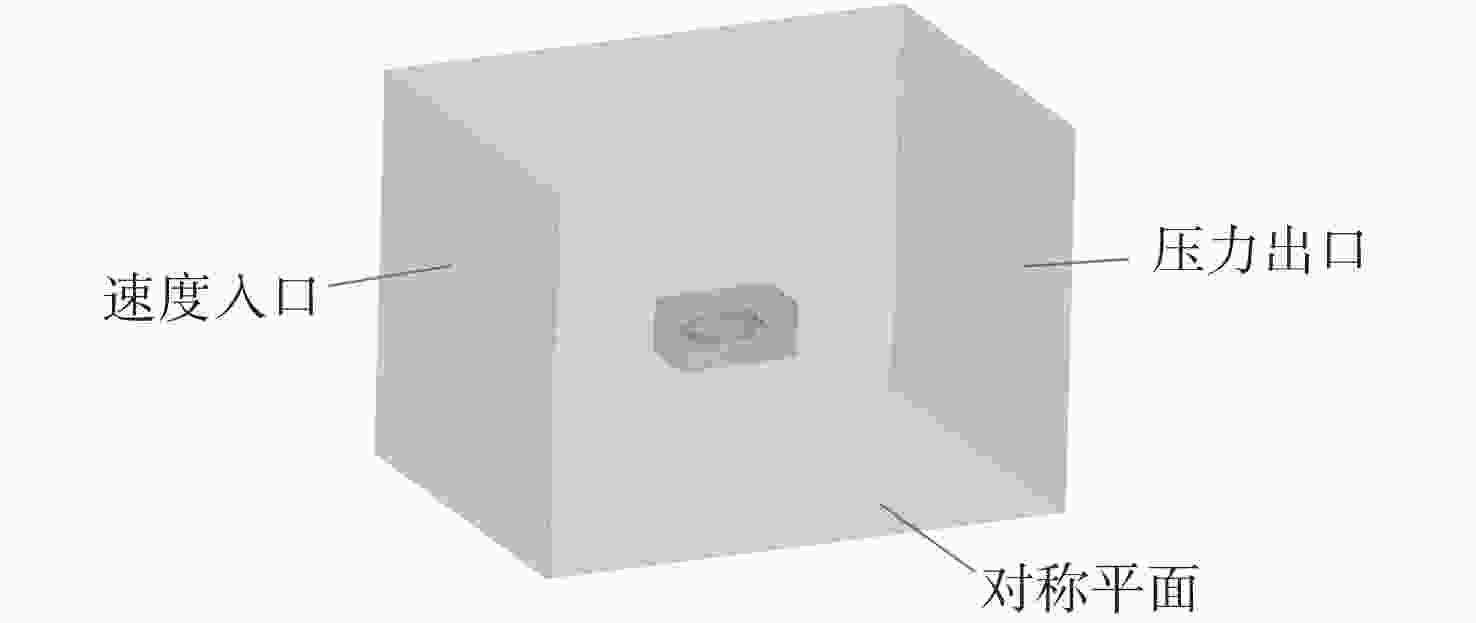
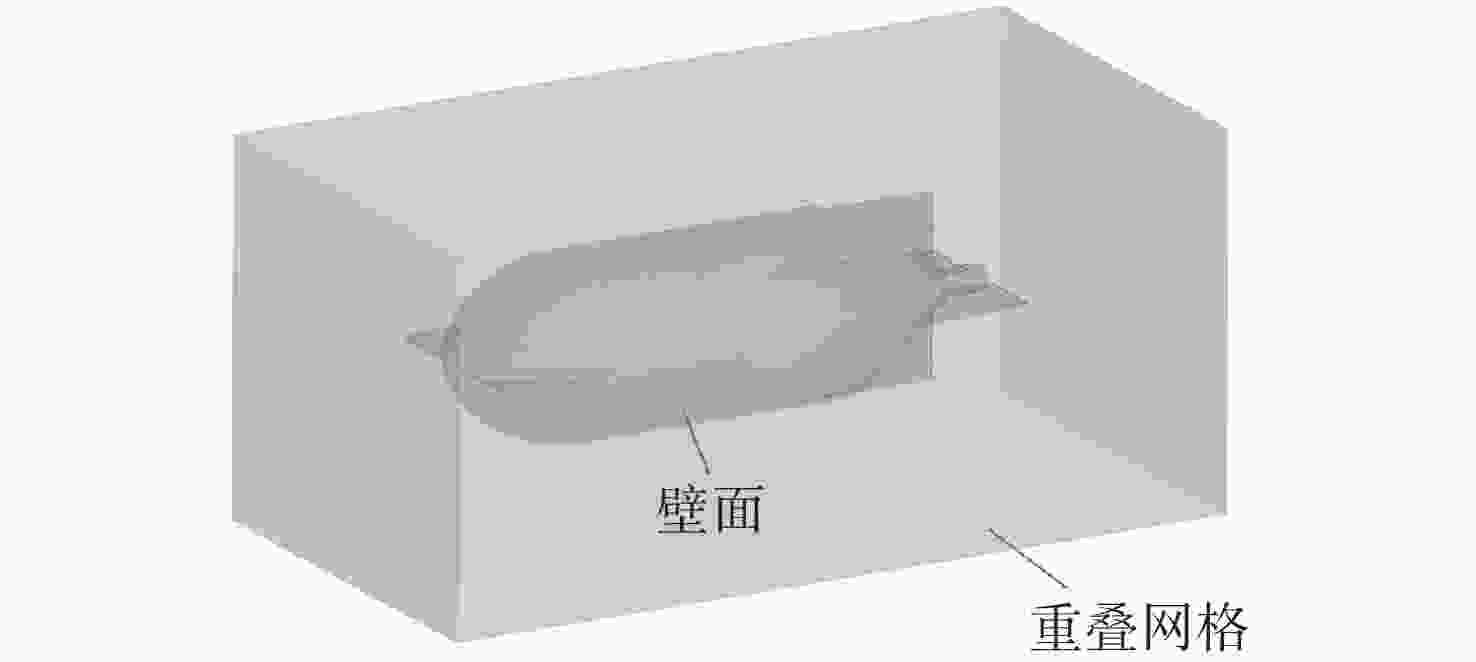
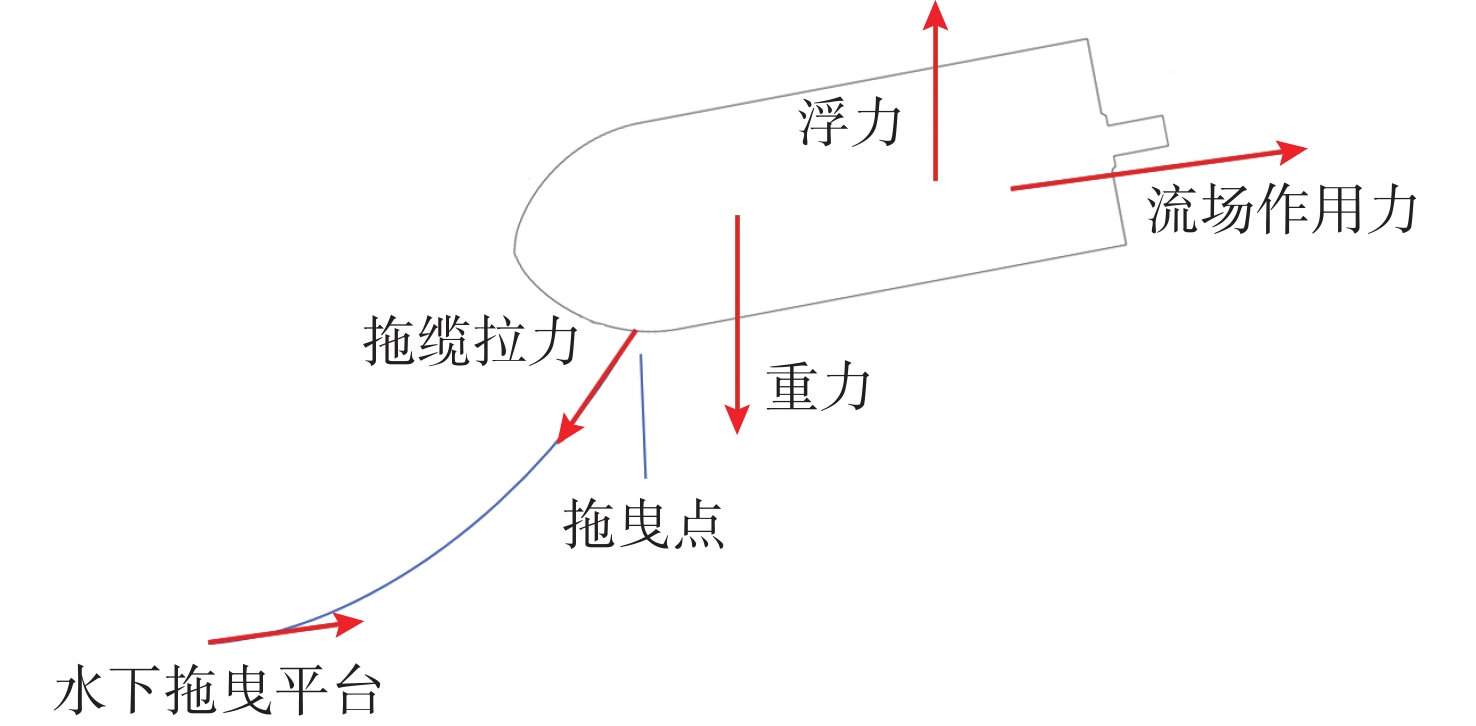
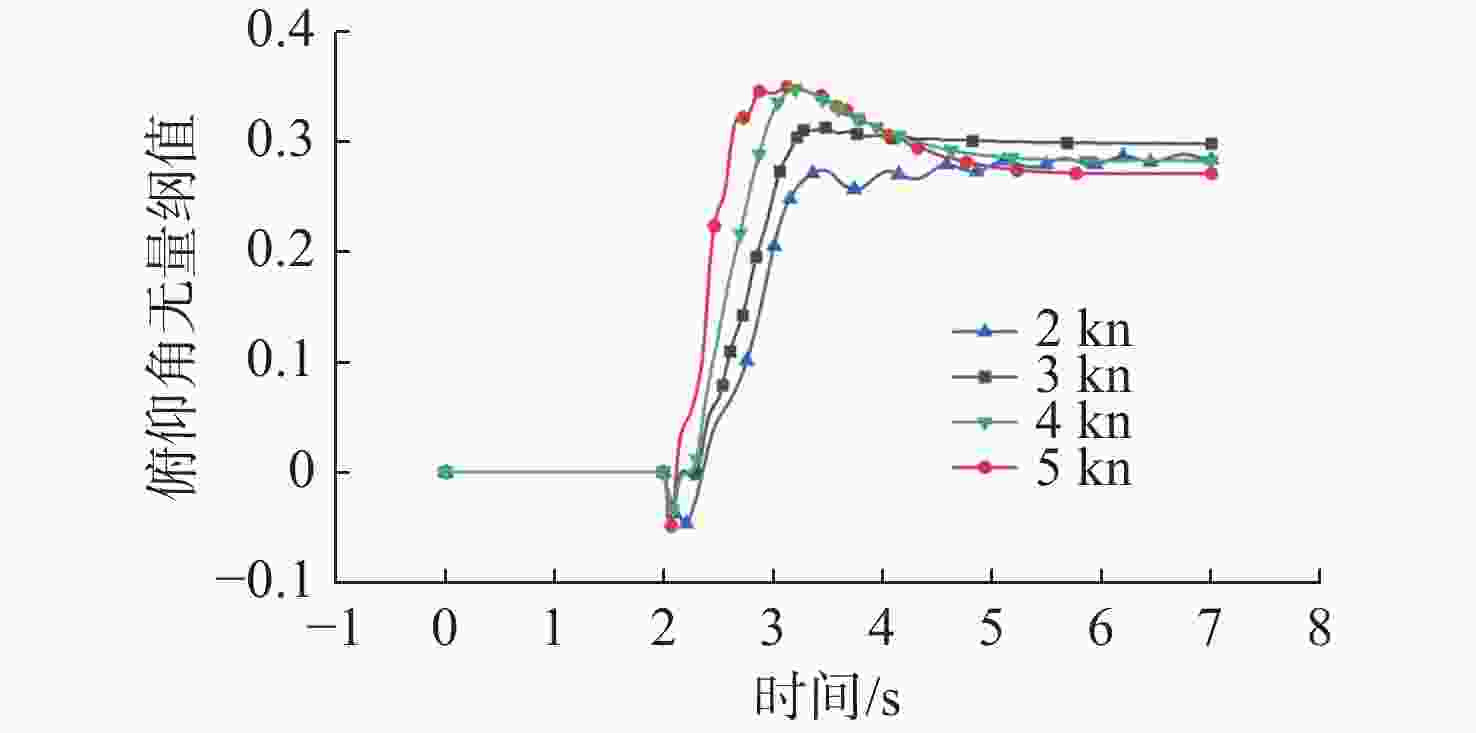
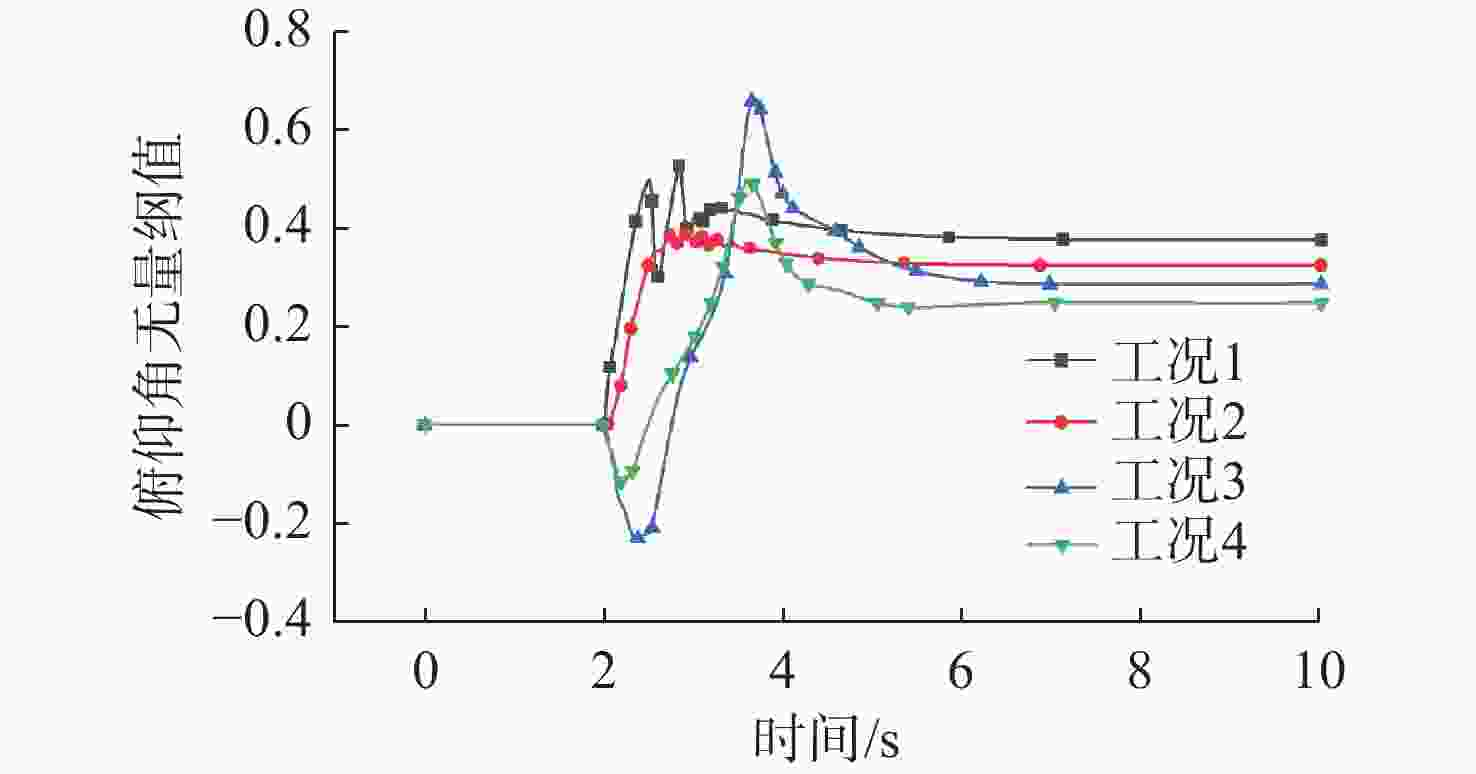
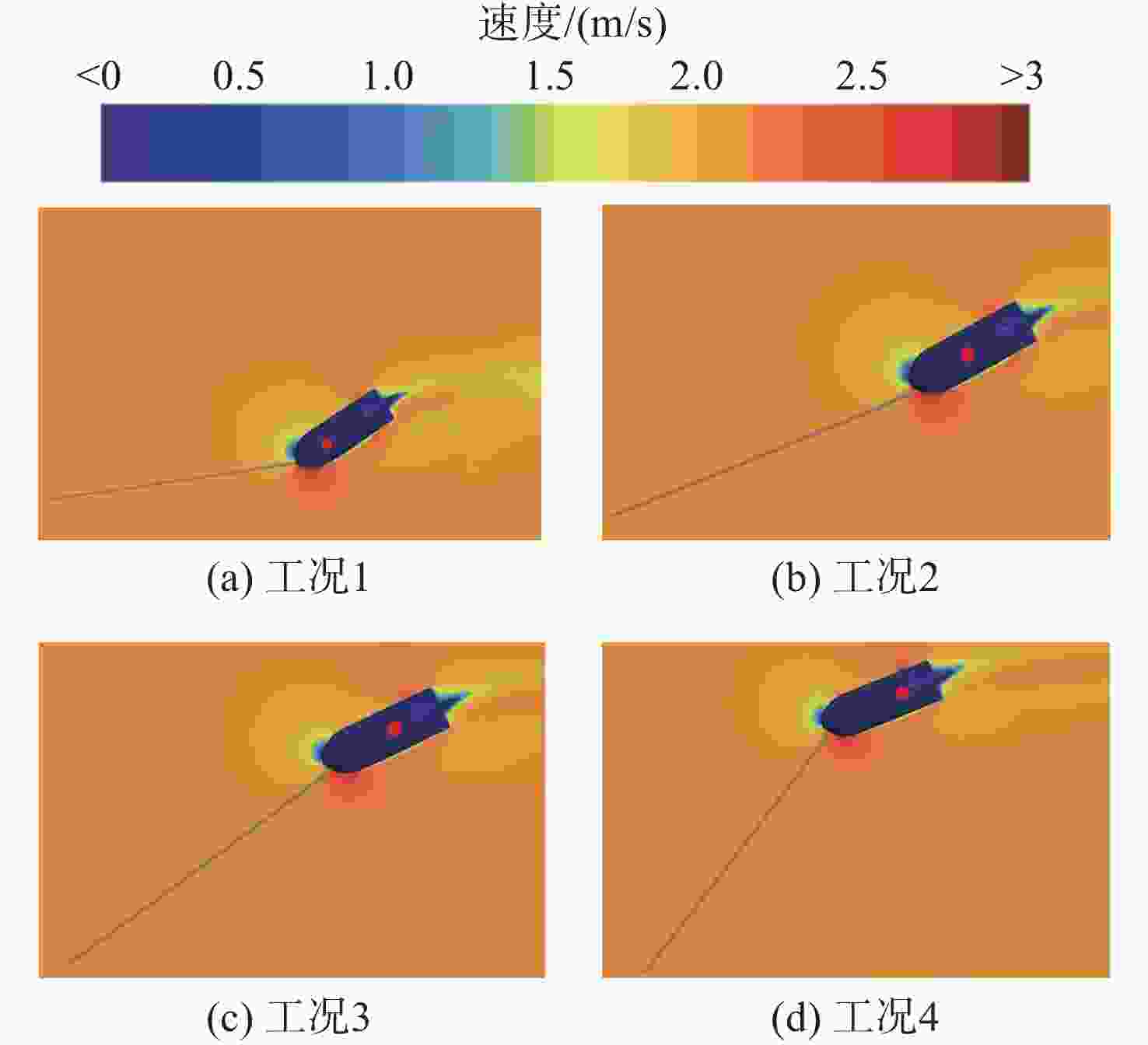
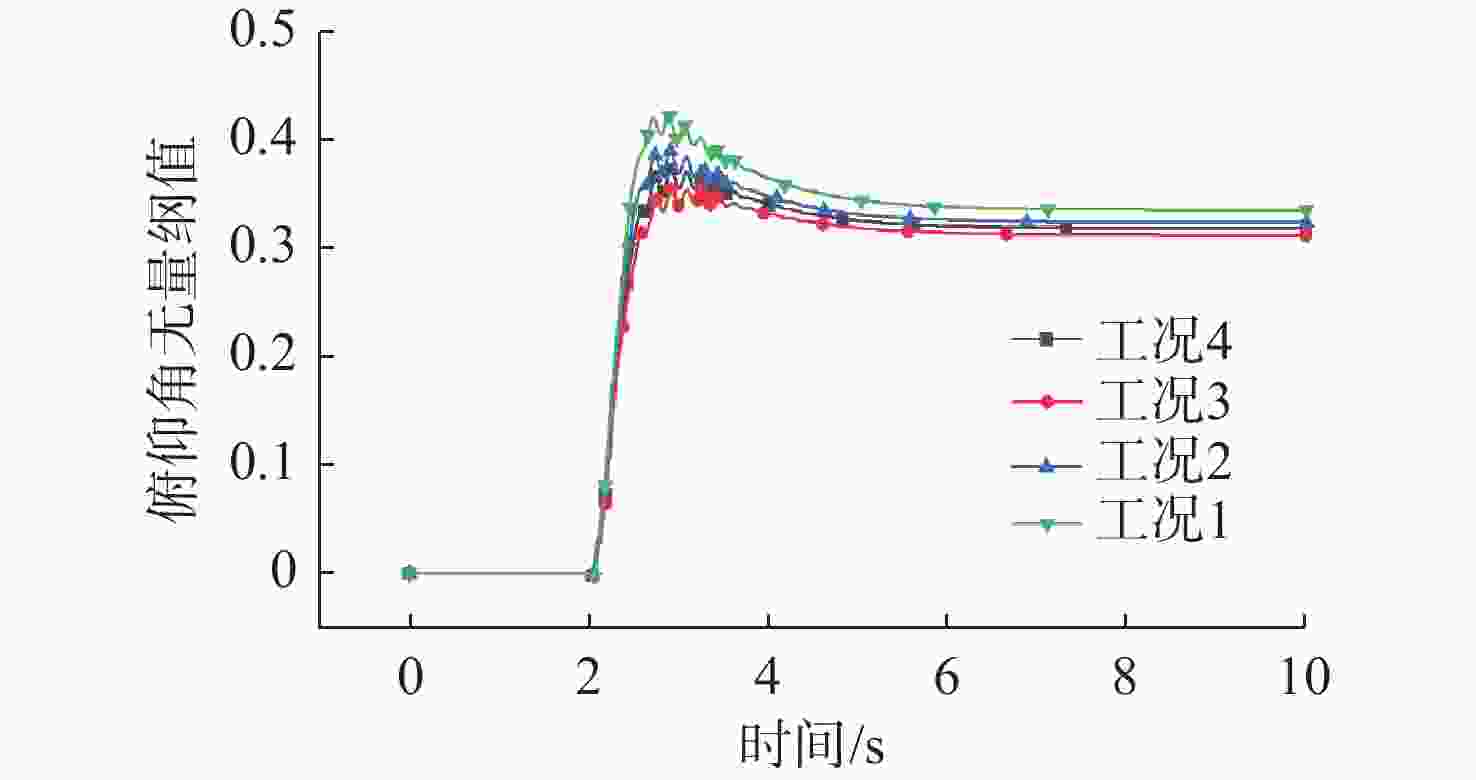
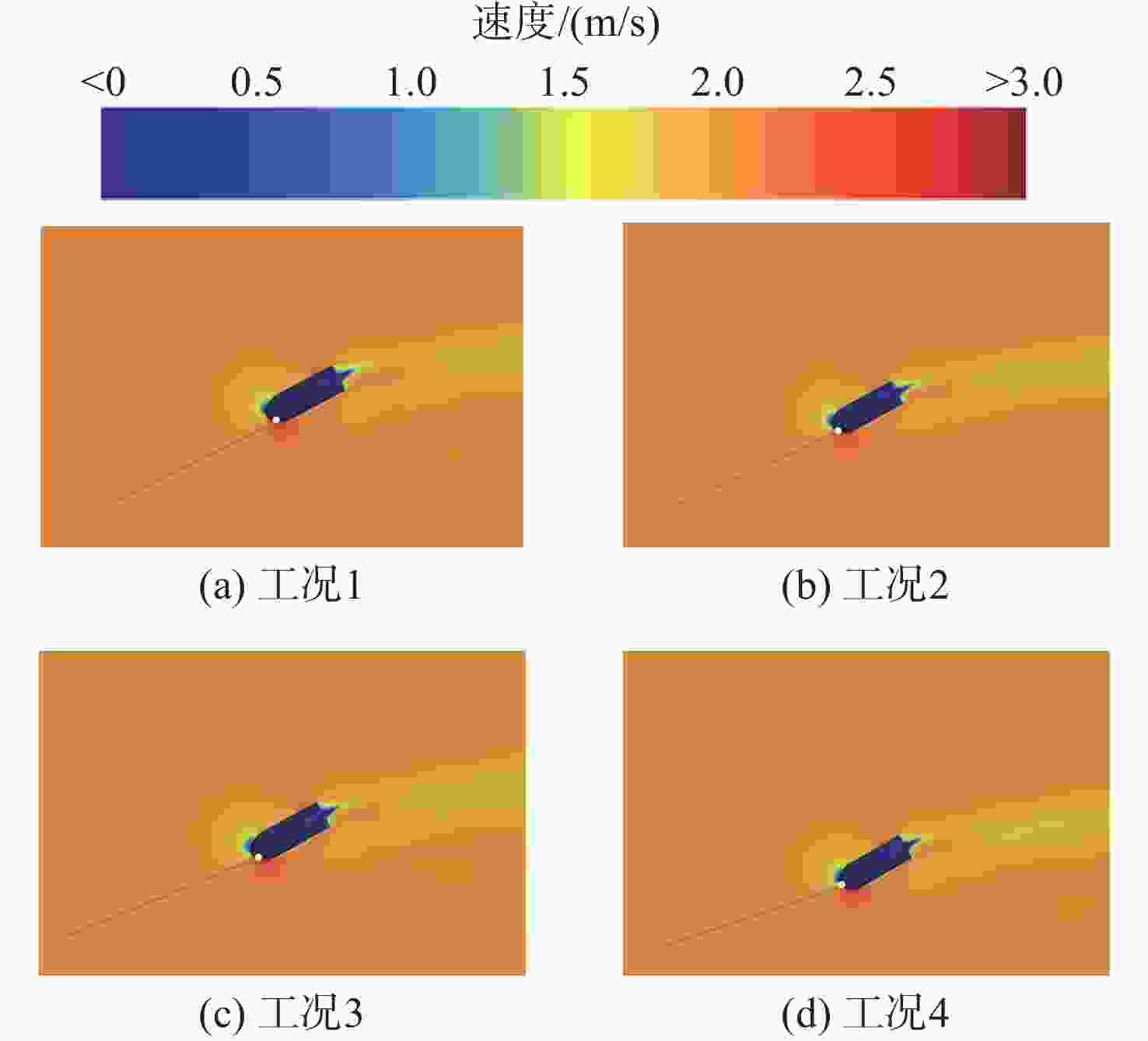
摘要: 水下拖曳体是水下航行器的重要部件, 为满足其拖缆设计及释放过程中姿态稳定的需求, 文中开展了相关研究。首先, 采用重叠网格技术与可实现的k-ε湍流模型, 构建拖曳体流体动力学模型, 并对其释放过程进行非定常数值仿真; 随后, 通过试验结果验证了网格划分与数值方法的有效性。在此基础上进一步系统分析了拖曳速度、重浮心位置以及拖曳点位置三大关键因素对水下拖曳体释放过程的影响规律, 仿真结果表明: 拖曳速度影响拖曳体的稳定时间与姿态稳定过程, 需根据拖曳体结构确定最佳拖曳速度; 重浮心位置对拖曳体释放动力学特性作用显著, 重心前移设计可减小拖曳体振荡、提升系统稳定性, 且重心与浮心接近时, 拖曳体姿态调整时间更短、运动更平稳; 拖曳点应选在拖曳体头部下方, 以减小释放过程中俯仰角的变化、提高释放稳定性。研究结果为水下拖曳体的工程设计与释放策略提供了重要理论依据。Abstract: The underwater towed body is an important component of underwater vehicles. For the requirements such as the design of the towing cable for underwater towed bodies and stable attitude during the release process, this paper constructed the fluid dynamics model of the towed body by the overlapping mesh technology and the achievable k-ε turbulence model. It also carried out the unsteady numerical simulation of the release process. After the simulation, the paper verified the effectiveness of the grid division and numerical methods through the experimental results. The paper systematically analyzed the influence of towing speed, the position of the barycenter and the buoyant center, and the towing point on the release process of the underwater towed body. The simulation results show that towing speed affects the stabilization time and attitude stabilization process of the towed body, and the optimal towing speed needs to be determined according to the structure of the towed body. The positions of the barycenter and the buoyant center have a significant effect on the release dynamic characteristics of the towed body, and the design of moving the barycenter forward can reduce the oscillation of the towed body and improve the stability of the system. When the barycenter is close to the buoyant center, the attitude adjustment time of the towed body is shorter, and the movement is more stable. The towing point should be under the head of the towed body to reduce the change in pitch angle during the release process and improve the stability of the release process. The results provide an important theoretical basis for the engineering design and release strategy of underwater towed bodies.
-
Key words:
- underwater vehicle /
- towed body /
- release process /
- overlapping grid
-
表 1 拖曳体结构参数
Table 1. Structural parameters of towed body
参数/单位 数值 质量/kg 6.928 总长度/mm 540 中段直径/mm 170 x方向浮心位置/m 0.243 8 y方向浮心位置/m 0 z方向浮心位置/m 0 x方向转动惯量/(kg/m2) 0.028 435 y方向转动惯量/(kg/m2) 0.107 598 z方向转动惯量/(kg/m2) 0.106 637 表 2 不同网格数量下拖曳体稳态阻力与升力大小
Table 2. The steady-state resistance and lift force of the towing body under different grid numbers
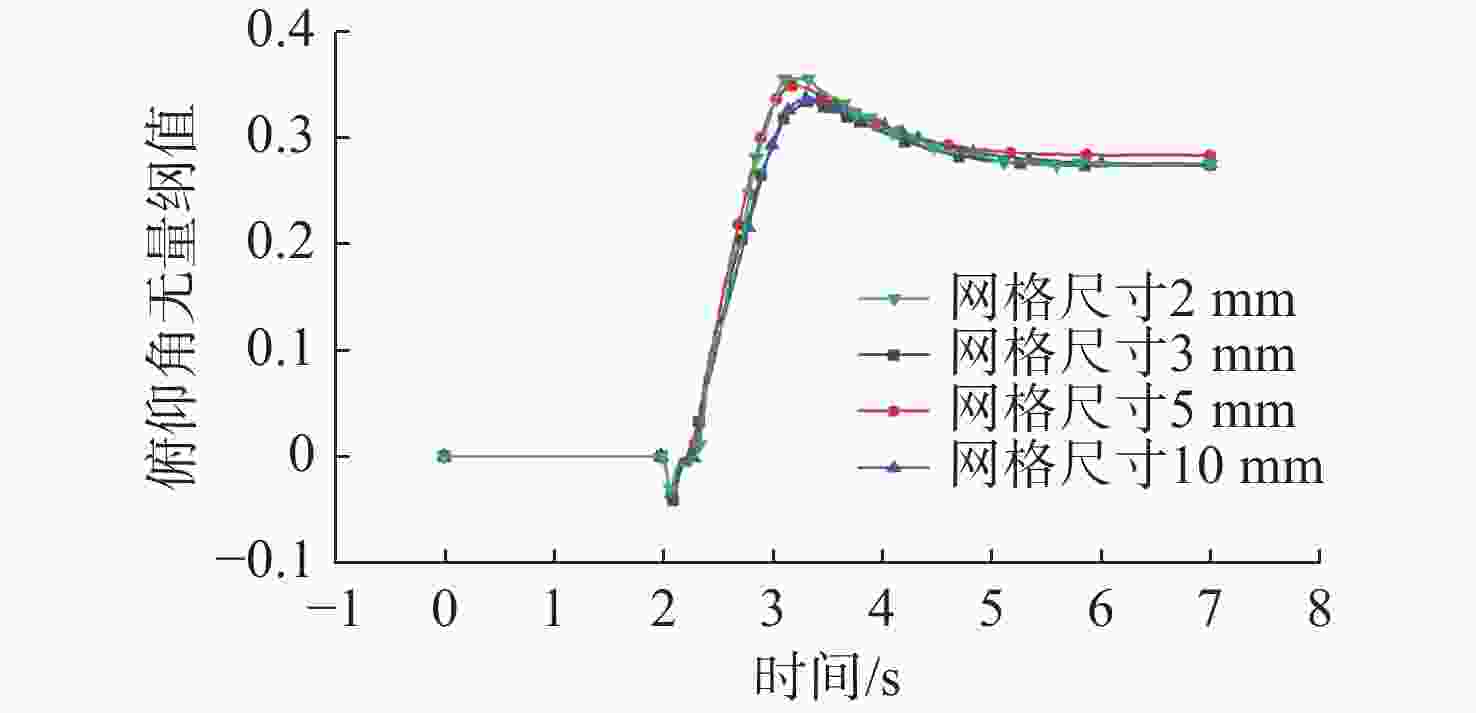
表面网格尺寸/mm 网格总数 水平阻力/N 竖直升力/N 10 188 975 33.77 21.36 5 283 445 34.21 21.19 3 986 964 32.79 22.00 2 1 902 176 32.96 21.84 表 3 4 kn航速下拖曳体俯仰角数值仿真误差
Table 3. Numerical simulation errors of the pitch angle of the towed body at a speed of 4 kn
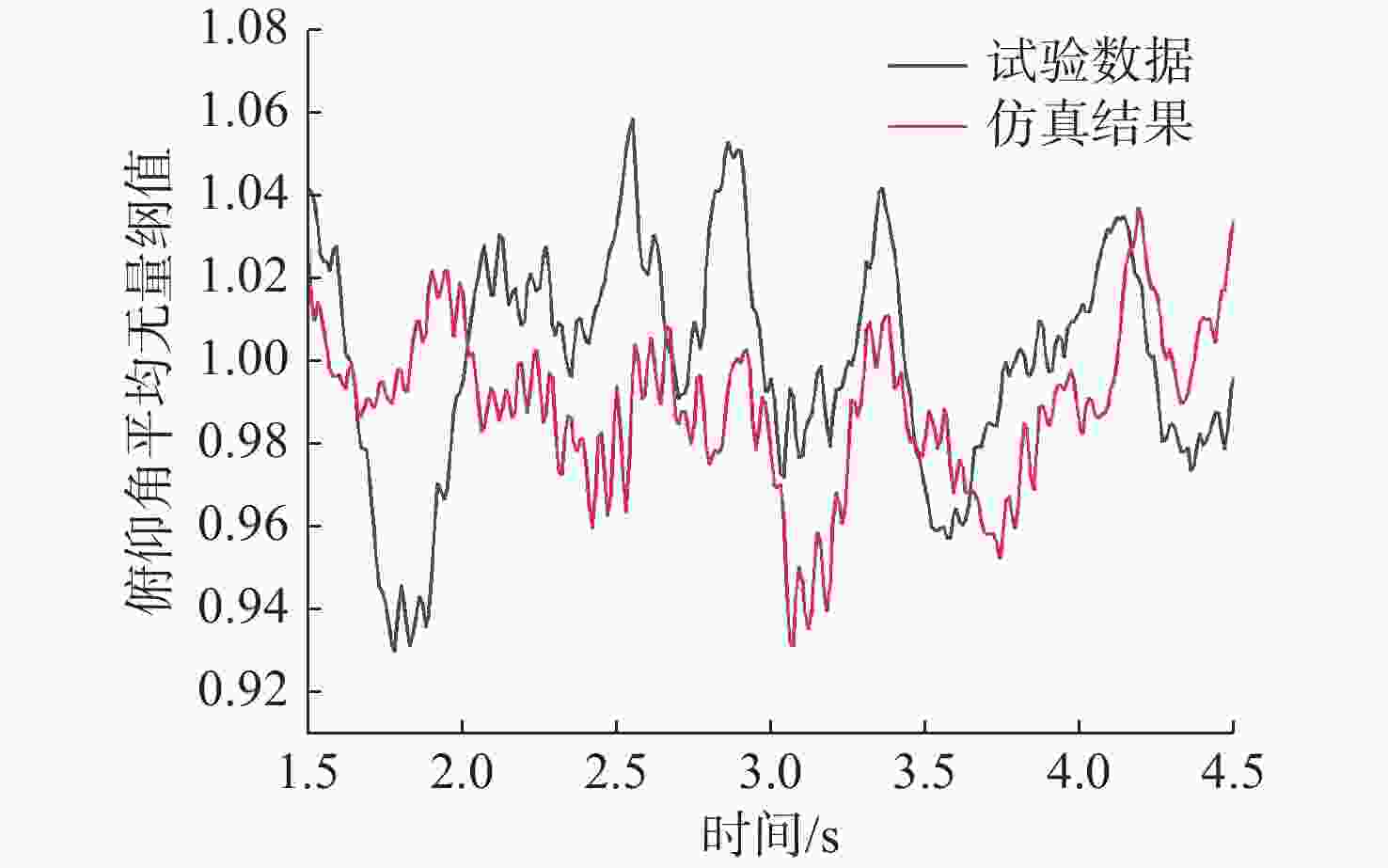
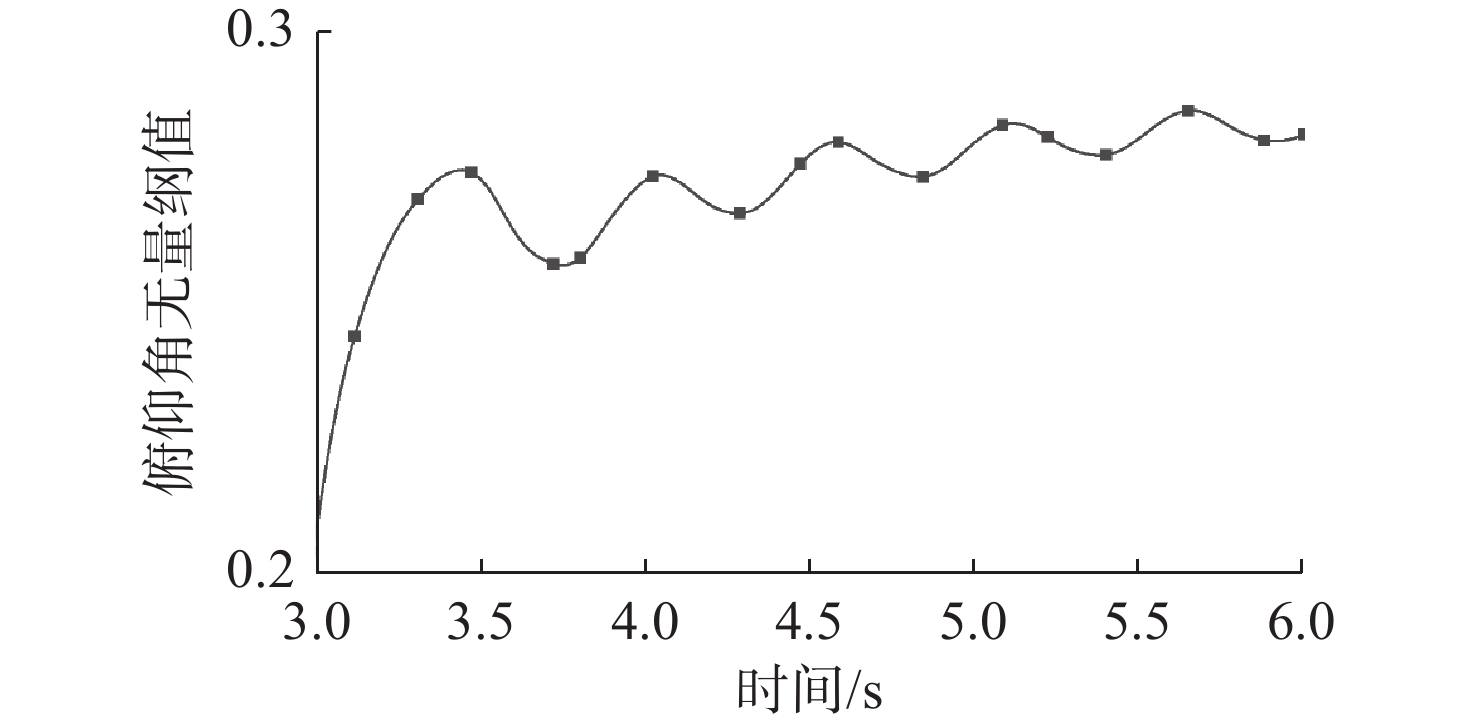
名称 仿真结果 试验数据 误差/% 平均值 56.558 59.188 4.44 中位数 56.420 59.156 4.63 表 4 改变重心位置的不同工况参数
Table 4. Different operating condition parameters for varying the center of gravity position
工况 重心横坐标/m $\Delta X/L$ 备注 1 0.043 8 0.08 重心位于浮心前方 2 −0.006 2 −0.01 重心与浮心基本重合 3 −0.056 2 −0.10 重心位于浮心后方 4 −0.106 2 −0.29 重心位于浮心后方, 且间距更大 表 5 改变拖曳点位置的不同工况参数
Table 5. Different working condition parameters with changed towing point positions
工况 拖曳点横坐标/m $\alpha $/(°) 1 0.231 8 30.82 2 0.218 8 45.10 3 0.201 8 59.61 4 0.191 8 67.16 -
[1] 张巍. 对潜通信技术的发展动向与分析[J]. 舰船电子工程, 2016, 36(6): 13-16, 41.ZHANG W. Development trend and analysis of submarine communication technology[J]. Ship Electronic Engineering, 2016, 36(6): 13-16, 41. [2] 杨坤, 杜度. 国外对潜通信技术发展研究[J]. 舰船科学技术, 2018, 40(2): 153-157.YANG K, DU D. Research on the development of foreign submarine communication technology[J]. Ship Science and Technology, 2018, 40(2): 153-157. [3] 王帅, 孟旭东, 陈小星. 拖体水动力特性的流体力学分析[J]. 机电工程技术, 2024, 53(1): 163-170.WANG S, MENG X D, CHEN X X. Hydromechanical analysis of towed body on hydrodynamic characteristics[J]. Mechanical & Electrical Engineering Technology, 2024, 53(1): 163-170. [4] ABKOWITZ M A. Stability and motion of ocean vehicles[M]. Cambridge: MIT Press, 1969: 32-50. [5] LANDSTAD O, HALVORSEN H S, ØVERAAS H, et al. Dynamic positioning of ROV in the wave zone during launch and recovery from a small surface vessel[J]. Ocean Engineering, 2021, 235: 109382. [6] 吴方良, 吴晓光, 许建. 潜艇主艇体三维粘性流场数值计算方法研究[J]. 中国造船, 2009, 50(2): 12-22.WU F L, WU X G, XU J. Method of numerical calculation of the 3D viscous flow field over a submarine main hull[J]. Shipbuilding of China, 2009, 50(2): 12-22. [7] 杨壮滔, 张镇, 何文生, 等. 水下无人平台动态布放UUV过程水动力特性[J]. 水下无人系统学报, 2022, 30(1): 115-121.YANG Z T, ZHANG Z, HE W S. Hydrodynamic characteristics of UUV during dynamic deployment process of underwater unmanned platform[J]. Journal of Unmanned Undersea Systems, 2022, 30(1): 115-121. [8] 张海亭. 面向USV自主回收AUV的拖曳装置研究[M]. 沈阳: 东北大学, 2018. [9] 高东勇. 基于无人艇AUV布放回收装置设计及拖曳动力学研究[D]. 沈阳: 沈阳工业大学, 2022. [10] LIU J, GAO S, NIAN R, et al. Study on hydrodynamic characteristics and depth control of the towed sensors array system[J]. Marine Structures, 2023, 92: 103504. doi: 10.1016/j.marstruc.2023.103504 [11] 马文宾, 向祖权, 茅云生. 船舶拖曳潜体回转和收放作业仿真[J]. 中国舰船研究, 2015, 10(5): 34-40.MA W B, XIANG Z Q, MAO Y S. Simulation of the towed body under turning and retraction[J]. Chinese Journal of Ship Research, 2015, 10(5): 34-40. [12] 马峥, 黄少锋, 朱德祥. 湍流模型在船舶计算流体力学中的适用性研究[J]. 水动力学研究与进展, 2009, 24(2): 207-216.MA Z, HUANG S F, ZHU D X. Study on applicability of turbulence model in ship computational fluid dynamics[J]. Chinese Journal of Hydrodynamics, 2009, 24(2): 207-216. [13] 谢楠, 郜焕秋. 浮标-缆-物体综合系统动力学二维时域分析[J]. 水动力学研究与进展, 2000, 15(2): 202-213.XIE N, GAO H Q. Two-dimensional time domain dynamic analysis for the general buoy-cable-body system[J]. Journal of Hydrodynamics, 2000, 15(2): 202-213. [14] SHIH T H, LIOU W W, SHABBIR A, et al. A new k-ε eddy viscosity model for high reynolds number turbulent flows[J]. Computers Fluids, 1995, 24(3): 227-238. [15] 孙辰, 陈志平, 宁春林, 等. 海洋资料浮标结构关键问题研究[J]. 杭州电子科技大学学报, 2013, 33(6): 146-149.SUN C, CHEN Z P, NING C L, et al. Research on key problems of ocean data buoy[J]. Journal of Hangzhou Dianzi University, 2013, 33(6): 146-149. [16] WALTON T S, POLACHEK H. Calculation of transient motion of submerged cables[J]. Mathematics of Computation, 1960, 14(69): 27-46. [17] 杜晓旭, 张小链. 拖缆对水下航行器的操纵性能影响[J]. 兵工学报, 2019, 40(7): 1476-1484.DU X X, ZHANG X L. Influence of towed cable on maneuverability of underwater vehicle[J]. Acta Armamentarii, 2019, 40(7): 1476-1484. [18] 苑志江, 金良安, 田恒斗, 等. 海洋拖曳系统的水动力理论与控制技术研究综述[J]. 科学技术与工程, 2013, 13(2): 408-415, 420.YUAN Z J, JIN L A, TIAN H D, et al. Comments on the research of hydrodynamic and control technology of underwater towed system[J]. Science Technology and Engineering, 2013, 13(2): 408-415, 420. [19] 褚悦, 刘平安, 黄曦, 等. 不同航行条件下超空泡航行器出水过程数值计算[J]. 水下无人系统学报, 2024, 32(3): 496-506.CHU Y, LIU P A, HUANG X, et al. Numerical calculation of water exit process of supercavitating vehicles under different sailing conditions[J]. Journal of Unmanned Undersea Systems, 2024, 32(3): 496-506. [20] 杜小振, 郭东兴, 王文秀, 等. 基于重叠网格技术柔性旗帜与流体耦合运动数值模拟[J]. 科学技术与工程, 2025, 25(2): 473-483.DU X Z, GUO D X, WANG W X, et al. Numerical simulation of flexible flag-fluid coupled motion based on overlapping grid technique[J]. Science Technology and Engineering, 2025, 25(2): 473-483. -




 下载:
下载: