水下滑翔机声学适配结构优化设计与仿真

陈博文; 张林; 孙芹东; 于法军

doi:10.11993/j.issn.2096-3920.2025-0042

水下滑翔机声学适配结构优化设计与仿真

doi: 10.11993/j.issn.2096-3920.2025-0042

1.
哈尔滨工程大学青岛创新发展基地, 山东青岛, 266400
2.
海军潜艇学院, 山东青岛, 266199

基金项目: 国家自然科学基金项目(52442113); 国家重点研发计划项目(2021YFC2100900).

详细信息

作者简介:
陈博文(2000-), 男, 硕士, 主要研究方向为水下滑翔机声学适配结构

通讯作者:
张林(1980-), 男, 教授, 主要研究方向为水声环境效应技术.

中图分类号: TJ630.22; U662.29
计量
- 文章访问数: 52
- HTML全文浏览量: 21
- PDF下载量: 15
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-05
- 修回日期: 2025-03-28
- 录用日期: 2025-04-14
- 网络出版日期: 2025-07-28

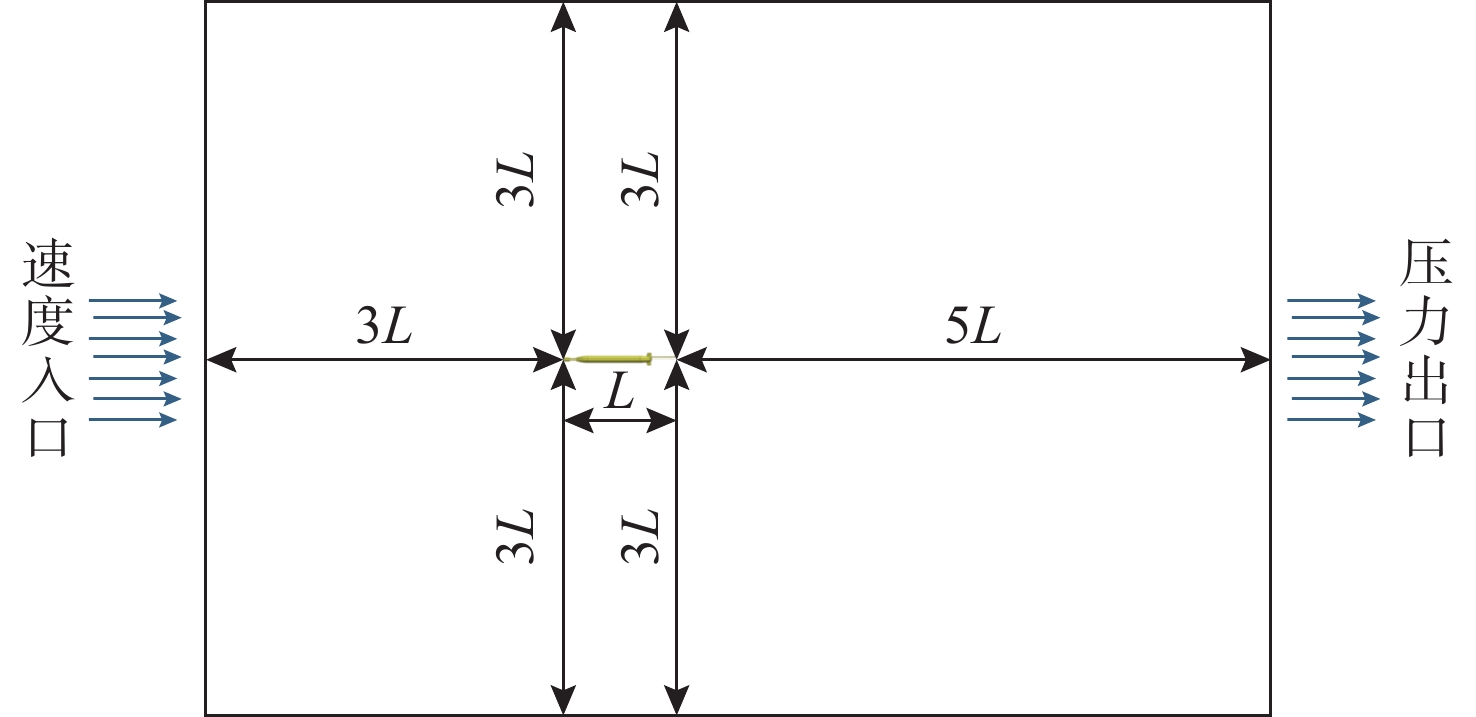
Optimization Design and Simulation of Acoustic Adaptation Structure for Underwater Gliders

1.
Qingdao Innovation and Development Base, Harbin Engineering University, Qingdao 266400, China
2.
Navy Submarine Academy, Qingdao 266194, China

摘要

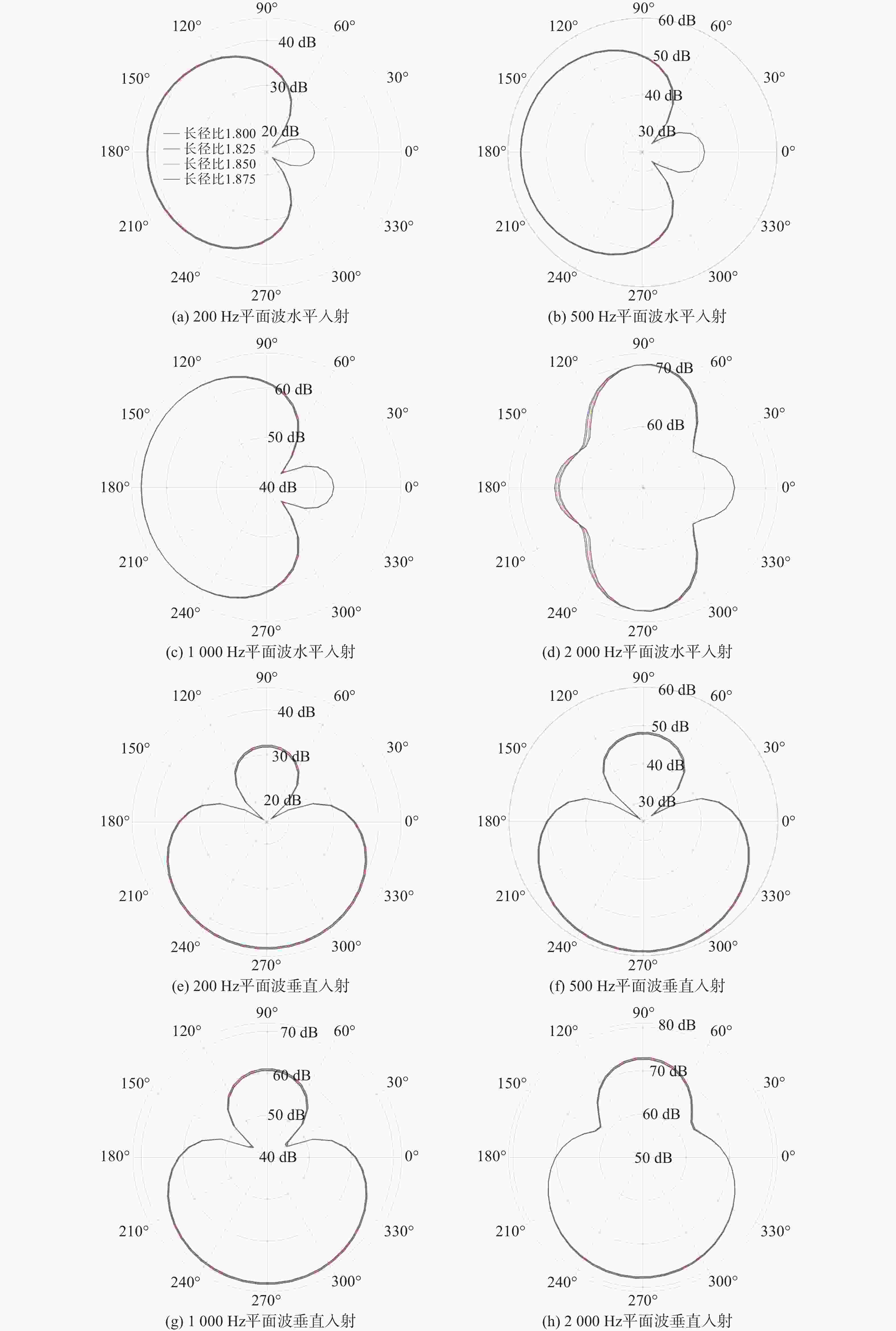
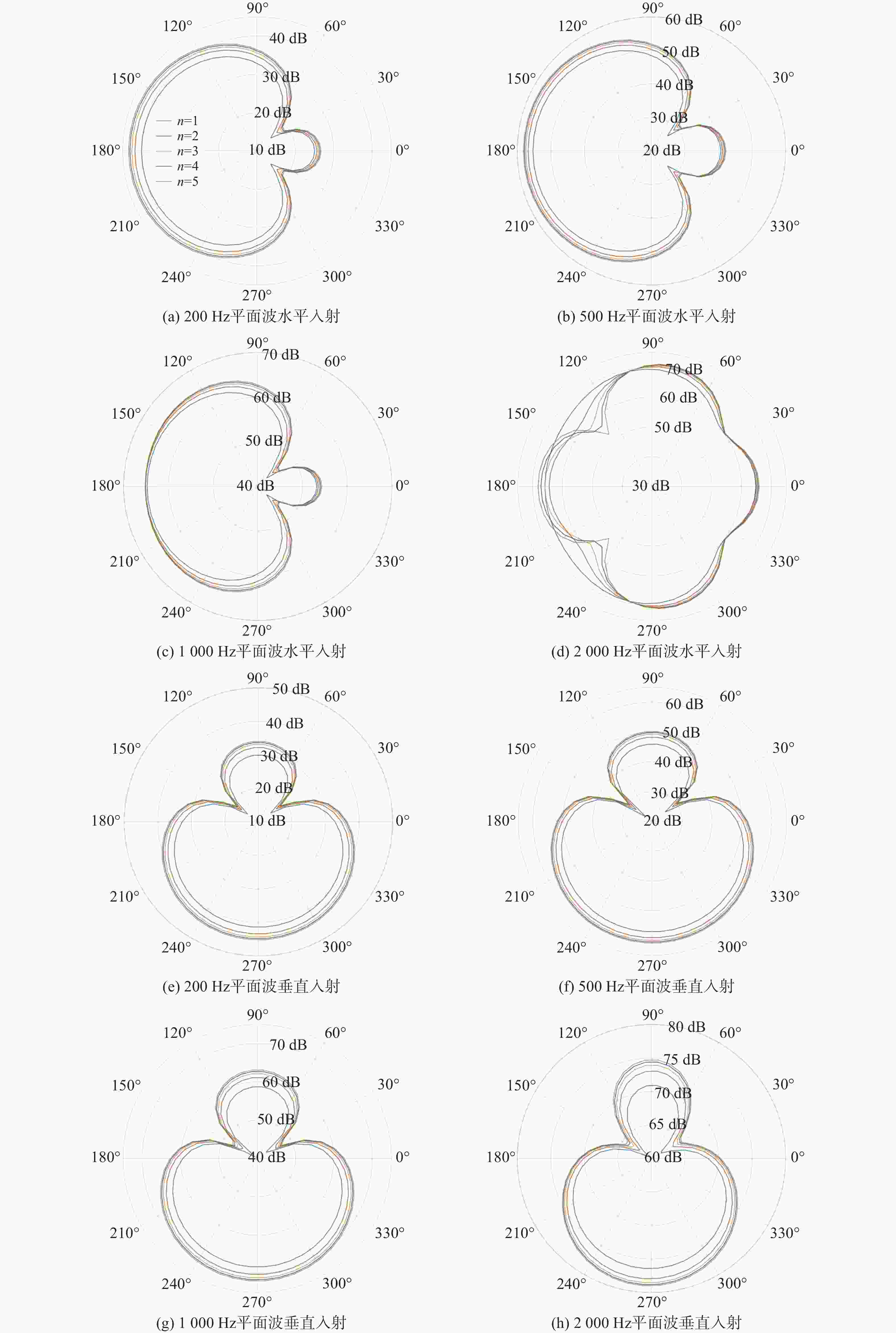
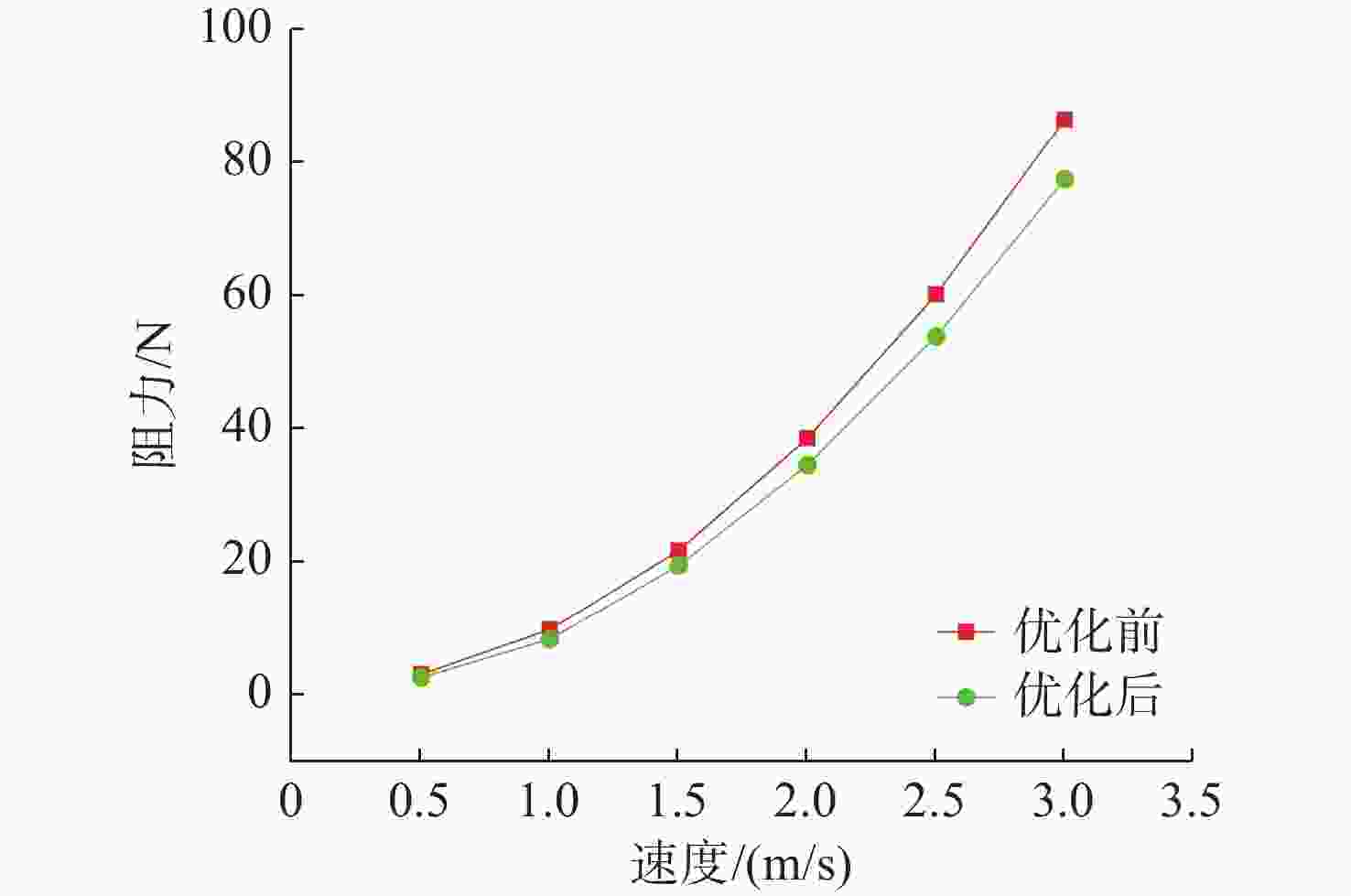
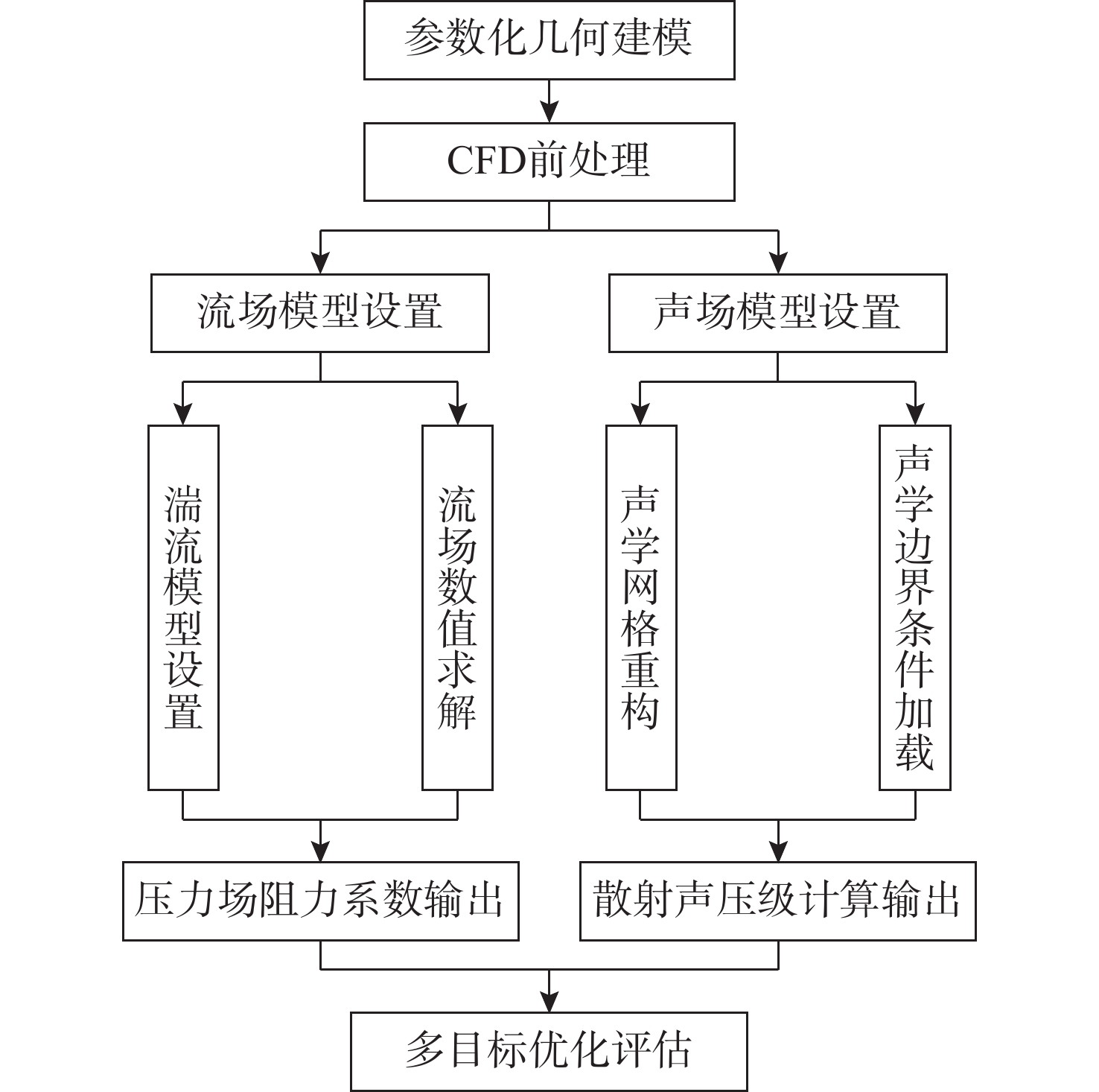
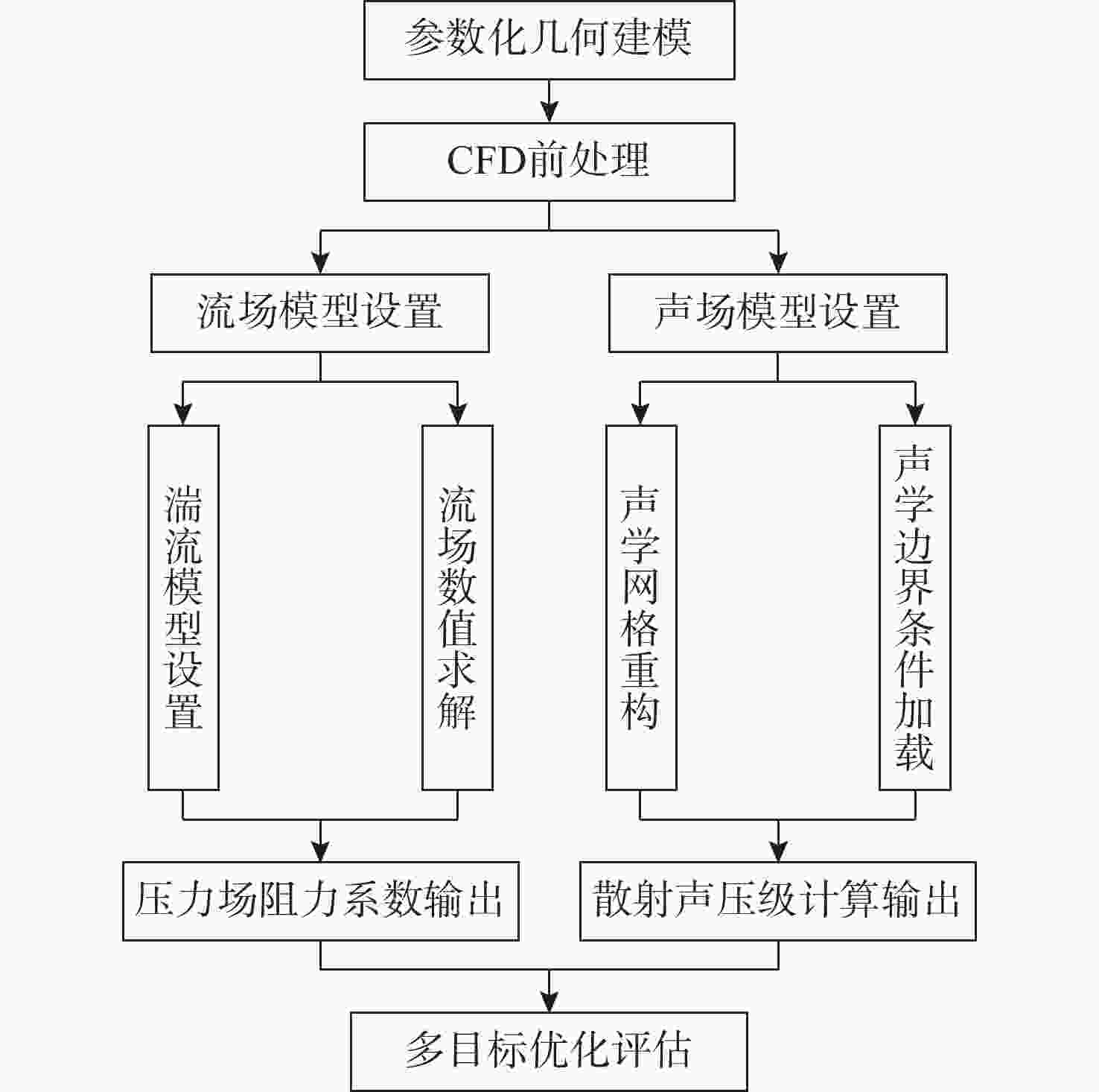
摘要: 针对长续航水下滑翔机(UG)声学适配结构设计中流体动力性能与声学探测性能难以协同优化的技术瓶颈, 提出一种融合流线型减阻与声学散射增强的双目标协同设计方法。通过构建计算流体力学-有限元法(CFD-FEM)多物理场联合仿真框架, 创新性地整合任意区域湍流流动-计算连续体力学(STAR-CCM+)粘性流体求解器与COMSOL Multiphysics声固耦合模型, 突破传统单学科优化局限, 实现流体动力特性与声场散射特征的全耦合分析。基于Myring线型方程建立参数化几何模型, 引入锐度因子和长径比作为关键设计变量, 采用智能优化算法开展多目标协同寻优。研究结果表明: 优化后的声学适配结构在0.5~3 m/s航速范围内总阻力降低10.4%~15.6%, 其中长径比为1.875、锐度因子n=2的构型在1 m/s航速下阻力降低至8.178 N; 声学性能方面, 2 000 Hz平面波入射时散射声压级提升1.5 dB, 旁瓣抑制能力增强2~3 dB, 声学接收指向性提升显著。通过攻角试验验证, 优化方案在±10°攻角范围内保持阻力降幅6%~17%, 有效解决了传统设计中流体阻力与声学性能的耦合冲突。文中研究构建的“流-固-声”多物理场协同优化范式, 为新一代长航时-强探测复合型UG的工程化设计提供了理论支撑, 拓展了UG多学科优化方法体系。
- 水下滑翔机 /
- 声学适配结构 /
- 外形优化设计 /
- 计算流体力学-有限元法联合仿真
Abstract: To address the technical bottleneck in balancing hydrodynamic efficiency and acoustic detection performance during the design of acoustic adaptation structures for long-endurance underwater gliders(UGs), this study proposed a dual-objective collaborative design method integrating computational fluid dynamics-finite element method(CFD-FEM) co-simulation. By coupling simulation of turbulent flow in arbitrary regions-computational continuum mechanics+(STAR-CCM+) for viscous flow analysis and COMSOL Multiphysics for acoustic-structure interaction, a parametric geometric model was proposed based on the Myring equation, utilizing the sharpness factor and aspect ratio as key variables. Multi-objective collaborative optimization was carried out by adopting intelligent optimization algorithms. The results indicate that the optimized acoustic adaptation structure achieves a total drag reduction of 10.4%–15.6% across a speed range of 0.5–3 m/s. Specifically, the configuration with an aspect ratio of 1.875 and a sharpness factor n = 2 exhibits a resistance reduction to 8.178 N at 1 m/s. Regarding acoustic performance, under 2 000 Hz plane wave incidence, the scattered sound pressure level increases by 1.5 dB; sidelobe suppression capability is enhanced by 2–3 dB, and acoustic reception directivity is improved significantly. Validation through angle of attack tests demonstrates that the optimized solution maintains drag reductions of 6%-17% within a ±10° angle of attack, effectively resolving the conflicting requirements between hydrodynamic resistance and acoustic performance inherent in traditional designs. The constructed “fluid-structure-acoustics” multiphysics collaborative optimization paradigm provides theoretical support for the engineering design of next-generation long-endurance, high-detection, and composite UGs and expands the UG multidisciplinary optimization methodology system.
- underwater glider /
- acoustic adaptation structure /
- shape optimization design /
- computational fluid dynamics-finite element method co-simulation

HTML全文

图 1 联合仿真技术路径图

Figure 1. Technical path diagram of joint simulation

下载: 全尺寸图片幻灯片

图 2 水下滑翔机模型

Figure 2. Model of UG

下载: 全尺寸图片幻灯片

图 3 锐度因子演变规律

Figure 3. Evolution law of sharpness factor

下载: 全尺寸图片幻灯片

图 4 计算区域二维示意图

Figure 4. 2D schematic diagram of computational region

下载: 全尺寸图片幻灯片

图 5 网格截面示意图

Figure 5. Schematic diagram of the grid cross-section

下载: 全尺寸图片幻灯片

图 6 声学适配结构阻力系数随长径比变化图

Figure 6. Variation of resistance coefficient of acoustic adaptive structure with aspect ratio

下载: 全尺寸图片幻灯片

图 7 声学适配结构阻力系数随锐度因子变化图

Figure 7. Variation of resistance coefficient of acoustic adaptive structure with sharpness factor

下载: 全尺寸图片幻灯片

图 8 声学适配结构xy平面散射声压级随长径比变化图

Figure 8. Variation of scattering sound pressure level in the xy plane of the acoustic adaptive structure with aspect ratio

下载: 全尺寸图片幻灯片

图 9 声学适配结构xy平面散射声压级随锐度因子变化图

Figure 9. Variation of sound pressure level in xy plane scattering of acoustic adaptive structure with sharpness factor

下载: 全尺寸图片幻灯片

图 10 优化后的UG三维模型

Figure 10. Optimized 3D model of UG

下载: 全尺寸图片幻灯片

图 11 速度-阻力对比曲线图

Figure 11. The comparison curves between speed and resistance

下载: 全尺寸图片幻灯片

图 12 攻角-阻力对比曲线

Figure 12. Comparison curves between attack angle and resistance

下载: 全尺寸图片幻灯片

图 13 攻角-力矩对比曲线

Figure 13. Comparison curves between angle of attack and torque

下载: 全尺寸图片幻灯片

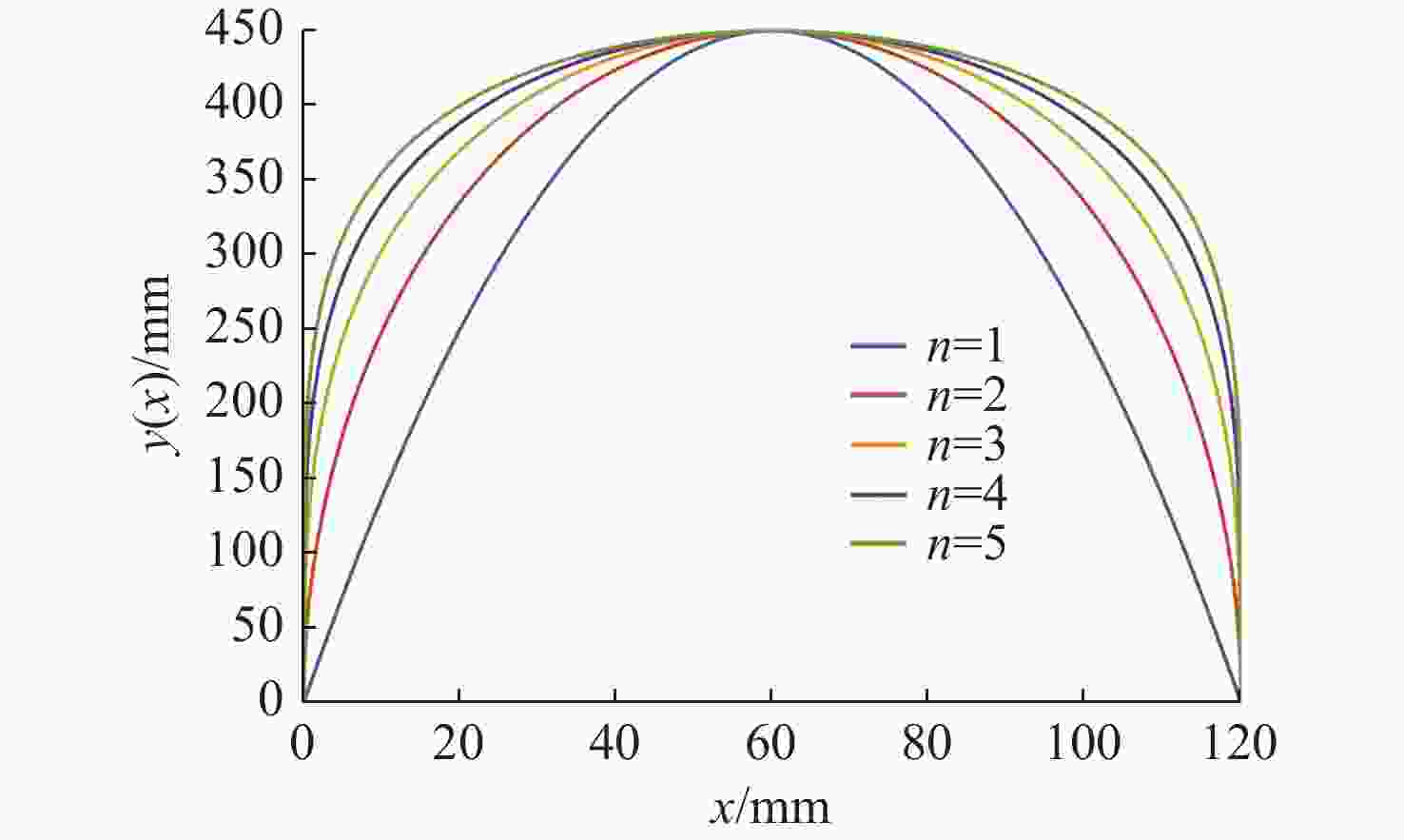
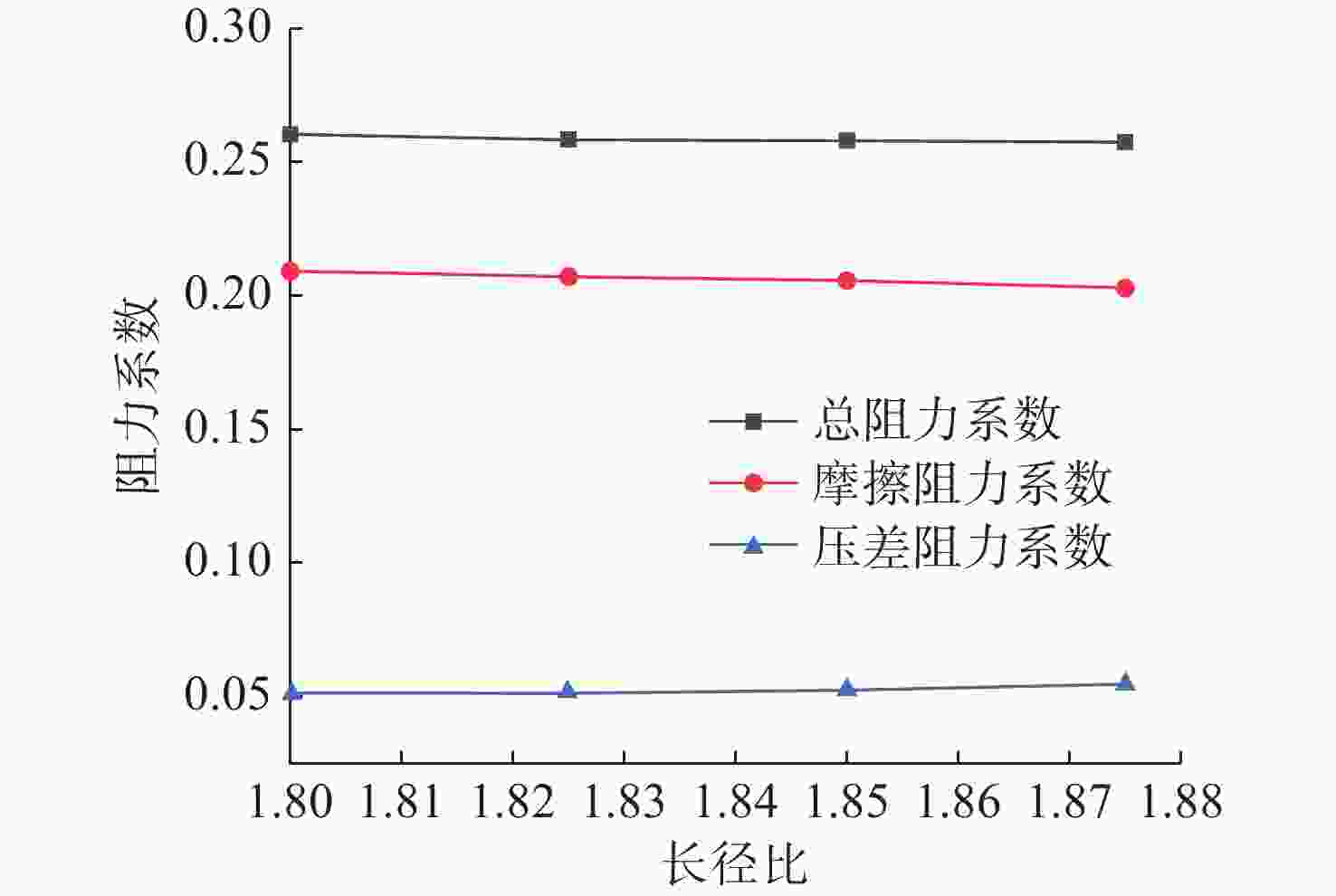
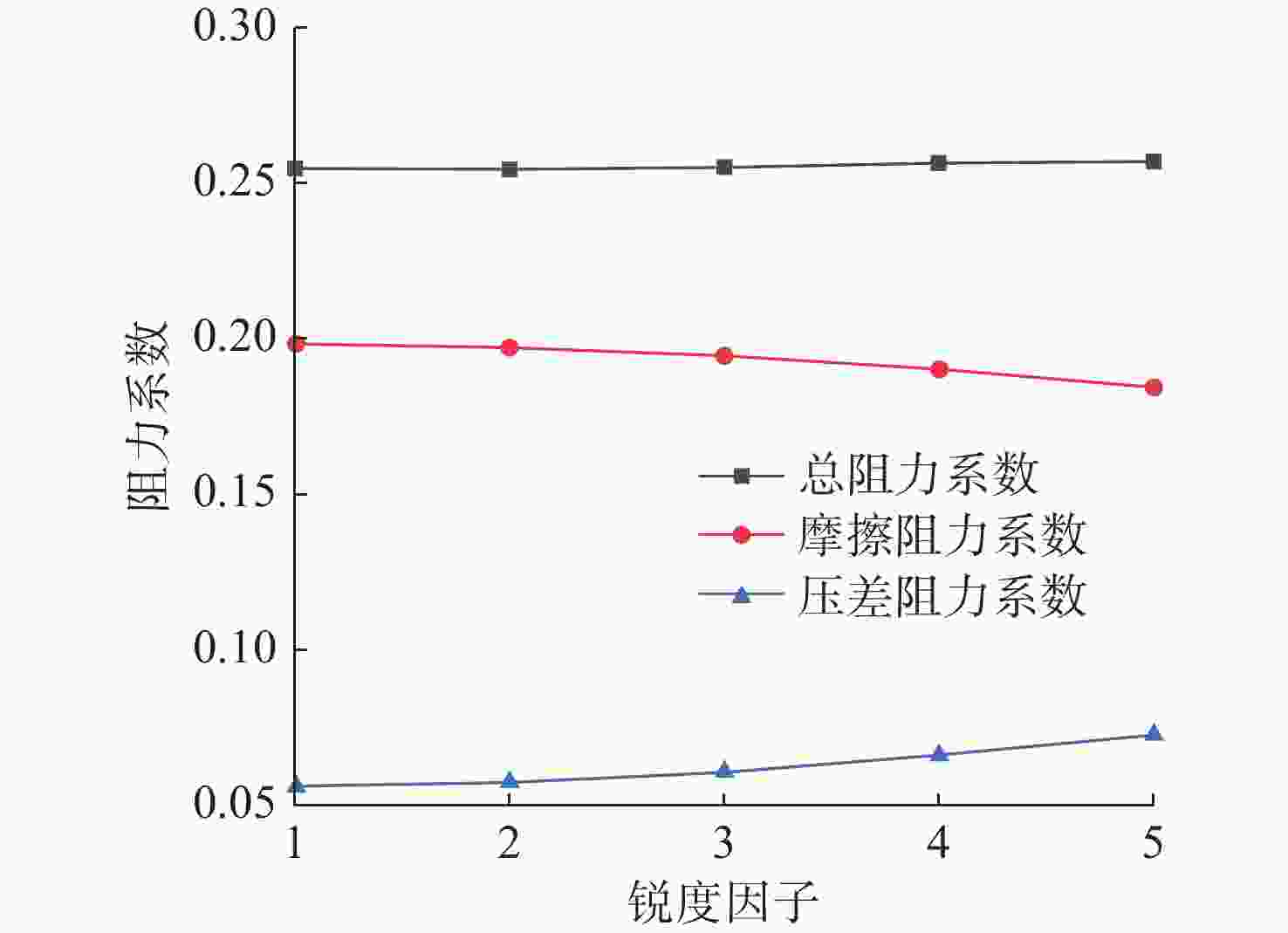
表 1 声学适配结构设计矩阵表

Table 1. Matrix of acoustic adaptive structure design

声学适配结构长径比	声学适配结构长度 /mm	整机长度 /mm	整机长径比
1.800	432	2 967	12.36
1.825	438	2 973	12.39
1.850	444	2 979	12.41
1.875	450	2 985	12.44

下载: 导出CSV

表 2 网格无关性验证

Table 2. Mesh independence verification

网格数量	总阻力/N
2.4989×10⁶	14.367
3.5334×10⁶	11.124
4.9963×10⁶	9.664
7.0648×10⁶	9.639
9.9923×10⁶	9.615

下载: 导出CSV

表 3 优化前后直航运动仿真结果对比

Table 3. Comparison of simulation results for direct flight motion before and after optimization

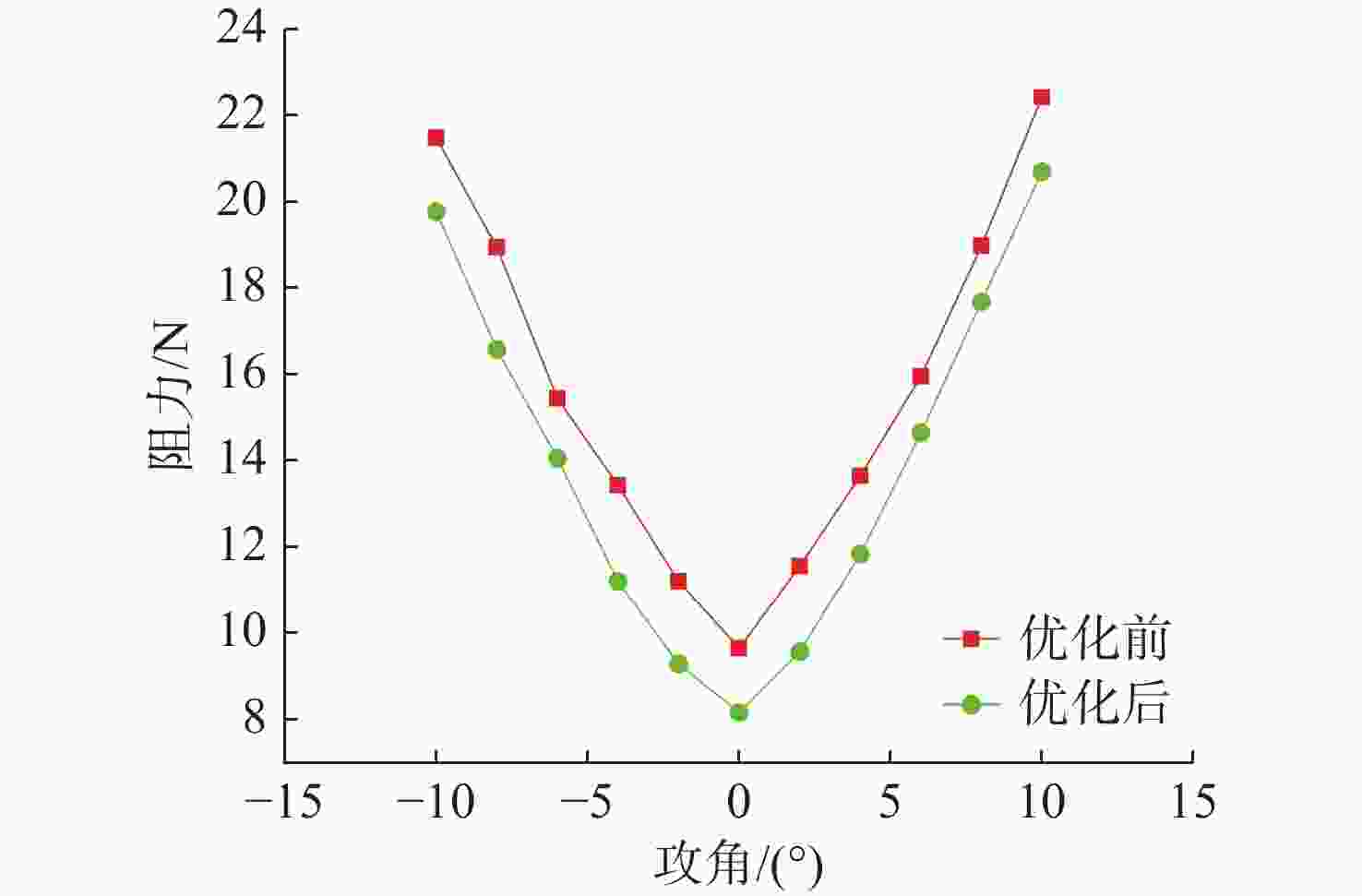
速度/(m/s)	总阻力/N
速度/(m/s)	优化前	优化后
0.5	2.887	2.436
1.0	9.664	8.178
1.5	21.593	19.344
2.0	38.451	34.436
2.5	60.003	53.748
3.0	86.364	77.341

下载: 导出CSV

表 4 优化前后斜航运动仿真结果对比

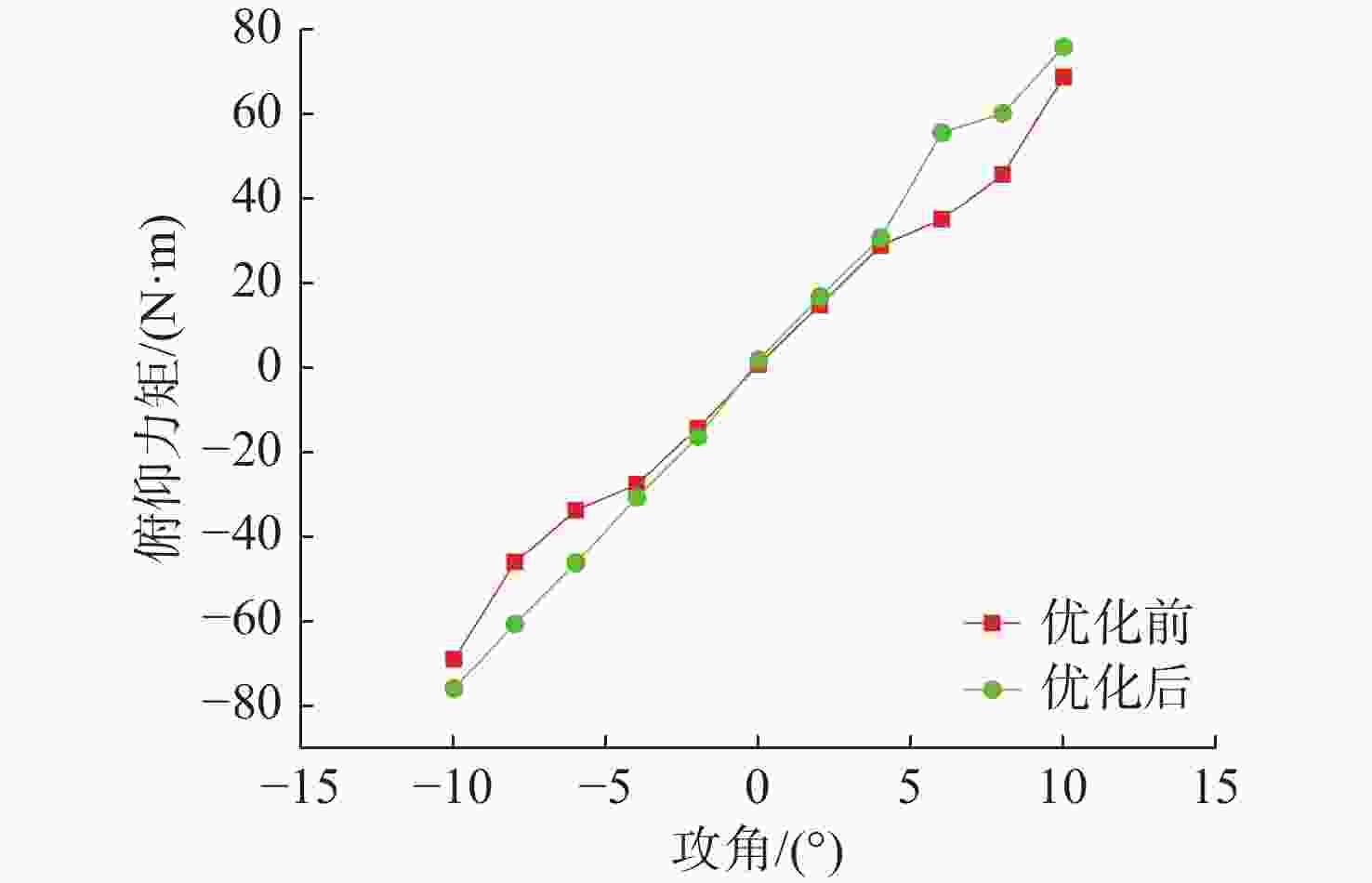
Table 4. Comparison of simulation results of oblique navigation motion before and after optimization

攻角/(°)	总阻力/N		俯仰力矩/(N·m)
攻角/(°)	优化前	优化后	优化前	优化后
10	22.459	20.726	68.785	75.912
8	19.009	17.714	45.567	60.053
6	15.981	14.673	34.867	55.504
4	13.681	11.867	28.732	30.607
2	11.583	9.586	14.737	16.685
0	9.664	8.178	0.5674	1.703
−2	11.232	9.301	−14.429	−16.609
−4	13.461	11.235	−27.862	−30.873
−6	15.471	14.089	−33.941	−46.499
−8	18.972	16.611	−46.335	−60.873
−10	21.507	19.802	−69.227	−76.225

下载: 导出CSV

参考文献(15)

[1]	MUGGLI F A, HOLBEIN P, DUPONT P. CFD calculation of a mixed flow pump characteristic from shutoff to maximum flow[J]. Journal of Fluids Engineering, 2002, 124(3): 798-802. doi: 10.1115/1.1478061
[2]	谷海涛, 林扬, 胡志强, 等. 基于代理模型的水下滑翔机机翼设计优化方法[J]. 机械工程学报, 2009, 45(12): 7-14. doi: 10.3901/JME.2009.12.007 GU H T, LIN Y, HU Z Q, et al. Design optimization method for underwater glider wings based on surrogate model[J]. Journal of Mechanical Engineering, 2009, 45(12): 7-14. doi: 10.3901/JME.2009.12.007
[3]	张博, 张宇文, 李文哲, 等. 超空泡航行体前部线型对空泡生成速度影响实验研究[J]. 西北工业大学学报, 2008(5): 540-544. doi: 10.3969/j.issn.1000-2758.2008.05.003 ZHANG B, ZHANG Y W, LI W Z, et al. Experimental study on the influence of forebody profile of supercavitating vehicle on cavitation generation speed[J]. Journal of Northwestern Polytechnical University, 2008(5): 540-544. doi: 10.3969/j.issn.1000-2758.2008.05.003
[4]	张博, 张宇文, 孙致月, 等. 超空化航行体前部外径对空泡影响的研究[J]. 西北工业大学学报, 2010, 28(6): 834-839. doi: 10.3969/j.issn.1000-2758.2010.06.006 ZHANG B, ZHANG Y W, SUN Z Y, et al. Study on the influence of forebody diameter of supercavitating vehicle on cavitation characteristics[J]. Journal of Northwestern Polytechnical University, 2010, 28(6): 834-839. doi: 10.3969/j.issn.1000-2758.2010.06.006
[5]	郑帮涛. 航行体头型对气泡附着影响的数值研究[J]. 船舶力学, 2015, 19(7): 757-764. doi: 10.3969/j.issn.1007-7294.2015.07.001 ZHENG B T. Numerical study on the influence of vehicle nose shape on bubble attachment[J]. Journal of Ship Mechanics, 2015, 19(7): 757-764. doi: 10.3969/j.issn.1007-7294.2015.07.001
[6]	SUN C, SONG B, WANG P. Parametric geometric model and shape optimization of an underwater glider with blended-wing-body[J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7(6): 995-1006. doi: 10.1515/ijnaoe-2015-0069
[7]	侯东伯, 王聪, 夏维学, 等. 弹性尾缘对超空泡航行体空泡形态与压力脉动特性影响的水洞试验研究[J]. 兵工学报, 2020, 41(3): 534-541. doi: 10.3969/j.issn.1000-1093.2020.03.014
[8]	MUHAMMAD Y J, MARK O, et al. Effect of wing form on the hudrodynamic characteristics and dynamic stability of an underwater glider[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9: 382-389. doi: 10.1016/j.ijnaoe.2016.09.010
[9]	戴鹏. 基于参数化的三体组合式自主水下航行器多目标优化设计研究[D]. 广州: 华南理工大学, 2020.
[10]	赵远辉, 李宝仁, 高磊. 水下滑翔机水动力外形优化配置[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(3): 505-508, 513.
[11]	ZHENG G C, YANG X L. Studies of the resistance optimization of underwater vehicle based on multiple-speed approximate model[J]. MATEC Web of Conferences, 2019, 272(1): 10-29.
[12]	姜宜辰, 赵月, 熊济时, 等. 水下航行器艇体形状对阻力及流噪声综合影响[J]. 哈尔滨工程大学学报, 2022, 43(1): 76-82, 138. doi: 10.11990/jheu.202008038
[13]	张帅. 长航程水下滑翔机的减阻技术研究[D]. 天津: 天津大学, 2017.
[14]	李鹏, 国瑀, 秦洪德, 等. 海底对无人水下航行器水动力性能的影响[J]. 船舶工程, 2022, 44(4): 146-153.
[15]	邹磊, 田威, 林源, 等. 基于不同湍流模型的螺旋桨水动力特性研究[J]. 船舶工程, 2023, 45(12): 94-100, 114.