Research on the Influence of JWL EOS Parameters of Explosives on Numerical Simulation of Underwater Explosion
-
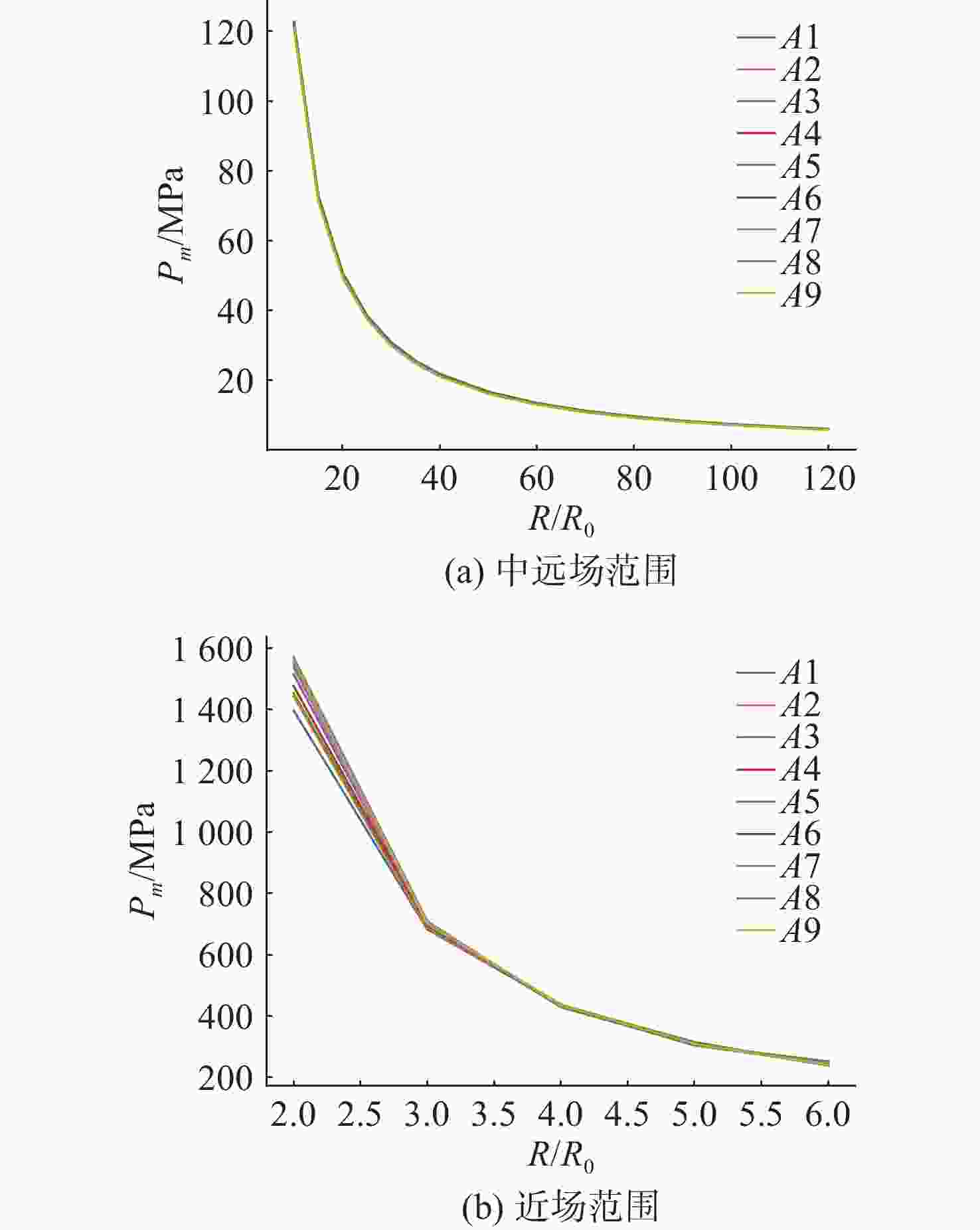
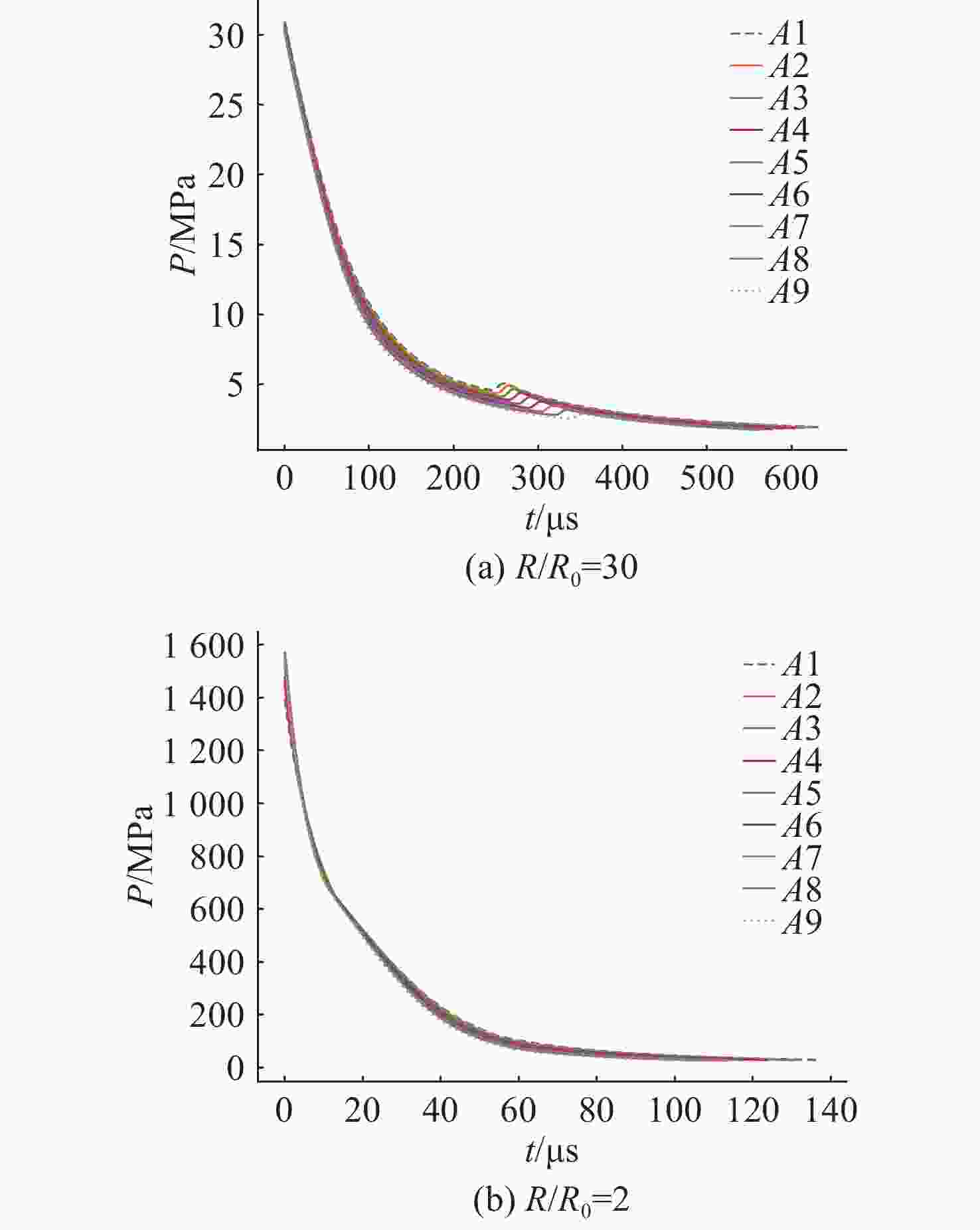
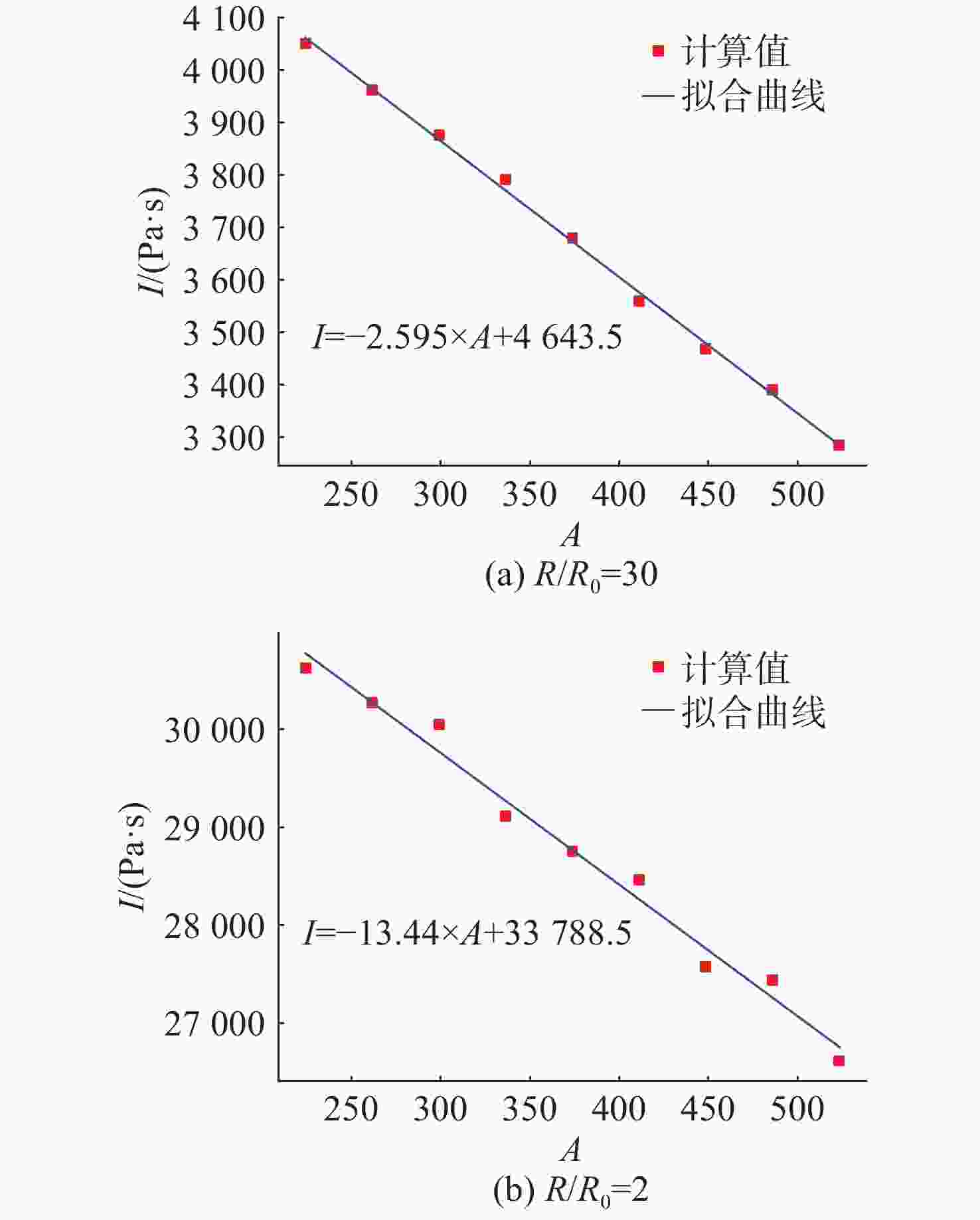
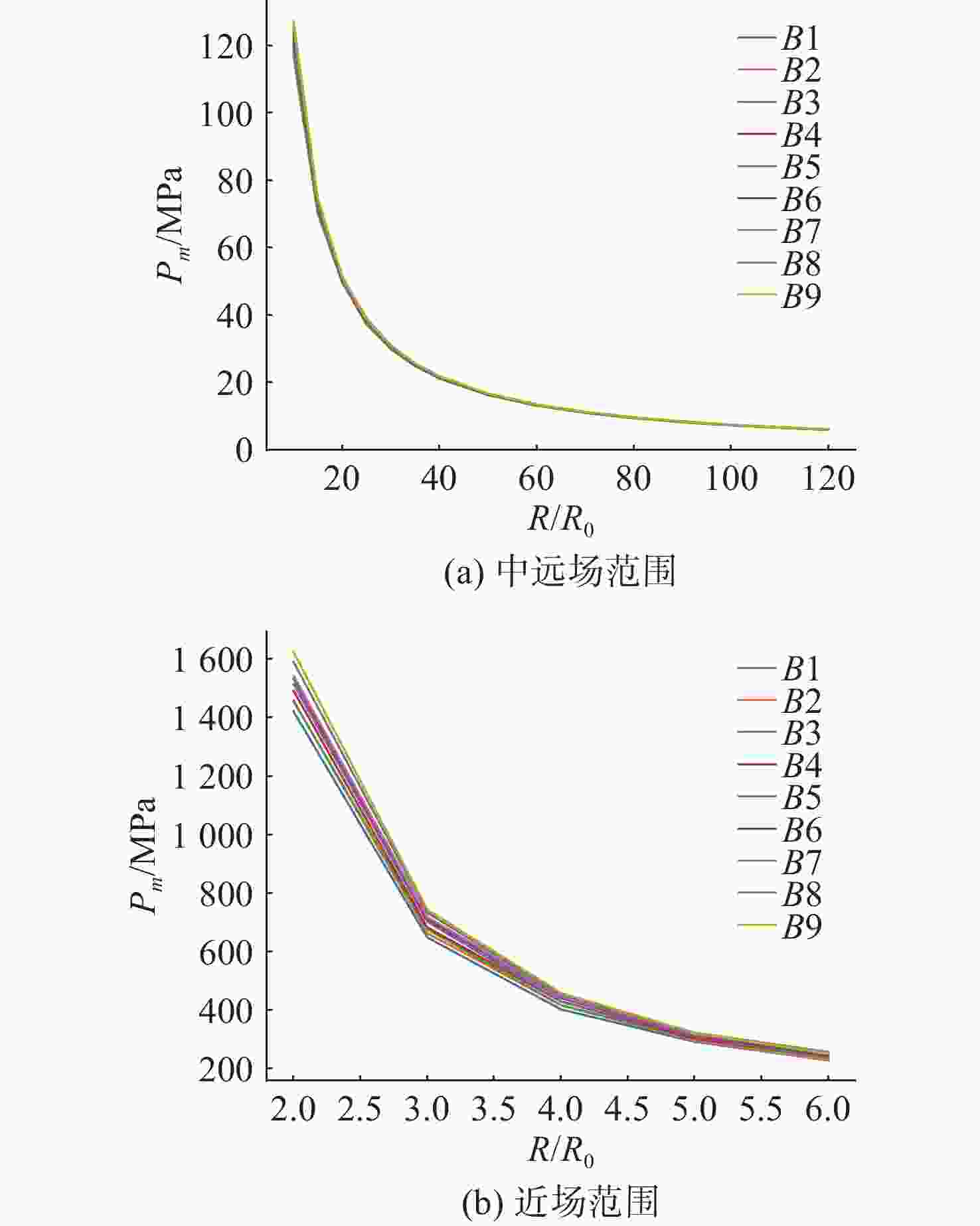
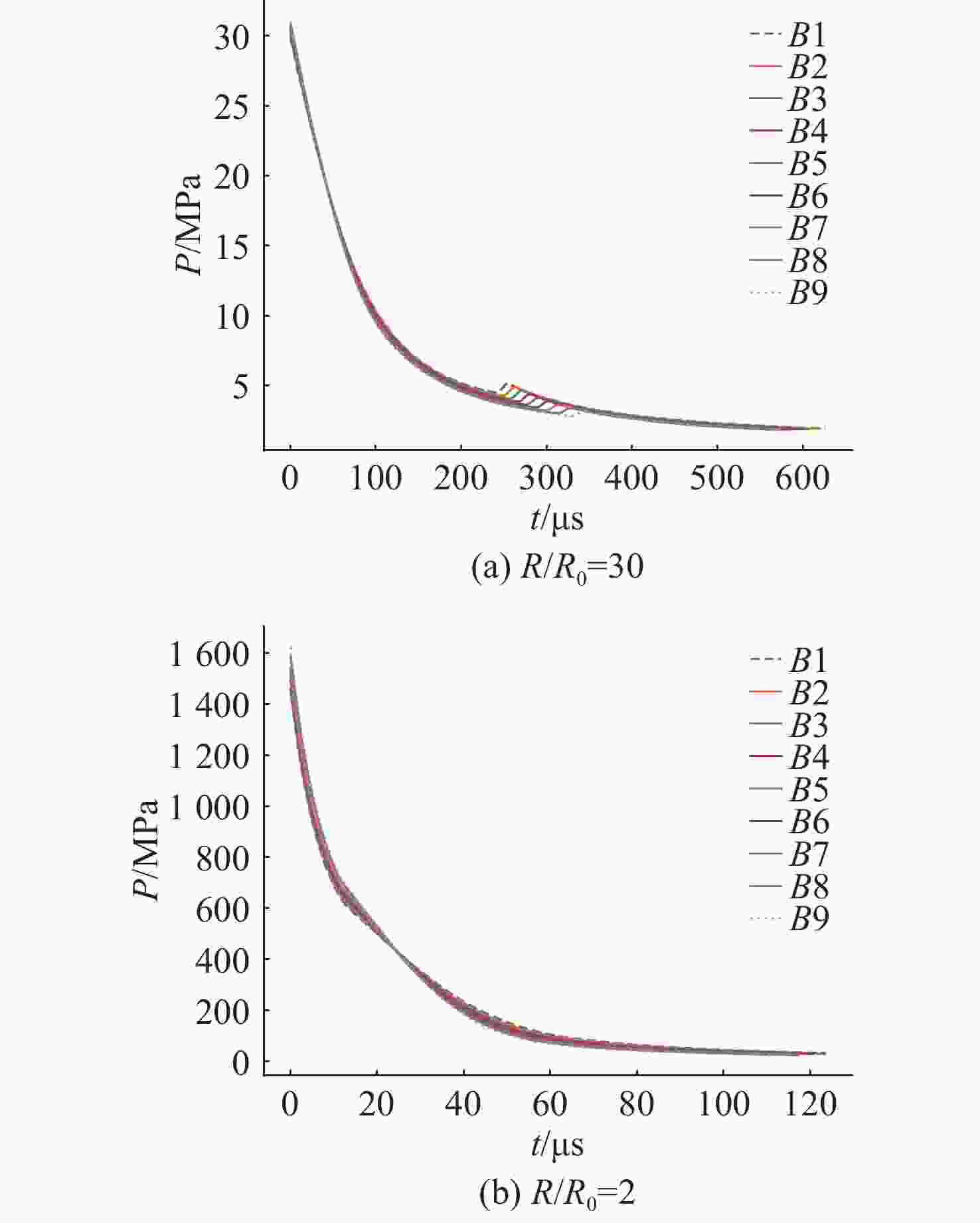
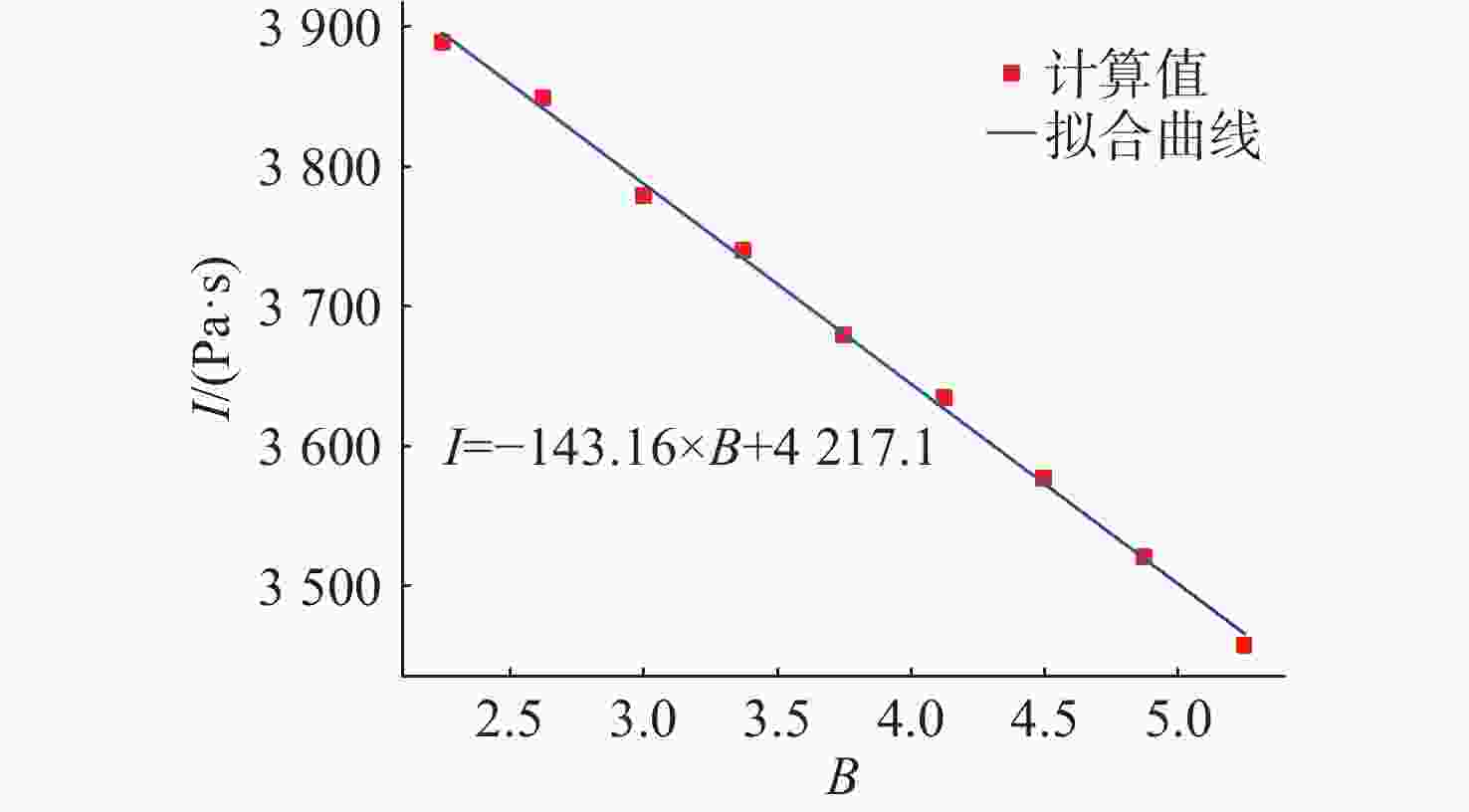
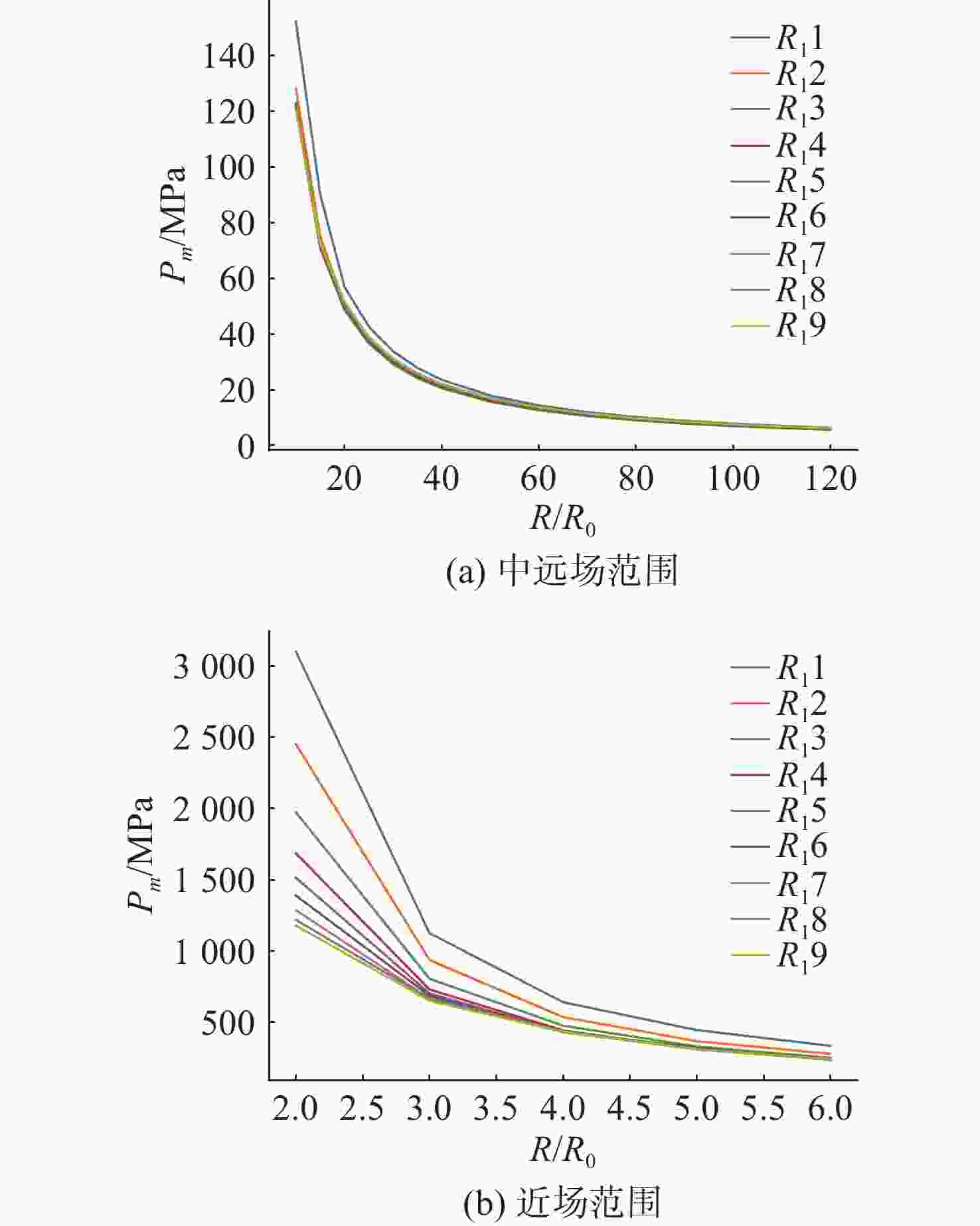
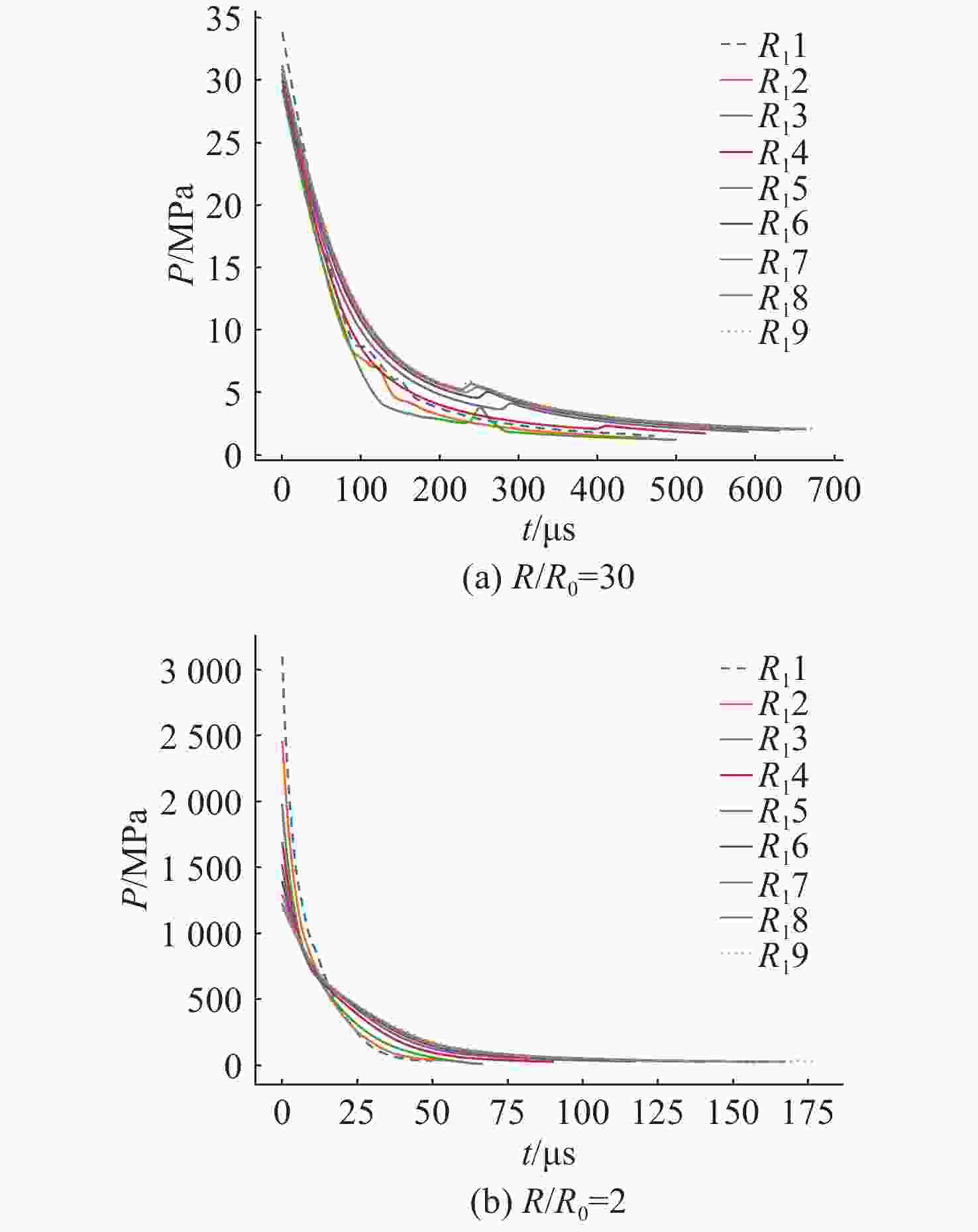
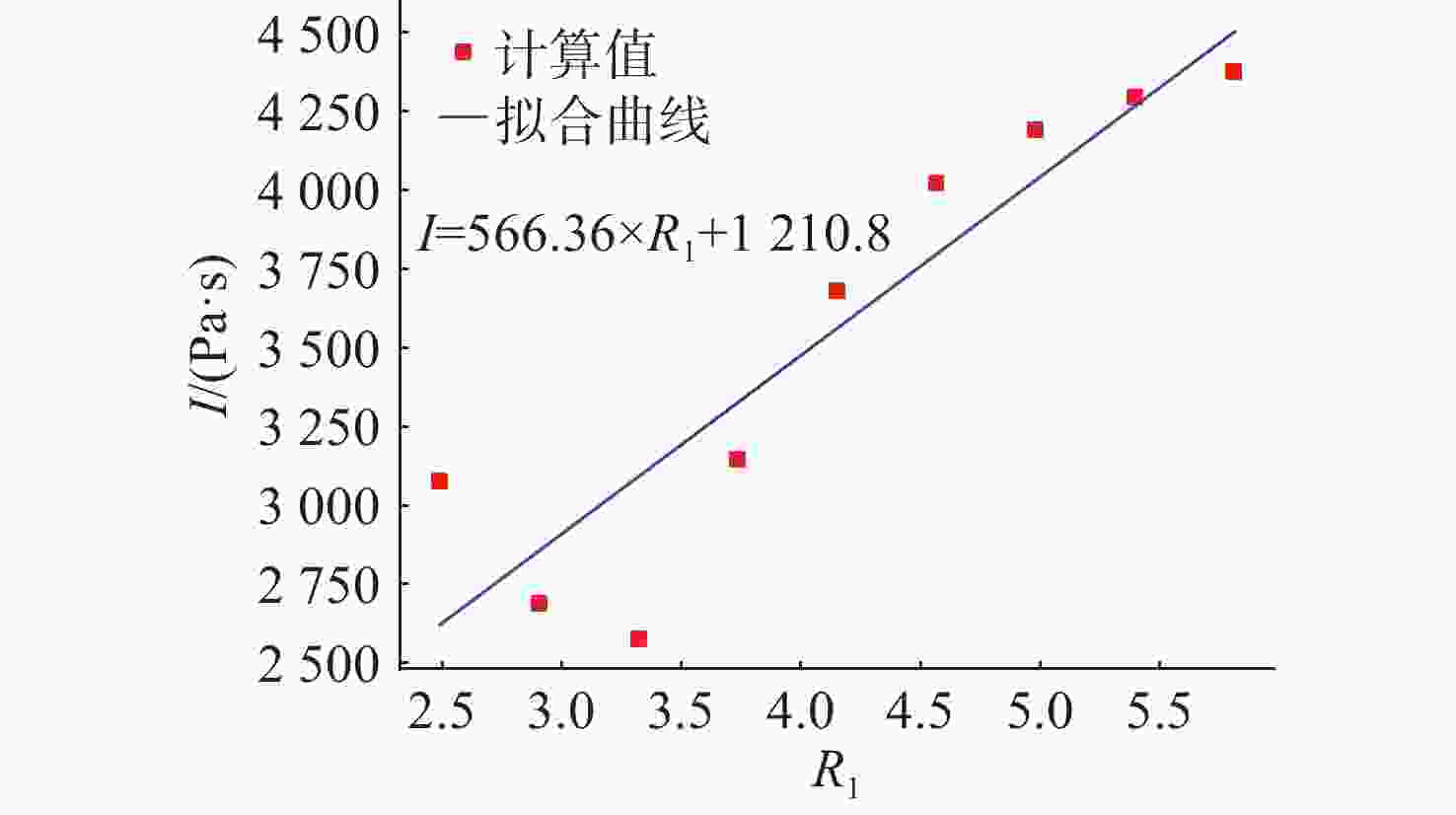
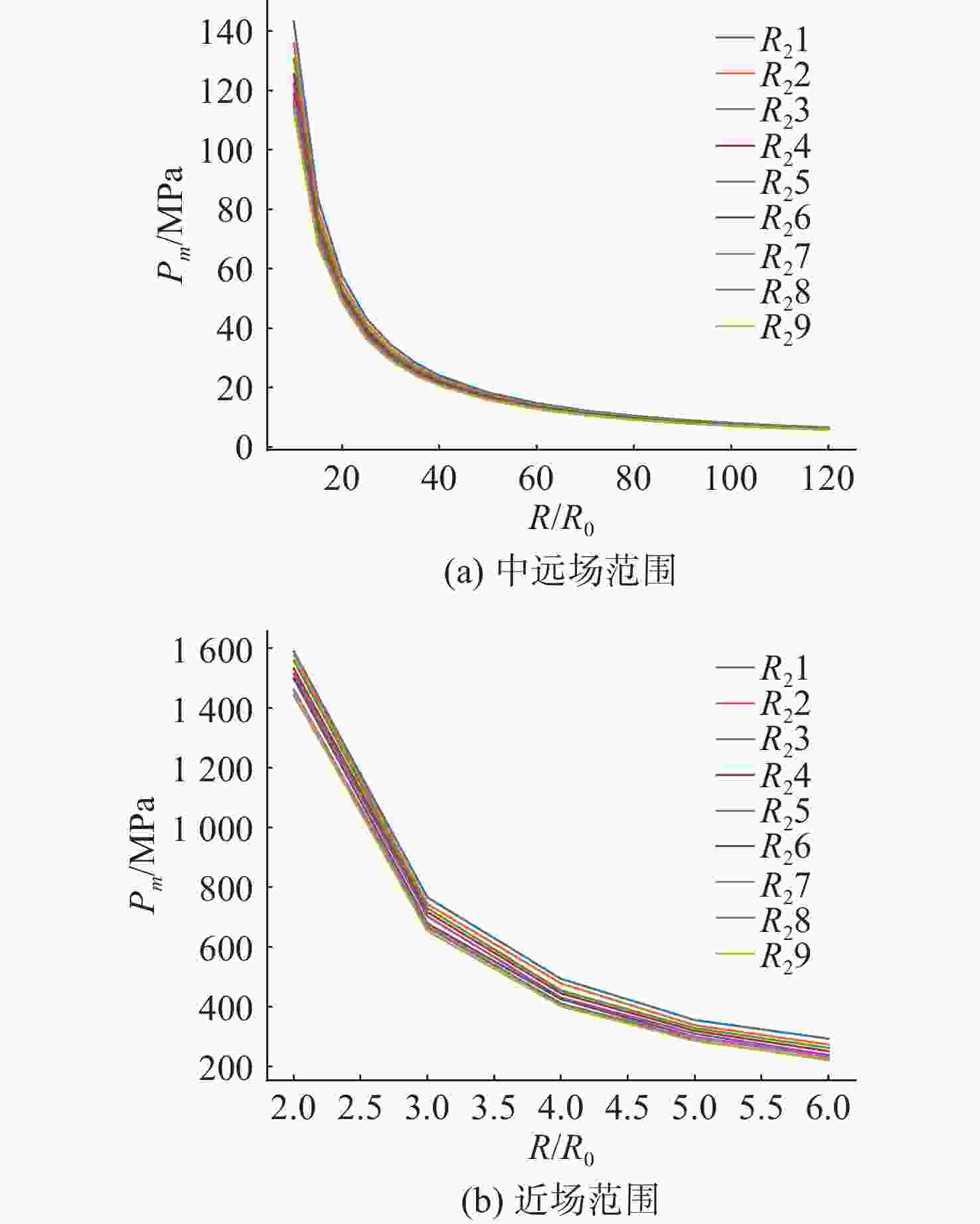
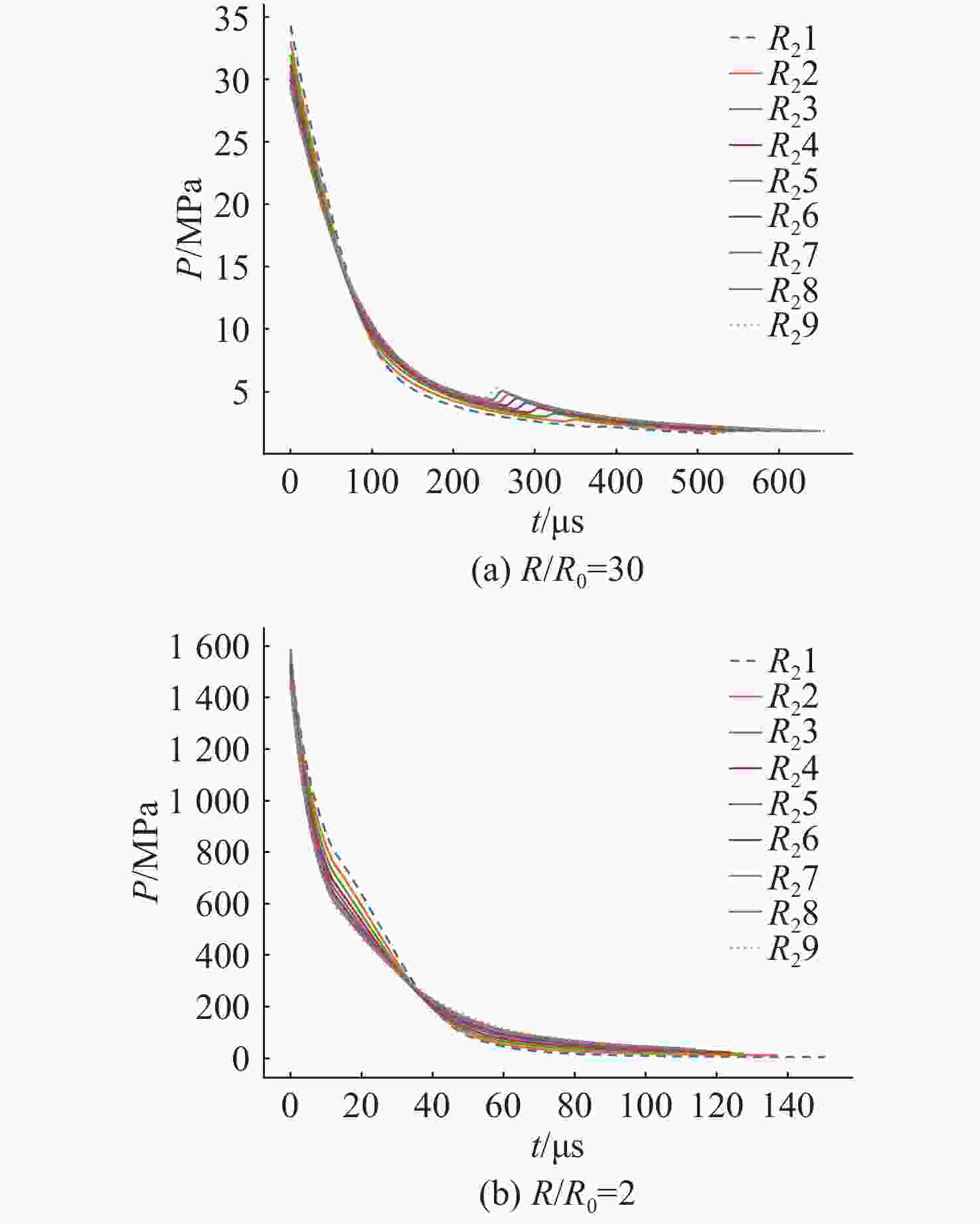
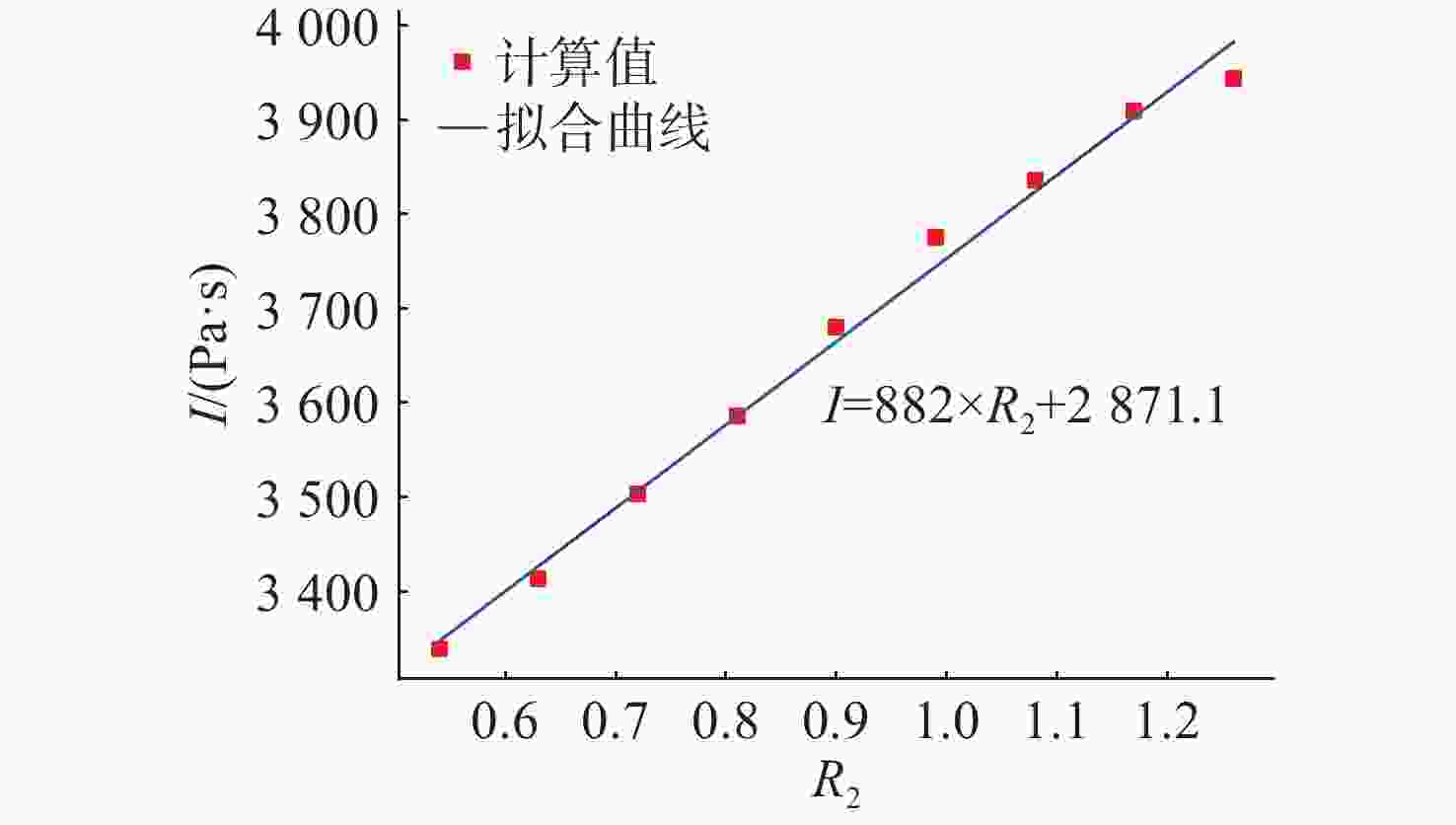
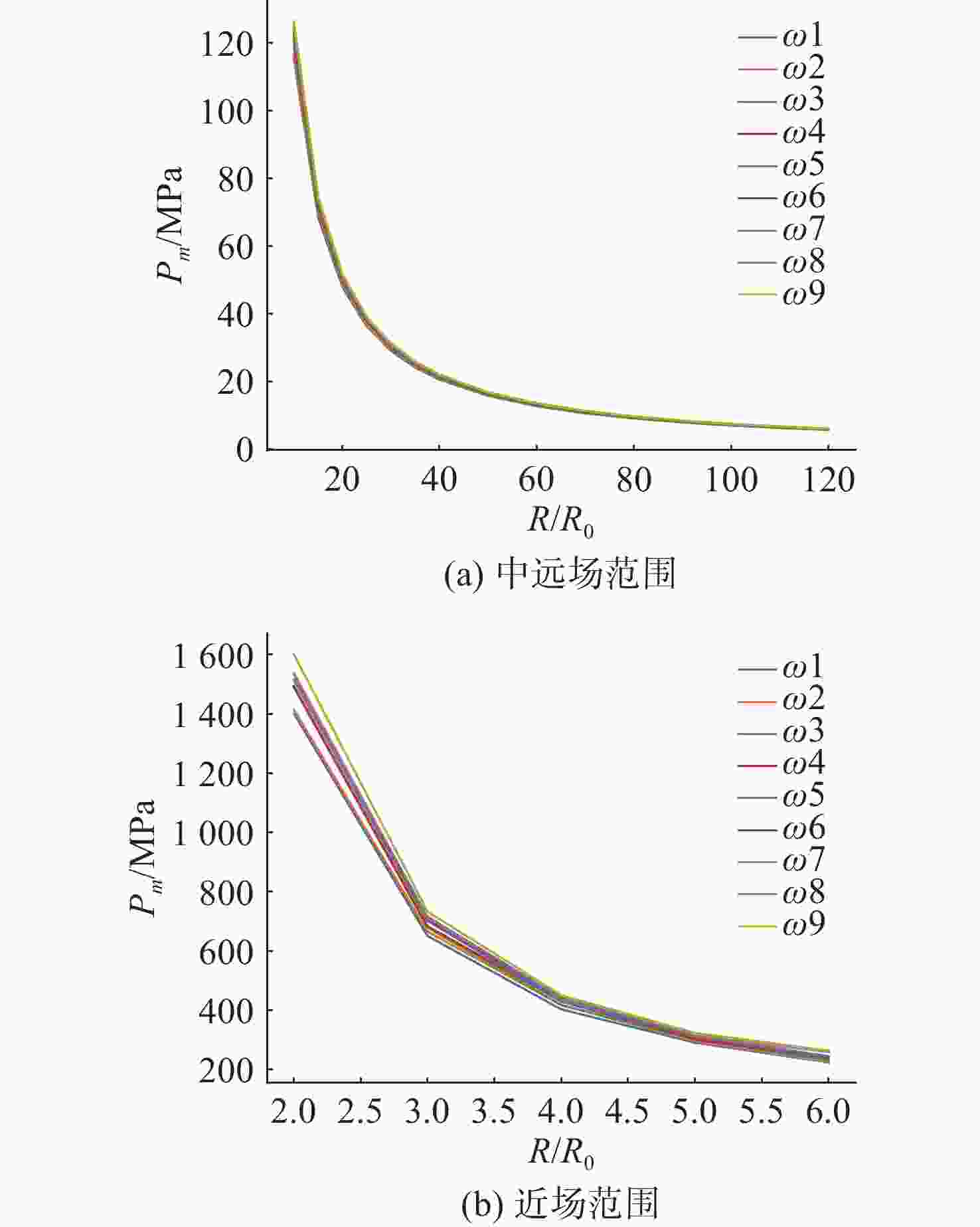
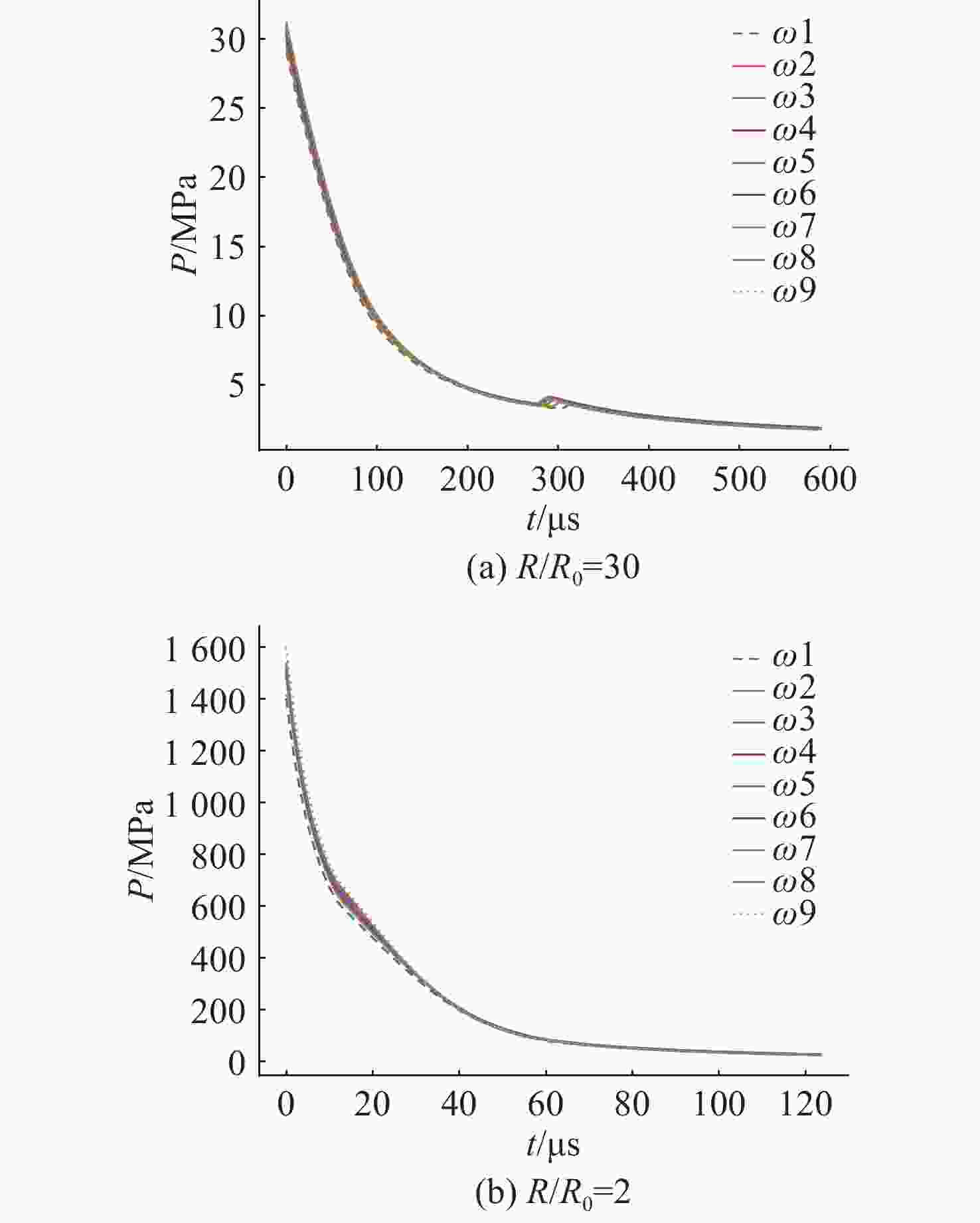
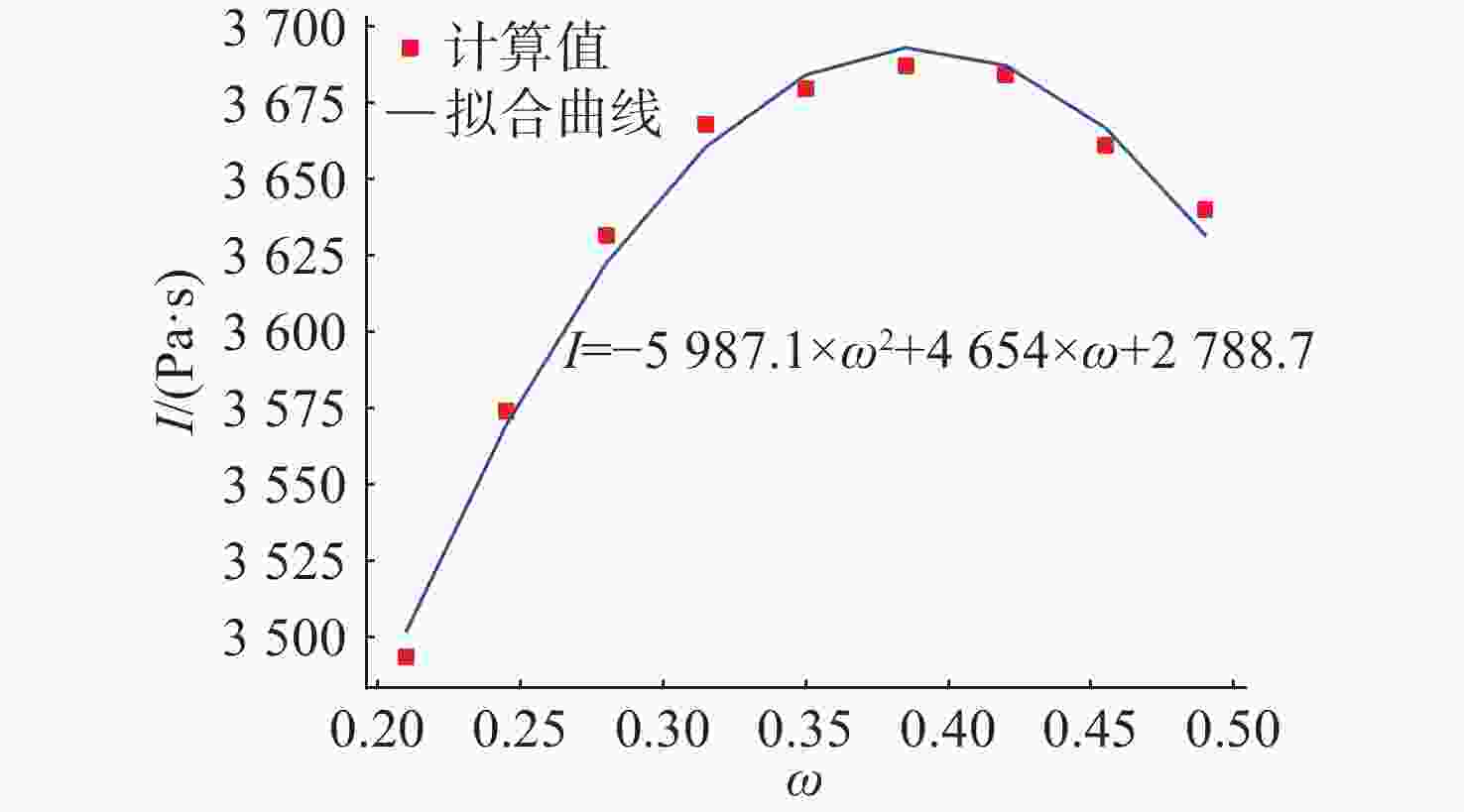
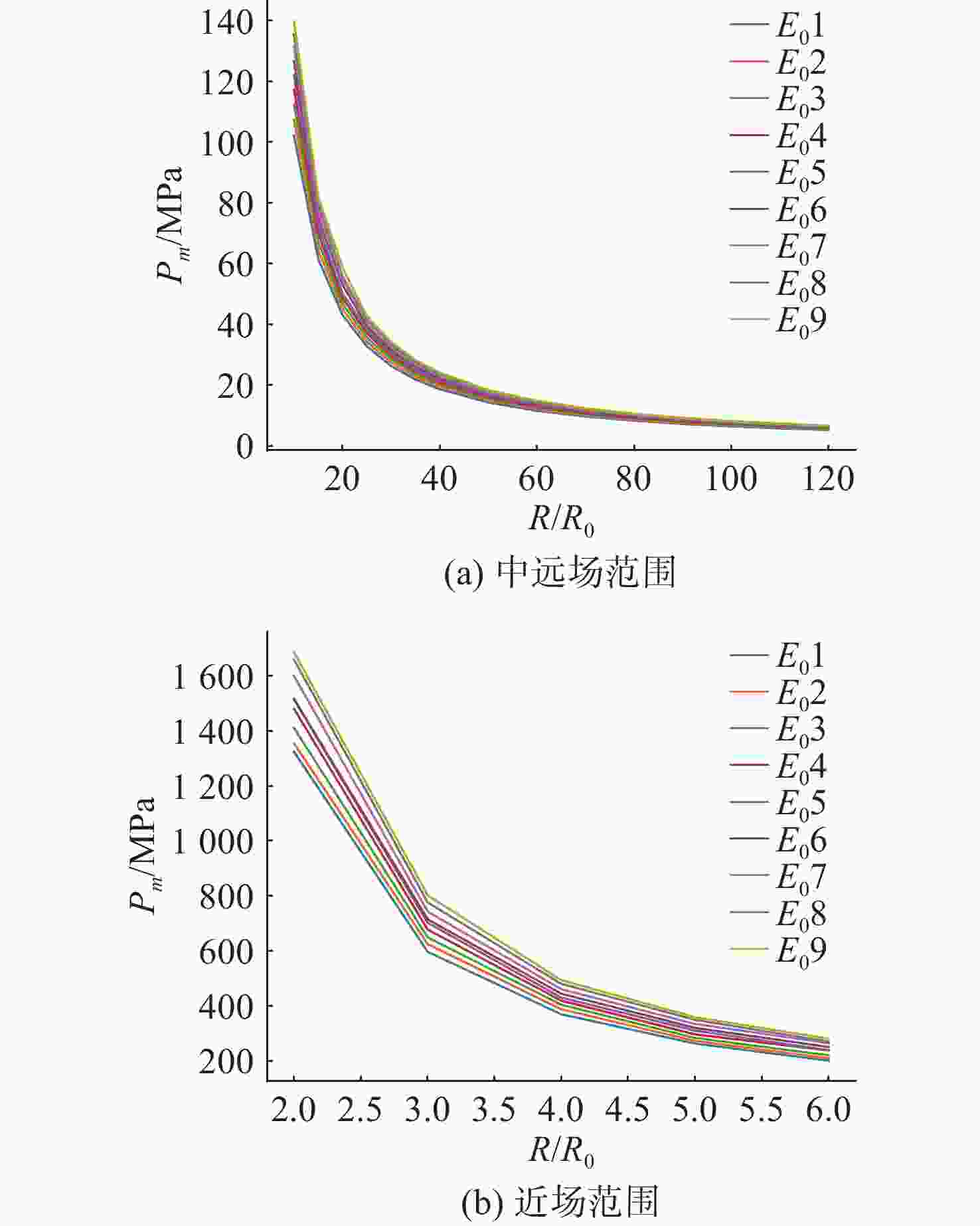
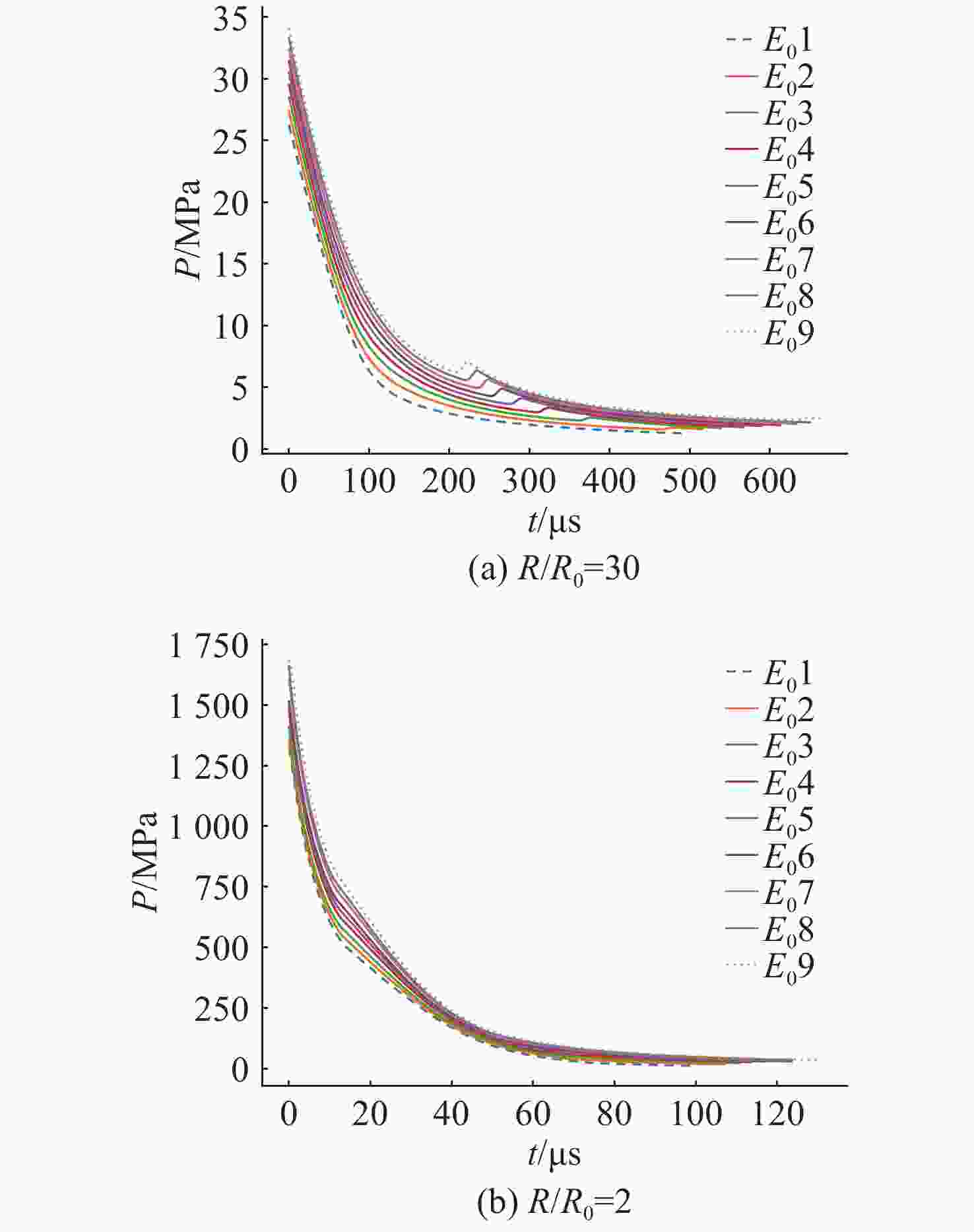
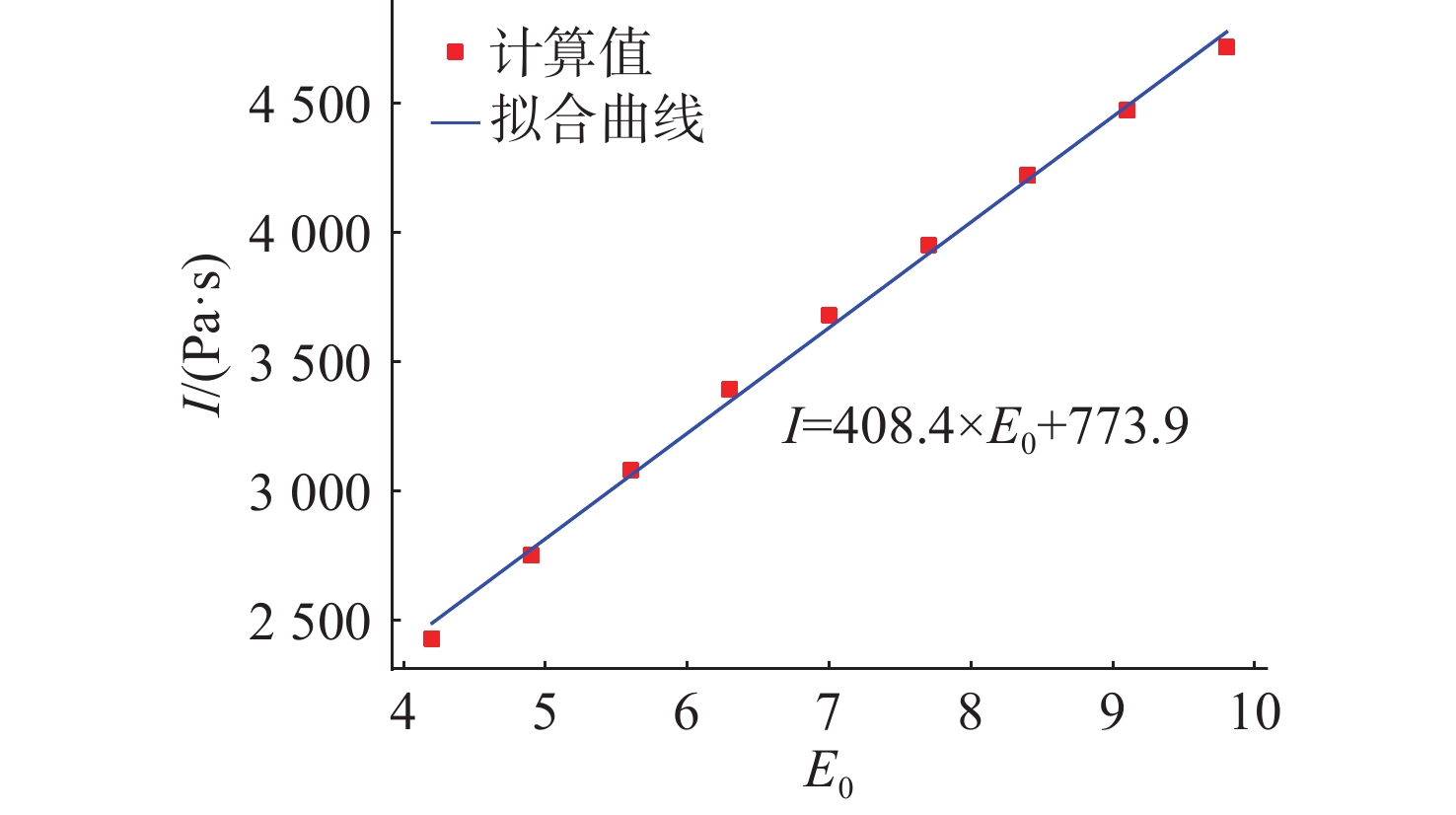
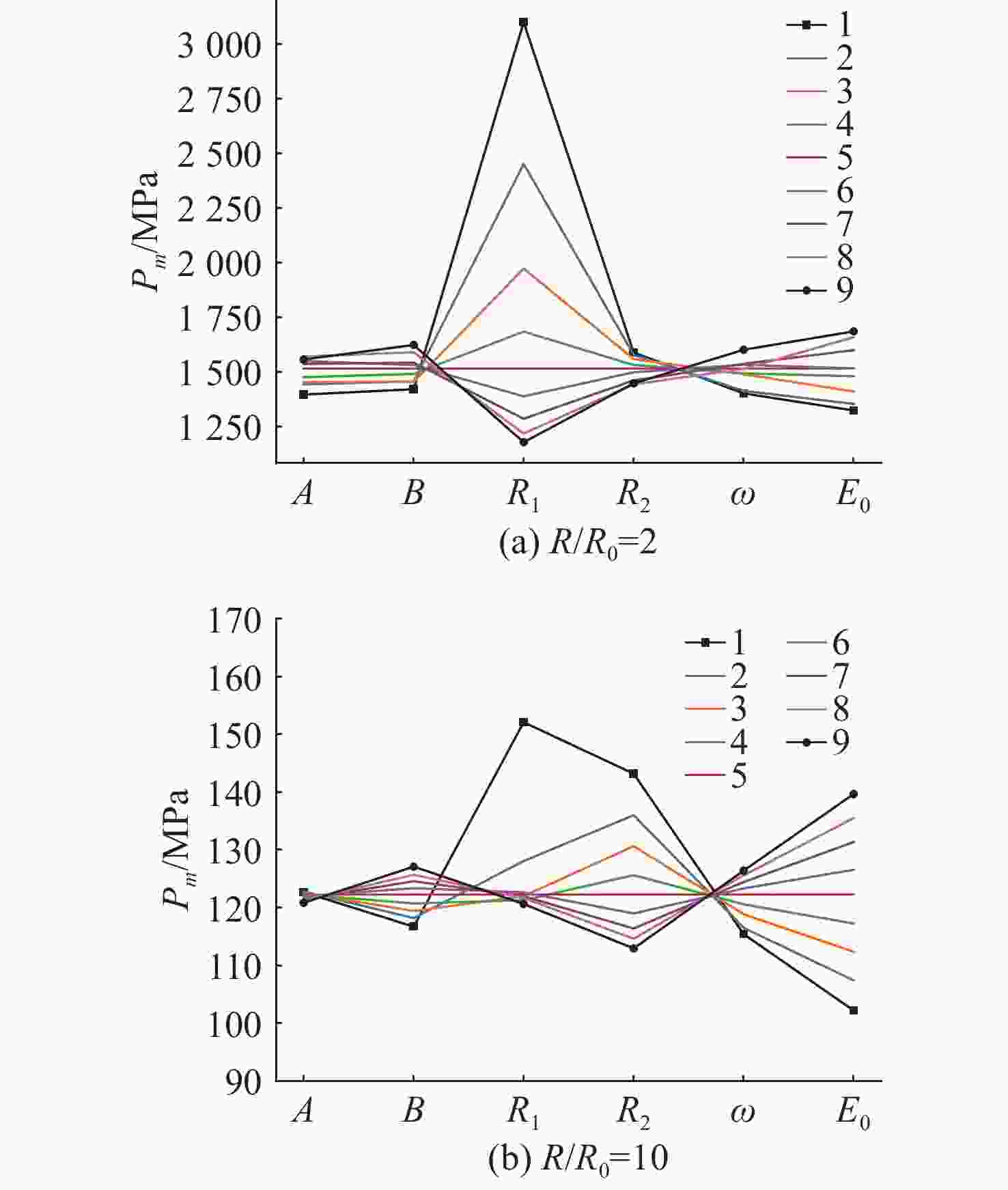
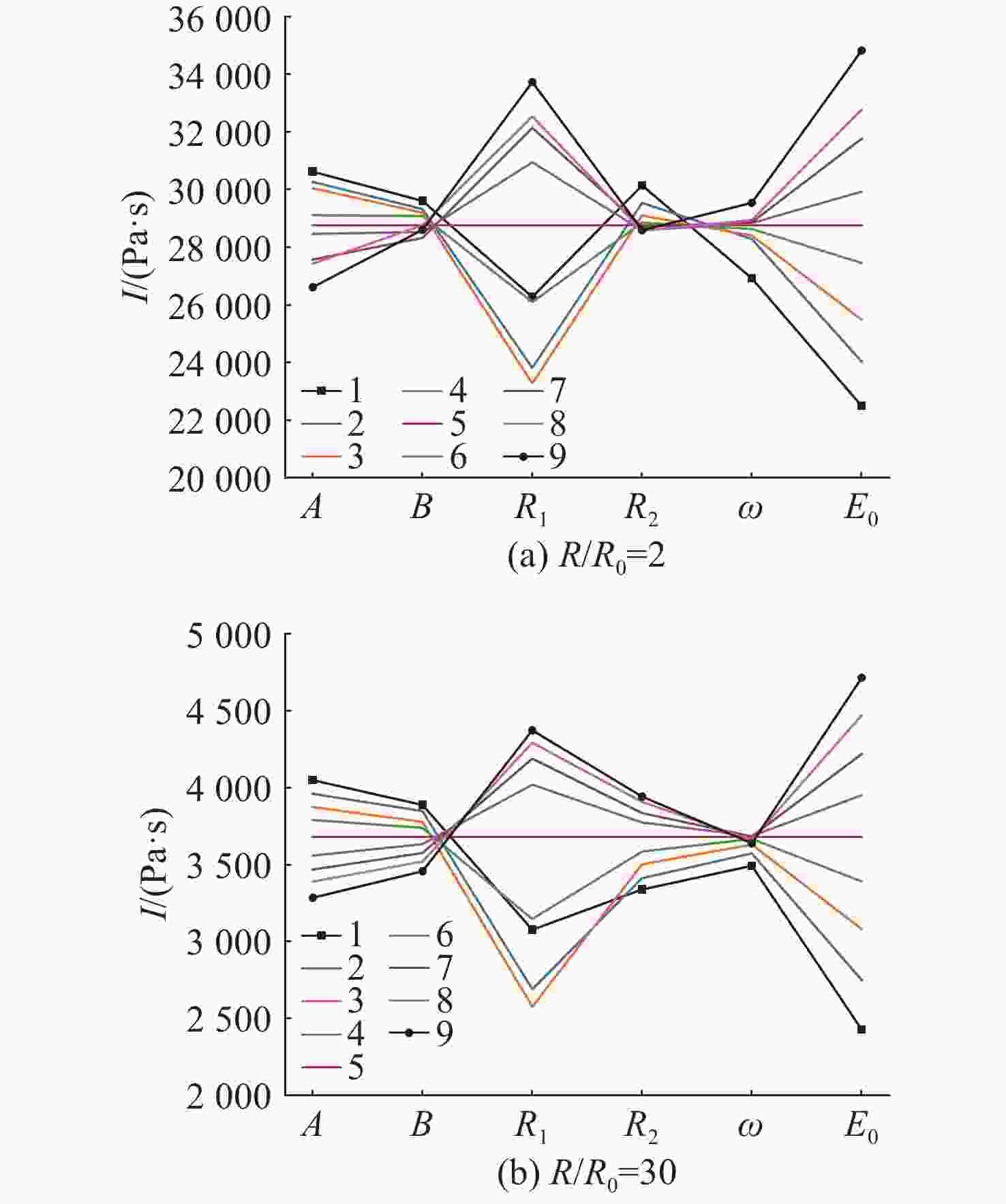
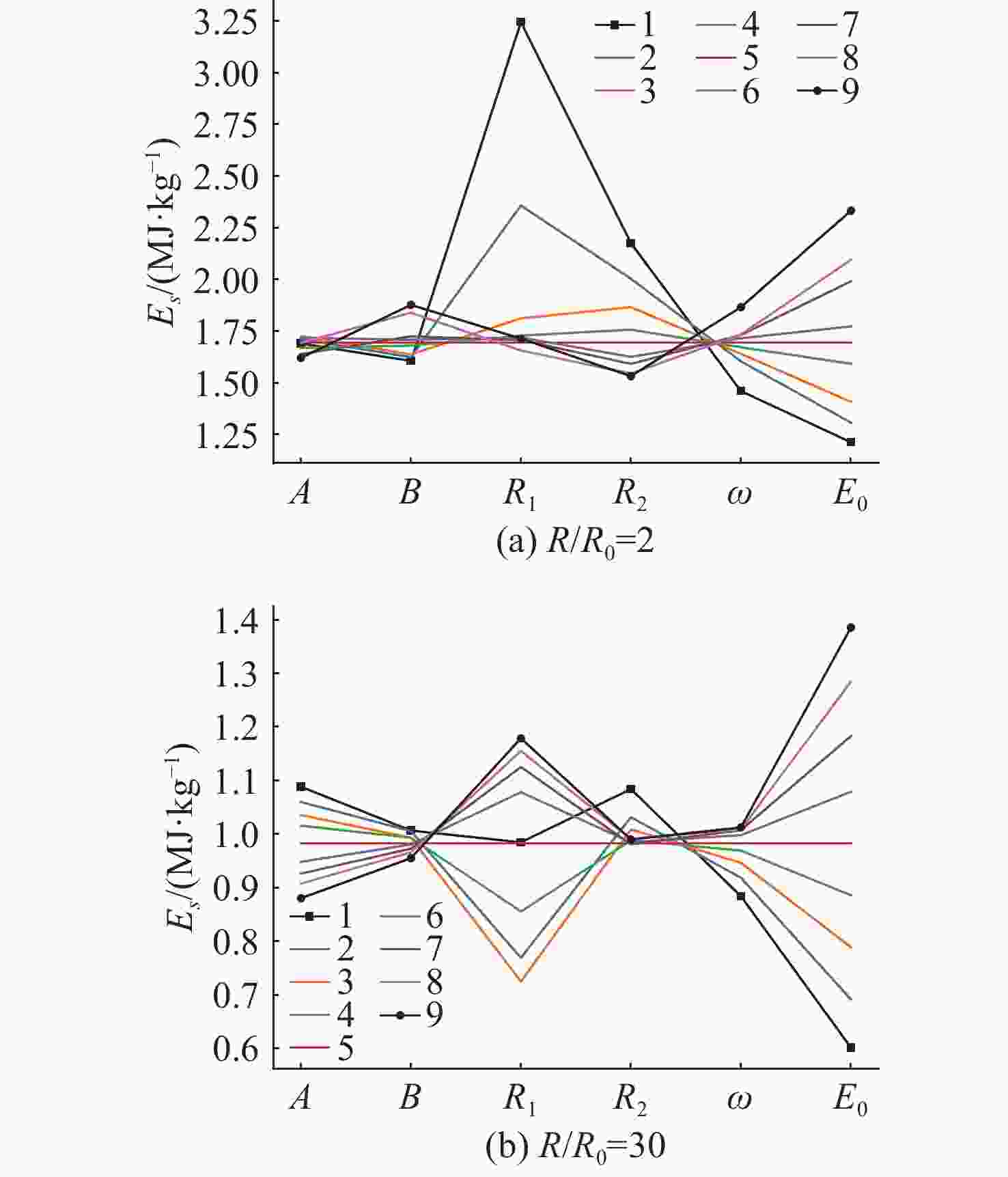
摘要: 爆轰产物状态方程是计算爆炸力学的基本方程之一, 其参数的取值变化会对数值分析结果产生直接影响。文中研究聚焦于TNT炸药JWL状态方程参数对水下爆炸冲击波数值仿真的影响, 基于LS-DYNA有限元程序, 通过与经验公式对比构建精细的一维水下爆炸数值模型, 深入分析爆轰产物JWL状态方程各参数不同取值下爆炸冲击波压力衰减规律以及能量释放等关键过程的变化规律。结果显示, JWL状态方程参数对水下爆炸冲击波峰值压力、比冲量及比冲击波能等参数均有重要影响, 且在不同爆心距离上的影响不尽相同, 在峰值压力方面, 近场范围R1影响远大于其他参数, 而中远场范围则是E0影响最大, 且峰值压力越大衰减越快; 比冲量方面E0的改变影响最大, 且改变E0时比冲量计算值与参数大小成线性关系; 比冲击波能方面同样E0影响最大。研究结果可为水下爆炸数值仿真中JWL方程参数合理取值提供参考依据。Abstract: The equation of state for detonation products is one of the fundamental equations in computational explosion mechanics, changes in the values of its parameters directly affect the results of numerical analysis. This study focuses on the influence of the parameters of the JWL equation of state for TNT explosives on the numerical simulation of underwater explosion shock waves. Based on the LS-DYNA finite element program, a refined one - dimensional numerical model of underwater explosion is constructed by comparing with empirical formulas. An in - depth analysis is conducted on the variation laws of key processes such as the pressure attenuation of explosion shock waves and energy release under different values of each parameter in the JWL equation of state for detonation products.The results show that the parameters of the JWL equation of state have significant impacts on parameters such as the peak pressure, specific impulse, and specific shock wave energy of underwater explosion shock waves, and the impacts vary at different distances from the explosion center. In terms of peak pressure, in the near field range, the influence of R1 is much greater than that of other parameters, while in the middle and far field ranges, E0 has the greatest influence. Moreover, the higher the peak pressure, the faster the attenuation. In terms of specific impulse, changes in E0 have the greatest influence, and when E0 is changed, the calculated value of specific impulse has a linear relationship with the parameter value. Similarly, E0 has the greatest influence on specific shock wave energy.
-
Key words:
- underwater explosion /
- JWL equation of state /
- numerical simulation
-
图 3 不同R/R0下归一化压力与网格尺寸关系
Figure 3. The relationship between normalized pressure and grid size under different R/R0
图 4 数值模型与经验公式峰值压力对比图
Figure 4. Comparison of Peak Pressure between Numerical Model and Empirical Formula
图 6 不同A值下峰值压力-距离曲线
Figure 6. Peak pressure-distance curves under different values of A
图 9 不同B值下峰值压力-距离曲线
Figure 9. Peak pressure-distance curves under different values of B
图 12 不同R1值下峰值压力-距离曲线
Figure 12. Peak pressure-distance curves under different values of R1
图 15 不同R2值下峰值压力-距离曲线
Figure 15. Peak pressure-distance curves under different values of R2
图 18 不同ω值下峰值压力-距离曲线
Figure 18. Peak pressure-distance curves under different values of ω
图 21 不同E0值下峰值压力-距离曲线
Figure 21. Peak pressure-distance curves under different values of E0
图 24 各参数不同取值下峰值压力变化曲线
Figure 24. Peak pressures curves under different values of each parameter
图 25 各参数不同取值下比冲量变化曲线
Figure 25. Specific impulse curves under different values of each parameter
图 26 各参数不同取值下比冲击波能变化曲线
Figure 26. Specific shock energy curves with different values of each parameter
表 1 炸药材料和JWL状态方程参数
Table 1. Material and JWL Equation of State Parameters of Explosive
参数 符号 数值 炸药密度 $ {\rho _E}/\left( {{\text{g}} \cdot {\text{c}}{{\text{m}}^{{{ - 3}}}}} \right) $ 1.63 炸药爆速 $ D/\left( {{\text{m}} \cdot {{\text{s}}^{{{ - 1}}}}} \right) $ 6 930 爆轰CJ点压力 $ {P_{{\text{CJ}}}}/{\text{GPa}} $ 21 炸药单位体积初始内能 $ {E_0}/{\text{GPa}} $ 7 JWL参数 $ A/{\text{GPa}} $ 373.77 $ B/{\text{GPa}} $ 3.747 R1 4.15 R2 0.9 $ \omega $ 0.35 
下载: 导出CSV
表 2 海水材料和Grünesien状态方程参数
Table 2. Material and Grüneisen equation of state parameters of seawater
参数 符号 数值 海水密度 $ {\rho _w}/\left( {{\text{g}} \cdot {\text{c}}{{\text{m}}^{{{ - 3}}}}} \right) $ 1.025 声速 $ C/\left( {{\text{m}} \cdot {{\text{s}}^{{{ - 1}}}}} \right) $ 1520 海水单位体积初始内能 $ {E_{w0}}{\text{/MPa}} $ 0.7 Grünesien参数 S1 1.92 S2 0 S3 0 $ {\gamma _0} $ 0.28 A 0
下载: 导出CSV
-
[1] 温丽晶, 段卓平, 张震宇, 等. 采用遗传算法确定炸药爆轰产物JWL状态方程参数[J]. 爆炸与冲击, 2013, 33(S1): 130-134.WEN L J, DUAN Z P, ZHANG Z Y, et al. Determination of the JWL EOS parameters for detonation products using genetic algorithm[J]. Explosion and Shock Waves, 2013, 33(S1): 130-134. [2] 王树山, 贾曦雨, 高源, 等. 水下爆炸动力学的起源、发展与展望[J]. 水下无人系统学报, 2023, 31(1): 10-29.WANG S S, JIA X Y, GAO Y, et al. Underwater explosion dynamics: Its origin, development, and prospect[J]. Journal of Unmanned Undersea Systems, 2023, 31(1): 10-29. [3] Cole R H. Underwater explosions[M]. Princeton, NJ, USA: Princeton University Pr. , 1948. [4] GAN N, YAO X L, LIU L T, et al. Research on overall damage characteristics of a hull girder under explosion bubble collapse[J]. Ocean Engineering, 2019, 188: 106315. doi: 10.1016/j.oceaneng.2019.106315 [5] JIN Z, YIN C, CHEN Y, et al. Dynamics of an underwater explosion bubble near a sandwich structure[J]. Journal of Fluids and Structures, 2019, 86: 247-265. doi: 10.1016/j.jfluidstructs.2019.02.022 [6] 李彬, 田恒斗, 刘文思, 等. RDX基含铝炸药JWL-Miller状态方程标定及对舰船结构的毁伤特性[J]. 火炸药学报, 2024, 47(8): 704-713.LI B, TIAN H D, LIU W S, et al. Calibration of JWL-Miller equation of state for RDX-based aluminized explosives and damage characteristics to ship structures[J]. Chinese Journal of Explosives & Propellants, 2024, 47(8): 704-713. [7] 王杰, 王景焘, 黄超, 等. 一种面向舰船结构毁伤的大变形流固耦合数值计算方法[J]. 计算力学学报, 2024, 41(2): 335-343.WANG J, WANG J T, HUANG C, et al. A numerical method for fluid-structure interaction with large deformation towards the damage of warship structures[J]. Chinese Journal of Computational Mechanics, 2024, 41(2): 335-343. [8] 陈涛, 汪海波, 王丽敏, 等. 不耦合系数对水下爆破破岩效果影响的数值分析[J]. 工程爆破, 2022, 28(6): 25-32.CHEN T, WANG H B, WANG L M, et al. Numerical analysis of the influence of decoupling coefficient on rock breaking effect of underwater blasting[J]. Engineering Blasting, 2022, 28(6): 25-32. [9] 吴亮, 余创, 梁志坚, 等. 基于Fluent-EDEM流固耦合算法的水下台阶爆破爆堆形成过程研究[J]. 爆破, 2023, 40(4): 37-43. doi: 10.3963/j.issn.1001-487X.2023.04.005WU L, YU C, LIANG Z J, et al. Study on formation process of underwater bench blasting pile based on fluid-structure coupling algorithm of Fluent-EDEM[J]. Blasting, 2023, 40(4): 37-43. doi: 10.3963/j.issn.1001-487X.2023.04.005 [10] 杜明燃, 陈宇航, 陆少锋, 等. 基于正交试验法的气泡帷幕削波特性研究[J]. 高压物理学报, 2023, 37(6): 195-205.DU M R, CHEN Y H, LU S F, et al. Bubble curtain clipping characteristics based on orthogonal test method[J]. Chinese Journal of High Pressure Physics, 2023, 37(6): 195-205. [11] 范怀斌, 陆少锋, 莫崇勋, 等. 基于ANSYS LS-DYNA水下爆破阻波帘的设计与研究[J]. 爆破, 2023, 40(2): 138-143. doi: 10.3963/j.issn.1001-487X.2023.02.020FAN H B, LU S F, MO C X, et al. Design and research of wave blocking curtain for underwater blasting based on ANSYS LS-DYNA[J]. Blasting, 2023, 40(2): 138-143. doi: 10.3963/j.issn.1001-487X.2023.02.020 [12] 徐辉, 孙占峰, 李庆忠. 标准圆筒试验数据处理和不确定度评定方法[J]. 北京理工大学学报, 2010, 30(5): 626-630.XU H, SUN Z F, LI Q Z. Data processing and uncertainty evaluation methods for standard cylinder tests[J]. Transactions of Beijing Institute of Technology, 2010, 30(5): 626-630. [13] 王言金, 张树道, 李华, 等. 炸药爆轰产物Jones-Wilkins-Lee状态方程不确定参数[J]. 物理学报, 2016, 65(10): 245-250.WANG Y J, ZHANG S D, LI H, et al. Uncertain parameters of Jones-Wilkin-Lee equation of state for detonation products of explosive[J]. Acta Physica Sinica, 2016, 65(10): 245-250. [14] 陈华, 周海兵, 刘国昭, 等. 圆筒试验JWL状态方程参数的贝叶斯标定[J]. 爆炸与冲击, 2017, 37(4): 585-590.CHEN H, ZHOU H B, LIU G Z, et al. Bayesian calibration for parameters of JWL equation-of-state parameters in cylinder tests[J]. Explosion and Shock Waves, 2017, 37(4): 585-590. [15] 刘全, 王瑞利, 林忠, 等. 爆轰计算JWL状态方程参数的不确定度[J]. 爆炸与冲击, 2013, 33(6): 647-654.LIU Q, WANG R L, LIN Z, et al. Uncertainty of JWL EOS Parameters in explosive numerical simulation[J]. Explosion and Shock Waves, 2013, 33(6): 647-654. [16] 郝礼楷, 顾文彬, 谢兴博, 等. 基于BP神经网络预测炸药JWL状态方程参数对EFP速度的影响[J]. 兵器装备工程学报, 2023, 44(6): 47-55.HAO L K, GU W B, XIE X B, et al. Prediction of the influence of parameters of JWL equation of state on EFP velocity based on BP neural network[J]. Journal of Ordnance Equipment Engineering, 2023, 44(6): 47-55. [17] 敖启源, 卢熹, 姜智雅, 等. 水下爆炸冲击波数值仿真精度研究[J]. 水下无人系统学报, 2024, 32(1): 158-165.AO Q Y, LU X, JIANG Z Y, et al. Numerical simulation accuracy study of underwater explosion shock waves[J]. Journal of Unmanned Undersea Systems, 2024, 32(1): 158-165. [18] 闫秋实, 常松. 水下爆炸三维数值模拟特征参量敏感性分析[J]. 北京工业大学学报, 2023, 49(10): 1099-1108.YAN Q S, CHANG S. Underwater explosion 3D numerical simulation characteristic parameter sensitivity analysis[J]. Journal of Beijing University of Technology, 2023, 49(10): 1099-1108. [19] 崔浩, 郭锐, 宋浦, 等. 基于遗传算法辨识炸药JWL状态方程参数的研究[J]. 振动与冲击, 2022, 41(9): 174-180, 209.CUI H, GUO R, SONG P, et al. Research on the identification of JWL equation of state parameters of explosives based on genetic algorithm[J]. Journal of Vibration and Shock, 2022, 41(9): 174-180, 209. [20] 陈兴, 周兰伟, 李福明, 等. 爆炸深度对装药水下载荷的影响[J]. 兵器装备工程学报, 2021, 42(8): 79-84. doi: 10.11809/bqzbgcxb2021.08.013CHEN X, ZHOU L W, LI F M, et al. Research on influence of depth of charge on underwater explosion load[J]. Journal of Ordnance Equipment Engineering, 2021, 42(8): 79-84. doi: 10.11809/bqzbgcxb2021.08.013 [21] ЛП奥尔连科. 爆炸物理学[M]. 孙承纬, 译. 北京: 科学出版社, 2011. [22] 徐庆涛, 马宏昊, 周章涛, 等. 基于压力-冲量曲线的水下爆炸压力-时间公式[J]. 爆炸与冲击, 2024, 44(8): 159-166.XU Q T, MA H H, ZHOU Z T, et al. Pressure-time formula for underwater explosion based on pressure-impulse curve[J]. Explosion and Shock Waves, 2024, 44(8): 159-166. [23] 李科斌, 董新龙, 李晓杰, 等. 水下爆炸实验法在工业炸药JWL状态方程测定中的应用研究[J]. 兵工学报, 2020, 41(3): 488-494.LI K B, DONG X L, LI X J, et al. Research on parameters determination of JWL EOS for commercial explosives based on underwater explosion test[J]. Acta Armamentarii, 2020, 41(3): 488-494. [24] JACKSON S I. Scaling of the detonation product state with reactant kinetic energy[J]. Combustion and Flame, 2018, 190: 240-251. doi: 10.1016/j.combustflame.2017.12.008 -
点击查看大图
计量
- 文章访问数: 3
- HTML全文浏览量: 2
- PDF下载量: 0
- 被引次数: 0
