Multi-agent Reinforcement Learning-based Transmission Scheduling with Cross-layer Design for Underwater Acoustic Networks in Time-varying Channels
-
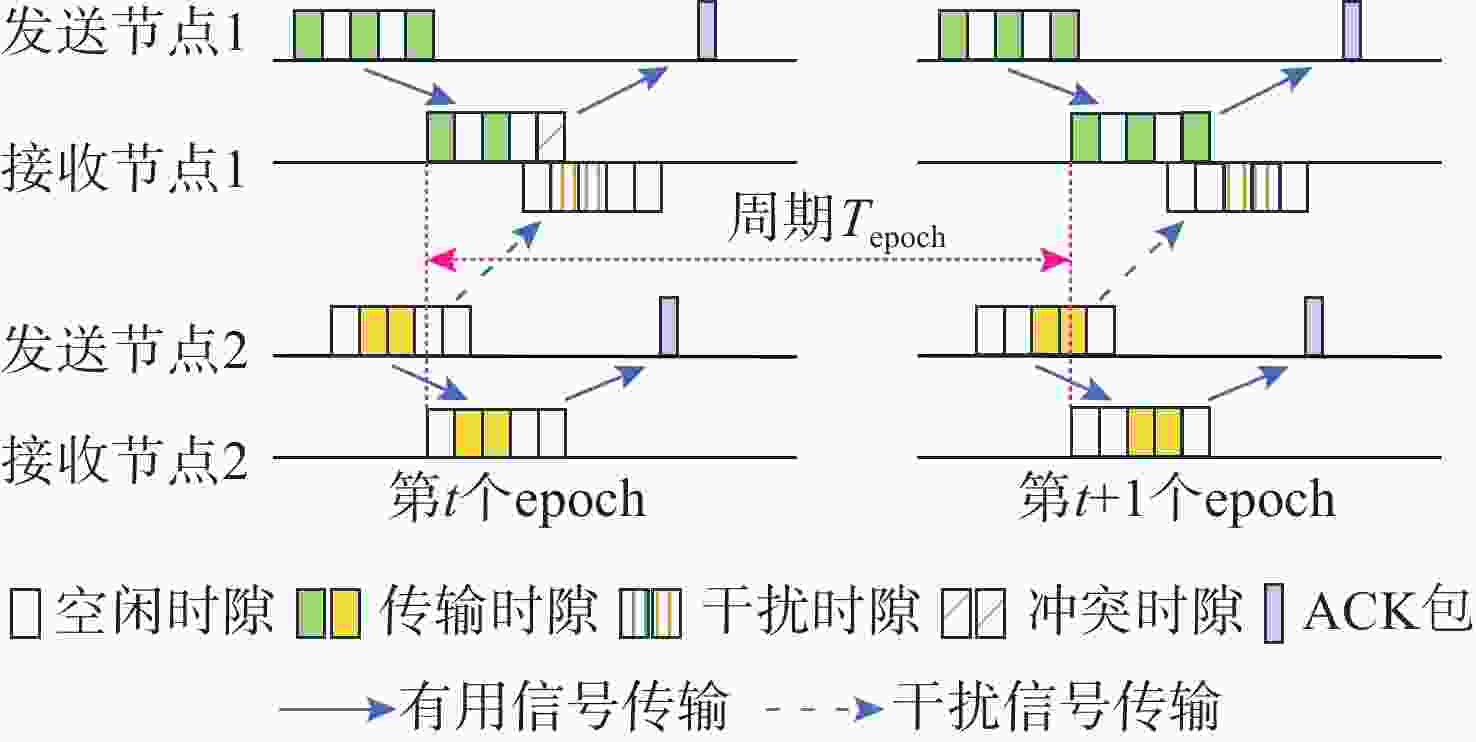
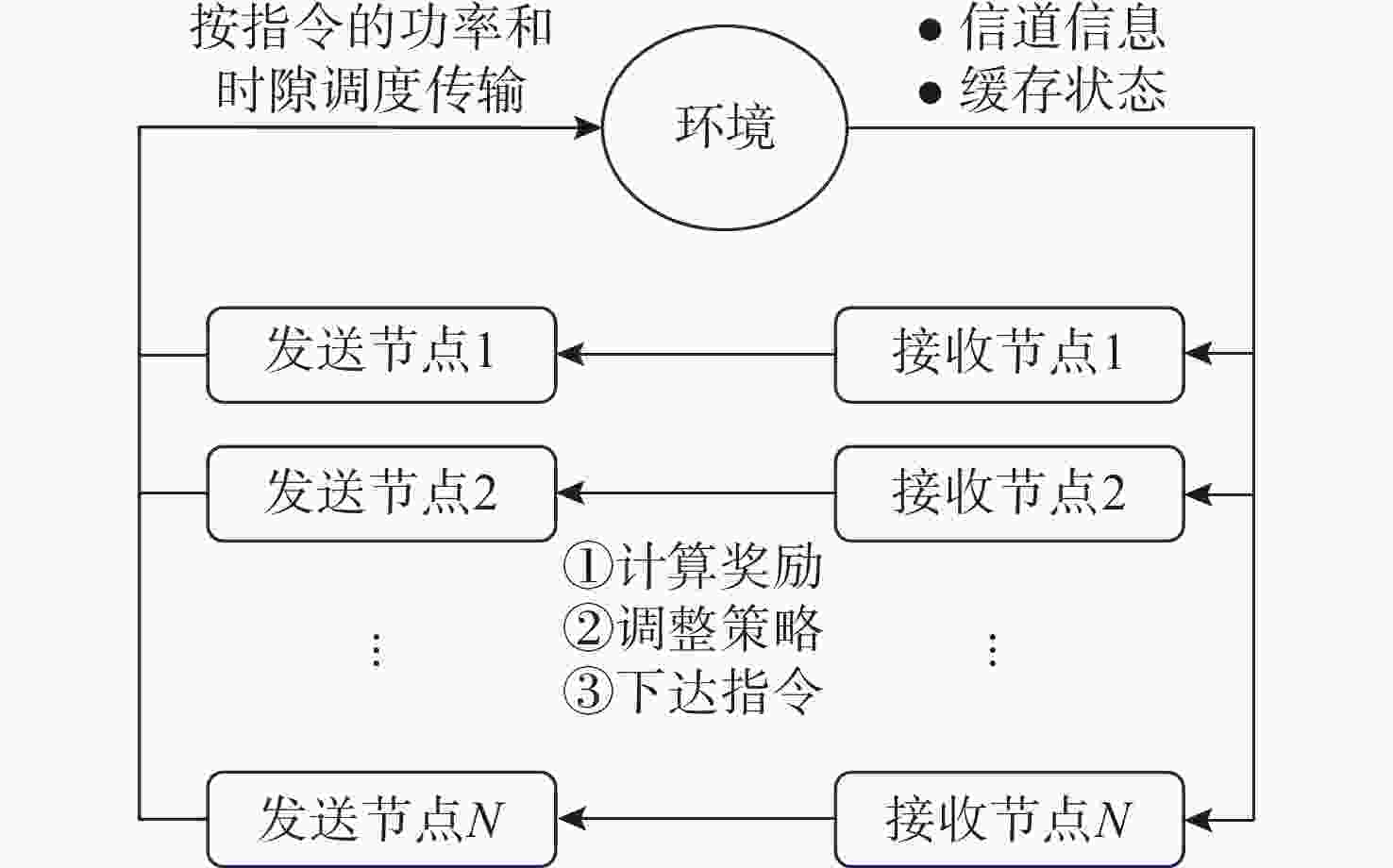
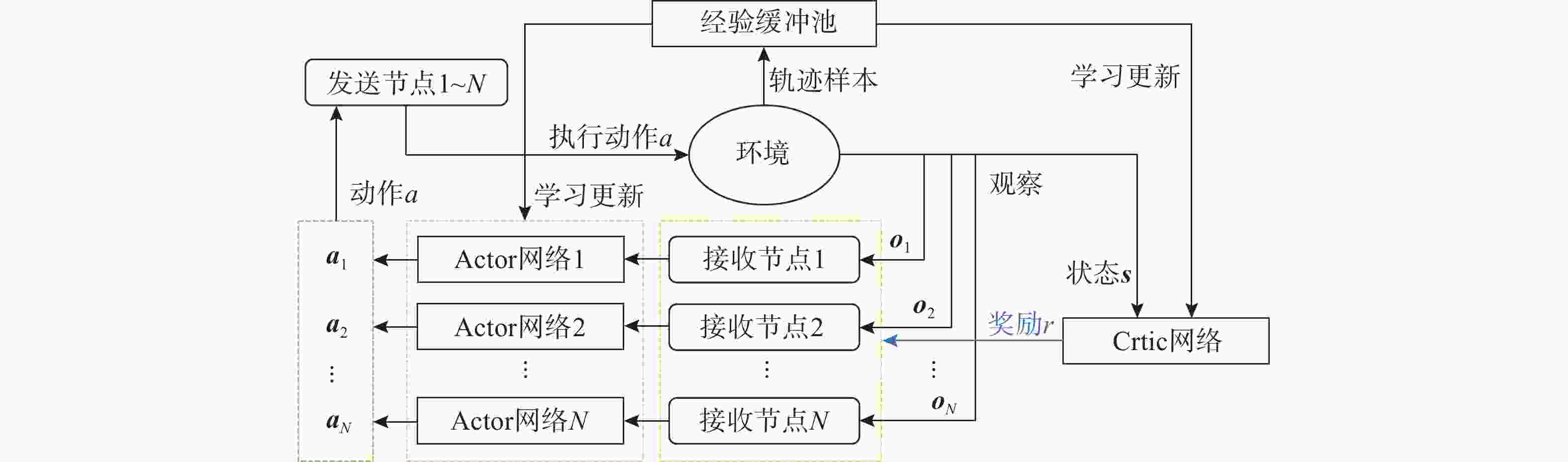
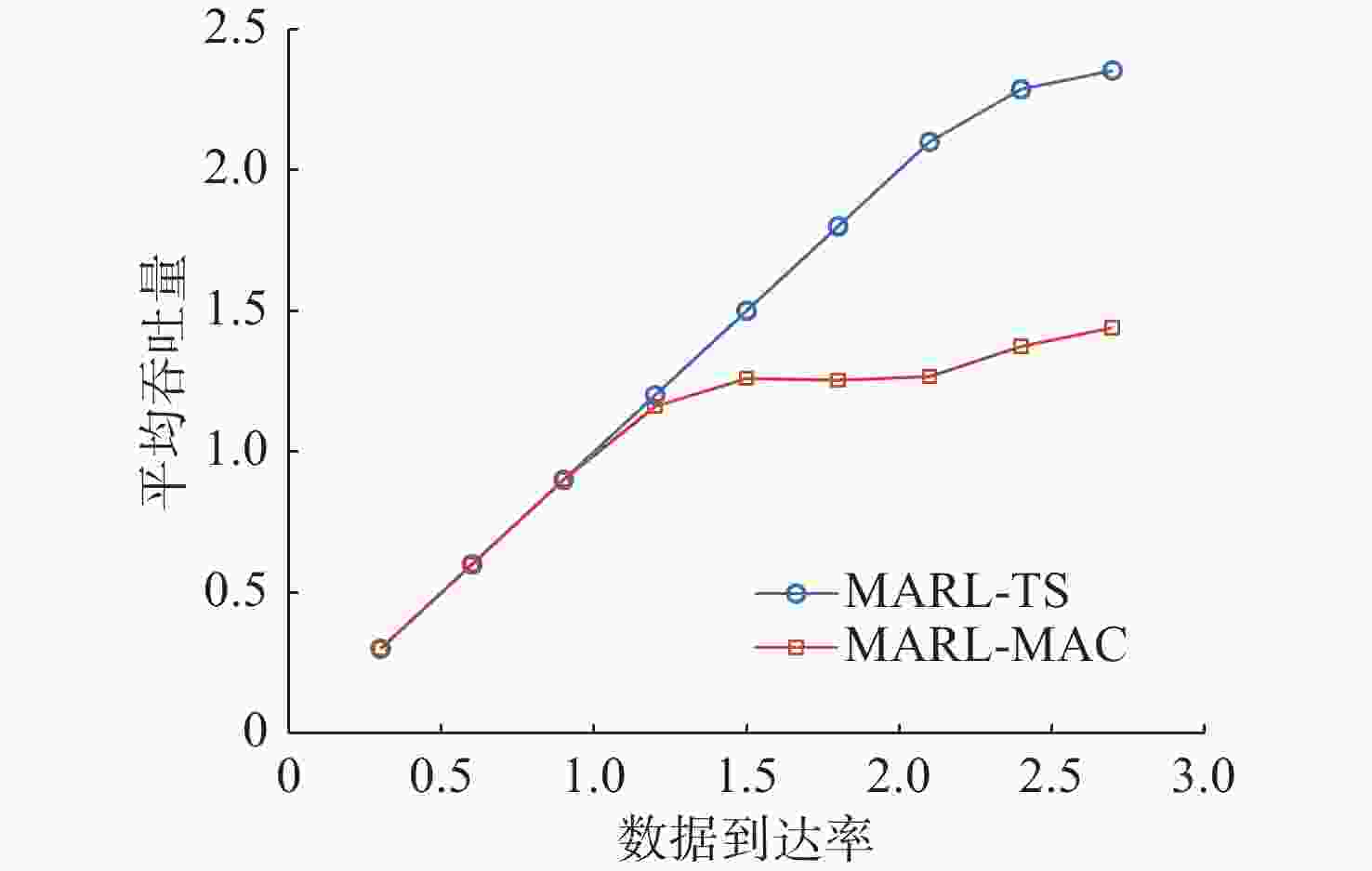
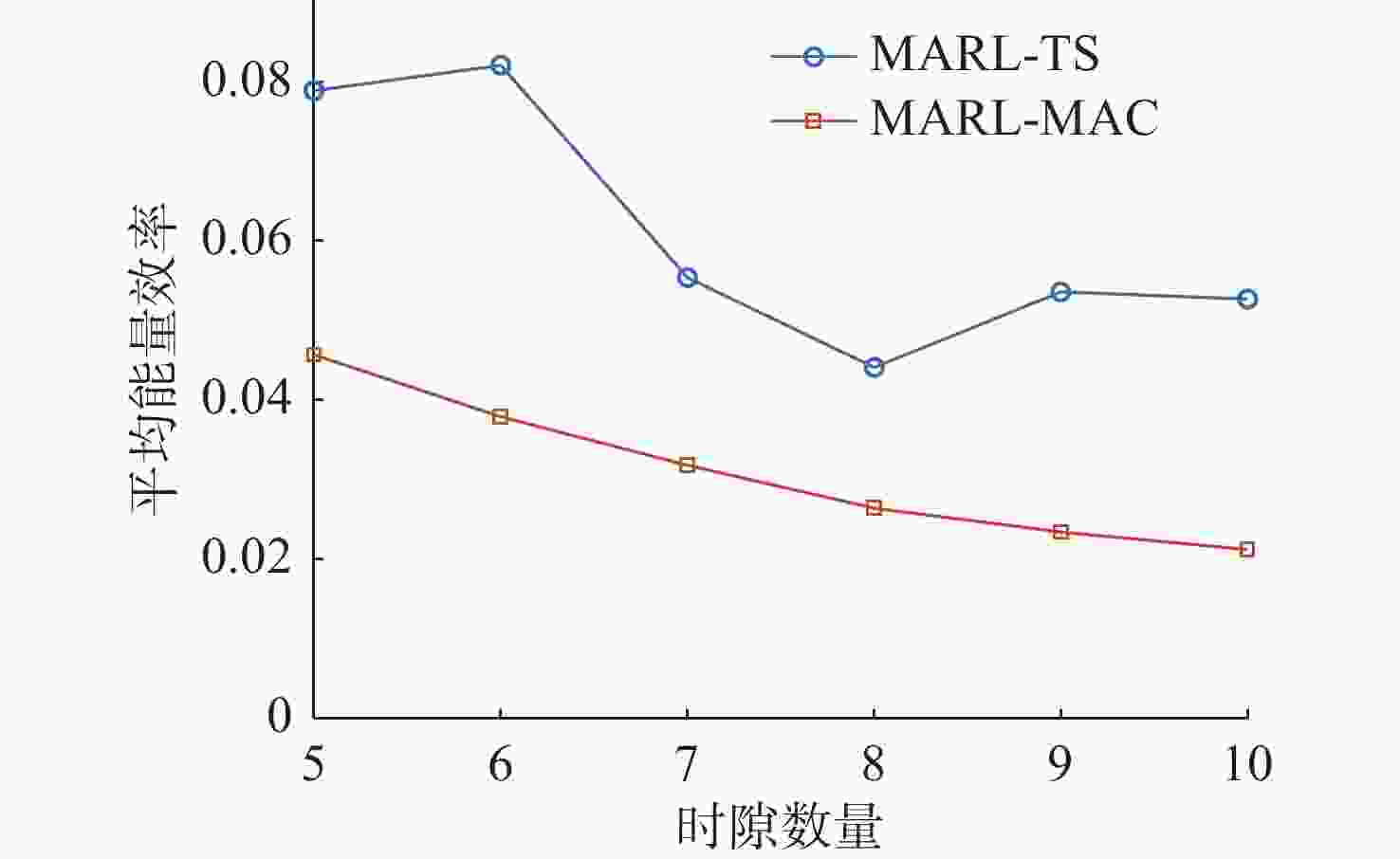
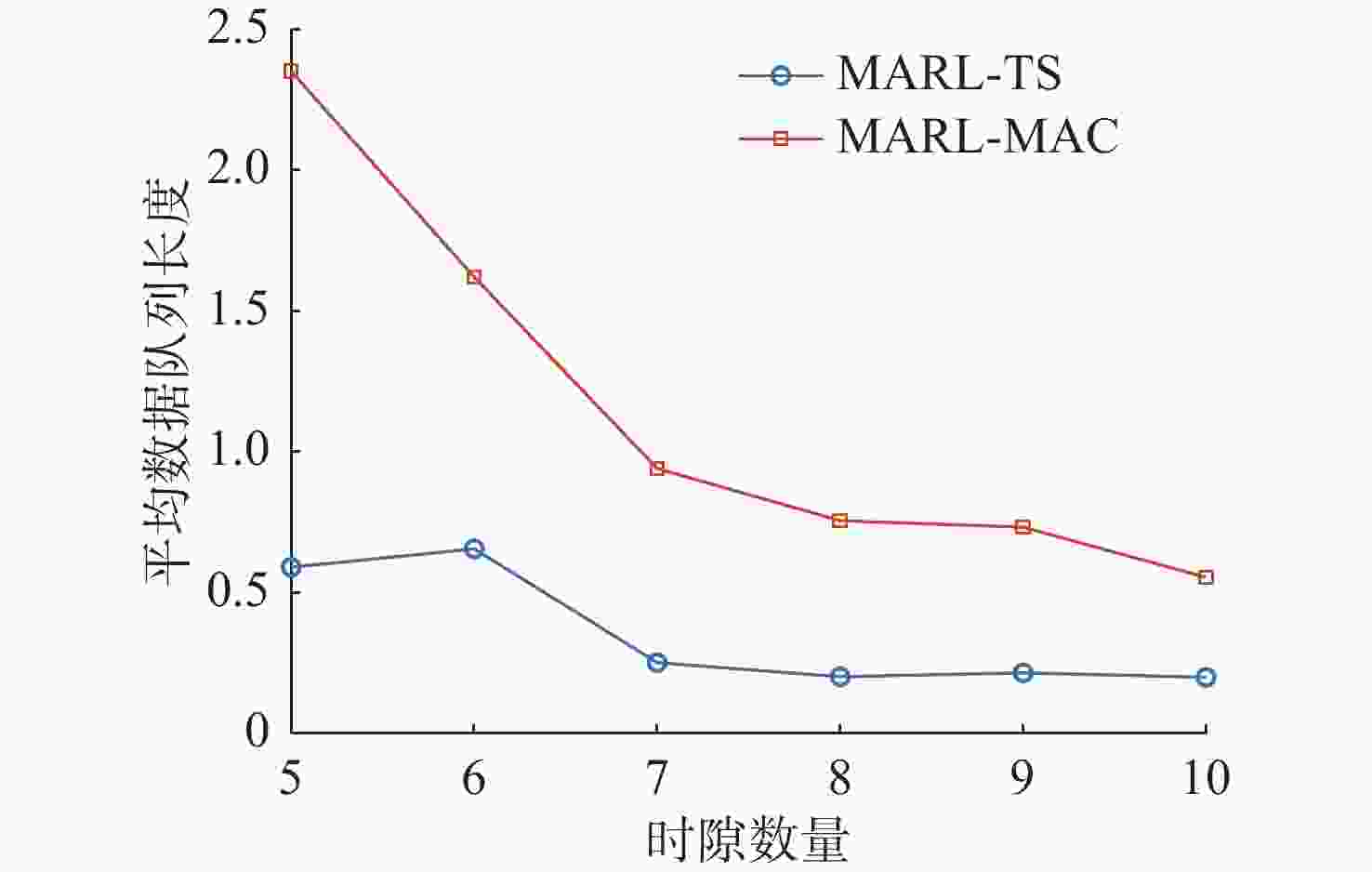
摘要: 水声通信因其高传播时延、信道时变特性及带宽受限等因素, 在传输调度决策方面面临诸多挑战。为提升复杂水声环境下的通信效率, 文中提出了一种基于多智能体强化学习(MARL)的水声网络跨层传输方法(MARL-TS)。该方法针对高水声传播时延和动态信道环境, 以传输节点的数据缓存状态与信道条件为基础, 以通信网络的传输效率和传输时延为优化目标, 自适应地进行跨层优化, 实现功率分配与时隙资源调度的联合优化。为学习最优传输策略, 文中构建了可学习的策略生成网络与价值评价网络, 并结合多智能体协同学习, 提升策略优化的效率与自适应决策能力。仿真实验表明, 与现有基于强化学习的多路访问控制(MAC)协议相比, MARL-TS在传输能效优化和传输时延降低等方面表现出显著优势, 尤其在多节点高负载场景下展现了更强的适应性与稳定性, 为复杂水下通信系统的优化提供了新的思路。Abstract: Underwater acoustic (UWA) communication faces numerous challenges in transmission scheduling and decision-making due to its high propagation delay, time-varying channel characteristics, and limited bandwidth. To enhance communication efficiency in complex UWA environments, this paper proposes a multi-agent reinforcement learning (MARL)-based cross-layer transmission method for UWA networks, termed MARL-TS. This method addresses the high propagation delay and dynamic channel conditions by leveraging transmission node buffer states and channel conditions as the foundation while optimizing network throughput and transmission delay. It adaptively performs cross-layer optimization to jointly optimize power allocation and timeslot scheduling. To learn the optimal transmission strategy, this study constructs a learnable policy generation network and a value evaluation network, integrating multi-agent cooperative learning to improve strategy optimization efficiency and adaptive decision-making capabilities. Simulation results demonstrate that, compared with existing reinforcement learning-based MAC protocols, MARL-TS significantly enhances transmission efficiency and reduces transmission delay. Notably, it exhibits superior adaptability and stability in multi-node, high-load scenarios, offering a novel approach for optimizing complex underwater communication systems.
-
0. 引言
地球表面约 71% 为水体所覆盖, 在这样广袤的水域环境中, 水下无人系统于水下资源开发、环境监测、国防安全以及科学探索等诸多领域均发挥着至关重要的作用[1]。在水下通信领域, 电磁信号在水中会经历极为迅速的衰减过程, 这极大地限制了其在水下通信中的应用[2]。与之形成对比的是, 声波在水中传播时, 损耗相对处于较低水平, 能够实现中远距离的数据传输。因此, 水声通信成为水下无人系统进行中远距离信息传输的最为有效方式[3]。近年来, 随着水下开发需求的增长, 水下物联网这一新兴技术受到广泛关注[4]。在特定区域, 水下物联网利用多节点水声通信网络, 为更多水下无人设备提供服务, 不仅扩展网络覆盖范围, 还满足高可靠性和低延迟的需求[5]。然而, 由于多链路通信共存, 如何调度传输以减少干扰和冲突是亟待解决的挑战[6][7]。
此外, 水声通信面临着其自身固有的诸多挑战。在传播特性方面, 声波在水中的传播速度约为1 500 m/s, 与电磁波速度相比相差显著, 由此引发的信号传播延迟问题不容忽视。这一特性导致传统无线网络中广泛使用的介质访问控制(medium access control, MAC)协议及相关设计策略难以直接适用于水声通信场景[8]。高传播延迟进一步引发了水声通信中的时空不确定性: 声信号的到达时间不仅取决于发送时刻, 还受到发送端与接收端之间距离的显著影响。这一特点无疑加剧了在复杂水下干扰环境中实现高效传输调度的难度[9]。此外, 水声信道具有高度动态性, 其特性会随着时间和环境条件的变化而波动。例如, 水流、温度梯度以及水面运动等多种因素均会对信道产生显著影响, 从而导致信号质量的不稳定性和通信连接的间歇性特征[10]。在能源受限的水下环境中, 基于通信质量自适应调整功率可以有效减少通信资源浪费和能耗, 确保水下无人系统构建的水声通信网络能够长期、稳定且高效地运行。
针对高水声传播延迟及其引发的时空不确定性, Zhao等[6]在MAC层进行传输调度, 尽可能在时域对齐接收干扰, 以增加可用传输时隙。此外, 研究[11]、[12]将传输调度问题建模为在线动作决策问题, 基于强化学习(reinforcement learning, RL)利用传输调度反馈, 动态学习最优策略, 以应对时空不确定性。Huang等[13]研究了水声通信网络中多个发射器和接收器共存的功率管理问题, 并基于非合作博弈建模, 实现了动态环境下的最优传输策略。该方法优化了网络传输速率和能效, 同时延长了发射器的寿命。Ye等[14]设提出了一种基于深度强化学习(reinforcement learning, RL)的MAC协议, 将每个时隙的传输决策作为动作, 优化网络吞吐量, 并在异构 MAC 协议环境下, 实现单节点的高效传输。Huang等[15]提出了一种适用于水声多簇网络的分布式协议, 通过结合历史信息辅助与奖励优化机制, 缓解传播延迟带来的不确定性问题。该方法在提高吞吐量和资源利用率的同时, 有效降低了通信开销和碰撞概率。然而, 上述方法均基于MAC层设计, 假设水声传播延迟为整数倍时隙长度, 且并未考虑物理层复杂的水声信道变化, 因此难以适应真实场景中任意传播延迟的情况, 也无法针对信道变化优化传输能效, 从而提升水下通信效率。Wang等[16]针对点对点网络, 在时变水声信道环境下, 基于RL自适应调节物理层参数, 提高网络吞吐量, 并通过减少数据缓存量有效降低信息传输时延。然而, 该方法难以直接扩展至多节点水声网络, 且未考虑时隙调度对能耗优化的作用。
文中基于多智能体强化学习(multi-agent reinforcement learning, MARL)针对多节点水声通信网络, 考虑任意水声传播延迟的通用场景, 提出了一种基于时变水声信道跨层自适应调整传输参数(包含传输功率与传输时隙)的方法(MARL-based transmission scheduling, MARL-TS)。主要贡献包括: 1)针对高传播延迟和时变水声信道的特点, 设计了一种适应复杂水声环境的传输模式; 2)提出基于在线学习的联合传输调度与功率分配方法, 实现资源利用率与通信性能的动态优化; 3)与现有强化学习驱动的 MAC 协议相比, 该方法显著提升传输能效, 并有效降低信息传输延迟。
1. 系统模型
文中研究水下物联网场景, 其中多个水下传感器需将信息及时传输至水面。为增强信息传输的实时性和可靠性, 系统采用多个浮标作为接收节点, 以扩展通信覆盖范围并提供稳定服务[15]。此外, 在文中研究的无人系统中, 接收节点与传感器采用一对一配对方式, 以优化通信资源利用率, 提高水下信息传输效率, 实现高可靠及低延迟的数据传输[17]。如图1所示, 接收节点为漂浮在水面的浮标, 其利用水声通信与水下节点进行信息传输, 并可通过高速无线电链路将收集的信息发送至陆地数据中心。作为发送节点, 各传感器通过从环境中收集数据进行感知, 并配备有数据缓冲区, 用于存储未被成功发送的信号包。此外, 未被接收解码的信号会保留在数据缓冲区中, 等待后续重新传输。数据缓存量越多, 则信息传输时延就会越高, 造成网络的阻塞。每个接收唯一对应一个传发送节点, 形成一对一的通信关系, 以保证传感器节点数据的高效传输。当然, 由于其他未配对的发送节点的存在, 接收不可避免地受到其干扰, 从而对通信传输效率产生影响。此外, 各接收节点可通过中心节点进行信息共享和集中训练。
图2展示了系统时间上的运行模式, 即系统由时期(epoch)组成, 每个时期由一定数量的时隙组成。针对水下无人系统供能受限的场景, 文中考虑发送节点周期性唤醒, 各时期之间非连续排列, 存在固定的时间
$ {T_{{\text{epoch}}}} $ 。此外, 考虑时隙与待传输的信号包长度一致, 各发送节点在每个时隙可传输单个信号包。在本系统中, 由于各接收节点与中心节点相连, 可进行快速信息分享, 故各接收节点可精确时钟同步, 所以可调整各发送节点时期的开始时间, 以实现各节点信号接收的同步。由于各干扰链路的距离不同, 导致信号传播延时不同, 因此, 来自其他发送节点的干扰信号并不完全与有用信号对齐, 导致接收的有用信号与干扰信号产生干扰重叠。这种部分重叠导致不同时隙中的干扰水平不同, 具体取决于干扰信号的相对时间和传播延迟。在接收节点完成所有有用信号的解码以后, ACK包将会反馈给发送节点, 包含信道信息与信号包是否解码成功的信息。
1.1 信号传输接收模型
令
$\mathcal{N}$ 和$\mathcal{R}$ 分别为发送节点和接收节点的集合, 其中两个集合的节点个数相等($\left| \mathcal{N} \right| = \left| \mathcal{R} \right| = N$ )。文中考虑每个发送节点传输有用信息至唯一对应的接收节点, 并假设这种一一对应关系是作为先验知识已知的。为不失一般性, 发送节点i与接收节点i两两配对进行有用信号的传输。发送节点i传输的第$ {\ell _i} $ 个信号包在接收节点j处的到达时间(time of arrival, ToA)为$$ \kappa _{ij}^{({\ell _i})} = T_i^{({\ell _i})} + {\tau _{ij}} $$ (1) 式中:
$ T_i^{(\ell )} $ 为发送节点i的第$\ell $ 个信号包的传输开始时间;${\tau _{ij}}$ 为发送节点i与接收节点j之间的信号传播延迟。对于非配对的发送节点k与接收节点i(即$k \ne i$ ), 从发送节点k传输的信号包将对接收节点i产生干扰。干扰节点k传输的第$ {\ell _k} $ 个干扰信号包在接收节点i处的ToA, 其可通过式(2)计算$$ \kappa _{ki}^{\left( {{\ell _k}} \right)} = T_k^{\left( {{\ell _k}} \right)} + {\tau _{ki}} $$ (2) 则发送节点i的第
${\ell _i}$ 个信号包与干扰节点k的第${\ell _k}$ 个干扰信号包在接收节点j处的ToA差为$$ \Delta _{ikj}^{\left( {{\ell _i},{\ell _k}} \right)} = \kappa _{ij}^{\left( {{\ell _i}} \right)} - \kappa _{kj}^{\left( {{\ell _k}} \right)} $$ (3) 若式(3)中
$i = j$ , 则$ \Delta _{iki}^{\left( {{\ell _i},{\ell _k}} \right)} $ 为发送节点i传输的信号包在其配对的接收节点i上与其他干扰信号包的时间到达差。因此, 时域中的干扰模式可由ToA差$ \Delta _{iki}^{\left( {{\ell _i},{\ell _k}} \right)} $ 和信号包的持续时间${T_{{\text{block}}}}$ 表示决定:$ \left| {\Delta _{iki}^{\left( {{\ell _i},{\ell _k}} \right)}} \right| < {T_{{\text{block}}}} $ 为发送节点i的第${\ell _i}$ 个信号包在接收节点i处受到干扰节点k的第${\ell _k}$ 个信号包的干扰;$ \left| {\Delta _{iki}^{\left( {{\ell _i},{\ell _k}} \right)}} \right| \geqslant {T_{{\text{block}}}} $ 为两个信号包完全分离, 有用信号未受到干扰。1.2 信道模型
基于文献[18]、[19], 文中考虑水声信道增益同时受到空间与时间的影响。首先, 第t个时期内, 信道随时间变化的增益可由如下概率分布描述
$$ \begin{align} & {f_G}\left[ {x;m(t),\mu (t),\sigma (t)} \right] = \\ &\quad\int_0^\infty {\frac{{{x^{m(t) - 1}}\exp \left( { - \frac{{m(t)x}}{y}} \right)}}{{\Gamma (m(t))}}{{\left( {\frac{{m(t)}}{y}} \right)}^{m(t)}}} {\mkern 1mu} \\ &\quad\frac{1}{{\sqrt {2\pi } \sigma (t)y}}\exp \left\{ { - \frac{{{{\left( {\ln y - \mu (t)} \right)}^2}}}{{2\sigma {{(t)}^2}}}} \right\}dy \\ \end{align} $$ (4) 式中:
$ \Gamma ( \cdot ) $ 为Gamma函数; m为Nakagami衰减参数;$ \mu $ 和$ \sigma $ 分别为描述对数正态遮蔽的均值与标准差。定义通信链路l在第t个时期信道状态为$$ {{\boldsymbol{c}}_l}(t) = [{\mu _l}(t),{\sigma _l}(t),{m_l}(t)] $$ (5) 则在第t个时期时的通信链路l上, 第
$\ell $ 个信号包的信道随时间变化的增益${G_{l\ell }}(t)$ 可由分布$ {f_G}\left[ {x;{{\boldsymbol{c}}_l}(t)} \right] $ 描述。根据文献[20], 各通信链路上的信道参数随时间变化可以用一阶马尔可夫链表示$$ {{\boldsymbol{c}}_l}(t) = {{\boldsymbol{A}}_l} \cdot {{\boldsymbol{c}}_l}(t - 1) + {{\boldsymbol{n}}_l}(t) $$ (6) 式中:
$ {{\boldsymbol{A}}_l} $ 为捕捉信道参数动态的转移矩阵;$ {{\boldsymbol{n}}_l}(t) $ 为随机波动的噪声向量。该模型允许$ {{\boldsymbol{c}}_l}(t) $ 中的每个参数基于其先前状态及随机噪声的影响进行演化, 从而有效地表征信道条件的时间变化特性。此外, 信道还因传输距离呈现衰减
$$ L = \frac{{{h_0}}}{{{d^\beta }}} \cdot \exp \left( { - \alpha d} \right) $$ (7) 式中: d为发送节点与接收节点之间的距离;
${h_0}$ 为归一化常数;$\beta $ 为路径损耗指数;$\alpha $ 为依赖于介质和信号频率的吸收系数。最终, 考虑时空影响的信道可建模为
$$ h_l^{(\ell )}(t) = {G_{l\ell }}(t){L_l} $$ (8) 式中,
$ {L_l} $ 描述的是通信链路l上的信道随距离的衰减。如果通信链路l由发送节点i与接收节点j组成, 则信道$ h_l^{(\ell )}(t) $ 可以进一步由$ h_{ij}^{(\ell )}(t) $ 表示。1.3 信号解码模型
基于式(8)中的考虑时空影响的信道, 发送节点i的第
${\ell _i}$ 个信号包在接收节点j处的接收功率为$$ P_{{\text{rx}},ij}^{({\ell _i})}(t) = P_{{\text{tx}},i}^{({\ell _i})}(t) \cdot h_{ij}^{({\ell _i})}(t) $$ (9) 式中,
$P_{{\text{tx}},i}^{({\ell _i})}(t)$ 为发送功率。令
$ \lambda _i^{(\ell )}(t) $ 为发送节点i的第$\ell $ 个信号包在其配对的接收节点i处的信干噪比(signal-to-interference-and-noise ratio, SINR)。对于单信号包处理和正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)系统, SINR 计算为$$ \begin{gathered} \lambda _i^{(\ell )}(t) = \\ \frac{{P_{{\text{rx}},ii}^{(\ell )}(t)}}{{{N_0}B + \dfrac{1}{{{T_{{\text{block}}}}}}\displaystyle \sum\limits_{m = 1}^{{N_{{\text{block}}}}} {\displaystyle \sum\limits_{k \ne i} {P_{{\text{rx}},ki}^{(m)}} } (t){{\left[ {{T_{{\text{block}}}} - \Delta _{iki}^{(\ell ,m)}} \right]}^ + }}} \\ \end{gathered} $$ (10) 式中:
${N_0}$ 为噪声功率; B为传输带宽;${N_{{\text{block}}}}$ 为每个时期中的时隙数。${\left[ \cdot \right]^ + } = \max \{ \cdot ,0\} $ 。第$\ell $ 个信号包的干扰信号由所有非对应的发送节点的信号包贡献。文中考虑根据有用信号块的接收SINR是否 超过解码阈值
${\lambda _{{\text{th}}}}$ 来决定该次链路传输是否传输成功。定义$S_i^\ell (t)$ 为接收节点i在时间t的第$\ell $ 个信号块的传输是否成功的指示函数$$ S_i^\ell (t) = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\text{if }}\lambda _i^\ell (t) \geqslant {\lambda _{{\text{th}}}},} \\ {0,}&{{\text{otherwise}}{\text{.}}} \end{array}} \right. $$ (11) 在时间t成功传输的总信号包数
${S_i}(t)$ 通过以下获得$$ {S_i}(t) = \sum\limits_{\ell = 1}^{{N_{{\text{block}}}}} {S_i^\ell (t)} $$ (12) 对于发送节点i, 数据缓存量在第t个时期期间的变化
$$ {Q_i}(t + 1) = {Q_i}(t) + {I_i}(t) - {S_i}(t) $$ (13) 式中:
$ {Q_i}(t + 1) $ 为发送节点i在第$ t + 1 $ 个时期开始时的数据缓存量;$ {Q_i}(t) $ 为第t个时期开始时的数据缓存量;$ {I_i}(t) $ 为第t个时期期间流入数据缓存的信号包数量。当信号传输失败时, 该信号将保留在数据缓存中以供后续时期重新传输。1.4 问题陈述
文中构建的系统目标是提高网络吞吐量、增强能量效率并减少传输延迟。然而, 实现这些目标面临诸多挑战, 例如水声信道的高度动态性需要在多个目标间进行综合优化以及问题本身的序贯决策属性。传统优化方法(如遗传算法)虽然能够解决多智能体问题, 但通常更适用于静态环境。而RL提供了一种强有力的替代方案, 能够在动态环境中自动提取特征并做出智能决策。特别是在涉及多个协作智能体的系统中, MARL成为更为自然的选择。MARL不仅能够高效应对问题的动态性和分布式特性, 还能为吞吐量和能量管理的联合优化提供鲁棒的解决方案。基于此, 文中将问题建模为马尔可夫决策过程(Markov decision process, MDP)进行求解。
2. MARL-TS协议
2.1 MARL要素
通过多个智能体在共享环境中的交互, 利用MARL实现协同学习, 以优化系统整体收益。图3 展示了 MARL 的基本框架, 其具体传输与学习步骤如下: 首先, 接收节点决定发送节点的传输时隙和功率分配, 并下发指令给发送节点执行。随后, 发送节点根据指令进行数据传输。然而, 由于外部环境的影响, 不同节点的传输效果可能存在差异。接收节点根据接收到的信号估计水声信道状态, 并监测数据缓存状态的变化, 从而计算相应的奖励值。最终, 接收节点依据不同状态和动作下获得的奖励, 不断调整传输时隙与功率分配策略, 以优化传输性能。
图 3 MARL-TS协议中多智能体与环境交互示意图Figure 3. Schematic diagram of the interaction between multiple agents and the environment in the MARL-TS protocol文中考虑的各MARL要素如下:
智能体: 文中将每个接收节点视为一个智能体, 每个智能体在每个时期中独立做出决策。
动作: 智能体i在第t个时期的动作为
$$ {{\boldsymbol{a}}_i}(t) = [{a_{i1}}(t),{a_{i2}}(t), \cdots ,{a_{iN}}(t)] $$ (14) 式中, 每个元素
${a_{ij}}(t)$ 为第j个时隙的具体动作。假设${P_{{\text{max}}}}$ 为传输功率的上界。如果$0 < {a_{ij}}(t) \leqslant {P_{{\text{max}}}}$ , 表示发送节点以${a_{ij}}(t)$ 的功率传输; 如果${a_{ij}}(t) = 0$ , 表示该时隙节点空闲, 传输功率为0。观察: 在第t个时期时, 智能体i可以获取其个体观测值
$$ {{\boldsymbol{o}}_i}(t) = \left[ {{{\text{Q}}_i}(t),{{\boldsymbol{c}}_{i1}}(t),{{\boldsymbol{c}}_{i2}}(t), \cdots ,{{\boldsymbol{c}}_{iN}}(t)} \right] $$ (15) 式中, 数据缓存量
$ {{\text{Q}}_i}(t) $ 的演化见式(12),$ \{ {{\boldsymbol{c}}_{i1}}(t), {{\boldsymbol{c}}_{i2}}(t), \cdots ,{{\boldsymbol{c}}_{iN}}(t)\} $ 为描述智能体i与所有发送节点间的有用信道和干扰信道共N个信道的参数。状态: 在第t个时期时, 环境状态
${\boldsymbol{s}}(t)$ 由所有智能体的观测值组成$$ {\boldsymbol{s}}({{t}}) = \left[ {{{\boldsymbol{o}}_1}(t),{{\boldsymbol{o}}_2}(t), \cdots ,{{\boldsymbol{o}}_N}(t)} \right] $$ (16) 奖励: 文中采用了各智能体协同合作的策略, 即所有智能体共享一个共同的奖励信号。通过这种方式, 系统鼓励智能体之间的协作, 推动它们共同努力以实现全局目标的优化。对于第t个时期, 共享奖励定义为
$$ r(t) = {w_1} \cdot \displaystyle \sum\limits_{i = 1}^N {{S_i}(t)} + {w_2} \cdot \frac{{\displaystyle \sum\limits_{i = 1}^N {{S_i}(t)} }}{{{E_{{\text{total}}}}(t)}} $$ (17) 式中:
$ {S_i}(t) $ 为第i个智能体成功传输的信号包数量;$ \displaystyle \sum {{S_i}(t)} $ 为所有智能体成功传输的信号包总数;${E_{{\text{total}}}}(t)$ 为第t个时期期间所有智能体消耗的总能量; 权重${w_1}$ 和${w_2}$ 分别用于平衡数据缓存与能耗两项的贡献。2.2 MARL-TS算法框架
图4为文中的MARL-TS算法的框架示意图。文中采用一种演员-评论家(Actor-Critic)的方法, 其一般工作流程是: 在每个时间步t中, 每个智能体根据式(14)所描述的局部观察, 基于策略网络(即 Actor 网络)
$ \pi $ 来决定传输动作, 即$ {{\boldsymbol{a}}_i}(t) = \pi ({{\boldsymbol{o}}_i}(t)) $ 。所有智能体的联合动作$\{ {{\boldsymbol{a}}_1}(t), \cdots ,{{\boldsymbol{a}}_N}(t)\} $ 经由发送节点作用于环境, 环境返回奖励$ r(t) $ 和下一步全局状态${\boldsymbol{s}}(t + 1)$ 。这些转移信息$\{ {\boldsymbol{s}}(t),\{ {{\boldsymbol{a}}_1}(t), \cdots ,{{\boldsymbol{a}}_N}(t)\} ,r(t), {\boldsymbol{s}}(t + 1)\} $ 被存储到经验回放区$ \mathcal{D} $ 中, 以供后续训练使用。Actor 网络
$\pi $ 部署在接收节点处, 依据当前系统状态生成传输参数。在不指定某个智能体的一般情况下, Actor 网络采用神经网络实现, 其输入为系统状态, 输出为相应的传输时隙与传输功率$$ {\boldsymbol{a}}(t) = {\pi _\theta }\left( {{\boldsymbol{s}}(t)} \right) $$ (18) 式中,
$\theta $ 为神经网络的学习权重参数。为了优化策略, 系统从经验回放区
$ \mathcal{D} $ 中随机采样一组状态—动作轨迹$$ {\boldsymbol{\xi }} = \left[ {{\boldsymbol{s}}(0),{\boldsymbol{a}}(0),{\boldsymbol{s}}(1),{\boldsymbol{a}}(1),\cdots,{\boldsymbol{s}}(T),{\boldsymbol{a}}(T)} \right] , $$ (19) 并基于该轨迹计算折扣累计奖励
$$ R({\boldsymbol{\xi }}) = \sum\limits_{t = 0}^T {{\gamma ^t}} r({\boldsymbol{s}}(t),{\boldsymbol{a}}(t)) $$ (20) 然后, 系统的期望奖励
$J(\theta )$ 表示在当前Actor网络${\pi _\theta }$ 下, 智能体从初始状态开始, 基于Actor网络历史生成动作$ \{ {\boldsymbol{a}}(t)\} _{t = 0}^\infty $ 与环境交互所累积奖励的期望值。为了优化 Actor 网络的策略, 使其生成更优的传输参数, 可以通过最大化以下目标函数来优化策略$$ J(\theta ) = {\mathbb{E}_{{\boldsymbol{\xi }}\sim {\pi _\theta }}}\left[ {R({\boldsymbol{\xi }})} \right] $$ (21) 基于策略梯度定理, Actor 网络的参数更新规则为
$$ \theta ' = \theta + {\omega _\theta }{\nabla _\theta }J(\theta ) $$ (22) 式中,
$ {\omega _\theta } $ 为学习率。通过这一优化过程, Actor 网络逐步提高选择最优策略的概率, 从而提升系统的传输收益。基于采样的轨迹, 期望奖励可进一步展开为
$$ J(\theta ) = \sum\limits_{t = 0}^T {\log {\pi _\theta }({\boldsymbol{a}}(t)|{\boldsymbol{s}}(t)) \cdot \delta (t)} $$ (23) 式中,
${\pi _\theta }({\boldsymbol{a}}(t)|{\boldsymbol{s}}(t))$ 为${\pi _\theta }$ 基于${\boldsymbol{s}}(t)$ 状态下生成${\boldsymbol{a}}(t)$ 的概率。时序差分误差可通过式(23)计算$$ \delta (t) = r(t) + {V^\pi }({\boldsymbol{s}}(t + 1)) - {V^\pi }({\boldsymbol{s}}(t)) $$ (24) 式中,
${V^\pi }({\boldsymbol{s}}(t))$ 为智能体在Actor网络$\pi $ 下给定状态的价值函数。该函数反映了从状态${\boldsymbol{s}}(t)$ 开始, 采取基于$\pi $ 生成的后续动作, 其未来能够获得的期望收益。$\delta (t)$ 衡量了在状态${\boldsymbol{s}}(t)$ 下选择动作${\boldsymbol{a}}(t)$ 所获得的收益相较于下一状态的平均收益的提升程度, 从而指导 Actor 网络优化传输参数。通常, 价值函数
${V^\pi }$ 由可由神经网络${V_\phi }$ (即Critic网络)表示, 其中$\phi $ 为神经网络的学习权重参数。在传输过程中, Critic 网络需要不断学习, 以提高其对平均收益的估计精度。本质上, Critic 网络可用于评估某一状态-动作对的优劣, 其优化目标为$$ \phi ' = \phi - {\omega _\phi }{\nabla _\phi }{J_V}(\phi ) $$ (25) 式中:
$ {\omega _\phi } $ 为学习率;$ {J_V}(\phi ) = {{{{\left[ {\delta (t)} \right]}^2}} \mathord{\left/ {\vphantom {{{{\left[ {\delta (t)} \right]}^2}} 2}} \right. } 2} $ 为优化目标。该优化过程减少了基于即时奖励估计的平均收益$r(t) + {V_\phi }({\boldsymbol{s}}(t + 1))$ 与理论收益${V_\phi }({\boldsymbol{s}}(t))$ 之间的差异, 从而提升 Critic 网络的价值估计能力, 并辅助 Actor 网络更高效地优化策略。文中所提出的MARL-TS在Actor-Critic的基础上采用MAPPO算法[21-22]进行策略网络的更新, 其核心是在策略更新时通过对新旧策略比率的重要性采样和对策略更新比率偏离程度的裁剪机制, 通过限制策略更新的程度, 在保证采样效率的同时, 显著提升了训练过程的稳定性, 这对多智能体环境中的协同学习尤为重要。
3. 仿真结果与分析
此节通过模拟仿真评估和验证所提出的方法。实验场景设定为最大半径2 km的圆形区域, 各通信链路的平均时延为1.9 s; 每个信息包内包含1 024 bit的信息, 时隙长度设定为0.2 s, 信号带宽为10 kHz, 发送节点的最大功率不超过20 W。除非另行说明, 默认情况下: 通信链路数量为3; 数据到达率(单位为信号包每时期)为2, 即每个时期开始时有2个待传输的信号包到达各发送节点; 每个时期包含5个时隙。根据实验数据[16], 式(6)中转移矩阵
$ {\boldsymbol{A}}_d^\ell $ 的元素值满足0.85至0.95之间的均匀分布, 其衡量了信道演化的相关性, 而噪声的能量服从0.04至0.06的均匀分布。文中性能评估的主要指标包括平均吞吐量(throughput, TP), 平均能量效率(energy efficiency, EE)和平均数据队列长度(data queue length, DQL)。令
$ {\eta _{{\text{TP}}}} $ 表示平均TP, 其定义为在T个时期内, 系统每个时期内平均可成功传输的信号包数量, 平均TP为$$ {\eta _{{\text{TP}}}} = \frac{1}{{TN}}\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^N {{S_i}} } (t) $$ (26) 其单位为信号包每时期(packet/epoch), 表示每时期内可成功传输信号包数量。
$$ {\eta _{{\text{EE}}}} = \frac{{\displaystyle \sum\limits_{t = 1}^T {\displaystyle \sum\limits_{i = 1}^N {{S_i}} } (t)}}{{\displaystyle \sum\limits_{t = 1}^T {{E_{{\text{total}}}}(t)} }} $$ (27) 式中,
$ {\eta _{{\text{EE}}}} $ 为能量效率EE, 其定义为在T个时期内, 系统成功传输的信号包总数与总能量消耗的比值。其单位为信号包每焦耳(packet/J), 表示每焦耳可传输信号包数量。
$$ {\eta _{{\text{DQL}}}} = \frac{1}{{TN}}\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^N {{Q_i}} } (t) $$ (28) 式中,
$ {\eta _{{\text{DQL}}}} $ 为平均数据队列长度DQL, 其定义为一个传输时期内, 所有发送节点因未及时传输而存储于数据缓存中的平均信号包数量。该指标与信息的平均传输延迟正相关, 可以衡量数据从发送到接收的传输延迟, 并反映系统在不同负载条件下管理数据流量的能力。其单位为信号包每时期(packet/epoch), 表示每时期内系统留滞在缓存的信号包数量。
文中采用Xuance框架[23]构建了一个仿真的水下通信环境, 以验证提出方法的有效性。具体的MARL算法相关参数设置如下: Actor和Critic网络均包含3个隐藏层, 每层包含64个神经元, 适中的神经元数量可平衡网络的估计性能与过拟合风险; 策略网络和价值网络的学习率均设置为0.001, 以确保合适的学习速率; 经验缓冲池大小为500, 包含可学习的轨迹数量; 评论家网络使用ReLU激活函数, Actor网络的输出层使用Sigmoid函数; 折扣因子设置为0.99, 以避免过度关注未来收益导致的学习发散; 奖励权重分别为0.8和0.2, 以重点保障数据传输成功的同时节省传输能耗; 训练过程共进行4个周期, 每个周期包含50 000个时期, 以确保两个网络的充分训练。
为了评估提出算法的性能, 文中基于文献[15]改进了其提出的MAC协议, 形成了MARL-MAC, 其本质上是结合MARL的扩展, 作为文中提出的跨层优化方法的对比参考。
3.1 TP分析
图5 展示了不同数据到达率下两种方法的TP对比结果。在低流量条件(数据到达率为0～1.2)下, MARL-TS 协议的TP与 MARL-MAC 协议相近, 表明在系统未过载时, 两种方法在信息传输能力上差异不大。然而, 随着数据到达率的增加, 系统逐渐难以维持流入与流出的数据平衡, 最终进入流量过载状态。在此情况下, MARL-TS 协议的优势逐步显现。MARL-TS与MARL-MAC的TP分别在数据到达率2与1左右时开始趋于平缓, 表明此时两种方法由承载平衡转变至系统过载。由此可见, MARL-MAC 协议更早达到数据承载能力的上限, 表明 MARL-TS拥有更高的传输负载适应性, 能够更高效地利用网络资源, 提高传输效率。
值得注意的是, 在低流量条件下, 即当两种方法均能承载所有节点产生的流量时, 它们的吞吐量几乎相等。而在高流入场景下, 当系统无法完全承载流量时, 两种方法的TP与DQL呈线性负相关关系, 因此后续不再重复分析TP变化。
3.2 不同数据到达率下的性能比较
图6展示了不同数据流入量下, 两种方法的EE性能。可以看出, 两种方法的 EE 均在数据到达率1~2时增速放缓, 这是由于系统逐渐进入过载状态, 冲突增多, 整体效率下降。整体来看, MARL-TS 协议在所有数据到达率下均优于 MARL-MAC 协议, EE平均提升0.029。在较低的数据到达率下, 两种协议之间的差异较小, 因为系统尚未完全过载, 传输资源相对充足。然而, 即使在低数据到达率下, MARL-TS协议仍表现略优, 这得益于其对时变信道的预测和利用, 在信道不适合传输的时候少传输, 反之则多传输, 从而提高了EE。随着数据到达率的增加, MARL-TS协议的优势逐渐显现。在中高数据到达率下, MARL-TS能够通过冲突避免机制, 适应不断变化的流量条件并优化能量消耗, 从而保持较高的能量效率。相比之下, MARL-MAC协议在动态流量管理方面的表现较差, 其性能在这些条件下有所下降。
图 6 不同数据到达率下能量效率的比较Figure 6. Comparison of energy efficiency at different data arrival rates图7展示了不同数据到达率下, 两种方法的DQL性能。MARL-TS与MARL-MAC的DQL分别在数据到达率1 与2左右由缓慢增长变为由系统逐渐过载导致的快速爬升。可以发现, 随着数据到达率的增加, MARL-TS和MARL-MAC的队列长度均呈现上升趋势, 表明流量增加不可避免地导致传输失败与重传。在数据到达率达到1.2的时候, MARL-MAC的数据流量已经开始过载, 数据缓存量急剧上升, 但MARL-TS的这一过载阈值却在数据到达率2.2以上。MARL-TS通过跨层优化和数据包的合理重叠, 不仅更有效地控制了队列长度, 还延迟了过载的发生, 表明其在处理高流量负载方面具有更强的能力, 从而提供了更高的传输潜力。
图 7 不同数据到达率下平均数据队列长度的比较Figure 7. Comparison of average data queue length at different data arrival rates3.3 不同链路数量下的性能比较
图8展示了不同通信链路数量下两种方法的EE性能。随着节点数量的增加, MARL-TS 的 EE 始终保持较高水平, 而 MARL-MAC 在链路数增加至 5 后 EE 略有提升, 这是由于节点数量增加提高了所有链路发送成功次数总和。整体来看, MARL-TS的EE平均高0.034, 这表明MARL-TS在多节点环境中展现出更强的鲁棒性和可扩展性。其分布式信道分配机制和负载均衡策略能够有效管理信道竞争并减少能量浪费, 避免因节点冲突导致的重复传输能耗。
图 8 不同链路数量下能量效率的比较Figure 8. Comparison of energy efficiency with different number of links图9展示了不同通信链路数量下, 两种方法的DQL性能。可以看出, 随着链路数量增长至 5之后, 两种方法的 DQL 均呈现加速增长趋势, 表明各发送节点的发送机会随着链路数量增加而减少。然而, MARL-TS协议始终比MARL-MAC协议实现更低的数据缓存量, 每时期平均少0.58 个信号包。随着节点数量的增加, MARL-MAC协议在密集网络中协调传输的能力受到限制, 导致信息传输延迟迅速增加。相比之下, MARL-TS表现出卓越的可扩展性。即使在节点数量较多的情况下, 其动态资源分配能有效减少网络拥塞, 保持高效的数据缓存管理, 确保较低的信息传输延迟。
图 9 不同链路数量下平均队数据列长度的比较Figure 9. Comparison of the average data queue length for different number of links3.4 不同时隙数量下的性能比较
图10展示了每个时期内不同时隙数量下, 两种方法的EE性能。图示结果表明, MARL-TS协议在所有时隙数量下均优于MARL-MAC协议, EE平均提升了0.03。随着时隙数量的增加, 两种方法的EE均有所下降, 主要原因是强化学习方法的动作空间和状态空间增大, 增加了决策复杂度。然而, MARL-TS依然展现出更强的适应性, 能够有效利用额外的时隙优化传输调度, 从而缓解动作空间扩展带来的计算复杂度。此外, 在时隙数量为6-10时, MARL-TS的EE曲线出现轻微震荡, 这是由于较大的动作空间可能导致训练过程中性能收敛的波动。尽管如此, MARL-TS仍然能够在不同时隙数量下维持较高的EE, 进一步验证了其在动态资源分配中的优势。
图 10 不同时隙数量下能量效率的比较Figure 10. Comparison of energy efficiency at different number of time slots图11展示了每个时期内不同时隙数量下, 两种方法的DQL性能。随着时隙数量的增加, 特别是在时隙数超过7之后, 两种协议的DQL均呈现下降趋势。这是由于更多的时隙提供了更多的传输机会, 有效减少了信息传输延迟。然而, MARL-TS始终实现了比MARL-MAC更低的数据缓存量, 每时期平均少0.81个信号包。其优异性能归因于其能够有效地将流量分配到可用时隙中, 从而确保更好的流量管理, 减少了拥塞并提高了传输效率。
图 11 不同时隙数量下平均数据队列长度的比较Figure 11. Comparison of average data queue length for different number of time slots3.5 单智能体强化学习
此外, 文中还评估了 MARL-TS 的单智能体强化学习(single-agent reinforcement learning based-transmission scheduling, SARL-TS)版本, 即由单个策略网络同时为所有发送节点生成传输策略, 以进一步分析 MARL-TS 在多智能体学习环境下的性能优势。文中考虑以下3个系统未过载且学习相对容易的场景:
1)场景1: 数据到达率为0.3, 节点数为3, 时隙数为 5; 2)场景2: 数据到达率为0.1, 节点数为3, 时隙数为5; 3)场景3: 数据到达率为2, 节点数为3, 时隙数为10。
在3种场景下对两种方法的EE和DQL性能进行了仿真测试, 结果如表1所示。可以看出, 即使在状态与动作空间较为适中的情况下, SARL-TS的收敛难度与性能均不如多MARL-TS, 无法生成合理的传输参数决策, 因此通过多智能体学习最优传输参数的有效性得到了验证。
表 1 典型场景中MARL-TS与SARL-TS的性能比较Table 1. Comparison of the performance of MARL-TS and SARL-TS in typical scenarios指标 方法 场景1 场景2 场景3 EE MARL-TS 0.0 789 0.0 693 0.0 789 SARL-TS 0.0 697 0.0 380 0.0 457 DQL MARL-TS 0.1 190 0.0 428 0.1 990 SARL-TS 0.3 700 0.2 260 0.5 340 3.6 接收模式分析
为了进一步分析文中提出的MARL-TS协议的决策模式, 评估了提出方法在3个接收节点、每个时期包含5个时隙和数据到达率为2时的场景下的传输策略。
图12展示了高质量信道条件下某发送节点的传输行为。该节点优先选择高信噪比的时隙进行数据传输, 以利用更优的信道条件实现可靠通信。然而, 第3个时隙被跳过以避免对其他接收节点造成干扰。这表明, 所提出的协议在优化自身传输效率的同时, 能够有效减少接收节点之间的干扰。该案例充分体现了文中方法通过合理利用信道质量, 实现能量效率最大化和干扰最小化, 从而显著提升了系统的整体性能。
图 12 高信噪比信道条件下的传输模式例子Figure 12. Example of transmission patterns under high SNR channel conditions图13展示了弱干扰条件下某发送节点的传输行为。发送节点不仅优先选择高信噪比的时隙, 还在干扰较弱的时隙中进行传输。与图11类似, 第3个时隙因可能导致其他链路的干扰而未被选择用于传输。该例子表明, 所提出的协议能够灵活适应干扰条件的变化, 有效平衡传输可靠性与干扰管理。通过合理选择干扰可控的时隙, 协议在更具挑战性的通信环境下, 依然能够保证高效的通信性能。
图 13 弱干扰条件下的传输模式例子Figure 13. Example of transmission patterns under weak interference conditions4. 结束语
文中提出了一种基于多智能体强化学习的多节点水声网络跨层传输方法, 实现了时隙调度与功率分配的联合优化, 有效应对任意水声传播延迟和时变水声信道下的传输调度挑战。实验结果表明, 该方法在网络TP、能量效率和传输延迟方面均取得了显著提升, 尤其在多节点高负载场景下展现出优越的适应性和鲁棒性。未来的研究将进一步拓展决策范围, 引入调制方式及编码率等更多传输参数的优化。此外, 还将探索在无中心节点决策的情况下, 如何利用分布式学习实现高效的网络传输调度, 从而降低额外的通信开销, 提升系统的自主性与可扩展性。
-
图 3 MARL-TS协议中多智能体与环境交互示意图
Figure 3. Schematic diagram of the interaction between multiple agents and the environment in the MARL-TS protocol
图 6 不同数据到达率下能量效率的比较
Figure 6. Comparison of energy efficiency at different data arrival rates
图 7 不同数据到达率下平均数据队列长度的比较
Figure 7. Comparison of average data queue length at different data arrival rates
图 8 不同链路数量下能量效率的比较
Figure 8. Comparison of energy efficiency with different number of links
图 9 不同链路数量下平均队数据列长度的比较
Figure 9. Comparison of the average data queue length for different number of links
图 10 不同时隙数量下能量效率的比较
Figure 10. Comparison of energy efficiency at different number of time slots
图 11 不同时隙数量下平均数据队列长度的比较
Figure 11. Comparison of average data queue length for different number of time slots
图 12 高信噪比信道条件下的传输模式例子
Figure 12. Example of transmission patterns under high SNR channel conditions
图 13 弱干扰条件下的传输模式例子
Figure 13. Example of transmission patterns under weak interference conditions
表 1 典型场景中MARL-TS与SARL-TS的性能比较
Table 1. Comparison of the performance of MARL-TS and SARL-TS in typical scenarios
指标 方法 场景1 场景2 场景3 EE MARL-TS 0.0 789 0.0 693 0.0 789 SARL-TS 0.0 697 0.0 380 0.0 457 DQL MARL-TS 0.1 190 0.0 428 0.1 990 SARL-TS 0.3 700 0.2 260 0.5 340 
下载: 导出CSV
-
[1] NEIRA J, SEQUEIROS C, HUAMANI R, et al. Review on unmanned underwater robotics, structure designs, materials, sensors, actuators, and navigation control[J]. Journal of Robotics, 2021, 1: 5542920. [2] 江子龙, 王焱, 钟雪峰, 等. 基于NS-3的声电协同网络实现及路由性能分析[J]. 电子与信息学报, 2022, 44(6): 2014-2023. doi: 10.11999/JEIT211274JIANG Z L, WANG Y, ZHONG X F, et al. Implementation of acoustic-electric cooperative networks and routing performance analysis based on NS-3[J]. Journal of Electronics & Information Technology, 2022, 44(6): 2014-2023. doi: 10.11999/JEIT211274 [3] 刘千里, 吴晖. 水下无线传感器网络通信技术研究现状及趋势[J]. 舰船电子工程, 2022, 42(9): 20-24.LIU Q L, WU H. Research status and trends of underwater wireless sensor network communication technology[J]. Ship Electronic Engineering, 2022, 42(9): 20-24. [4] 瞿逢重, 付雁冰, 杨劭坚, 等. 应用于海洋物联网的水声通信技术发展综述[J]. 哈尔滨工程大学学报, 2023, 44(11): 1937-1949. doi: 10.11990/jheu.202306023QU F Z, FU Y B, YANG S J, et al. An overview of the development status of underwater acoustic communication technology applied to ocean internet-of-things[J]. Journal of Harbin Engineering University, 2023, 44(11): 1937-1949. doi: 10.11990/jheu.202306023 [5] CHAUDHARY M, GOYAL N, BENSLIMANE A, et al. Underwater wireless sensor networks: Enabling technologies for node deployment and data collection challenges[J]. IEEE Internet of Things Journal, 2022, 10(4): 3500-3524. [6] ZHAO N, YAO N, GAO Z. An adaptive MAC protocol based on time-domain interference alignment for UWANs[J]. The Computer Journal, 2023, 66(12): 3015-3028. [7] 赵昊. 基于深度学习的水声通信物理层技术研究[D]. 广州: 华南理工大学, 2023. [8] PALLARES O, BOUVET P J, RIO J D. TS-MUWSN: Time synchronization for mobile underwater sensor networks[J]. IEEE Journal of Oceanic Engineering, 2016, 41(4): 763-775. doi: 10.1109/JOE.2016.2581658 [9] HSU C C, KUO M S, CHOU C F, et al. The elimination of spatial-temporal uncertainty in underwater sensor networks[J]. IEEE/ACM Transactions on Networking, 2013, 21(4): 1229-1242. [10] HUANG Q H, LI W, ZHAN W C, et al. Dynamic underwater acoustic channel tracking for correlated rapidly time-varying channels[EB/OL]. (2021-03-01)[2025-03-20]. https://arXiv:2103.00859. [11] DU H, WANG X, SUN W, et al. An adaptive MAC protocol for underwater acoustic networks based on deep reinforcement learning[C]//The 6th International Conference on Communications, Information System and Computer Engineering. Guangzhou, China: IEEE, 2025. [12] TOMOVIC S, RADUSINOVI I. DR-ALOHA-Q: A Q-Learning-based adaptive mac protocol for underwater acoustic sensor networks[J]. Sensors, 2023, 23(9): 4474. [13] HUANG Y, WANG H, CHEN Y, et al. Distributed deep reinforcement learning with prioritized replay for power allocation in underwater acoustic communication networks[J]. IEEE Internet of Things Journal, 2024, 11(6): 9915-9928. [14] YE X, YU Y, FU L. Deep reinforcement learning based MAC protocol for underwater acoustic networks[J]. IEEE Transactions on Mobile Computing, 2020, 21(5): 1625-1638. [15] HUANG J J, YE X W, FU L Q. MAC protocol for underwater acoustic multi-cluster networks based on multi-agent reinforcement learning[C]//The 17th International Conference on Underwater Networks & Systems. Guangzhou, China: ACM, 2023, 10: 1-5. [16] WANG C, WANG Z, SUN W, et al. Reinforcement learning-based adaptive transmission in time-varying underwater acoustic channels[J]. IEEE Access, 2017, 6: 2541-2558. [17] WANG H, LI Y, QIAN J. Self-adaptive resource allocation in underwater acoustic interference channel: a reinforcement learning approach[J]. IEEE Internet of Things Journal, 2020, 7(4): 2816-2827. [18] STOJANOVIC M, PREISIG J. Underwater acoustic communication channels: Propagation models and statistical characterization[J]. IEEE Communications Magazine, 2009, 47(1): 84-89. [19] WANG C F, ZHAO W K, BI Z C, et al. A joint power allocation and scheduling algorithm based on quasi-interference alignment in underwater acoustic networks[C]//OCEANS 2022, Virginia, USA: IEEE, 2022. [20] TSATSANIS M K, GIANNAKIS G B, ZHOU G. Estimation and equalization of fading channels with random coefficients[J]. Signal Processing, 1996, 53(2-3): 211-229. [21] SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[EB/OL]. (2007-8-28)[2025-3-11]. https://arxiv.org/abs/1707.06347. [22] YU C, VELU A, VINITSKY E, et al. The surprising effectiveness of PPO in cooperative multi-agent games[J]. Advances in Neural Information Processing Systems. 2022, 35: 24611-24624. [23] Liu W, Cai W, Jiang K. , et al. XUANCE: A comprehensive and unified deep reinforcement learning library[EB/OL]. (2023-12-25)[2025-3-11]. https://arxiv.or-g.abs/2312.16248. -
下载:
点击查看大图
计量
- 文章访问数: 10
- HTML全文浏览量: 6
- PDF下载量: 5
- 被引次数: 0
