Prediction of SNR Based on SVR and Adaptive Transmission Power Method for Underwater Acoustic Communication
-
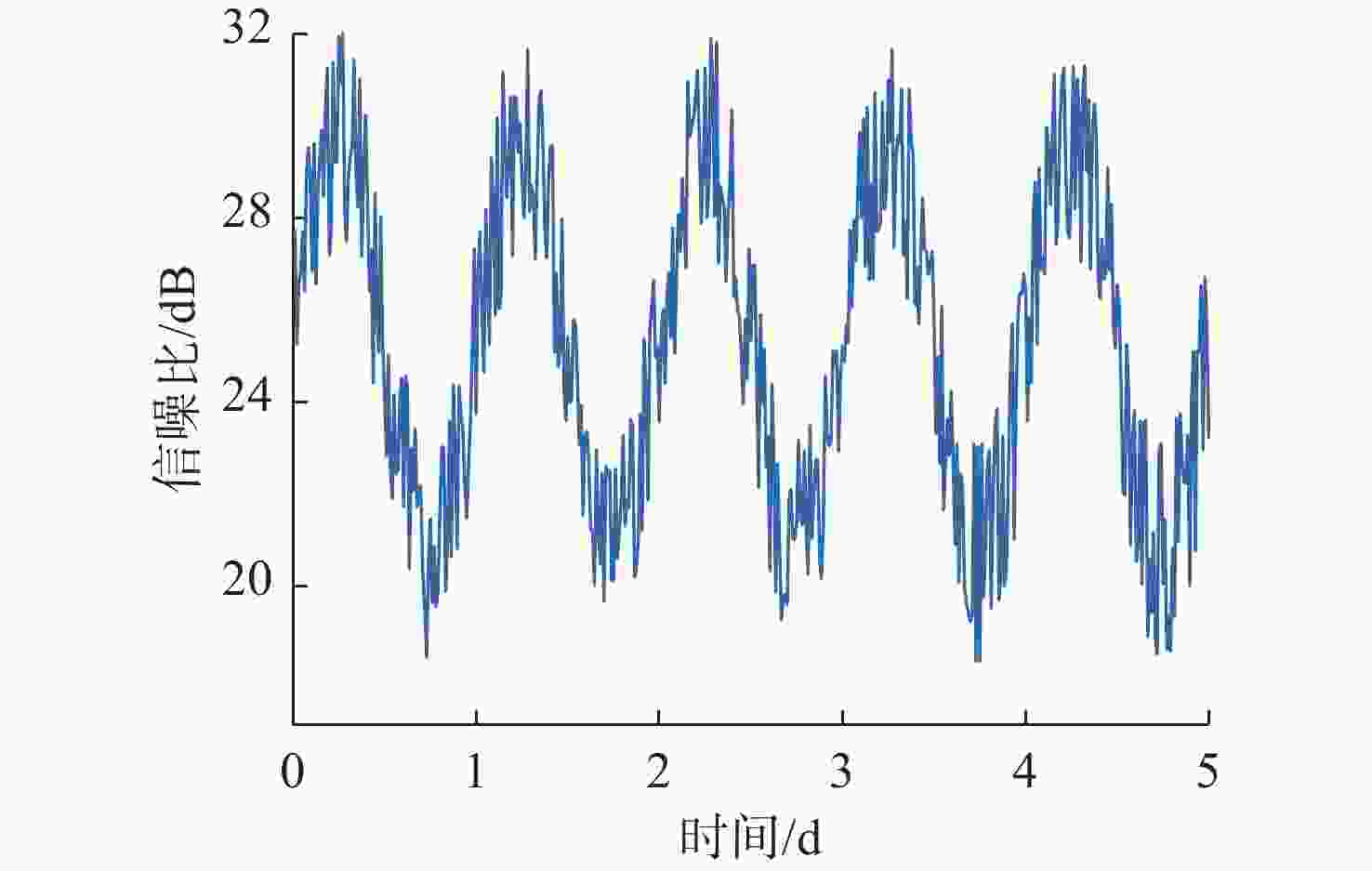
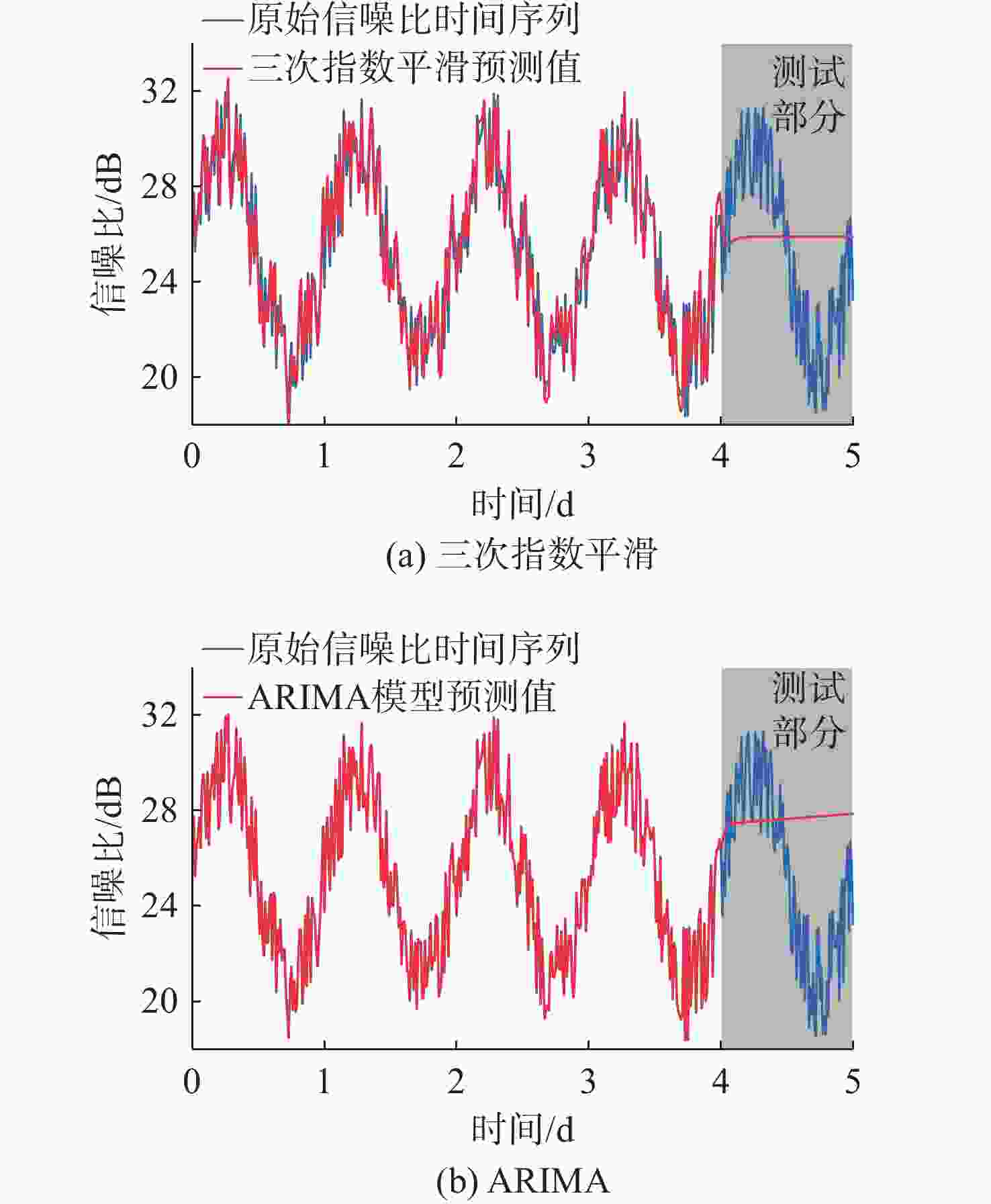
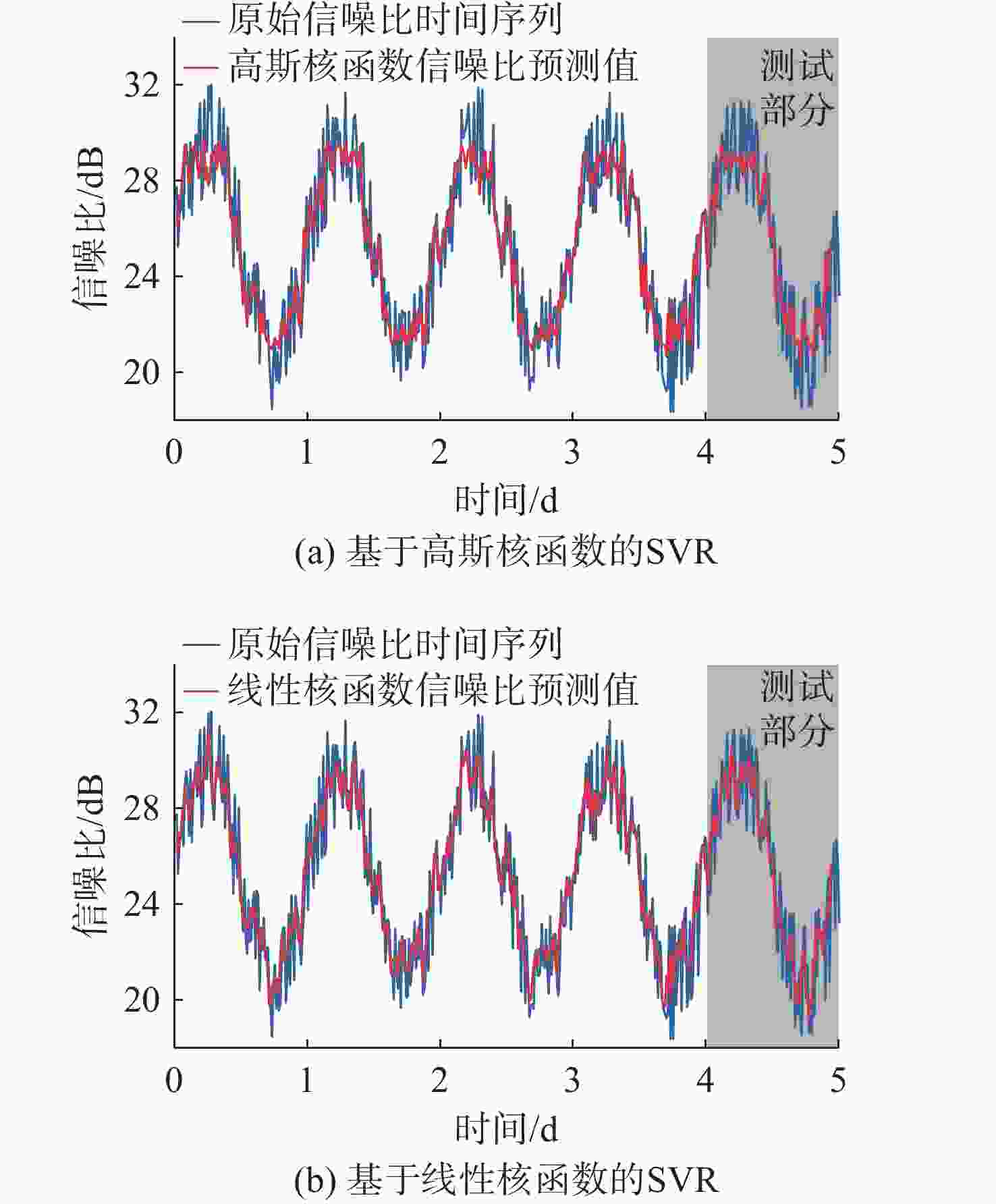
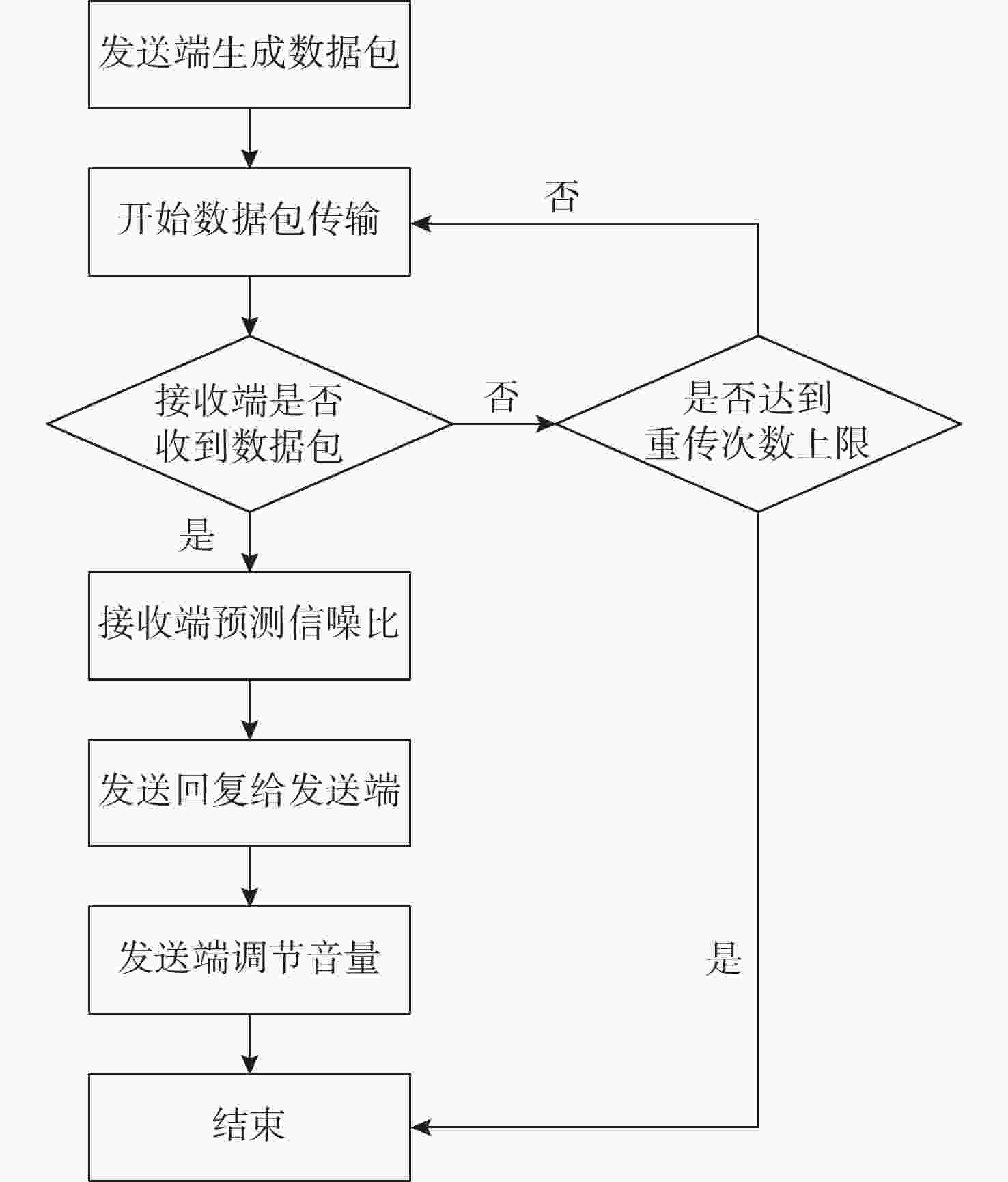
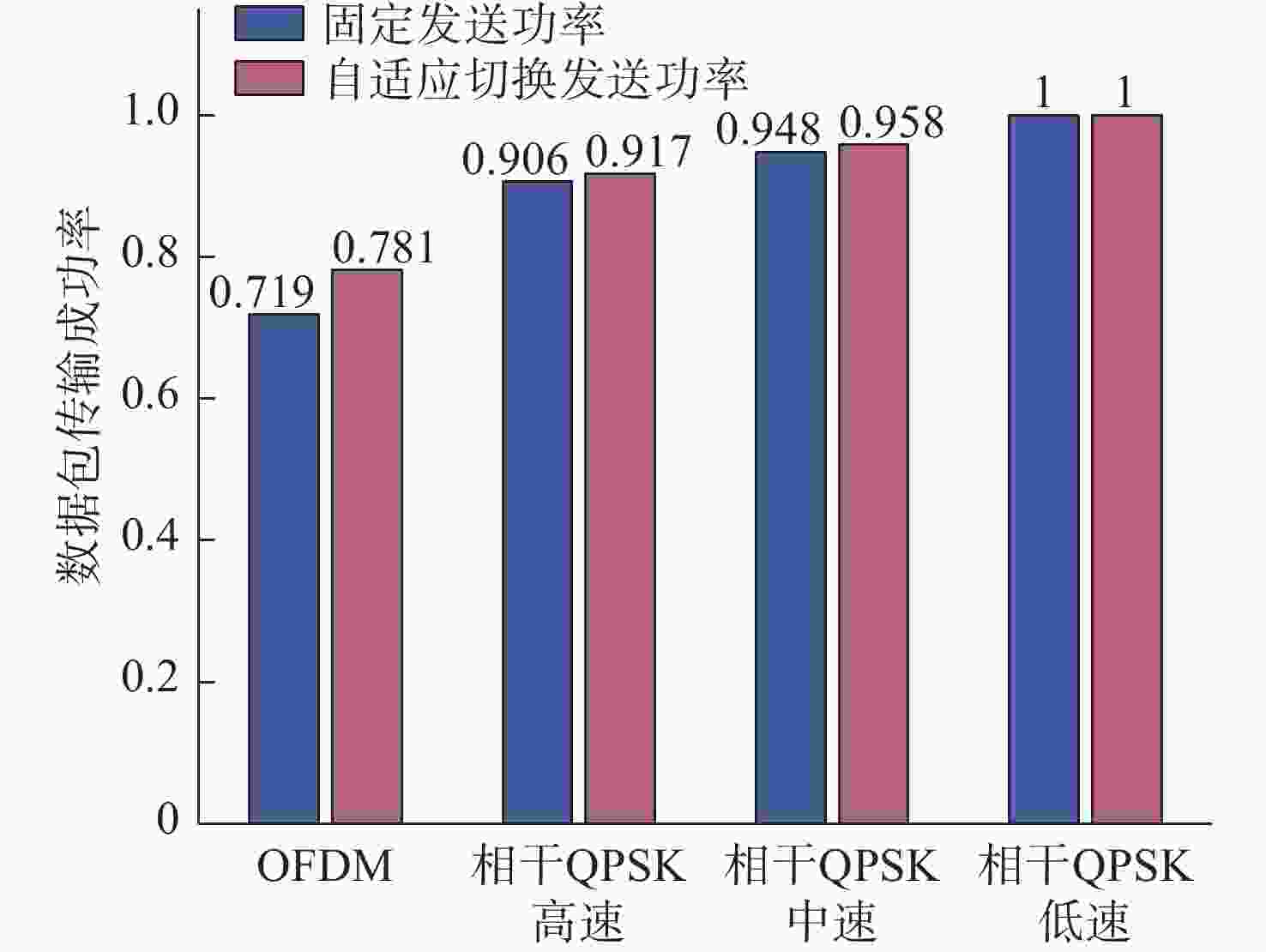
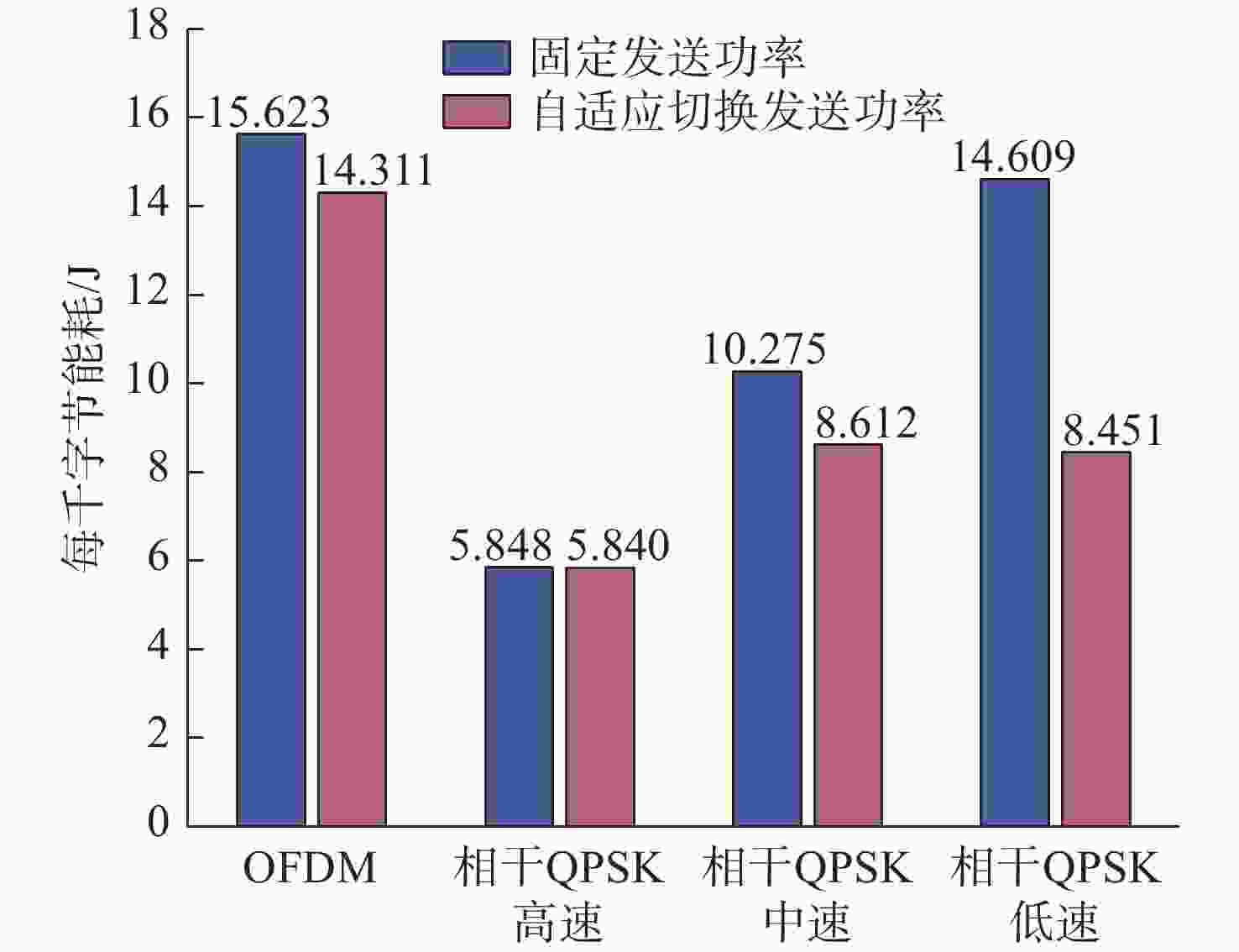
摘要: 海洋环境噪声受海浪、风雨、海洋生物、船舶及工业等诸多因素影响, 其功率具有较强的随机性; 同时, 海面温度及潮汐高度等因素的持续作用也会使其功率具有一定的周期性特征。水下环境噪声在水声通信时会直接影响通信误包率, 提高发送功率可增大接收信噪比、降低误包率, 但也会提高通信平均能耗。因此, 为了降低水声通信的误包率与平均能耗, 文中提出基于支持向量回归(SVR)算法对信噪比时间序列进行分析预测, 并提出基于信噪比预测的水声通信发送功率自适应方法。仿真结果表明, 相比于指数平滑及差分整合移动平均自回归模型(ARIMA)方法, 基于线性核函数的SVR算法对信噪比预测效果最佳, 在测试数据上的预测误差最小。在不同调制方式下, 所提发送功率自适应方法均可在提高数据包传输成功率的同时降低每千字节能耗。Abstract: Marine environmental noise is influenced by many factors such as ocean waves, wind, rain, marine organisms, ships, and industrial activities. Its power is highly random. However, the continuous effect of factors such as sea surface temperature and tidal height can also make the power have certain periodic characteristics. Underwater environmental noise can directly affect the communication packet error rate during underwater acoustic communication. Although increasing the transmission power can raise the received signal-to-noise ratios and decrease the packet error rate, it also enhances the average energy consumption of communication. Therefore, in order to reduce the packet error rate and average energy consumption of underwater acoustic communication, this paper analyzed and predicted the signal-to-noise ratios time series based on the support vector regression(SVR) algorithm and proposed an adaptive transmission power method for underwater acoustic communication based on signal-to-noise ratio prediction. The simulation results show that compared with the exponential smoothing and autoregressive integrated moving average model(ARIMA) methods, the SVR algorithm based on the linear kernel function has the best performance in predicting signal-to-noise ratios and the smallest prediction error on test data. Under different modulation methods, the proposed adaptive transmission power method for underwater acoustic communication can improve the success rate of data packet transmission while reducing energy consumption per kilobyte.
-
表 1 信噪比时间序列仿真模型参数列表
Table 1. List of parameters for signal-to-noise ratio time series simulation model
参数名称 参数取值 L 96.00 $ {\sigma _{ch}} $ 4.46 $ {\mu _{ch}} $ 22.70 $ {\sigma ^2} $ 5.00 表 2 信噪比时间序列预测方法性能对比
Table 2. Performance comparison of signal-to-noise ratio time series prediction methods
预测方法 训练集
RMSE训练集
MAE测试集
RMSE测试集
MAE三次指数平滑 0.641 0.532 3.722 3.160 ARIMA — — 4.411 3.686 SVR(高斯核) 1.569 1.282 1.958 1.654 SVR(线性核) 1.679 1.400 1.914 1.650 表 3 水声通信机不同发送音量对应功率
Table 3. Power corresponding to different transmission volume of underwater acoustic communicator
音量档位 功率/W 声源级/dB 1 2.5 172 2 5.0 175 3 10.0 178 4 20.0 181 表 4 不同调制方式对应的数据包发送能耗分析
Table 4. Energy consumption analysis of data packet transmission corresponding to different modulation modes
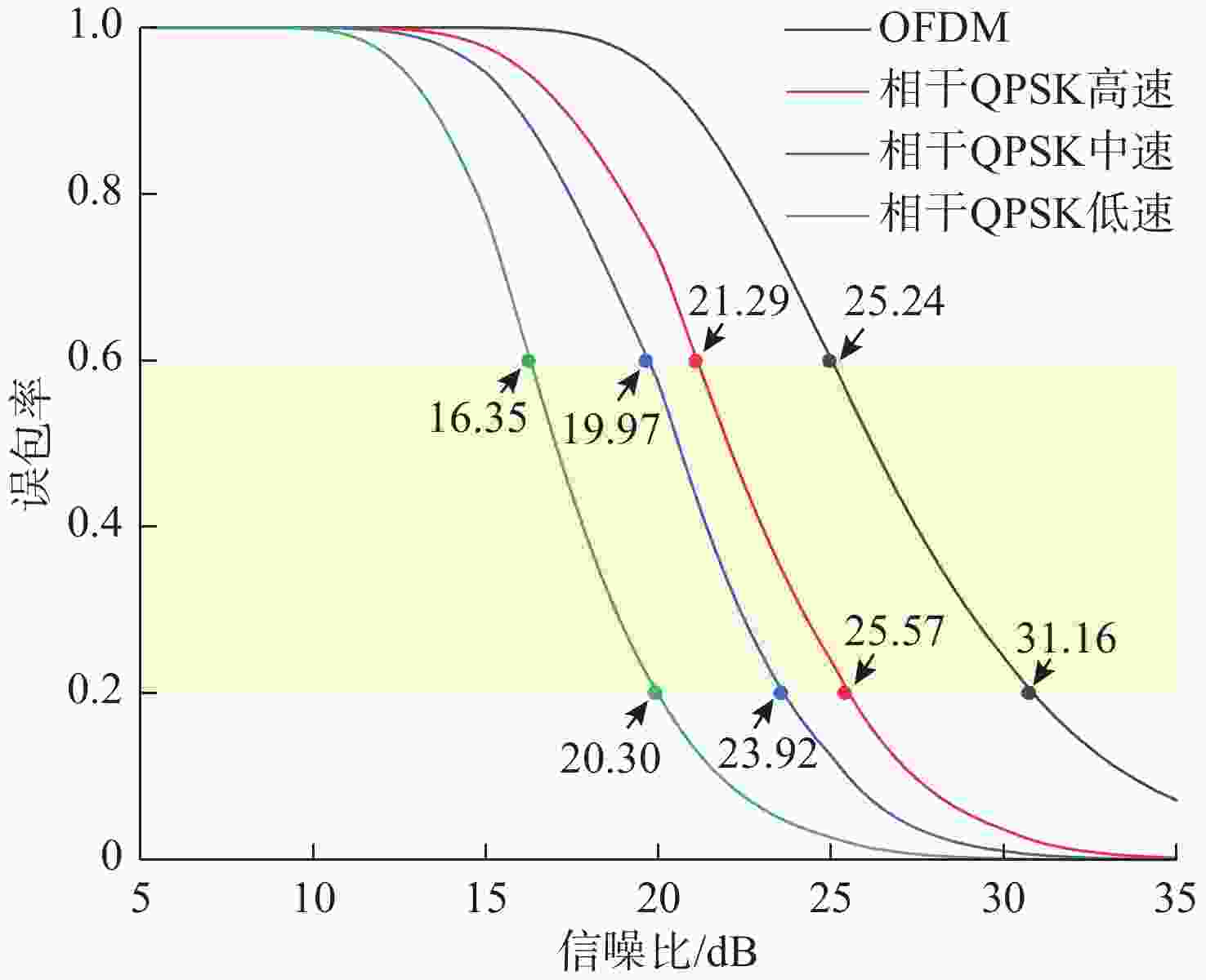
调制方式 数据量/bit 数据包长度/s 数据率/(kbit/s) 音量4档单数据包能耗/mWh 每千字节能耗/mWh 相干QPSK高速 3200 1.1 2.90 6.1 10.67 相干QPSK中速 3200 2.2 1.45 12.2 21.34 相干QPSK低速 3200 4.4 0.73 24.4 42.68 OFDM 1500 0.7 2.14 3.9 14.56 -
[1] 乔钢, 刘凇佐, 刘奇佩. 水声通信网络协议, 仿真与试验综述[J]. 水下无人系统学报, 2017, 25(2): 151-160.QIAO G, LIU S Z, LIU Q P. Review of protocols, simulation and experimentation for underwater acoustic communication network[J]. Journal of Unmanned Undersea Systems, 2017, 25(2): 151-160. [2] LUO H, WANG J, BU F, et al. Recent progress of air/water cross-boundary communications for underwater sensor networks: A review[J]. IEEE Sensors Journal, 2022, 22(9): 8360-8382. doi: 10.1109/JSEN.2022.3162600 [3] 许肖梅. 水声通信与水声网络的发展与应用[J]. 声学技术, 2009, 28(6): 811-816. doi: 10.3969/j.issn1000-3630.2009.06.026XU X M. Development and applications of underwater acoustic communication and networks[J]. Technical Acoustics, 2009, 28(6): 811-816. doi: 10.3969/j.issn1000-3630.2009.06.026 [4] SU W, LIN J, CHEN K, et al. Reinforcement learning-based adaptive modulation and coding for efficient underwater communications[J]. IEEE Access, 2019, 7: 67539-67550. doi: 10.1109/ACCESS.2019.2918506 [5] 吴雨珊. 自适应调制与功率分配的 OFDM 水声通信技术[D]. 哈尔滨: 哈尔滨工程大学, 2019. [6] 孙秋实. 水声通信的自适应调制编码方法研究[D]. 杭州: 浙江大学, 2023. [7] QARABAQI P, STOJANOVIC M. Adaptive power control for underwater acoustic communications[C]//OCEANS 2011 IEEE-Spain. Santander, Spain: IEEE, 2011: 1-7. [8] WANG Z, WANG C, SUN W. Adaptive transmission scheduling in time-varying underwater acoustic channels[C]//OCEANS 2015-MTS/IEEE Washington. Washington, USA: IEEE, 2015: 1-6. [9] 杨逍宇, 马伯乐, 周跃海, 等. 面向长时水声通信数据采集与评估的浮标设计与实现[J]. 数字海洋与水下攻防, 2022, 5(4): 279-284.YANG X Y, MA B L, ZHOU Y H, et al. Design and implementation of buoy for long-time underwater acoustic communication data acquisition and evaluation[J]. Digital Ocean & Underwater Warfare, 2022, 5(4): 279-284. [10] WANG X W, HE Z Q, HU Y, et al. Adaptive modulation and feedback strategy for an underwater acoustic link[C]//2022 Sixth Underwater Communications and Networking Conference(UComms). Seattle, Washington, USA: IEEE, 2022: 1-5. [11] Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20: 273-297. doi: 10.1109/TITS.2004.837813 -





 下载:
下载: