基于伪线性卡尔曼滤波的水下高速动目标短时运动分析

赵俊浩; 马晖; 王明洲; 张俊; 曹浩

doi:10.11993/j.issn.2096-3920.2024-0171

基于伪线性卡尔曼滤波的水下高速动目标短时运动分析

doi: 10.11993/j.issn.2096-3920.2024-0171

中国船舶集团公司第705研究所, 陕西西安, 710077

详细信息

作者简介:
赵俊浩(2001-), 男, 硕士研究生, 主要研究方向为数学建模与仿真

中图分类号: TP242.6; TB56
计量
- 文章访问数: 14
- HTML全文浏览量: 12
- PDF下载量: 1
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-18
- 修回日期: 2025-02-10
- 录用日期: 2025-02-17
- 网络出版日期: 2025-07-08

Underwater High-speed Target short-time Target Motion Analysis Based on Pseudolinear Kalman filter

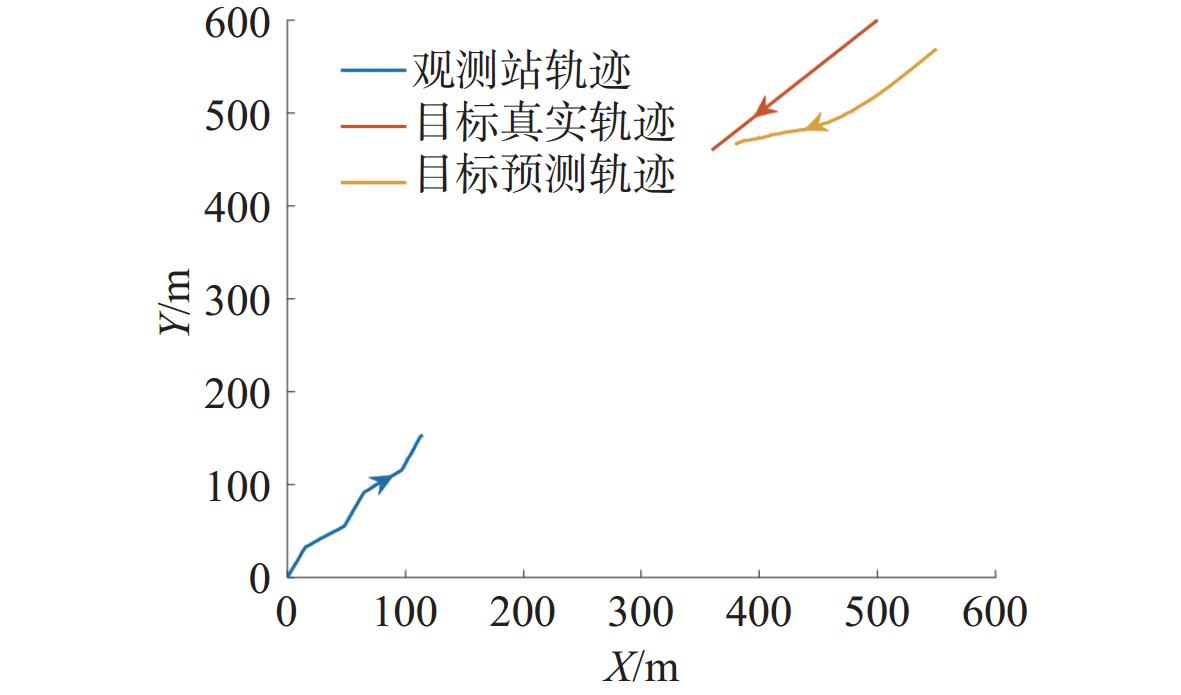
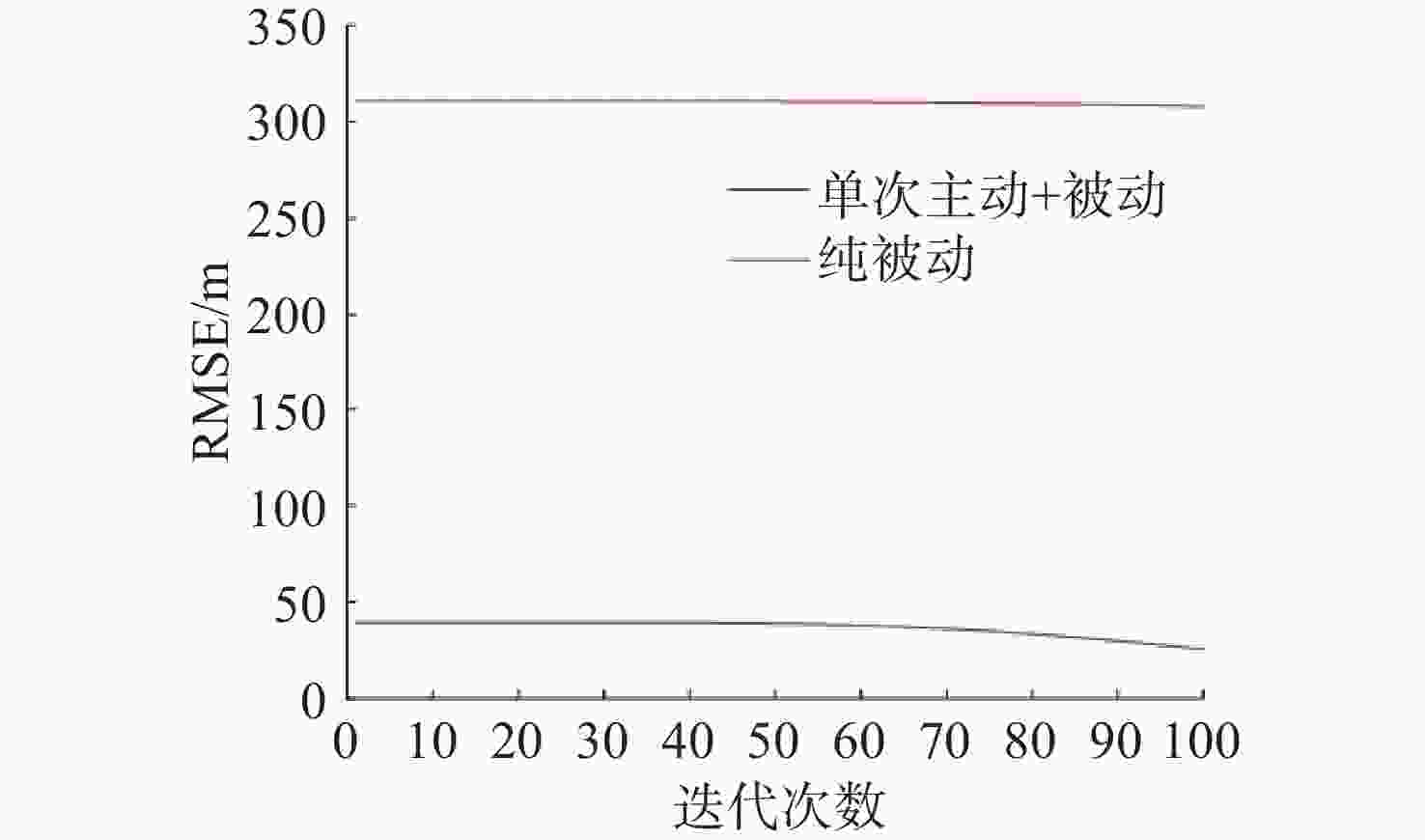
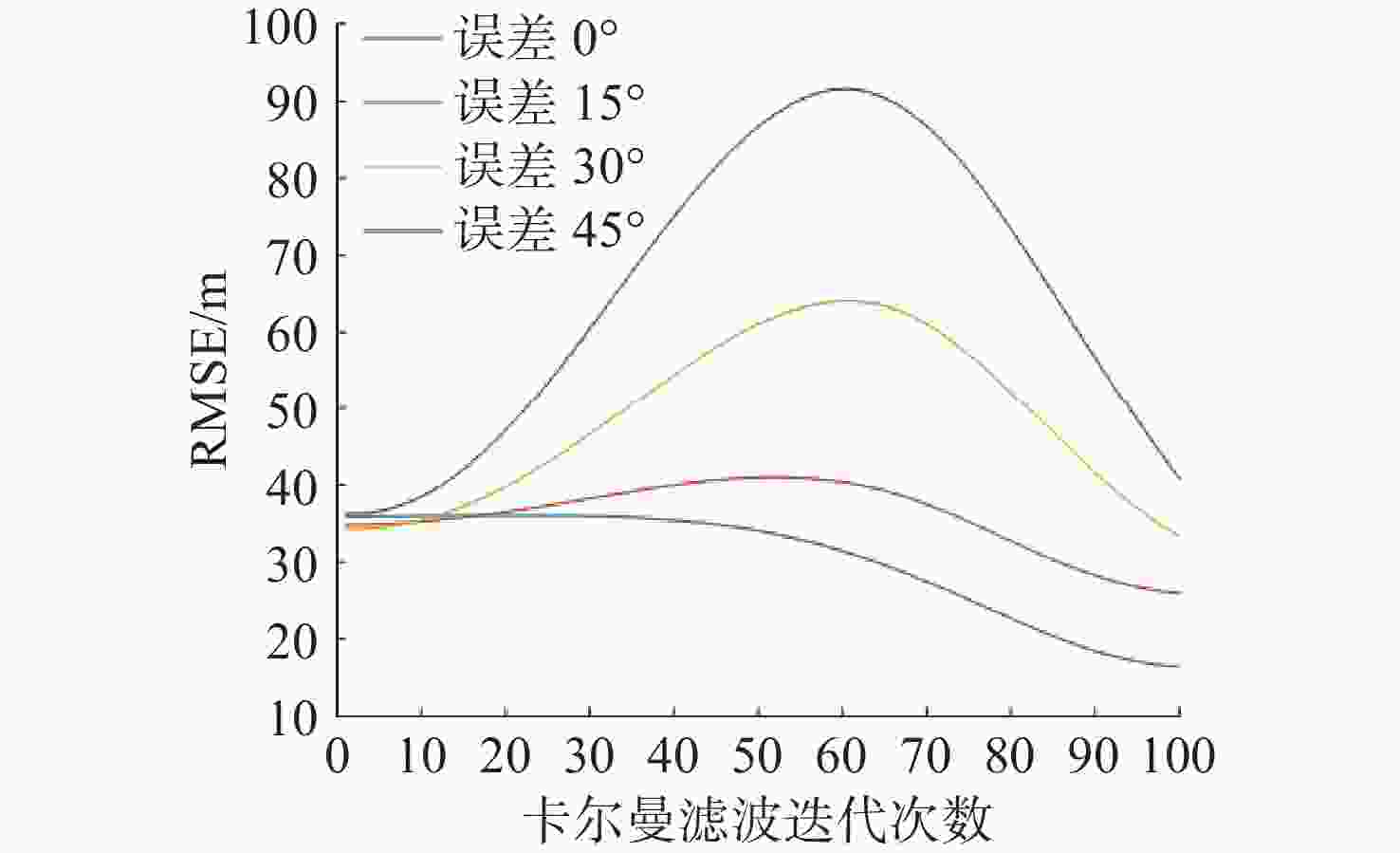
The 705 Research Institute, China Shipbuilding Industry Corporation Limited, Xi’an 710077

摘要

摘要: 针对水下高速动目标探测过程中主动探测周期长、数据不连续, 被动探测无法获得目标距离及难以快速进行目标运动要素有效解算的问题, 提出了基于伪线性卡尔曼滤波的水下高速动目标短时运动分析方法。该方法仅在探测初始时使用一次主动探测, 是一种水平面内的以被动为主、主动为辅的被动目标运动分析(TMA)方法。文中建立了数学模型并给出迭代方程, 基于目标在大部分观测时间内均保持匀速运动的先验假设, 在目标匀速运动条件下进行仿真分析, 使用Monte-Carlo方法计算了预测轨迹的均方根误差。仿真实验结果表明, 该方法相较于纯被动探测下的纯方位TMA方法误差更小, 且能够在短时间内实现对目标运动要素解算收敛, 收敛时间不大于10 s。
- 目标运动分析 /
- 纯方位 /
- 动目标
Abstract: This paper addresses the problems encountered in detecting underwater high-speed moving targets, namely the long active detection cycle leading to discontinuous data, and the inability of passive detection to obtain target range, thus making it difficult to quickly and effectively calculate target motion parameters. To overcome these issues, a short-term motion analysis method for underwater high-speed moving targets based on pseudo-linear Kalman filtering is proposed. This method employs only one initial active detection at the beginning and is primarily a passive-acoustic based target motion analysis(TMA) method within the horizontal plane, supplemented minimally by active detection. Mathematical models are established, and iterative equations are provided. Based on the prior assumption that the target maintains constant-velocity motion for the majority of the observation time, simulation analysis is conducted under constant-velocity motion conditions. The root mean square error (RMSE) of the predicted trajectory is calculated using the Monte Carlo method. Simulation results demonstrate that, compared to bearing-only TMA using purely passive detection, this method achieves significantly smaller errors and enables rapid convergence of the target motion parameter solution within a short timeframe, with convergence achieved within no more than 10 seconds.
- target motion analysis /
- bearings-only /
- moving target

HTML全文

图 1 单次仿真轨迹图

Figure 1. Single simulation trajectory

下载: 全尺寸图片幻灯片

图 2 预测轨迹平均误差曲线对比图

Figure 2. Comparison chart of predicted trajectory average error curves

下载: 全尺寸图片幻灯片

图 3 初始航向预测误差对收敛性的影响

Figure 3. The effect of the initial heading prediction error on convergence

下载: 全尺寸图片幻灯片

表 1 算法框架

Table 1. Algorithmic framework

算法1: 基于PLKF的水下高速动目标短时运动分析方法

输入: 观测站航行轨迹${{\boldsymbol{X}}_{\text{a}}}$, 船舶航行轨迹${{\boldsymbol{S}}_{k}} = \left( {{x_{\text{s}}}\left( k \right), {y_{\text{s}}}\left( k \right)} \right)$, 主动探测得到的目标初始位置坐标$\left( {{{\hat x}_{\text{t}}}\left( 0 \right), {{\hat y}_{\text{t}}}\left( 0 \right)} \right)$, 目标航速大小经验值范围$\left( {{v_{{\text{t}}, {\text{min}}}}, {v_{{\text{t}}, {\text{max}}}}} \right)$仿真周期总个数$N$, 观测站被动探测目标的观测矢量${{\boldsymbol{Z}}_k} = {{{\tilde {\boldsymbol{\theta}} }}_k}$。输入初始误差协方差矩阵${\boldsymbol{P}}_0^{{\text{pre}}}$, 策动噪声协方差矩阵${{\boldsymbol{Q}}_k}$, 量测噪声协方差矩阵${{\boldsymbol{V}}_k}$。输入状态转移矩阵${\boldsymbol{A}}$。
输出: 目标的预测轨迹${\hat {\boldsymbol{X}}_{{\text{t}}, k}}$其中$k = 1, 2, \cdots, N$
1. 估计目标的初始航向
　　　${\psi _{{\text{t}}, 0}} = {\text{arctan}}\left( {\dfrac{{{y_{\text{s}}}\left( 0 \right) - {{\hat y}_{\text{t}}}\left( 0 \right)}}{{{x_{\text{s}}}\left( 0 \right) - {{\hat x}_{\text{t}}}\left( 0 \right)}}} \right)$
2. 估计目标航速$ {v}_{\text{t}} \in \left({v}_{\text{t, min}}, {v}_{\text{t, max}}\right) $
3. 估计目标初始状态向量
　　　${\boldsymbol{X}}_0^{{\text{pre}}} = {\left[ {{{\hat x}_{\text{t}}}\left( 0 \right), {{\hat y}_{\text{t}}}\left( 0 \right), {v_{\text{t}}}{\text{sin}}\left( {{\psi _{{\text{t}}, 0}}} \right), {v_{\text{t}}}{\text{cos}}\left( {{\psi _{{\text{t}}, 0}}} \right)} \right]^{\text{T}}}$
4. 计算新的观测矢量$ {{\boldsymbol{Z}}}_{k}\leftarrow {{\boldsymbol{u}}}_{k}^{\text{T}}{{\boldsymbol{S}}}_{k}, k=1, 2, \cdots , N $
5. for k = 2 to N do
6. 计算最佳增益矩阵
　　　${{\boldsymbol{K}}_k} \leftarrow {\boldsymbol{P}}_k^{{\text{pre}}}{{\boldsymbol{u}}_k}{{\boldsymbol{M}}^{\text{T}}}\left( {{\boldsymbol{u}}_k^{\text{T}}{\boldsymbol{MP}}_k^{{\text{pre}}}{{\boldsymbol{u}}_k}{{\boldsymbol{M}}^{\text{T}}} + {V_k}} \right)$
7. 估计目标状态矢量
　　　${\hat {\boldsymbol{X}}_{\text{t}}}k \leftarrow {\boldsymbol{X}}_k^{{\text{pre}}} + {{\boldsymbol{K}}_k}\left( {{\boldsymbol{Z}}_k^{'} - {\boldsymbol{u}}_k^{\text{T}}{\boldsymbol{M}}{\boldsymbol{X}}_k^{{\text{pre}}}} \right)$
8. 估计误差协方差矩阵
　　　${{\boldsymbol{P}}_k} \leftarrow \left( {{\boldsymbol{I}} - {{\boldsymbol{K}}_k}{{\boldsymbol{u}}_k}{{\boldsymbol{M}}^{\text{T}}}} \right){\boldsymbol{P}}_k^{{\text{pre}}}$
9. 计算下一轮迭代的目标状态矢量先验估计
　　　${\boldsymbol{X}}_{k + 1}^{{\text{pre}}} \leftarrow A{\hat {\boldsymbol{X}}_k}$
10. 计算下一轮迭代的误差协方差矩阵先验估计
　　　${\boldsymbol{P}}_{k + 1}^{{\text{pre}}} \leftarrow {\boldsymbol{AP}}_k^{{\text{pre}}}{{\boldsymbol{A}}^{\text{T}}} + {{\boldsymbol{Q}}_k}$
11. return ${\hat {\boldsymbol{X}}_{\text{t}}}$

下载: 导出CSV

表 2 仿真参数表

Table 2. Table of simulation parameters

参数	大小
目标航速	25 m/s
观测站航速	25 m/s
目标初始位置	(500 m, 600 m)
观测站初始位置	(0 m, 0 m)
目标初始航向	正西南(135°)
观测站初始航向中心	正东北(−45°)
观测站机动扇面角	$ \pm {15^ \circ }$
观测站被动探测采样周期	0.1 s
单次仿真时间	10 s
距离观测误差	2.5 %
角度观测误差	${3^ \circ }$
速度大小估计误差	$ \pm 10{\text{% }}$

下载: 导出CSV

参考文献(12)

[1]	丁乐乐, 顾天军, 赵宇潇. 美无人潜航器军事应用与发展策略思考[J/OL]. 指挥控制与仿真. https://link.cnki.net/urlid/32.1759.TJ.20250610.2134.002. DING L L, GU T J, ZHAO Y X, Thoughts on the military applications and development strategies of US UUV[J]. Command Control & Simulation, 2025, 47.
[2]	孙大军, 张艺翱, 滕婷婷, 等. 单站水下方位频率机动TMA方法[J]. 声学学报, 2024, 49(4): 683-695. doi: 10.12395/0371-0025.2023077 SUN Dajun, ZHANG Yiao, TENG Tingting, HU Zhejian. A single-platform underwater maneuvering target motion analysis method based on bearing and frequency measurements[J]. ACTA ACUSTICA, 2024, 49(4): 683-695. doi: 10.12395/0371-0025.2023077
[3]	朱宣城. 基于粒子滤波的单站纯方位TMA[D]. 哈尔滨: 哈尔滨工程大学, 2023.
[4]	郑艺, 王明洲. 一种滑动后向递推的EKF纯方位目标跟踪方法[J]. 水下无人系统学报, 2020, 28(6): 663-669. ZHENG Yi, WANG Ming-zhou. Sliding Backward Recursive EKF Bearings-Only Target Tracking Method[J]. Journal of Unmanned Undersea Systems, 2020, 28(6): 663-669.
[5]	郑艺, 王明洲. 基于初值更新的水下纯方位短时目标跟踪[J]. 水下无人系统学报, 2021, 29(2): 189-195. ZHENG Yi, WANG Ming-zhou. Underwater Bearings-Only Short Time Target Tracking Based on Initial Value Updating[J]. Journal of Unmanned Undersea Systems, 2021, 29(2): 189-195.
[6]	ZHANG J Y, XU Z G. Bearings-only target motion analysis via instrumental variable estimation[J]. IEEE Transactions on Signal Processing: A publication of the IEEE Signal Processing Society, 2010, 58(11): 5523-5533.
[7]	欧阳林强. 基于纯方位目标跟踪的伪线性卡尔曼滤波算法研究[D]. 成都: 电子科技大学, 2023.
[8]	董彦璐. 水声单站纯方位TMA技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2022.
[9]	MILLER A B, MILLER B M. Underwater target tracking using bearing-only measurements[J]. Journal of Communications Technology and Electronics, 2018, 63(6): 643-649. doi: 10.1134/S1064226918060207
[10]	郑艺, 王明洲, 胡友峰. 改进的中心差分卡尔曼滤波水下被动目标跟踪[J]. 舰船科学技术, 2021, 43(1): 154-160. ZHENG Yi, WANG Ming-zhou. Improved central differential Kalman filter for underwater passive target tracking[J]. Ship Science And Technology, 2021, 43(1): 154-160.
[11]	Badriasl L, Arulampalam S, Nguyen N, et al. An Algebraic Closed-form Solution for Bearings-only Maneuvering Target Motion Analysis from a Nonmaneuvering Platform[J]. IEEE Transactions on Signal Processing, 2020(99): 1-16.
[12]	Wang Y, Zhang X, Wang J, et al. Underwater maneuvering target motion analysis using delayed azimuth angles[J]. Ocean Engineering, 2024, 311(P2): 118901.