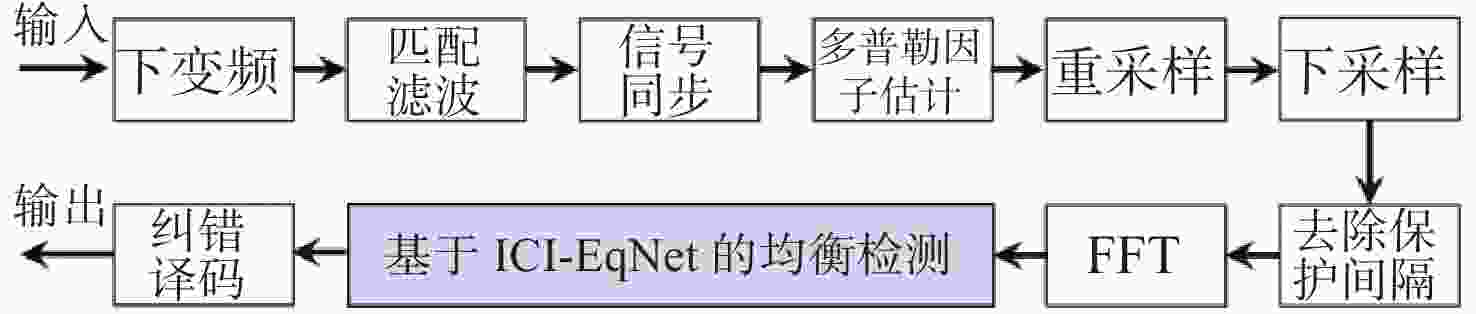
Underwater Acoustic Rapidly Time-Varying Channel Equalization Technique Integrating Deep Learning and Domain Knowledge
-
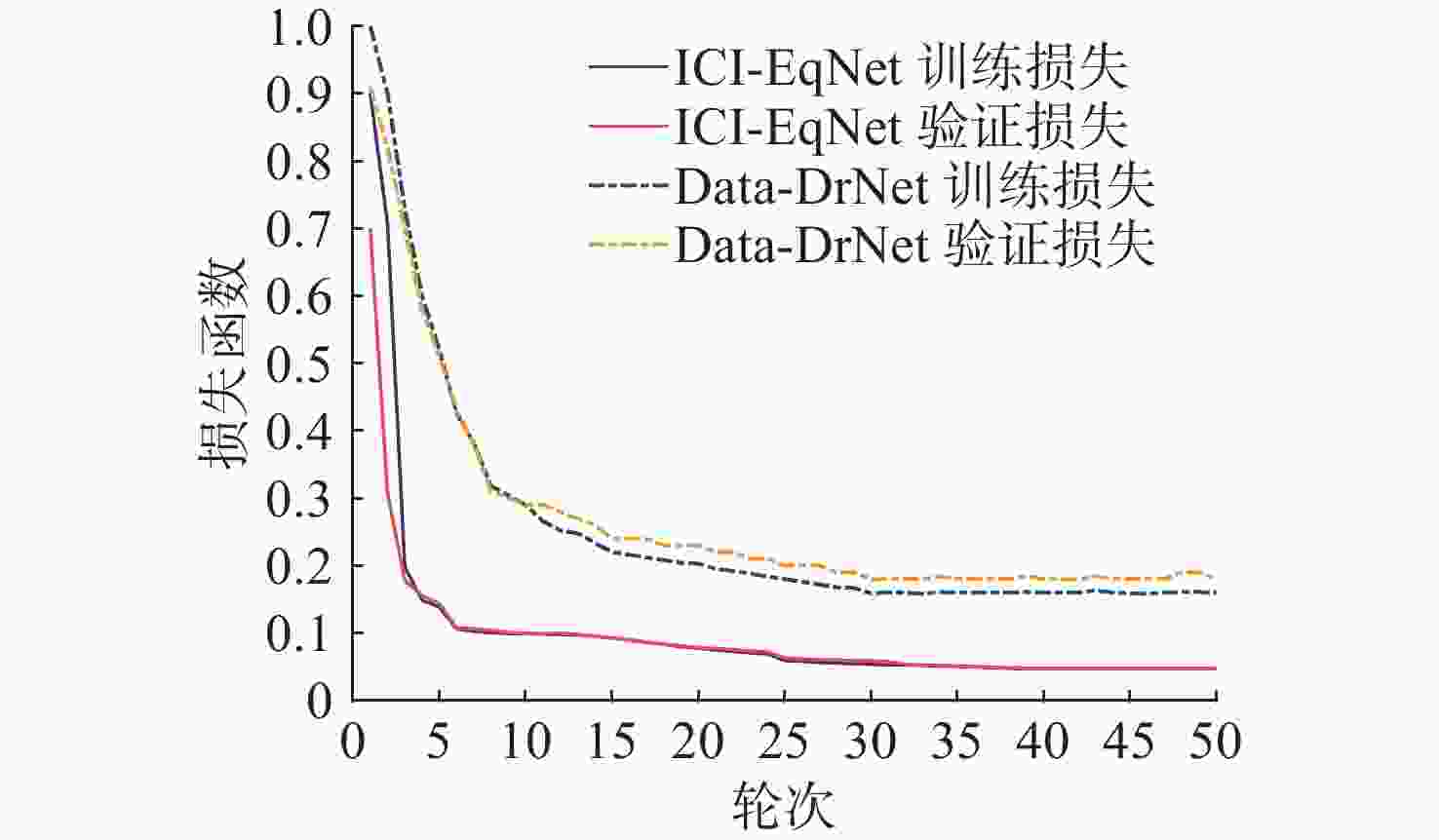
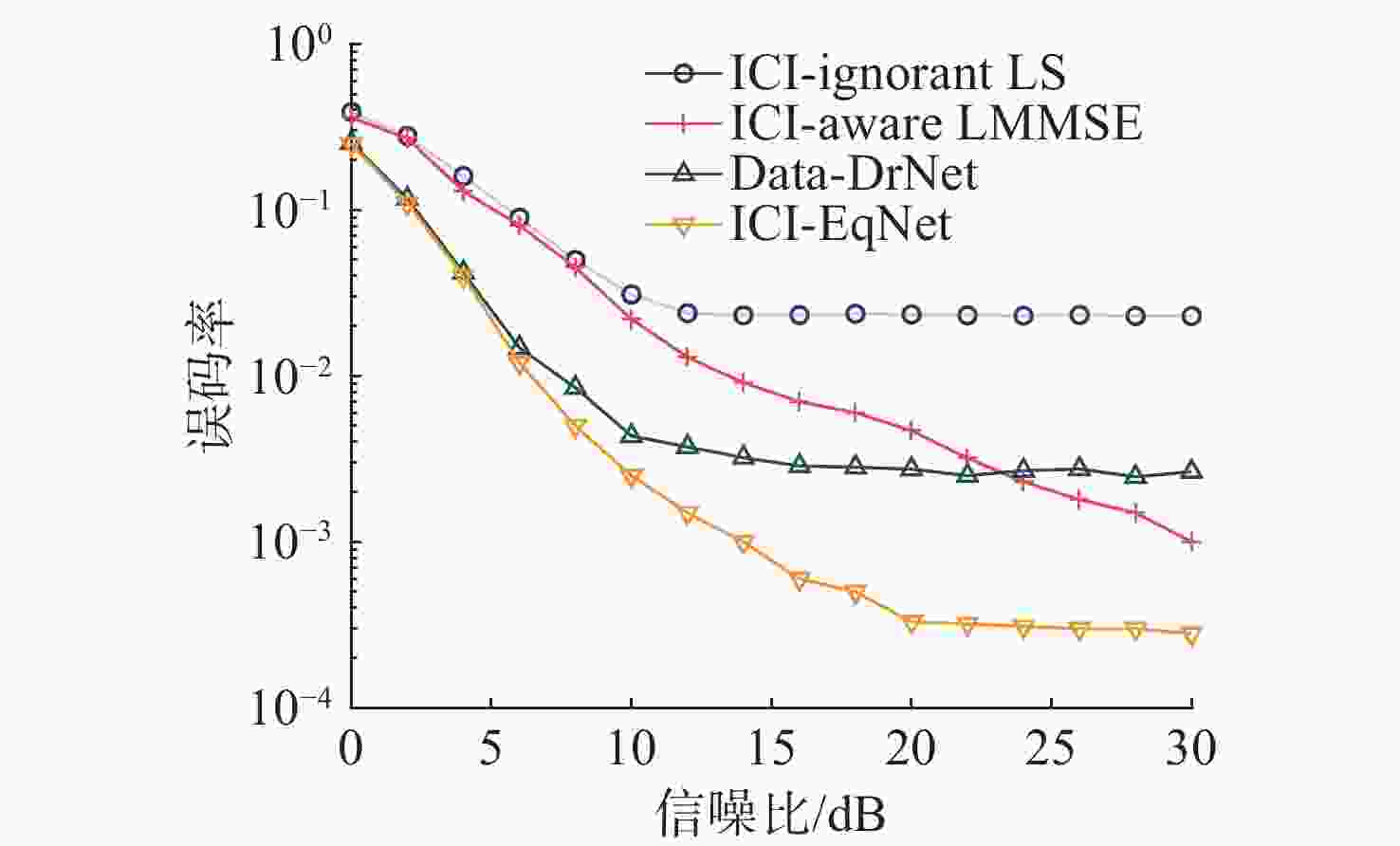
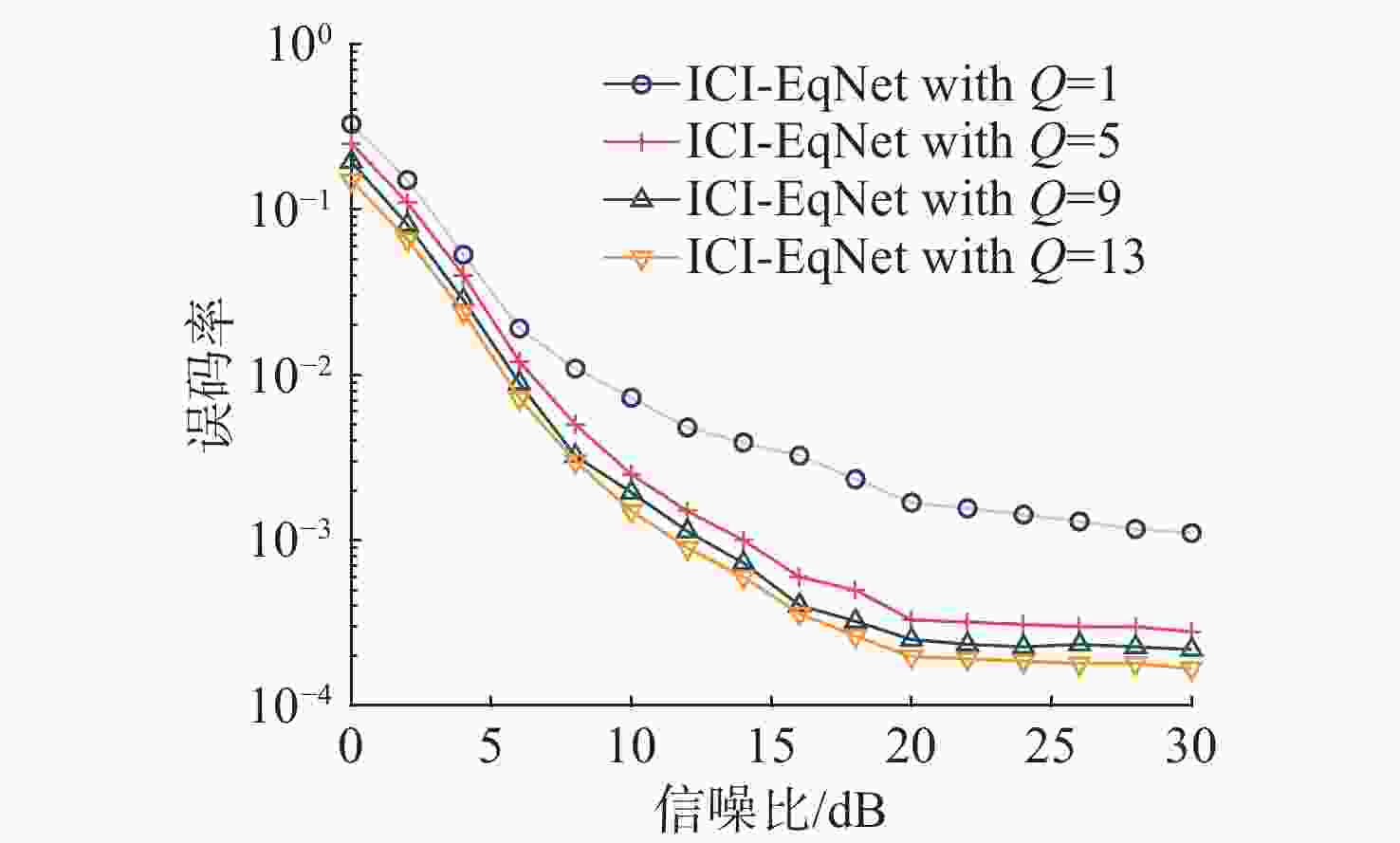
摘要: 以OFDM为代表的多载波通信是目前水声高谱效传输的主流体制, 可有效应对水声多路径传播带来的频率选择性衰落问题, 然而在快时变场景下的子载波间干扰(ICI)会严重影响传输可靠性。针对水声快变信道下的时间-频率双选择性衰落问题, 为了降低OFDM系统的接收误码率, 提出一种结合深度学习和领域知识的水声快变信道均衡方法, 不同于将传统信道估计和均衡检测结果作为深度神经网络(DNN)的预处理结果或者补充信息源, 文中使用经典频域均衡模型的结构化信息辅助DNN模型训练和推理, 以抵抗ICI的不利影响, 并适应实际部署信道环境与训练信道环境失配的场景。仿真和海上测试结果表明所提出方法能够有效降低接收机误码率, 能够实现更快的模型收敛速度, 并在未知信道条件下具有实现更强泛化性能的潜力。Abstract: Multicarrier communication schemes, such as Orthogonal Frequency Division Multiplexing (OFDM), are the mainstream solutions for achieving high spectral efficiency in underwater acoustic (UWA) transmissions. These schemes effectively address frequency-selective fading caused by multipath propagation in underwater environments. However, in rapidly time-varying scenarios, inter-carrier interference (ICI) can severely compromise transmission reliability. To mitigate the time-frequency doubly-selective fading in such UWA channels and reduce the bit error rate (BER) of OFDM systems, this paper proposes a novel channel equalization method that combines deep learning with domain knowledge. Rather than treating the outcomes of traditional channel estimation and equalization detection as preprocessing results or supplementary information sources for deep neural networks (DNNs), this paper employs the structured information from classical frequency-domain equalization models to assist in the training and inference of DNN models. This approach is designed to counteract the adverse effects of ICI and adapt to scenarios where there is a mismatch between the actual deployment channel environment and the training channel environment. Numerical simulation and sea trial results confirm that the proposed approach can effectively reduce the BER of the OFDM receivers, achieve faster model convergence, and has the potential to deliver stronger generalization performance under unknown channel conditions.
-
Key words:
- Underwater Acoustic Communication /
- Rapidly Time-Varying Channel /
- Deep Learning /
- OFDM
-
图 2 ICI-EqNet在OFDM接收机中的部署位置
Figure 2. The deployment position of ICI-EqNet in OFDM receivers
图 6 惠州海试水声通信设备
Figure 6. The UWA communication equipment used in the Huizhou sea trial
图 7 海试中收发端相距约4 600 m时的定位信息
Figure 7. The positioning information when the transmitter and receiver were approximately 4 600 meters apart during the sea trial
图 8 海试发送波形和时-频特性
Figure 8. Transmitted waveforms and time-frequency characteristics from the sea trial
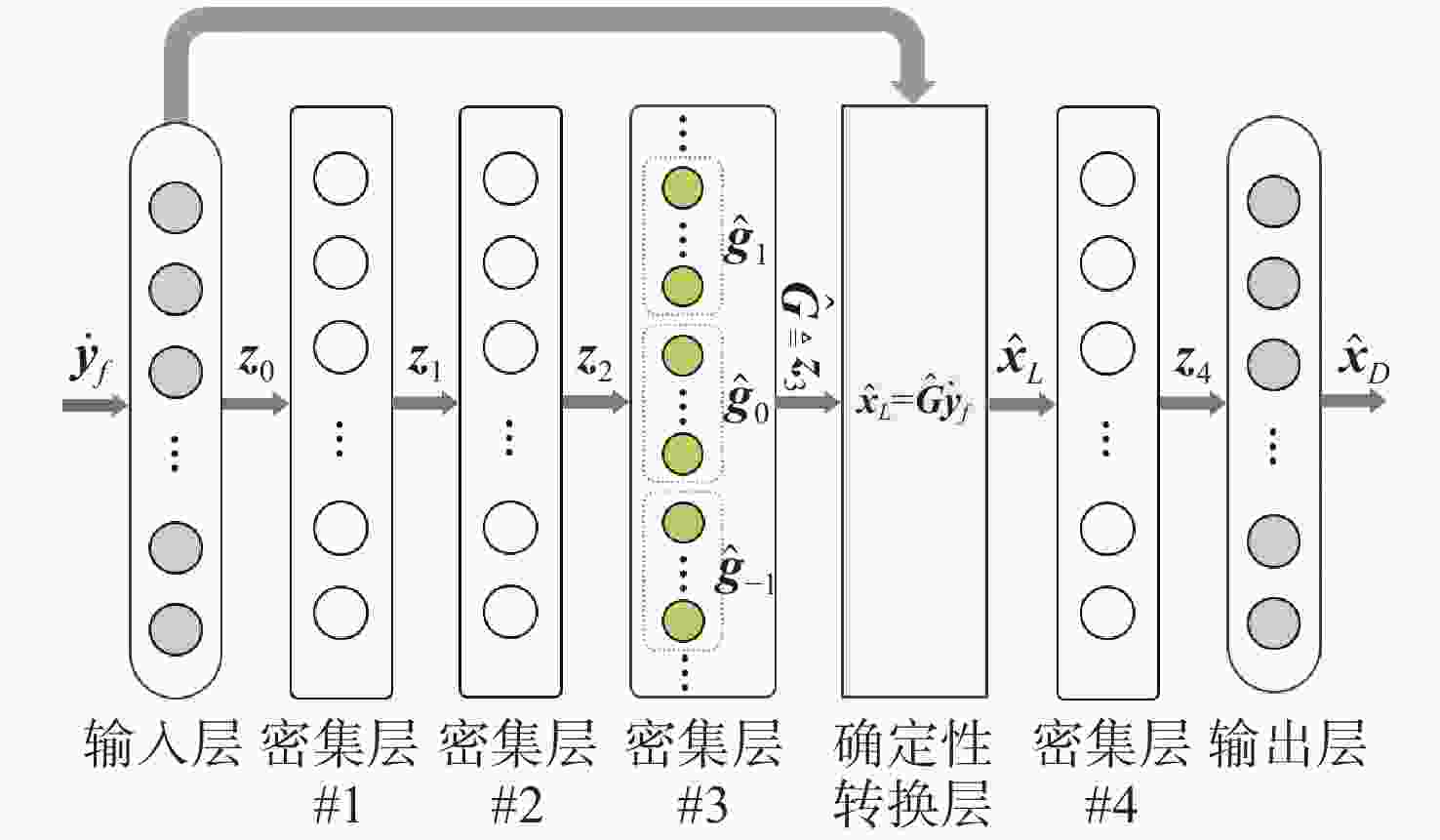
表 1 ICI-EqNet参数列表
Table 1. Parameters of ICI-EqNet
层标识 节点数 激活函数 输入层 $ 2\tilde N $ — 密集层#1 $ 2\tilde N $ ReLU 密集层#2 $ \tilde N $ ReLU 密集层#3 $ 2\dot NQ $ Linear 确定性转换层 $ 2\dot N $ — 密集层#4 $ 2\dot N $ tanh 输出层 $ 2{\dot N_D} $ tanh 
下载: 导出CSV
表 2 波形参数设计
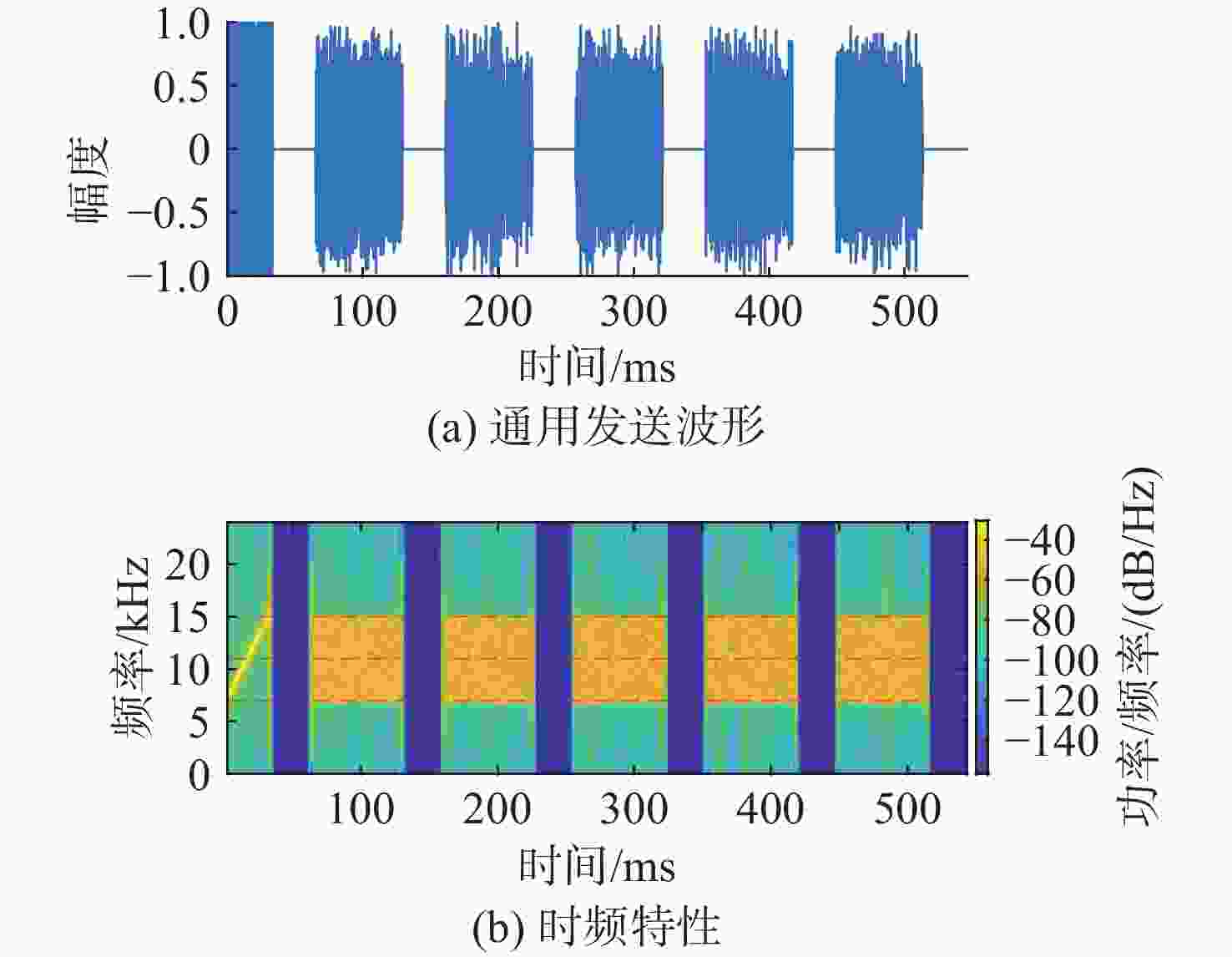
Table 2. Waveform Parameter Design
参数 标识 大小 中心频率/kHz $ {f_c} $ 11 占用带宽/kHz B 8 IFFT/FFT长度 N 1 024 活跃子载波数目 $ \dot N $ 512 导频子载波数目 $ {\dot N_P} $ 128 数目子载波数目 $ {\dot N_D} $ 384 基带采样周期/ms $ \Delta T = \dot N/(NB) $ 0.062 5 子载波间隔/Hz $ \Delta f = B/\dot N $ 15.625 基本符号周期/ms $ T = N\Delta T $ 64 保护间隔长度/ms $ {T_{ZP}} $ 16 完整符号周期/ms $ {T_s} = T + {T_{ZP}} $ 80
下载: 导出CSV
表 3 海试误码率比较
Table 3. Comparison of BER in the sea trial
收发
距离/m总帧数 LS
误码率/%LMMSE
误码率/%Data-DrNet
误码率/%ICI-EqNet
误码率/%590 503 0.170 0.059 0.093 0.052 1 700 506 1.248 0.634 0.194 0.093 4 600 502 6.129 5.202 0.913 0.130
下载: 导出CSV
-
[1] LI B, ZHOU S, STOJANOVIC M, et al. Multicarrier communication over underwater acoustic channels with nonuniform Doppler shifts[J]. IEEE Journal of Oceanic Engineering, 2008, 33(2): 198-209. doi: 10.1109/JOE.2008.920471 [2] BERGER C R, ZHOU S, PREISIG J C, et al. Sparse channel estimation for multicarrier underwater acoustic communication: from subspace methods to compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1708-21. doi: 10.1109/TSP.2009.2038424 [3] YU H, SONG A, BADIEY M, et al. Iterative estimation of doubly selective underwater acoustic channel using basis expansion models[J]. Ad Hoc Networks, 2015, 34(11): 52-61. [4] WANG S, LIU M, LI D. Bayesian learning-based clustered-sparse channel estimation for time-varying underwater acoustic OFDM communication[J]. Sensors, 2021, 21(14): 4889. doi: 10.3390/s21144889 [5] KANNU A P, SCHNITER P. Design and analysis of MMSE pilot-aided cyclic-prefixed block transmissions for doubly selective channels[J]. IEEE Transactions on Signal Processing, 2008, 56(3): 1148-1160. doi: 10.1109/TSP.2007.908969 [6] KALTENBERGER F, ZEMEN T, UEBERHUBER C W. Low-complexity doubly selective channel simulation using multidimensional discrete prolate spheroidal sequences[EB/OL]. [2024-12-13]. https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=764a2987979e1c69ff36f33bdf818c3763d4d5dc. [7] NEUMANN D, WIESE T, UTSCHICK W. Learning the MMSE channel estimator[J]. IEEE Transactions on Signal Processing, 2018, 66(11): 2905-2917. doi: 10.1109/TSP.2018.2799164 [8] YE H, LI G Y, JUANG B H F. Power of deep learning for channel estimation and signal detection in OFDM systems[J]. IEEE Wireless Communication Letters, 2017, 16(99): 114-117. [9] JIANG R, WANG X, CAO S, et al. Deep neural networks for channel estimation in underwater acoustic OFDM systems[J]. IEEE Access, 2019, 7(7): 23579-94. [10] ZHANG Y, LI J, ZAKHAROV Y, et al. Deep learning based underwater acoustic OFDM communications[J]. Applied Acoustics, 2019, 154(11): 53-58. [11] 赵昊. 基于深度学习的水声通信物理层技术研究[D]. 广州: 华南理工大学, 2023. [12] 张永霖, 王海斌, 李超, 等. 水声通信中的信道估计与机器学习交叉研究进展[J]. 声学技术, 2022, 41(3): 334-345. doi: 10.3969/j.issn.1000-3630.2022.3.sxjs202203005ZHANG Y L, WANG H B, LI C, et al. Advances in the intersection of channel estimation and machine learning in underwater acoustic communications[J]. Technical Acoustics, 2022, 41(3): 334-345. doi: 10.3969/j.issn.1000-3630.2022.3.sxjs202203005 [13] Chen Y, Qiao P, Ren X, et al. OFDM underwater acoustic communication receiver based on deep learning [C]//OCEANS. Singapore: IEEE, 2024. [14] Shlezinger N, Whang J, Eldar Y C, et al. Model-based deep learning: Key approaches and design guidelines[C]//IEEE Data Science and Learning Workshop (DSLW). Toronto, Canada: IEEE, 2021. [15] XU Z B, SUN J. Model-driven deep-learning[J]. National Science Review, 2018, 5(1): 22-24. doi: 10.1093/nsr/nwx099 [16] Lin X, Shen Y, C. Jiang. A Model-driven deep learning-based receiver for OFDM system with carrier frequency offset[J]. IEEE Communications Letters, 2024, 28(4): 813-817. doi: 10.1109/LCOMM.2024.3354990 [17] FENG X, ZHOU M, WANG J, SUN H, et al. Model-driven deep learning-based estimation for underwater acoustic channels with uncertain sparsity[J]. IEEE Transactions on Wireless Communications, 2024, 23(6): 5710-25. doi: 10.1109/TWC.2023.3327995 [18] GAO X, JIN S, WEN C K, et al. ComNet: Combination of deep learning and expert knowledge in OFDM receivers[J]. IEEE Communications Letters, 2018, 22(12): 2627-30. doi: 10.1109/LCOMM.2018.2877965 [19] RU X, WEI L, XU Y. Model-driven channel estimation for OFDM systems based on image super-resolution network[C]//2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP). Nanjing, China: IEEE, 2020. [20] ZHAO H, JI F, WEN M, et al. Multi-task learning based underwater acoustic OFDM communications[C]//2021 IEEE International Conference on Signal Processing, Communications and Computing. Xi’an, China: IEEE, 2021. [21] MUQUET B, WANG Z, GIANNAKIS G B, et al. Cyclic prefixing or zero padding for wireless multicarrier transmissions?[J]. IEEE Transactions on Communications, 2002, 50(12): 2136-48. doi: 10.1109/TCOMM.2002.806518 [22] GOLUB G H , VAN LOAN C F. Matrix Computations [M]. 4th ed. Baltimore, MD: Johns Hopkins University Press, 2013. [23] HLAWATSCH F, MATZ G. Wireless communications over rapidly time-varying channels[M]. New York: Academic Press, 2011. -
点击查看大图
图(8) / 表(3)
计量
- 文章访问数: 20
- HTML全文浏览量: 9
- PDF下载量: 2
- 被引次数: 0
