Prediction Method for Buckling of Deep-Water Explosion Cylindrical Shell Based on Random Forest
-
摘要: 在深水爆炸条件下, 圆柱壳等耐压结构会出现与浅水环境下不同的失效模式, 即失稳屈曲。为研究圆柱壳结构在深水爆炸条件下发生失稳屈曲的条件, 实现对其屈曲状态的预测, 首先建立了数值仿真模型, 对不同药量、爆距和水深条件下的圆柱壳屈曲结果进行了仿真分析。基于仿真结果, 设计了随机森林模型对屈曲状态进行了预测。结果表明, 在深水环境轴向爆炸的加载条件下, 基于随机森林算法构建的预测模型可以较好地实现对特定结构参数下圆柱壳失稳状态的预测, 2种结构下的预测准确率分别达到了93.75%和87.5%, 并对药量、爆距和静压强度3种特征对结构状态影响的重要性程度进行了评价, 可为圆柱壳屈曲条件研究提供参考。Abstract: Under deep-water explosion conditions, pressure-resistant structures such as cylindrical shells will have a different failure mode from that in a shallow water environment, namely, instability buckling. In order to study the conditions for the occurrence of instability buckling of cylindrical shells under deep water explosion conditions and predict the buckling state, a numerical simulation model was first established to simulate and analyze the results of the buckling of cylindrical shells under the conditions of different charge amounts, blast distance, and water depths. Based on the simulation results, a random forest model was designed to predict the buckling state. The results show that under the loading conditions of axial explosion in a deep water environment, the prediction model constructed based on the random forest algorithm can effectively predict the unstable state of cylindrical shells under specific structural parameters. The prediction accuracy rates for the two structures reach 93.75% and 87.5%, respectively. The importance of the three characteristics, charge amount, blast distance, and static pressure strength, in influencing the structural state is evaluated. This can provide a reference for the study of the buckling conditions of cylindrical shells.
-
Key words:
- deep-water explosion /
- buckling /
- random forest /
- cylindrical shell
-
图 4 500 m水深下圆柱壳变形情况图
Figure 4. Deformation diagram of cylindrical shell at a depth of 500 m
图 5 特定工况下圆柱壳失稳屈曲过程
Figure 5. Buckling process of cylindrical shell under specific working conditions
图 6 不同条件下失稳屈曲状态分布
Figure 6. Distribution of unstable buckling states under different conditions
图 11 改变结构参数后的预测结果混淆矩阵
Figure 11. Confusion matrix of prediction results after changing structural parameters
图 12 改变结构参数后的预测结果ROC曲线图
Figure 12. ROC curve of prediction results after changing structural parameters
图 13 改变结构参数后的特征重要性得分
Figure 13. Feature importance score after changing structural parameters
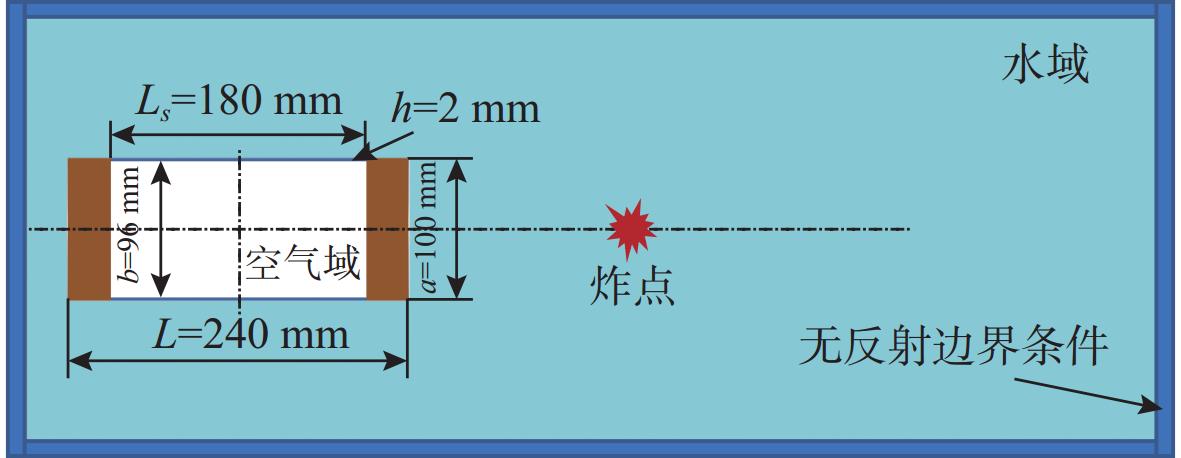
表 1 模型几何尺寸参数
Table 1. Geometric dimension parameters of the model
参数 符号 数值 外径/mm $ a $ 100 内径/mm $ b $ 96 厚度/mm $ h $ 2 壳体段长度/mm $ {L_s} $ 180 端盖半径/mm $ R $ 50 端盖长度/mm $ {L_c} $ 30 总长度/mm $ L $ 240 
下载: 导出CSV
表 2 水的材料参数
Table 2. Material properties of water
$ {C_0^{\mathrm{w}}} $ $ {C_1^{\mathrm{w}}} $ $ {C_2^{\mathrm{w}}} $ $ {C_3^{\mathrm{w}}} $ $ {C_4^{\mathrm{w}}} $ $ {C_5^{\mathrm{w}}} $ $ {C_6^{\mathrm{w}}} $ $ {E_0^{\mathrm{w}}}/\mathrm{Pa} $ 0 2.2×109 9.54×109 1.457×109 0.28 0.28 0 2.136×107
下载: 导出CSV
表 3 空气材料参数
Table 3. Material properties of air
$ {C_0^{\mathrm{a}}} $ $ {C_1^{\mathrm{a}}} $ $ {C_2^{\mathrm{a}}} $ $ {C_3^{\mathrm{a}}} $ $ {C_4^{\mathrm{a}}} $ $ {C_5^{\mathrm{a}}} $ $ {C_6^{\mathrm{a}}} $ $ {E_0^{\mathrm{a}}}/\mathrm{Pa} $ 0.0 0.0 0.0 0.0 0.4 0.4 0.0 253200
下载: 导出CSV
表 4 JWL方程参数
Table 4. Parameters of JWL equation
$ \rho /({\mathrm{kg}} \cdot {{\mathrm{m}}^{ - 3}}) $ $ A/{\mathrm{Pa}} $ $ B/{\mathrm{Pa}} $ $ {R_1} $ $ {R_2} $ $ w $ $ E_v/\mathrm{Pa} $ 1630 3.738×1011 3.747×109 4.15 0.9 0.35 6×109
下载: 导出CSV
表 5 6061铝合金参数
Table 5. Parameters of 6061 aluminum alloy
$ \rho_1 /({\mathrm{kg}} \cdot {{\mathrm{m}}^{ - 3}}) $ $ E/{\mathrm{GPa}} $ $ {\sigma _Y}/{\mathrm{MPa}} $ $ {E_{\tan }}/{\mathrm{MPa}} $ $ \upsilon $ 2690 70 276 646 0.33
下载: 导出CSV
表 6 静压加载下圆柱壳失稳屈曲情况
Table 6. Buckling instability of cylindrical shells under static pressure loading
H/m 失稳情况 600 未失稳屈曲 620 未失稳屈曲 640 未失稳屈曲 660 失稳屈曲 680 失稳屈曲 700 失稳屈曲
下载: 导出CSV
表 7 设计工况表
Table 7. Designed working conditions
$ H $/m $ \omega $/g $ \gamma $ 600 1、5、10、20 15、20、30、40、50 550 1、5、10、20 15、20、30、40、50 500 1、5、10、20 15、20、30、40、50 400 1、5、10、20 15、20、30、40、50
下载: 导出CSV
表 8 圆柱壳失稳屈曲状态预测结果
Table 8. Prediction results of unstable buckling state of cylindrical shell
序号 真实类 预测类 1 未屈曲 未屈曲 2 未屈曲 未屈曲 3 未屈曲 未屈曲 4 未屈曲 未屈曲 5 未屈曲 未屈曲 6 未屈曲 未屈曲 7 未屈曲 未屈曲 8 未屈曲 未屈曲 9 未屈曲 未屈曲 10 未屈曲 未屈曲 11 屈曲 屈曲 12 屈曲 屈曲 13 屈曲 屈曲 14 屈曲 屈曲 15 屈曲 屈曲 16 屈曲 未屈曲
下载: 导出CSV
表 9 外插工况表
Table 9. Working conditions of external plug-in
$ H $/m $ \omega $/g $ \gamma $ 真实类 预测类 580 7.5 20 屈曲 屈曲 560 12 20 屈曲 屈曲 540 4 30 未屈曲 未屈曲 520 15 20 屈曲 屈曲 500 12 15 屈曲 未屈曲 480 8 30 未屈曲 未屈曲 460 18 30 屈曲 屈曲 440 11 40 未屈曲 未屈曲 420 6 20 未屈曲 未屈曲 400 3 40 未屈曲 未屈曲
下载: 导出CSV
表 10 改变结构参数后的模型几何尺寸参数
Table 10. Geometric dimension parameters of the model after changing structural parameters
参数 符号 数值 外径/mm $ a $ 140 内径/mm $ b $ 134 厚度/mm $ h $ 3 壳体段长度/mm $ {L_s} $ 200 端盖半径/mm $ R $ 50 端盖长度/mm $ {L_c} $ 30 总长度/mm $ L $ 260
下载: 导出CSV
表 11 改变结构参数后的仿真工况表
Table 11. Simulation conditions after changing structural parameters
$ H $/m $ \omega $/g $ \gamma $ 900 1、5、10、20 15、20、30、40、50 800 1、5、10、20 15、20、30、40、50 700 1、5、10、20 15、20、30、40、50 600 1、5、10、20 15、20、30、40、50
下载: 导出CSV
表 12 改变结构参数后的圆柱壳失稳屈曲状态预测结果
Table 12. Prediction results of unstable buckling state of cylindrical shell after changing structural parameters
序号 真实类 预测类 1 未屈曲 未屈曲 2 未屈曲 未屈曲 3 未屈曲 未屈曲 4 未屈曲 未屈曲 5 未屈曲 未屈曲 6 未屈曲 未屈曲 7 未屈曲 未屈曲 8 未屈曲 未屈曲 9 未屈曲 未屈曲 10 未屈曲 未屈曲 11 屈曲 屈曲 12 屈曲 屈曲 13 屈曲 屈曲 14 屈曲 屈曲 15 屈曲 屈曲 16 屈曲 未屈曲
下载: 导出CSV
表 13 2次预测的准确率与AUC
Table 13. The accuracy and AUC of two predictions
模型序号 总工况数 预测准确率/% AUC 1 80 93.75 0.92 2 80 87.50 0.87
下载: 导出CSV
-
[1] COLE R H. Underwater explosion[M]. Princeton, NJ, US: Princeton University Press, 1948. [2] GAO Y, WANG S, ZHANG J, et al. Effects of underwater explosion depth on shock wave overpressure and energy[J]. Physics of Fluids, 2022, 34(3): 037108. doi: 10.1063/5.0081107 [3] 王树山. 终点效应学[M]. 北京: 科学出版社, 2019. [4] WINDENBURG D F, TRILLING C. Collapse by instability of thin cylindrical shells under external pressure[J]. Transactions of the American Society of Mechanical Engineers, 1934, 56(8): 819-825. doi: 10.1115/1.4019870 [5] 董金鑫, 黄伟佳, 宋丹丹, 等. 深水爆炸作用下耐压圆柱壳的稳定性研究[J]. 舰船电子工程, 2024, 44(5): 147-152. doi: 10.3969/j.issn.1672-9730.2024.05.029DONG J X, HUANG W J, SONG D D, et al. Research on stability of pressure cylindrical shell under deep water explosion[J]. Ship Electronic Engineering, 2024, 44(5): 147-152. doi: 10.3969/j.issn.1672-9730.2024.05.029 [6] GUPTA S, MATOSA H, LEBLANC J M, et al. Shock initiated instabilities in underwater cylindrical structures[J]. Journal of the Mechanics and Physics of Solids, 2016(5): 188-212. [7] SUN W, ZHU T, CHEN P, et al. Dynamic implosion of submerged cylindrical shell under the combined hydrostatic and shock loading[J]. Thin-Walled Structures, 2022, 170: 108574. doi: 10.1016/j.tws.2021.108574 [8] 贾宪振. 基于通用程序的水下爆炸及其对结构作用的数值模拟研究[D]. 南京: 南京理工大学, 2008. [9] 辛春亮. 有限元分析常用材料参数手册[M]. 北京: 机械工业出版社, 2022. [10] LEE E, FINGER M, COLLINS W. JWL Equation of state coefficients for high explosives[M]. Lawrence: Lawrence Livermore Laboratory, 1973. [11] BOUAMOUL A, BOLDUC M. Characterization of Al 6061-T6 using split Hopkinson bar tests and numerical simulations[C]//22nd International Symposium of Ballistics. Vancouver. Canada: IBC, 2005: 1063-1070 . [12] 吴浩岩. 深水近场爆炸对圆筒结构的毁伤效应研究[D]. 北京: 北京理工大学, 2023. [13] 李德聪, 郑绍文, 吴国民. 关于水下中远场爆炸相似律与冲击因子的讨论[J]. 兵工学报, 2015, 36(S1): 46-52.LI D C, ZHENG S W, WU G M. Discussion on underwater mid and far-field explosion similarity laws and impulsive factor[J]. Acta Armamentarii, 2015, 36(S1): 46-52. -
点击查看大图
计量
- 文章访问数: 60
- HTML全文浏览量: 24
- PDF下载量: 1
- 被引次数: 0
