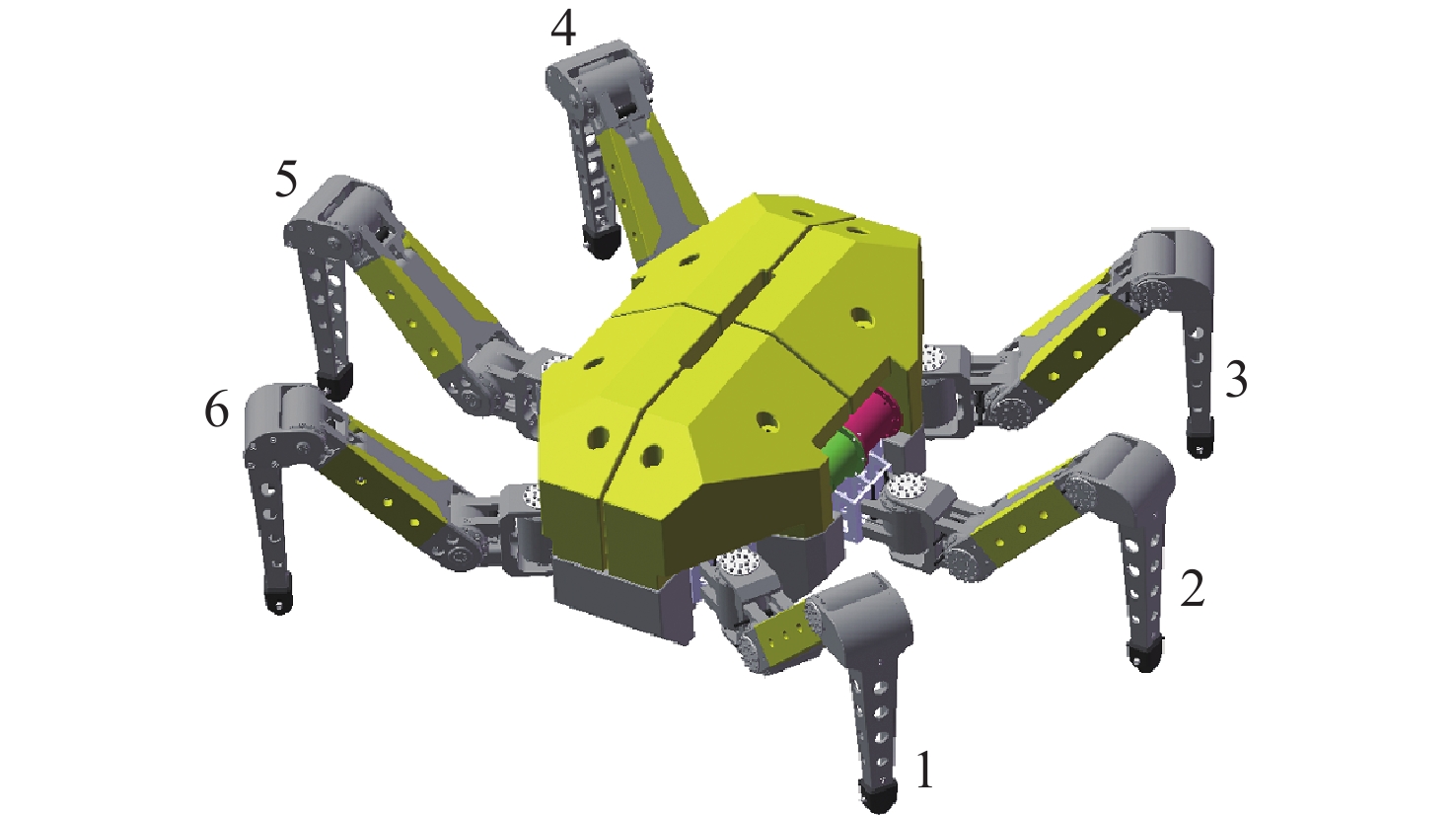
Control System for Underwater Hexapod Robot Based on Inverse Kinematics and Foot Trajectory Optimization
-
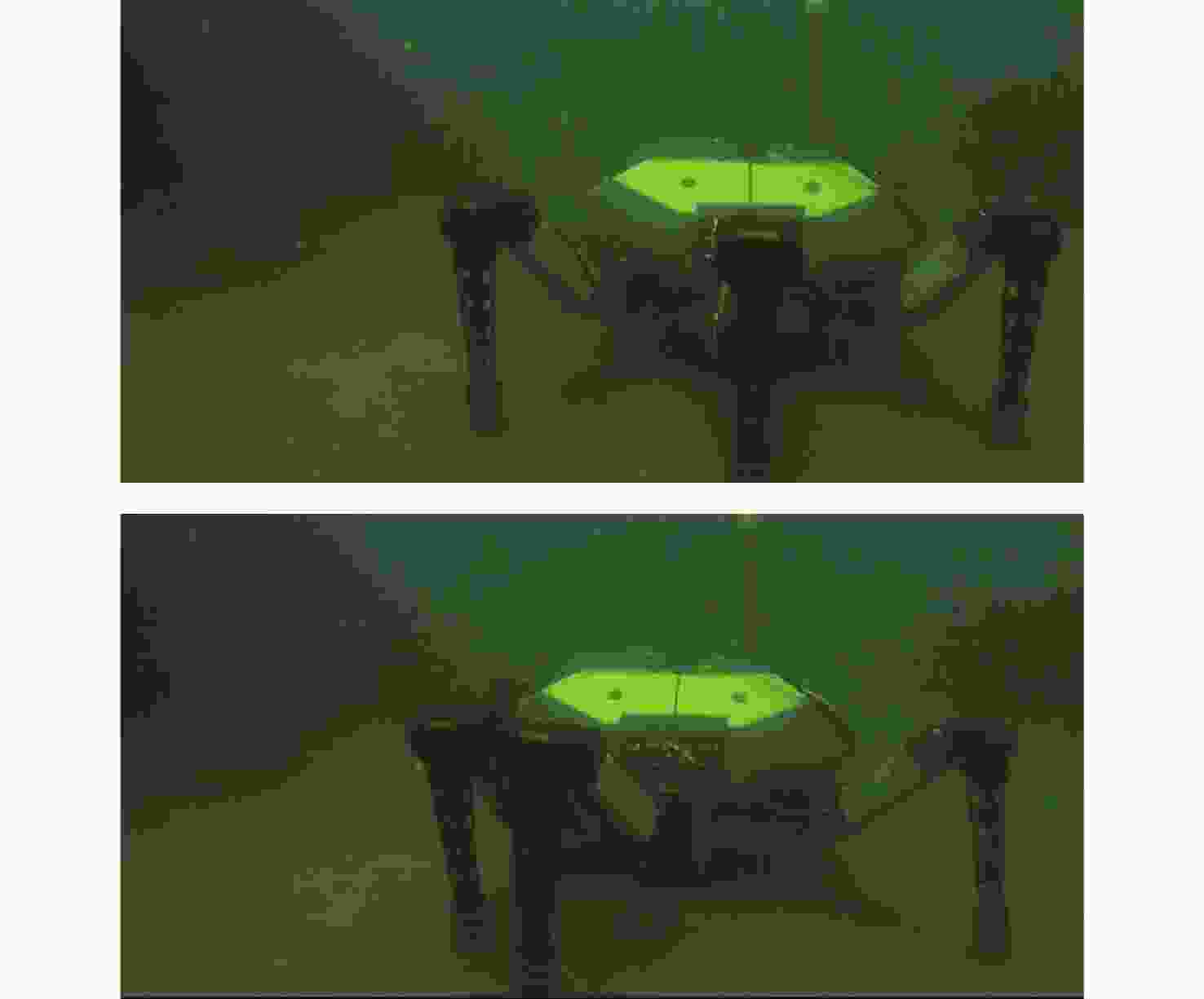
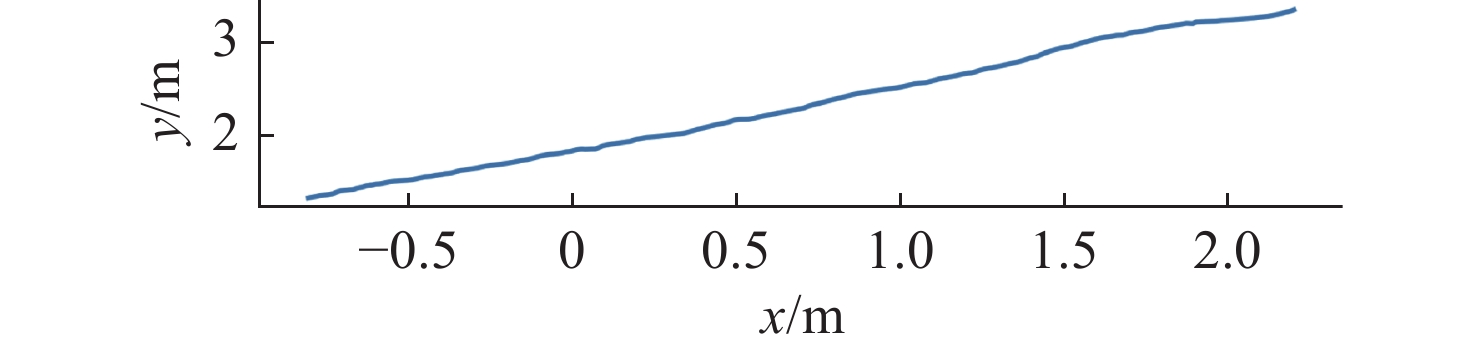
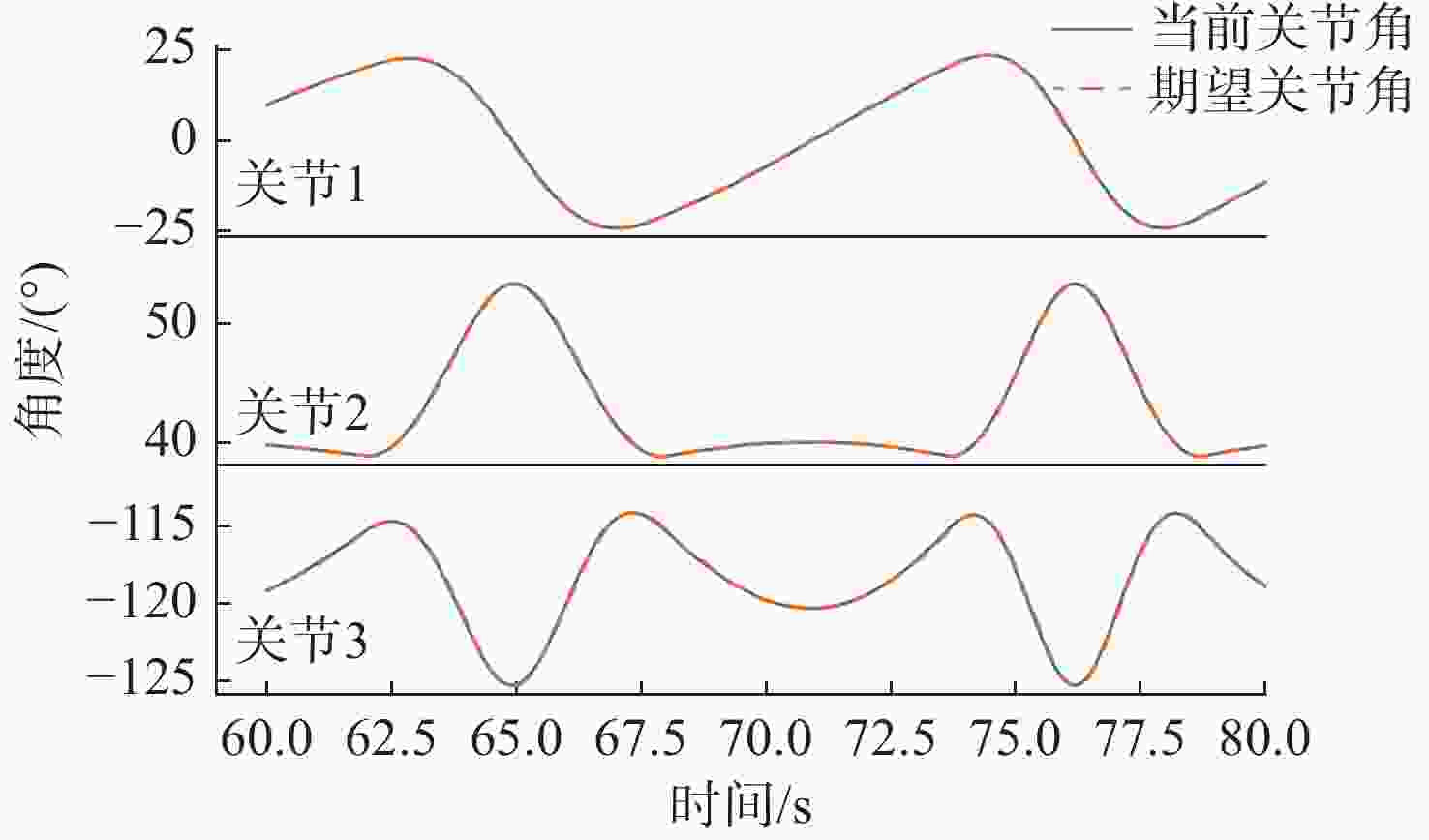
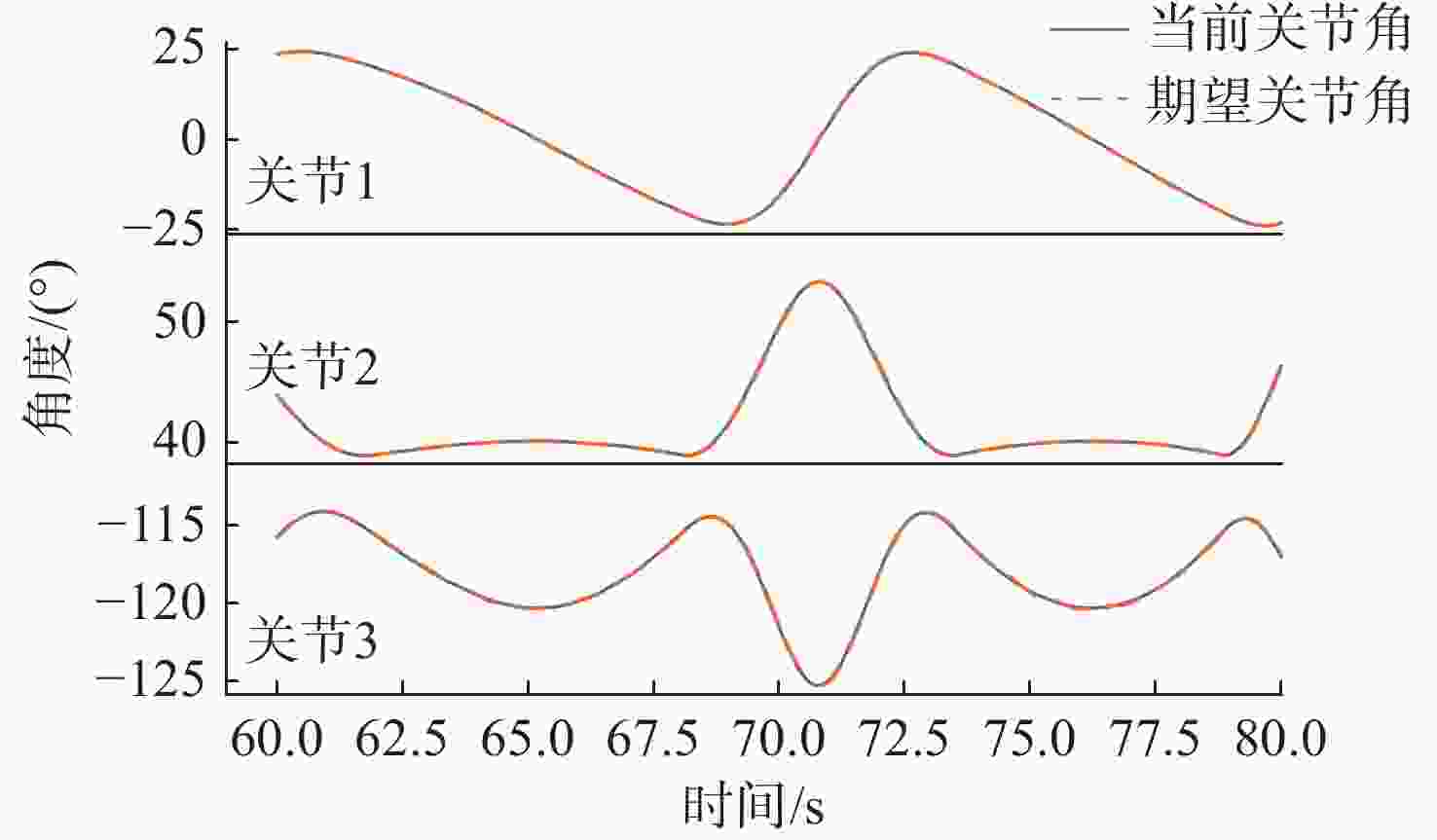
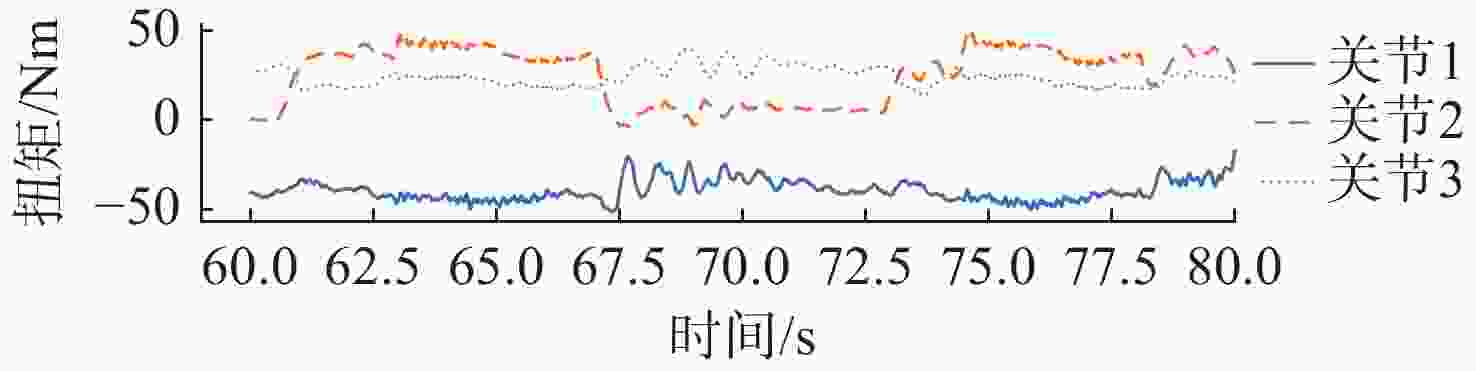
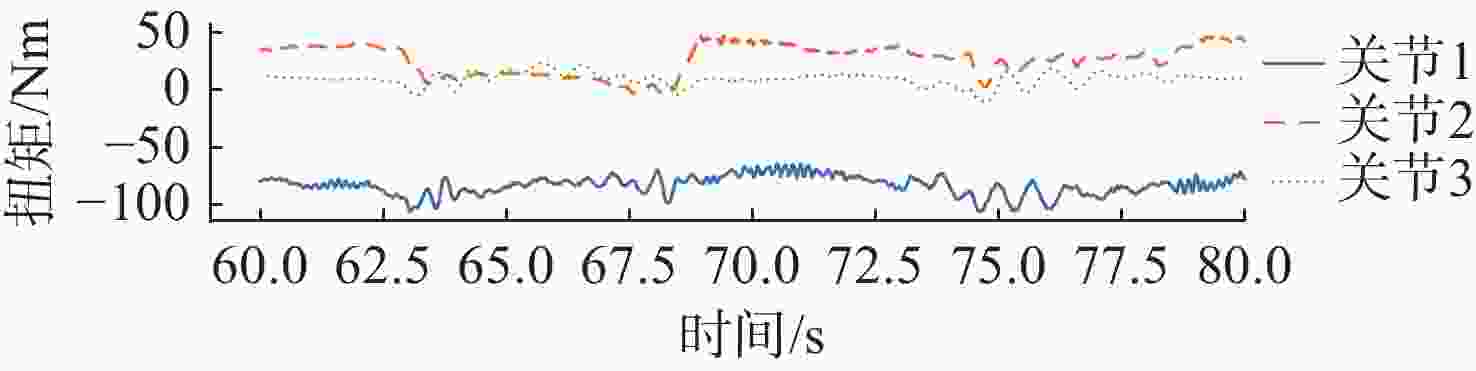
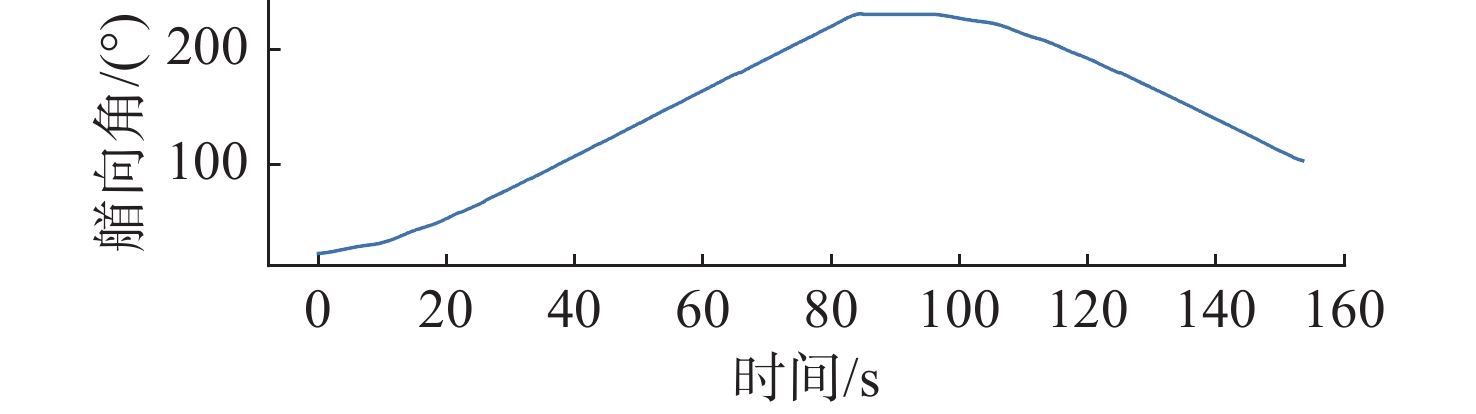
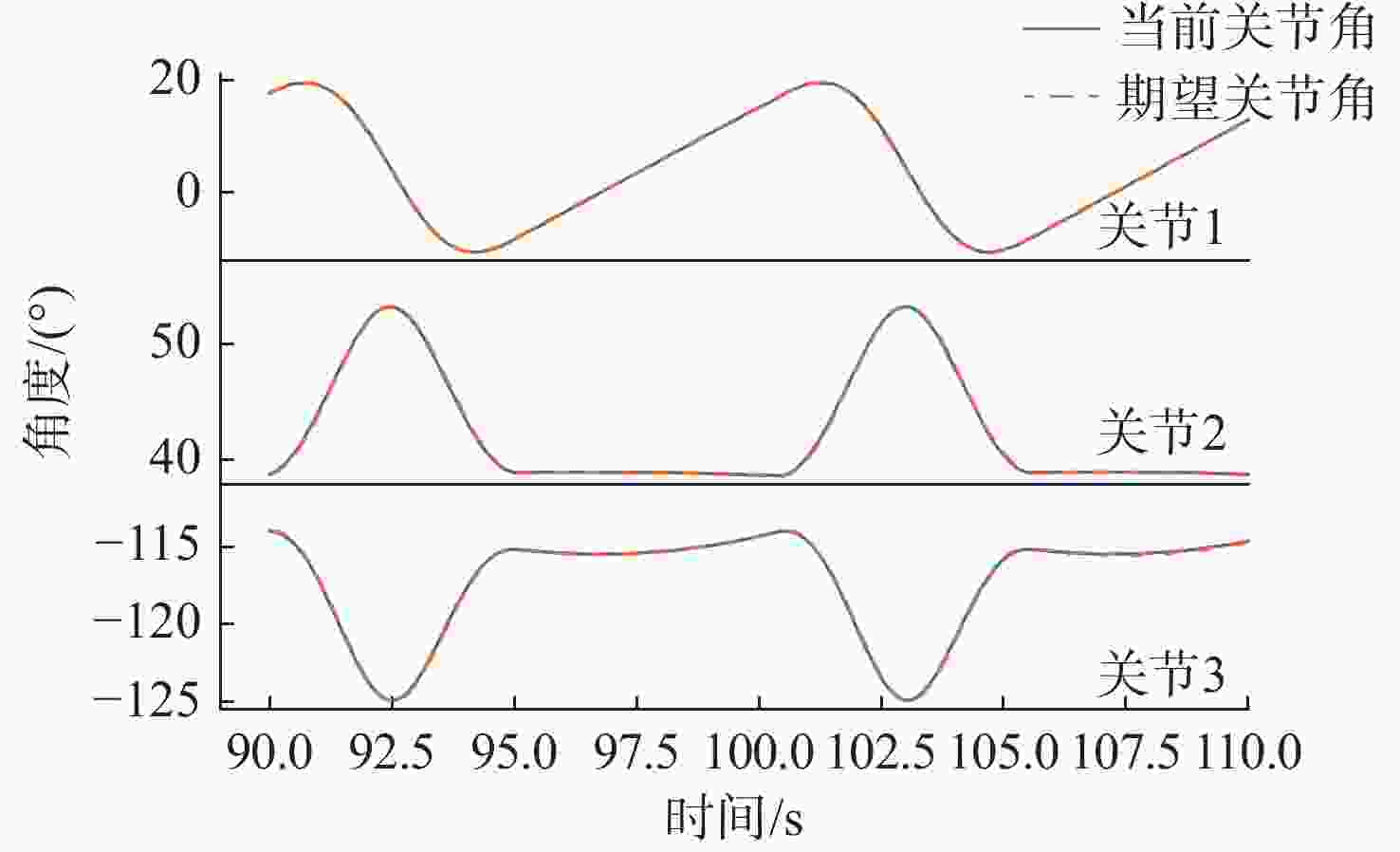
摘要: 水下六足机器人具有强带负载能力和地形适应能力, 非常适合在复杂多变的海底环境进行近地观测和采样。控制系统是实现水下六足机器人稳定行走的关键技术。文中提出了基于逆运动学和足端轨迹优化的水下六足机器人控制系统设计方法。建立D-H坐标系, 推导出足端轨迹与关节角之间的解析关系(正运动学); 通过多项式优化的方式规划出平滑的足端轨迹, 进而求解出对应的关节角(逆运动学); 以PC104为主控单元, 在ROS2环境中进行足端轨迹优化和逆运动学求解, 通过EtherCAT技术实现关节电机的同步跟踪, 设计出适用于水下六足机器人的控制系统。在水池中对水下六足机器人的典型运动方式(直行和转动)进行了验证，实验结果表明, 文中设计的控制系统可以实现水下六足机器人的稳定行走。Abstract: The underwater hexapod robot has a strong load carrying ability and terrain adaptability, which is very suitable for near-earth observation and sampling in complex and changeable seabed environments. The control system is the key technology to realize the stable walking of underwater hexapod robots. In this paper, a control system design method for underwater hexapod robots based on inverse kinematics and foot trajectory optimization was proposed. The D-H coordinate system was established to derive the analytical relationship between the foot trajectory and the joint angle(positive kinematics). Through polynomial optimization, a smooth foot trajectory was planned, and then the corresponding joint angle(inverse kinematics) was solved. With PC104 as the main control unit, the foot trajectory optimization and inverse kinematics solving were conducted in the ROS2 environment, and the synchronous tracking of the joint motor was realized through EtherCAT technology. The control system suitable for underwater hexapod robots was designed. The typical movement patterns(straight and turning) of the underwater hexapod robot were verified in the pool. Experimental results show that the control system designed in this paper can realize the stable walking of the underwater hexapod robot.
-
0. 引言
传统的浮动式水下机器人近地观测能力略显不足[1-2], 携带负载能力偏弱[3-4]。水下爬行机器人作为陆地爬行机器人的衍生形式, 具有较强的带负载能力和地形适应能力, 能够在行走过程中对海底进行近距离观测[5]。
水下六足机器人的研究包括机械结构、驱动机构、行走步态和控制系统等[6-7]。其中, 控制系统是水下六足机器人稳定行走的关键技术。水下六足机器人是由腿和身体组成的多刚体系统, 对其进行控制系统设计是一项具有挑战性的工作。文献[5-8]提出了基于虚拟力的控制算法, 即忽略腿部质量对身体重心的影响, 将身体重心的轨迹跟踪误差映射为重心处的虚拟力, 根据力和力矩平衡方程求解出所需的关节力矩。文献[9-11]在复杂地形环境中的稳定行走问题进行了研究, 通过调整身体和腿之间的相对位置关系对足端力进行补偿。由于水动力的影响, 水下六足机器人的控制问题更为复杂。王心亮等[12]对水下爬游机器人足端运动空间进行了分析。Wang等[5]研究了水下六足机器人的坐底问题。Davliakos等[13]设计了一款液压驱动六足机器人。
文中采用基于逆运动学和足端轨迹优化的控制策略, 根据指令和身体位姿规划出身体重心轨迹, 对摆动腿足端轨迹进行优化, 进而求解出满足关节电机跟踪要求的期望关节角; 通过以太网控制自动化技术(Ether control automation technology, EtherCAT)将期望关节角实时发送给关节电机; 关节电机内置比例-积分-微分(proportional-integral-derivative, PID)控制器的参数在机器人操作系统(robot operating system, ROS)环境下通过EtherCAT发送给关节电机, 实现关节角的精确跟踪; 最终, 实现了水下六足机器人的稳定行走。
1. 水下六足机器人运动学建模
水下六足机器人身体采用密封设计, 电控和通信系统安装在舱体内部, 如图1所示。每条机械腿有3个自由度, 机械腿第3个关节采用弯曲设计, 以增加关节运动幅度和承载能力。每个关节安装1台经过密封的关节电机。身体和腿通过水密接插件实现信号传输。底盘轮廓为对称不规则的六边形, 每条机械腿的跟关节与六边形连接, 腿的编号分别为1~6号。
1.1 正运动学
以2号和5号腿为例, 建立D-H(Denavit-Hartenberg)坐标系, 如图2所示, 其对应的D-H参数见表1。
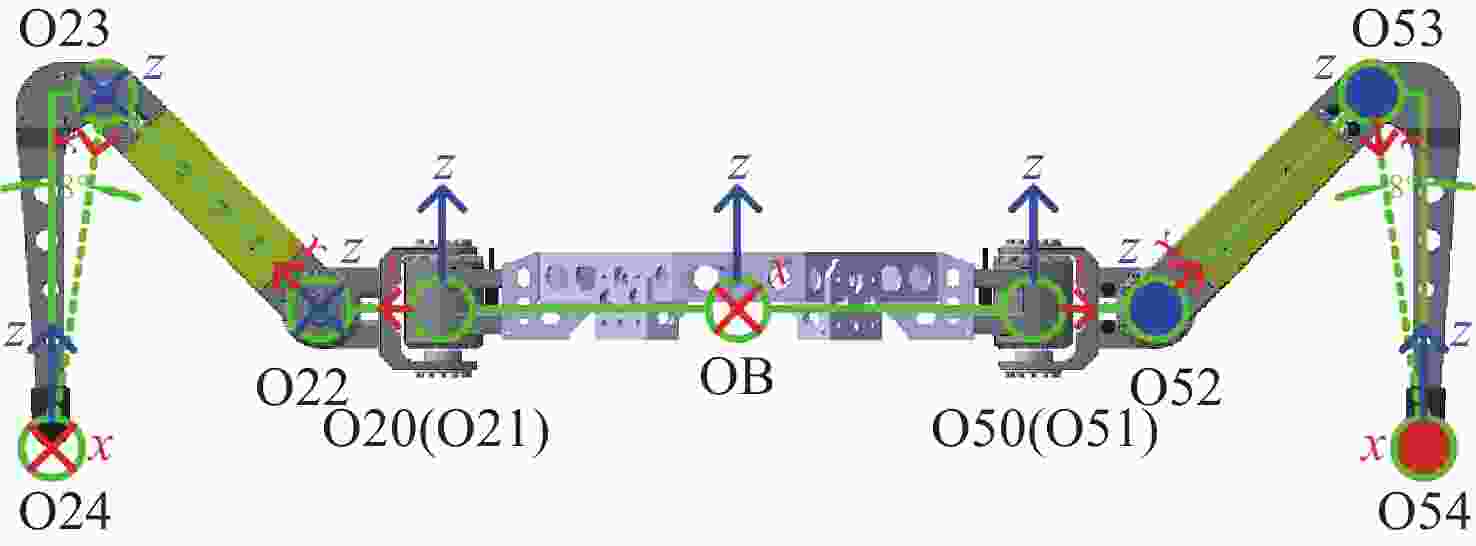
表 1 机械腿D-H参数表Table 1. D-H parameters of mechanical legi ${a_{j\left( {i - 1} \right)}}/{\text{m}}$ ${\alpha _{j\left( {i - 1} \right)}}/({\text{°}})$ ${d_{ji}}/{\text{m}}$ ${\theta _{ji}}/({\text{°}} )$ 0 ${l_{j{\text{0}}}}$ 0 0 ${\theta _{j{\text{0}}}}$ 1 0 0 0 ${\theta _{j1}}$ 2 ${l_{j1}}$ $90$ 0 ${\theta _{j2}}$ 3 ${l_{j2}}$ 0 0 ${\theta _{j3}}$ 4 ${l_{j3}}$ 0 0 0 坐标系
$\left\{ i \right\}$ 相对于坐标系$\left\{ {i - 1} \right\}$ 的齐次变换矩阵可以表示为$$ {\begin{gathered} {}_{i - 1}^i{{\boldsymbol{T}}_j} = \\ \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{ji}}} & { - \sin {\theta _{ji}}} & 0 & {{a_{j(i - 1)}}} \\ {\sin {\theta _{ji}}\cos {\alpha _{j(i - 1)}}} & {\cos {\theta _{ji}}\cos {\alpha _{j(i - 1)}}} & { - \sin {\alpha _{j(i - 1)}}} & { - \sin {\alpha _{j(i - 1)}}{d_{ji}}} \\ {\sin {\theta _{ji}}\sin {\alpha _{j(i - 1)}}} & {\cos {\theta _{ji}}\sin {\alpha _{j(i - 1)}}} & {\cos {\alpha _{j(i - 1)}}} & {\cos {\alpha _{j(i - 1)}}{d_{ji}}} \\ 0 & 0 & 0 & 1 \end{array}} \right] \\ \end{gathered}} $$ (1) 式中:
$ {a_{j\left( {i - 1} \right)}} $ 表示坐标系$ \{ {{O_{j\left( {i - 1} \right)}}} \} $ 的z轴与坐标系$ \{ {{O_{ji}}} \} $ 的z轴之间的距离;$ {\alpha _{j\left( {i - 1} \right)}} $ 表示坐标系$ \{ {{O_{j\left( {i - 1} \right)}}} \} $ 的z轴与坐标系$ \{ {{O_{ji}}} \} $ 的z轴之间的夹角;$ {d_{ji}} $ 表示坐标系$ \{ {{O_{j\left( {i - 1} \right)}}} \} $ 的x轴与坐标系$ \{ {{O_{ji}}} \} $ 的x轴在坐标系$ \{ {{O_{ji}}} \} $ 的z轴上的截距;$ {\theta _{ji}} $ 表示坐标系$ \{ {{O_{j\left( {i - 1} \right)}}} \} $ 的x轴与坐标系$ \{ {{O_{ji}}} \} $ 的x轴之间的夹角。第j条机械腿的足端坐标系
$\{ {{O_{j4}}} \}$ 相对于根坐标系$ \{ {{O_{j0}}} \} $ 的变换矩阵为$$ {}_0^4{{\boldsymbol{T}}_j} = {}_0^1{{\boldsymbol{T}}_j}{}_1^2{{\boldsymbol{T}}_j}{}_2^3{{\boldsymbol{T}}_j}{}_3^4{{\boldsymbol{T}}_j} $$ (2) 第j条腿根坐标系
$\{ {{O_{j0}}}\}$ 相对于形心坐标系$\left\{ {{O_B}} \right\}$ 的变换矩阵为$$ {}_B^0{{\boldsymbol{T}}_j} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{j0}}}&{ - \sin {\theta _{j0}}}&0&{{l_{j0}}\cos {\theta _{j0}}} \\ {\sin {\theta _{j0}}}&{\cos {\theta _{j0}}}&0&{{l_{j0}}\sin {\theta _{j0}}} \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] $$ (3) 式中,
${\theta _{j0}}$ 、${l_{j0}}$ 分别为根坐标系相对于形心坐标系的旋转角度、平移距离。足端坐标系
$\{ {{O_{j4}}}\}$ 相对于坐标系$\left\{ {{O_B}} \right\}$ 的位姿为$$ {}_B^4{{\boldsymbol{T}}_j} = {}_B^0{{\boldsymbol{T}}_j}{}_0^4{{\boldsymbol{T}}_j} $$ (4) 足端在坐标系
$\left\{ {{O_B}} \right\}$ 和$ \left\{ {{O_{j0}}} \right\} $ 的坐标满足$$ {}^{j0}{p_{j4}} = {}_{j0}^B{{\boldsymbol{T}}_j}{}^B{p_{j4}} $$ (5) 1.2 逆运动学
运动学逆解是指已知足端在坐标系
$ \{ {{O_{j0}}}\} $ 下的坐标, 求期望的关节角度$ {\theta }_{j1}、{\theta }_{j2}、{\theta }_{j3} $ 。利用机械腿关节位置的几何关系, 可得$$ {\theta _{j1}} = \arctan \frac{{{}^{j0}{y_{j4}}}}{{{}^{j0}{x_{j4}}}} $$ (6) $$ {\theta _{j3}} = {\text{π }} - k $$ (7) $$ \theta_{j2}=\arctan2(k_1k_2-k_3k_4,k_1k_4+k_2k_3) $$ (8) 式中:
$$ k=\arccos\left( \frac{l_{j2}^2+l_{j3}^2-\left(\sqrt{^{j0}x_{j4}^2+^{j0}y_{j4}^2}-l_{j1}\right)^2-^{j0}{\textit{z}}_{j4}^2}{2l_{j2}l_{j3}} \right)\text{; } $$ $ k_1=\; ^{j0} \textit{z}_{j4} $ ;$ k_2=l_{j3}\cos\theta_{j3}+l_{j2} $ ;$ k_3=\;^{j0} x_{j4}\cos\theta_{j1}+ ^{j0}y_{j4}\sin\theta_{j1}-l_{j1} $ ;$ k_4=-l_{j3}\sin\theta_{j3} $ 。2. 水下六足机器人足端轨迹优化
水下六足机器人的运动是通过支撑腿和摆动腿实现的。合理规划支撑腿和摆动腿的轨迹以及切换规则, 即可实现水下六足机器人的行走。
2.1 支撑腿足端轨迹规划
机械腿处于支撑状态时, 足端相对地面没有移动, 也就是足端相对于世界坐标系
$\left\{ {{O_G}} \right\}$ 没有移动。因此, 只需对身体相对于世界坐标系$\left\{ {{O_G}} \right\}$ 的轨迹进行五次多项式优化, 即可求解出足端相对于身体的平滑轨迹, 进而可以求解出支撑腿的期望关节角度。2.2 摆动腿足端轨迹规划
考虑到海底地形崎岖不平, 水下六足机器人足端采用矩形轨迹。由于水动力的影响, 腿在摆动过程中会受到较大的水阻力, 而水阻力主要是由刚体的速度和加速度造成的。摆动腿的速度和加速度是由关节角轨迹决定的, 因此, 需要对足端轨迹进行优化, 确保逆运动学求解出的期望关节角轨迹足够平滑, 以便关节电机能够实现对期望关节角轨迹的跟踪。采用五次多项式对足端轨迹进行优化, 并对起始点和终止点处的位置、速度及加速度进行约束。优化后的足端轨迹为
$$ x\left(t\right)=\left\{\begin{array}{*{20}{l}}0,\; t\leqslant\dfrac{T}{3} \\ Q\left(t-\dfrac{T}{3},\dfrac{T}{3},0,x_d,0,0\right),\; \dfrac{T}{3} < t < \dfrac{2T}{3} \\ 0,\; \dfrac{2T}{3}\leqslant t\leqslant T\end{array}\right. $$ (9) $$ y\left(t\right)=\left\{\begin{array}{*{20}{l}}0,\; t\leqslant\dfrac{T}{3} \\ Q\left(t-\dfrac{T}{3},\dfrac{T}{3},0,y_d,0,0\right),\; \dfrac{T}{3} < t < \dfrac{2T}{3} \\ 0,\; \dfrac{2T}{3}\leqslant t\leqslant T\end{array}\right. $$ (10) $$ {\textit{z}}(t)=\left\{\begin{array}{*{20}{l}}Q\left(t,\dfrac{T}{3},0,h_d,0,0\right),\; t\leqslant\dfrac{T}{3} \\ h_d,\; \dfrac{T}{3} < t < \dfrac{2T}{3} \\ Q\left(t-\dfrac{2T}{3},\dfrac{T}{3},h_d,0,0,0\right),\; \dfrac{2T}{3}\leqslant t\leqslant T\end{array}\right. $$ (11) 式中:
$ Q\left(\cdot\right) $ 为五次多项式拟合函数, 输入按顺序为时间—周期—起始位置—终止位置—起始速度—终止速度—起始加速度—终止加速度, 缺省状态下加速度默认为0; t为时间; T为轨迹周期;$ x_d $ 为纵向步幅;$ y_d $ 为纵向步幅;${h_d}$ 为最大抬腿高度。$ {x}_{d}、{y}_{d}、{h}_{d}、T $ 分别取0.5、0.2、0.2、2时, 优化后的矩形轨迹如图3所示。3. 水下六足机器人控制系统设计
3.1 总体框架
水下六足机器人控制系统总体框架如图4所示。控制系统接收上位机指令和电机状态反馈量实时规划出符合要求的摆动腿足端矩形轨迹, 并通过五次多项式进行优化; 根据逆运动学求解出期望的关节角, 通过EtherCAT同时发送给18个关节执行模块; 关节电机内部的PID控制器对接收到的期望关节角进行跟踪; 关节执行模块完成关节角的实时跟踪, 身体即可按照规划好的轨迹运动。
图 4 水下机器人控制系统总体框图Figure 4. Overall block diagram of control system of the underwater robot关节执行模块采用无框力矩电机, 内置谐波减速器和双编码器, 有较大的力矩输出, 能满足高精度控制的需求, 并且可以将电机状态反馈给控制系统。
主控采用PC104开发板, 可搭载Ubutun 22.04系统和ROS2系统, 板载以太网接口可用于Ether CAT通信接口, 与关节电机进行通信, 完成指令发送和电机状态接收。
3.2 软件设计
在ROS2环境下设计水下六足机器人控制系统, 将控制系统按功能进行拆分, 设计成ROS2节点。水下六足机器人控制系统主要包含2个重要的ROS2节点, 分别为电机控制节点和机器人控制节点。机器人控制节点和电机控制节点之间使用服务通信, 保证通信的实时性。
3.2.1 电机控制节点
电机控制节点分为电机和ROS2节点2类。电机类用来存放电机信息, ROS2节点类主要包含定时函数和通信反馈函数。定时函数执行流程图如图5所示。
图 5 电机控制节点定时通信流程图Figure 5. Flow chart of the timing communication of the motor control node3.2.2 机器人控制节点
机器人控制节点根据上位机命令和电机反馈信息, 求解出关节执行模块所需的期望关节角度, 并发给电机控制节点。该节点包含的相关变量和函数如表2和表3所示。
表 2 机器人控制节点相关变量Table 2. Related variables contained in robot control node变量名 含义 origin_thigh_trans[6,4] 0号关节在基座下的位置 joint_length[3] $ {l}_{j1}、{l}_{j2}、{l}_{j3} $ theta_stand[6,3] 初始关节角度 theta_now[6,3] 实际关节角度 theta_target[6,3] 期望关节角度 ground_base_coord[3] 机体路径 foot_coordinate_base[6,3] 当前足端位置 foot_coordinate_base_target[6,3] 期望足端位置 speed_target[3] 期望机器人移动速度 step_size[3] 机器最大横纵步幅和
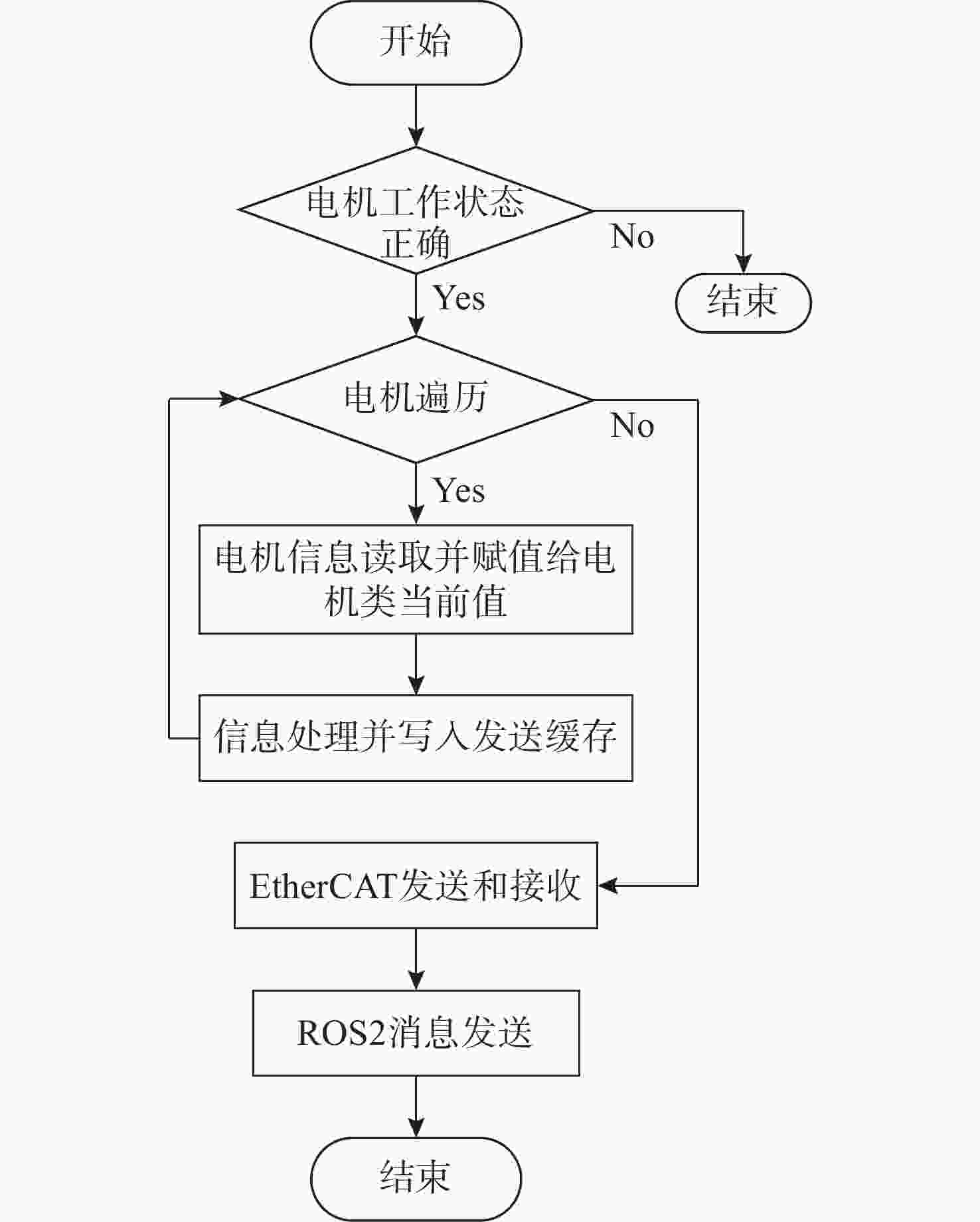
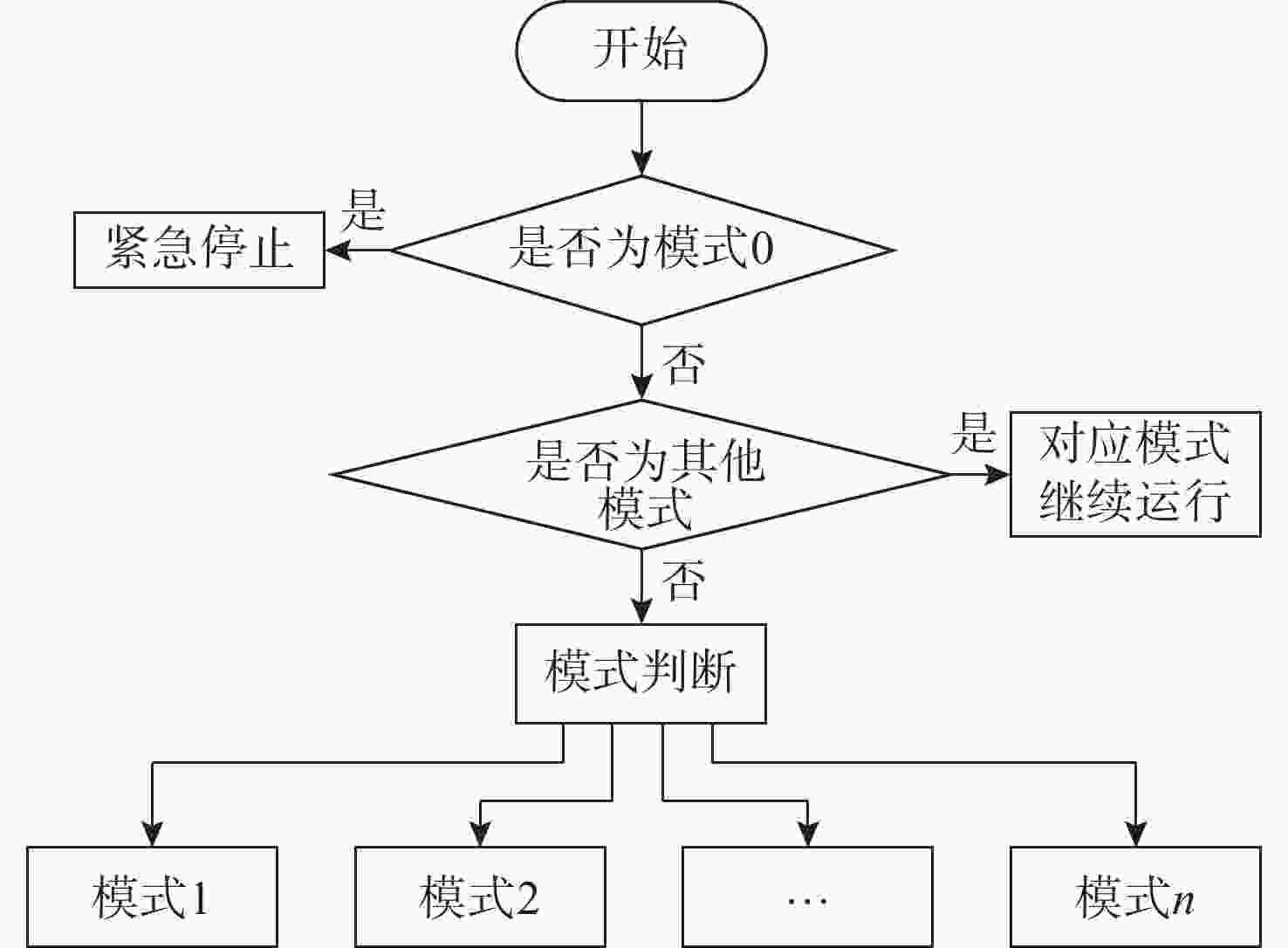
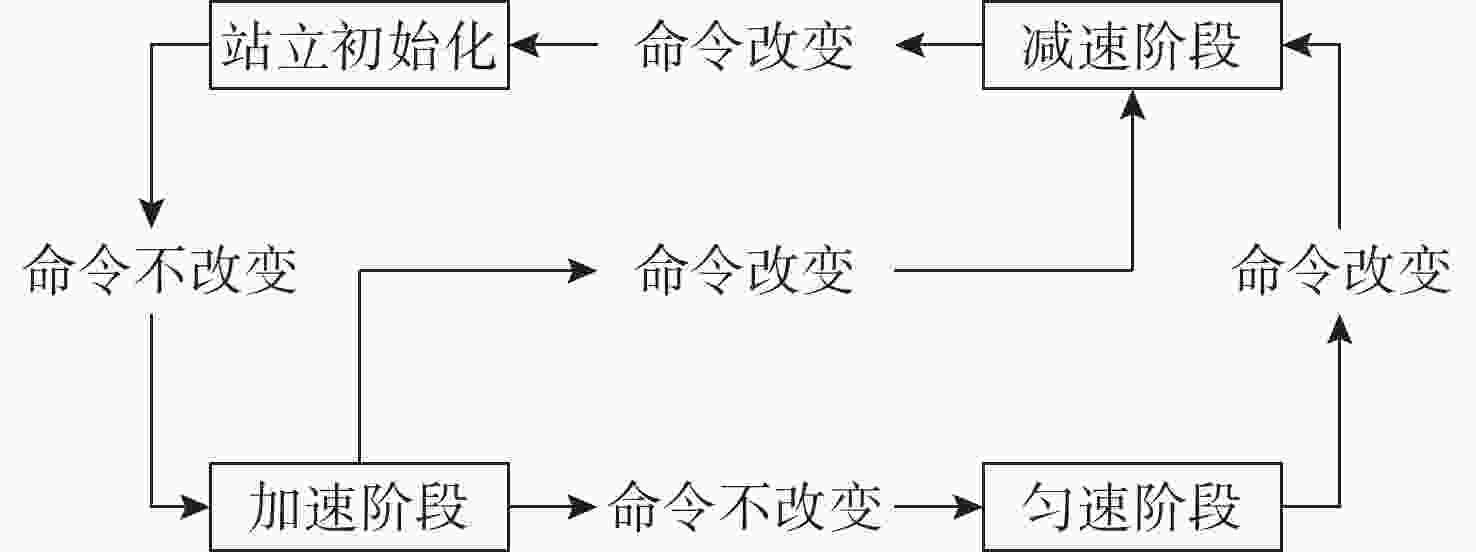
零半径旋转幅度centroid_h 机器人足端离底最大高度 gait_mode 步态模式 robot_mode 工作模式 表 3 机器人控制节点相关函数Table 3. Related functions contained in robot control node函数名 含义 Init() 变量初始化 T_joint_state_init() 正运动学计算 Inverse_Kinematics() 逆运动学计算 Point_to_point_arc() 空间点到点轨迹生成 Foot_track_ground() 摆动腿足端轨迹生成 Stand_init() 站立初始化 Walk_init() 移动速度加速行走 Walk() 移动速度匀速行走 Walk_end() 移动速度减速行走 Period_cal() 状态转换周期计算 Walking_pattern_3() 三角步态工作模式 Walking_pattern_5() 五足步态工作模式 Robot_walk_mode_swap() 移动控制指令是否改变 Robot_interface() 类接口函数 机器人控制节点接口函数负责完成工作模式的识别, 工作流程如图6所示。模式0为机器人紧急停止命令, 有最高的优先级。
图 6 机器人控制节点接口函数工作流程Figure 6. Flow chart of the interface function of robot control node机器人状态切换如图7所示。站立初始化使机器人姿态恢复到初始站立姿态, 加速阶段使速度平滑过度到期望速度, 减速阶段使速度平滑减少到0。
4. 实验验证
为了验证水下六足机器人控制系统的可行性, 在上海交通大学水下工程研究所进行了水池实验, 主要验证了水下六足机器人的2种典型运动模式: 直线行走和原地转动。水下六足机器人携带惯性测量单元(inertial measurement unit, IMU)和多普勒计程仪(Doppler velocity log, DVL)测量艏向角和行走速度。
4.1 直线行走实验
水下六足机器人直线行走实验如图8所示。图9为水下六足机器人从点(−0.804 3, 1.331 8)运动到点(2.201 9, 3.356 3)的轨迹, 移动距离4.251 4 m, 平均速度为0.12 m/s。
图10和图11为2号腿和5号腿关节角跟踪结果, 由于对足端轨迹进行了优化, 期望关节角曲线比较平滑, 关节电机可以跟踪上期望关节角轨迹, 因此, 期望关节角曲线和关节电机反馈的实际关节角曲线基本重合。
图 10 直行实验中2号腿关节角跟踪曲线Figure 10. The joint angle tracking curves of leg 2 in straight walking test
图 11 直行实验中5号腿关节角跟踪曲线Figure 11. The joint angle tracking curves of leg 5 in straight walking test图12和图13为关节电机反馈的扭矩曲线。关节电机输出的最大扭矩为242 Nm, 经过足端轨迹的优化, 期望关节角相对平滑, 角加速度控制在合理范围内, 整个运动过程关节电机扭矩都没有超过最大值。
4.2 转动实验
水下六足机器人转动过程与直线行走相似, 将转动角度划分为若干个区间, 每个区间进行五次多项式优化。在转动实验中, 水下六足机器人身体的艏向角从22.95°逐渐过渡到230.79°, 如图14所示。
图15和图16为2号腿和5号腿的关节跟踪曲线。从关节角跟踪曲线可以看出, 关节电机可以跟踪上期望关节角度。
图 15 转动实验中2号腿关节角跟踪曲线Figure 15. The joint angle tracking curves of leg 2 in turning experiment
图 16 转动实验中5号腿关节角跟踪曲线Figure 16. The joint angle tracking curve of leg 5 in turning experiment图17和图18为关节电机反馈的关节扭矩。由图可知, 关节扭矩没有超过关节电机的最大扭矩, 关节电机在安全状态下运行。
5. 结束语
水下六足机器人能够在海流冲击、崎岖不平的海底进行近地观测和取样。文中采用EtherCAT实现了对水下六足机器人18个关节电机的实时、同步控制; 通过正、逆运动学和足端轨迹规划, 反解出平滑的期望关节角轨迹; 最终在满足关节电机负载要求的情况下, 实现了期望关节角的精确跟踪, 进而实现了水下六足机器人的典型运动模式: 直线行走和转动。
-
图 4 水下机器人控制系统总体框图
Figure 4. Overall block diagram of control system of the underwater robot
图 5 电机控制节点定时通信流程图
Figure 5. Flow chart of the timing communication of the motor control node
图 6 机器人控制节点接口函数工作流程
Figure 6. Flow chart of the interface function of robot control node
图 10 直行实验中2号腿关节角跟踪曲线
Figure 10. The joint angle tracking curves of leg 2 in straight walking test
图 11 直行实验中5号腿关节角跟踪曲线
Figure 11. The joint angle tracking curves of leg 5 in straight walking test
图 15 转动实验中2号腿关节角跟踪曲线
Figure 15. The joint angle tracking curves of leg 2 in turning experiment
图 16 转动实验中5号腿关节角跟踪曲线
Figure 16. The joint angle tracking curve of leg 5 in turning experiment
表 1 机械腿D-H参数表
Table 1. D-H parameters of mechanical leg
i ${a_{j\left( {i - 1} \right)}}/{\text{m}}$ ${\alpha _{j\left( {i - 1} \right)}}/({\text{°}})$ ${d_{ji}}/{\text{m}}$ ${\theta _{ji}}/({\text{°}} )$ 0 ${l_{j{\text{0}}}}$ 0 0 ${\theta _{j{\text{0}}}}$ 1 0 0 0 ${\theta _{j1}}$ 2 ${l_{j1}}$ $90$ 0 ${\theta _{j2}}$ 3 ${l_{j2}}$ 0 0 ${\theta _{j3}}$ 4 ${l_{j3}}$ 0 0 0 
下载: 导出CSV
表 2 机器人控制节点相关变量
Table 2. Related variables contained in robot control node
变量名 含义 origin_thigh_trans[6,4] 0号关节在基座下的位置 joint_length[3] $ {l}_{j1}、{l}_{j2}、{l}_{j3} $ theta_stand[6,3] 初始关节角度 theta_now[6,3] 实际关节角度 theta_target[6,3] 期望关节角度 ground_base_coord[3] 机体路径 foot_coordinate_base[6,3] 当前足端位置 foot_coordinate_base_target[6,3] 期望足端位置 speed_target[3] 期望机器人移动速度 step_size[3] 机器最大横纵步幅和
零半径旋转幅度centroid_h 机器人足端离底最大高度 gait_mode 步态模式 robot_mode 工作模式
下载: 导出CSV
表 3 机器人控制节点相关函数
Table 3. Related functions contained in robot control node
函数名 含义 Init() 变量初始化 T_joint_state_init() 正运动学计算 Inverse_Kinematics() 逆运动学计算 Point_to_point_arc() 空间点到点轨迹生成 Foot_track_ground() 摆动腿足端轨迹生成 Stand_init() 站立初始化 Walk_init() 移动速度加速行走 Walk() 移动速度匀速行走 Walk_end() 移动速度减速行走 Period_cal() 状态转换周期计算 Walking_pattern_3() 三角步态工作模式 Walking_pattern_5() 五足步态工作模式 Robot_walk_mode_swap() 移动控制指令是否改变 Robot_interface() 类接口函数
下载: 导出CSV
-
[1] ZHU X, SONG B, ZHANG D, et al. Analysis of landing strategies and influencing factors of an autonomous underwater vehicle[J]. Ocean Engineering, 2021, 237: 1-10. [2] KATZSCHMANN R K, DELPRETO J, MACCURDY R, et al. Exploration of underwater life with an acoustically controlled soft robotic fish[J]. Science Robotics, 2018, 3(16): 1-27. [3] PICARDI G, CHELLAPURATH M, IACOPONI S, et al. Bioinspired underwater legged robot for seabed exploration with low environmental disturbance[J]. Science Robotics, 2020, 5(42): 1-14. [4] SHIM H, YOO S Y, KANG H, et al. Development of arm and leg for seabed walking robot CRABSTER200[J]. Ocean Engineering, 2016, 116: 55-67. doi: 10.1016/j.oceaneng.2016.02.028 [5] WANG L, LU Y, ZHANG Y, et al. Design and soft-landing control of underwater legged robot for active buffer landing on seabed[J]. Ocean Engineering, 2022, 266(24): 1-16. [6] 陈铭, 冷静. 深海大型爬行机器人研究现状[J]. 海洋工程, 2020, 38: 156-168.CHEN M, LENG J. The development of deep-sea large-scale crawling robots[J]. Ocean Engineering, 2020, 38: 156-168. [7] 陈虹, 王心亮, 魏伟, 等. 深海爬游机器人概念及关键技术分析[J]. 中国舰船研究, 2018, 13(6): 19-26.CHEN H, WANG X L, WEI W, et al. Concept and key technology analysis of deep-sea walking-swimming robot[J]. Chinese Journal of Ship Research, 2018, 13(6): 19-26. [8] CHEN T, LI Y, RONG X, et al. Design and control of a novel leg-arm multiplexing mobile operational hexapod robot[J]. IEEE Robotics and Automation Letters, 2022, 7(1): 382-389. doi: 10.1109/LRA.2021.3127639 [9] BAL C. Neural coupled central pattern generator based smooth gait transition of a biomimetic hexapod robot[J]. Neurocomputing, 2021, 420: 210-226. doi: 10.1016/j.neucom.2020.07.114 [10] YU H, GAO H, DENG Z. Enhancing adaptability with local reactive behaviors for hexapod walking robot via sensory feedback integrated central pattern generator[J]. Robotics and Autonomous Systems, 2020, 124: 1-17. [11] CHEN C, ZHA F, GUO W, et al. Trajectory adaptation of biomimetic equilibrium point for stable locomotion of a large-size hexapod robot[J]. Autonomous Robots, 2020, 45(1): 155-174. [12] 王心亮, 肖前进, 马哲松, 等. 水下爬游机器人足端运动空间分析[J]. 中国造船, 2019, 60(增刊1): 444-451. doi: 10.3969/j.issn.1000-4882.2019.z1.062 [13] DAVLIAKOS I, RODITIS I, LIKA K, et al. Design, development, and control of a tough electrohydraulic hexapod robot for subsea operations[J]. Advanced Robotics, 2018, 32(9): 477-499. doi: 10.1080/01691864.2018.1461684 -
下载:
点击查看大图
计量
- 文章访问数: 148
- HTML全文浏览量: 51
- PDF下载量: 43
- 被引次数: 0
