Underwater Positioning Method Based on Vision-Inertia-Pressure Fusion
-
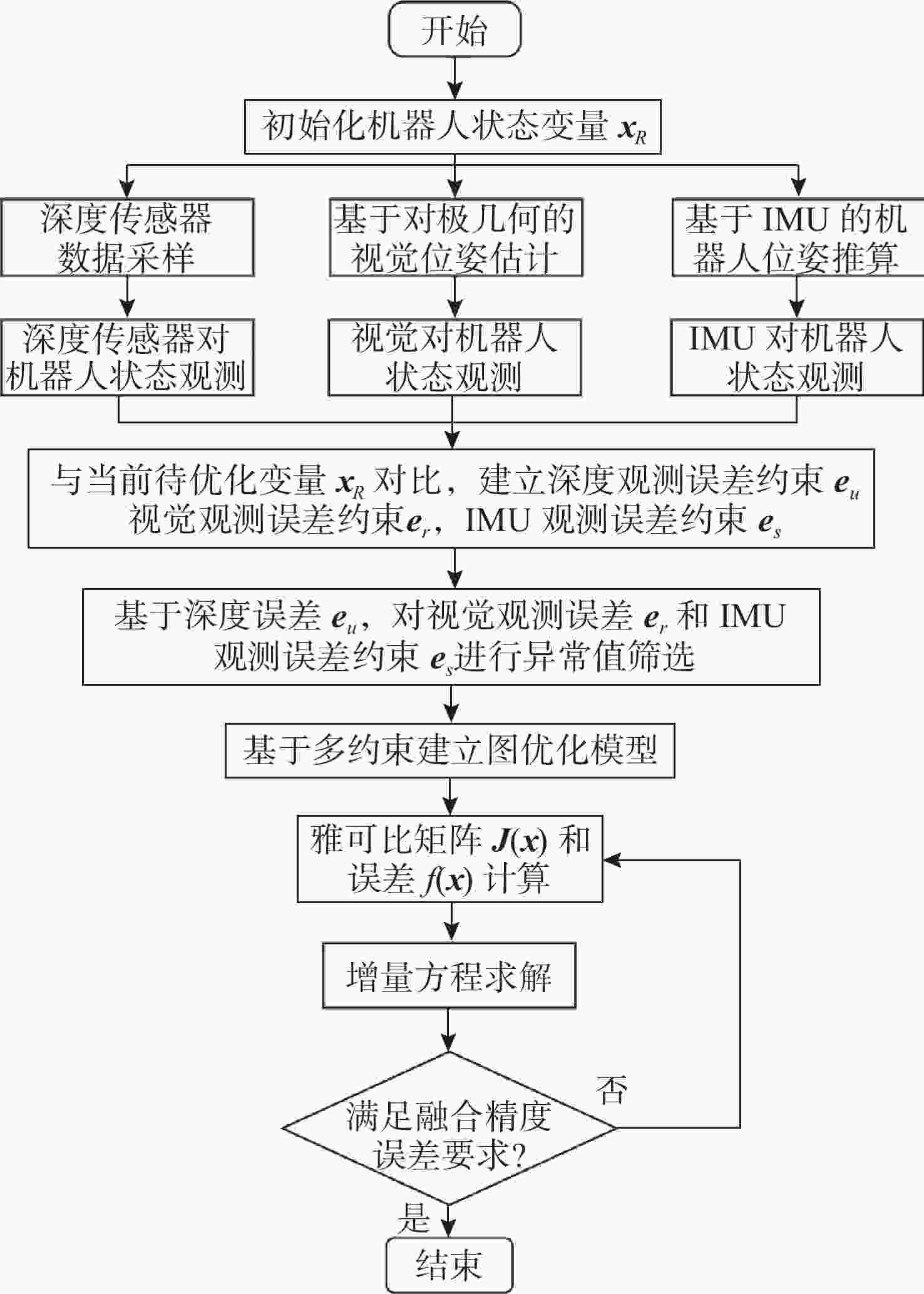
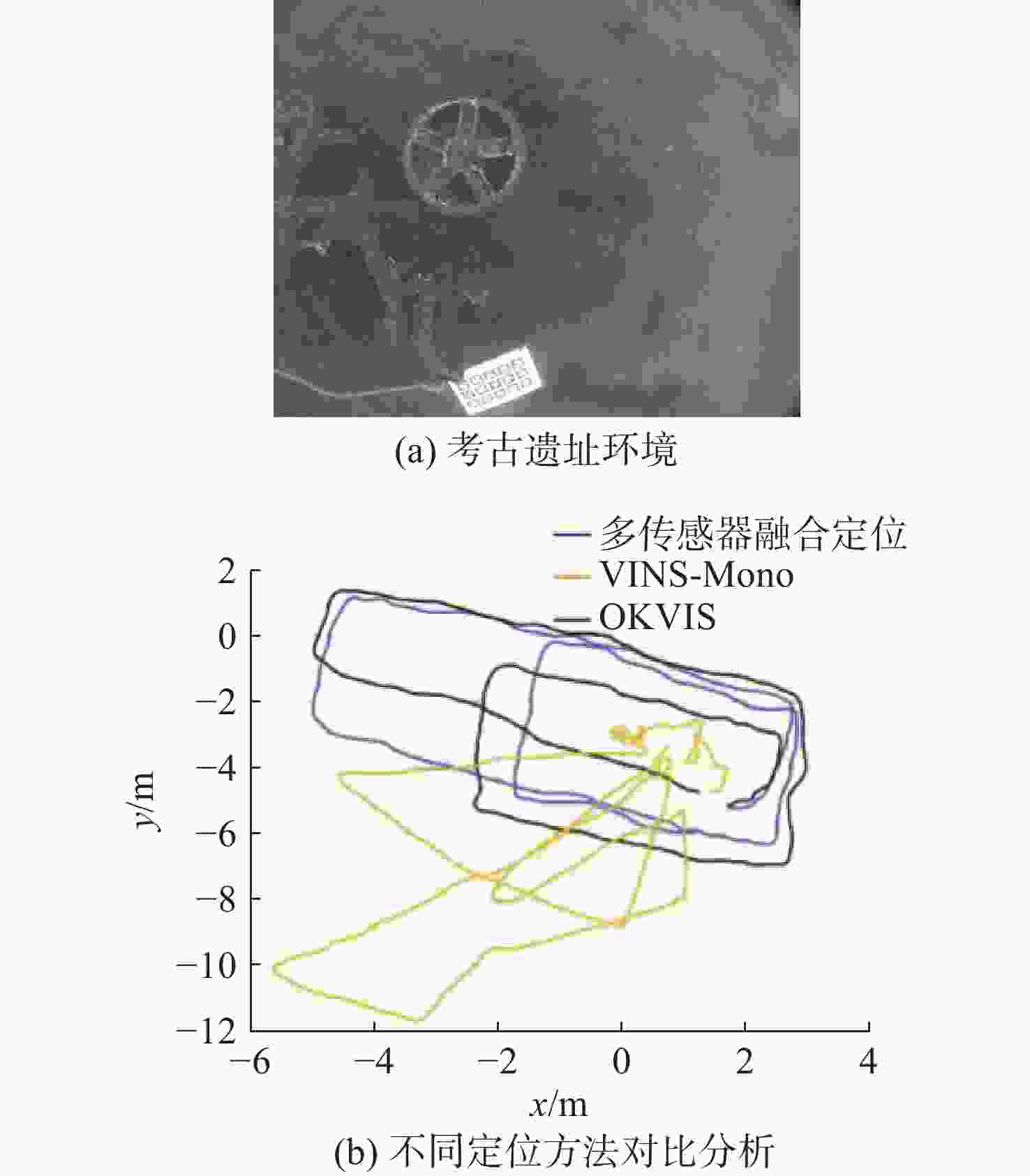
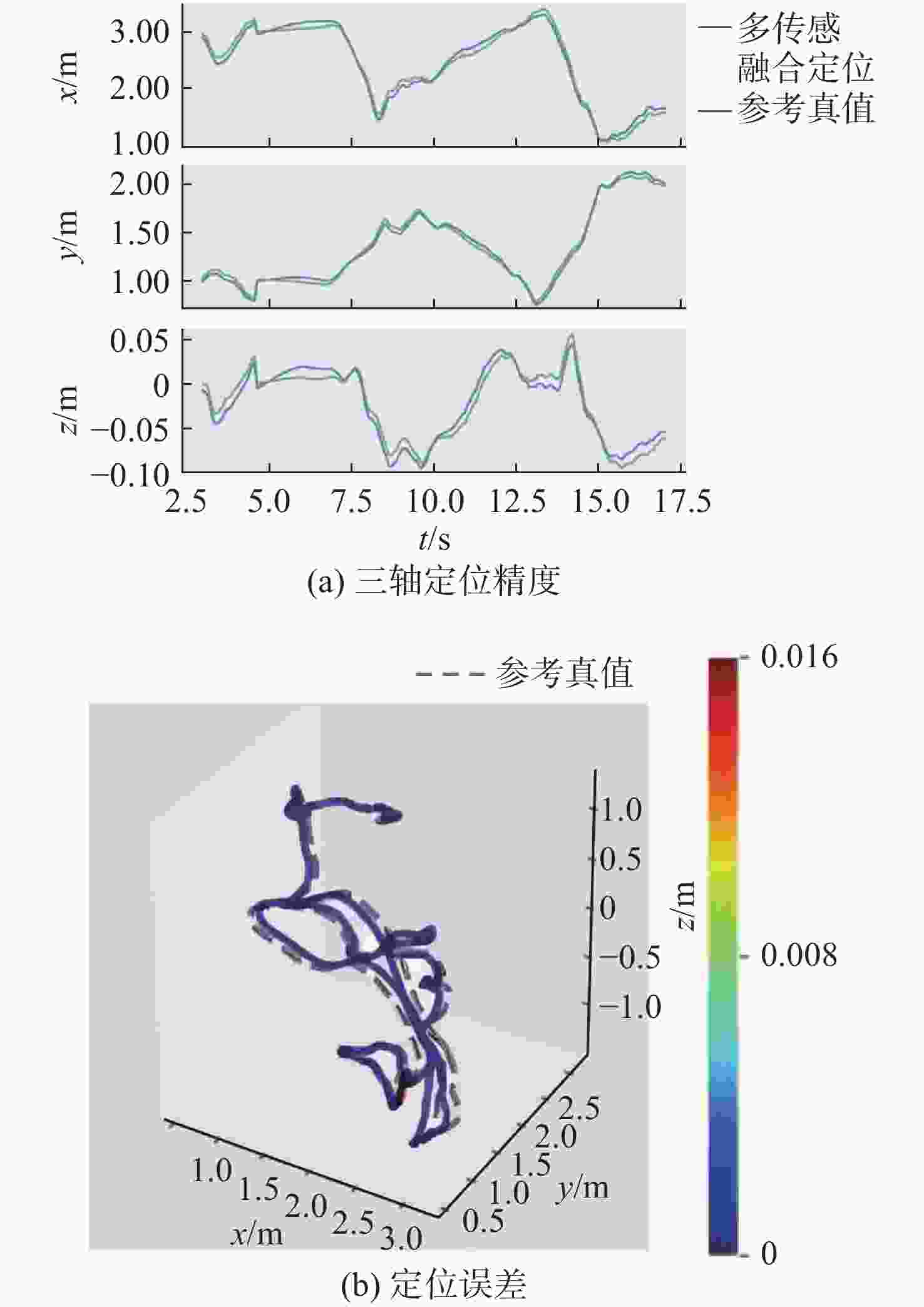
摘要: 水下机器人在水下非结构化环境作业时, 难以依赖外部基站进行定位, 多传感器融合自主定位在此类环境具有重要应用价值。文中针对水下多传感器融合定位中视觉定位稳定性差、惯性导航存在较大漂移等问题, 提出一种紧组合视觉、惯性及压力传感器的多传感器融合定位方法。通过图优化方法进行多传感器融合, 基于深度信息对视觉惯性数据进行误差辨识以提升融合数据质量; 针对融合定位过程中出现的漂移和定位丢失问题, 采用深度传感器进行权重分配以提供更加细致的系统初始化, 同时引入闭环检测和重定位方法, 有效改善漂移和定位丢失的问题。通过试验验证发现, 所提出的融合定位算法相较于视觉惯性融合定位方法精度提升48.4%, 具有更好的精度和鲁棒性, 实际工况定位精度可达厘米级。Abstract: In underwater unstructured environments, robots face difficulties in relying on external base stations for localization. Therefore, autonomous localization using multi-sensor fusion has significant application value in such settings. This paper aimed to address issues such as poor stability in visual localization and substantial drift in inertial navigation within underwater multi-sensor fusion localization and proposed a tightly integrated multi-sensor fusion localization method that combined visual, inertial, and pressure sensors. By utilizing graph optimization techniques for multi-sensor fusion and identifying errors in visual-inertial data based on depth information, the quality of the fused data was enhanced. To address drift and localization loss during the fusion localization process, a depth sensor was employed for weight allocation to provide more detailed system initialization. Additionally, closed-loop detection and relocalization methods were introduced to effectively mitigate drift and localization loss. Experimental validation demonstrates that the proposed fusion localization algorithm improves accuracy by 48.4% compared to visual-inertial fusion localization methods, achieving superior precision and robustness. The actual positioning accuracy can reach the centimetre level.
-
图 5 考古遗址中不同定位方法定位精度对比
Figure 5. Comparison of positioning accuracy among different positioning methods in archaeological sites
图 6 水下沉船环境下不同定位方法定位精度对比
Figure 6. Comparison of positioning accuracy among different positioning methods in underwater shipwreck environments
图 8 无重定位和回环检测模块下定位精度
Figure 8. Positioning accuracy without relocation and loopback detection module
表 1 传感器参数表
Table 1. Sensor parameters
相机 型号 ZED2 分辨率 3 840×1 080 帧率/(帧/s) 30 视场角/(°) 94.5 IMU 型号 MEMS-MPU-9250 陀螺仪频率/Hz 200 加速度计频率/Hz 200 磁力计频率/Hz 200 
下载: 导出CSV
表 2 融合算法精度测试结果
Table 2. Results of fusion algorithm accuracy test
运动形式 最大误差/m 直航 0.064 转向 0.028 快速机动 0.127
下载: 导出CSV
-
[1] WANG Y, MA X, WANG J, et al. Pseudo-3D vision-inertia based underwater self-localization for AUVs[J]. IEEE Transactions on Vehicular Technology, 2020, 69(7): 7895-7907. doi: 10.1109/TVT.2020.2993715 [2] SMITHANIK J R, ATKINS E M, SANNER R M. Visual positioning system for an underwater space simulation environment[J]. Journal of Guidance, Control, and Dynamics, 2016, 29(4): 858-869. [3] CHENG C, WANG C, YANG D, et al. Underwater localization and mapping based on multi-beam forward looking sonar[J]. Frontiers in Neurorobotics, 2022, 15: 801956. doi: 10.3389/fnbot.2021.801956 [4] SHEN Y, ZHAO C, LIU Y, et al. Underwater optical imaging: Key technologies and applications review[J]. IEEE Access, 2021, 9: 85500-85514. doi: 10.1109/ACCESS.2021.3086820 [5] RAVEENDRAN S, PATIL M D, BIRAJDAR G K. Underwater image enhancement: A comprehensive review, recent trends, challenges and applications[J]. Artificial Intelligence Review, 2021, 54: 5413-5467. doi: 10.1007/s10462-021-10025-z [6] LI C, GUO C, REN W, et al. An underwater image enhancement benchmark dataset and beyond[J]. IEEE Transactions on Image Processing, 2019, 29: 4376-4389. [7] SHAUKAT N, LI A Q, REKLEITIS I. Svin2: An underwater slam system using sonar, visual, inertial, and depth sensor[C]//2019 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS). Macau: IEEE, 2019: 1861-1868. [8] WANG X, FAN X, SHI P, et al. An overview of key SLAM technologies for underwater scenes[J]. Remote Sensing, 2023, 15(10): 2496. doi: 10.3390/rs15102496 [9] HU K, WANG T, SHEN C, et al. Overview of underwater 3D reconstruction technology based on optical images[J]. Journal of Marine Science and Engineering, 2023, 11(5): 949. doi: 10.3390/jmse11050949 [10] LEUTENEGGER S, FURGALE P, RABAUD V, et al. Keyframe-based visual-inertial slam using nonlinear optimization[J]. Proceedings of Robotis Science and Systems, 2023, 51: 5213-5667. [11] QIN T, LI P, SHEN S. VINS-MOMO: A robust and versatile monocular visual-inertial state estimator[J]. IEEE Transactions on Robotics, 2018, 34(4): 1004-1020. doi: 10.1109/TRO.2018.2853729 [12] MOURIKIS A I, ROUMELIOTIS S I. A multi-state constraint Kalman filter for vision-aided inertial navigation[C]//Proceedings 2007 IEEE International Conference on Robotics and Automation. Roma, Italy: IEEE, 2017. [13] SIBLEY G, MATTHIES L, SUKHATME G. Sliding window filter with application to planetary landing[J]. J. Field Robot, 2019, 27(5): 587-608. [14] 王霞, 左一凡. 视觉SLAM研究进展[J]. 智能系统学报, 2020, 15(5): 825-834. doi: 10.11992/tis.202004023WANG X, ZUO Y F. Advances in visual SLAM research[J]. CAAI Transactions on Intelligent Systems, 2020, 15(5): 825-834. doi: 10.11992/tis.202004023 [15] MEI C, RIVES P. Single view point omnidirectional camera calibration from planar grids[C]//Proceedings 2007 IEEE International Conference on Robotics and Automation. Roma, Italy: IEEE, 2007. [16] FERRERA M, CREUZE V, MORAS J, et al. AQUALOC: An underwater dataset for visual-inertial-pressure localization[J]. The International Journal of Robotics Research, 2019, 38(14): 1549-1559. doi: 10.1177/0278364919883346 [17] LIN Y, GAO F, QIN T, et al. Autonomous aerial navigation using monocular visual inertial fusion[J]. Journal of Field Robot, 2017, 35: 23-51. [18] JIANG H, WANG W, SHEN Y, et al. Efficient planar pose estimation via UWB measurements[C]//2023 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2023: 1954-1960. -
点击查看大图
图(11) / 表(2)
计量
- 文章访问数: 153
- HTML全文浏览量: 54
- PDF下载量: 40
- 被引次数: 0
