Adaptive Neural Network Control of ROV under Ocean Current Disturbance
-
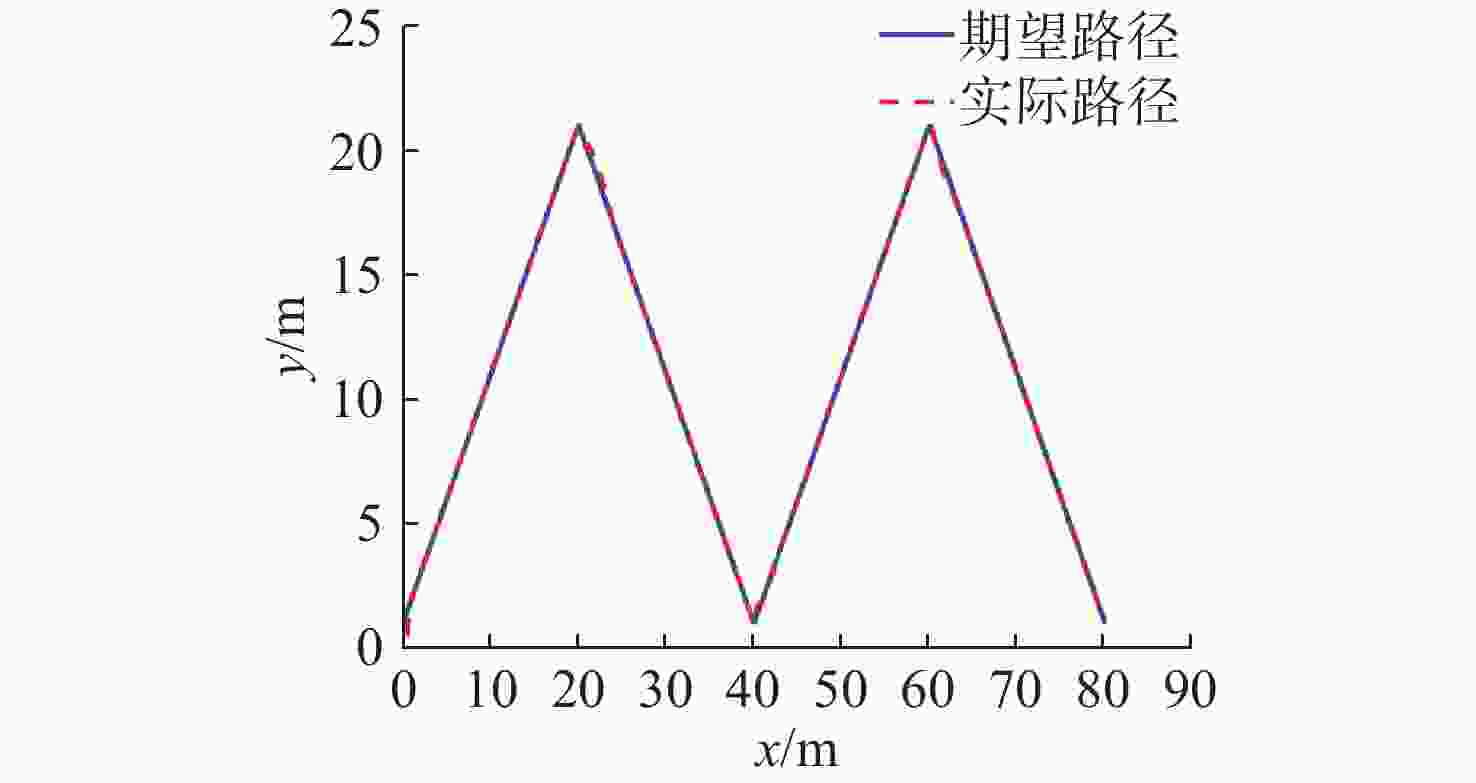
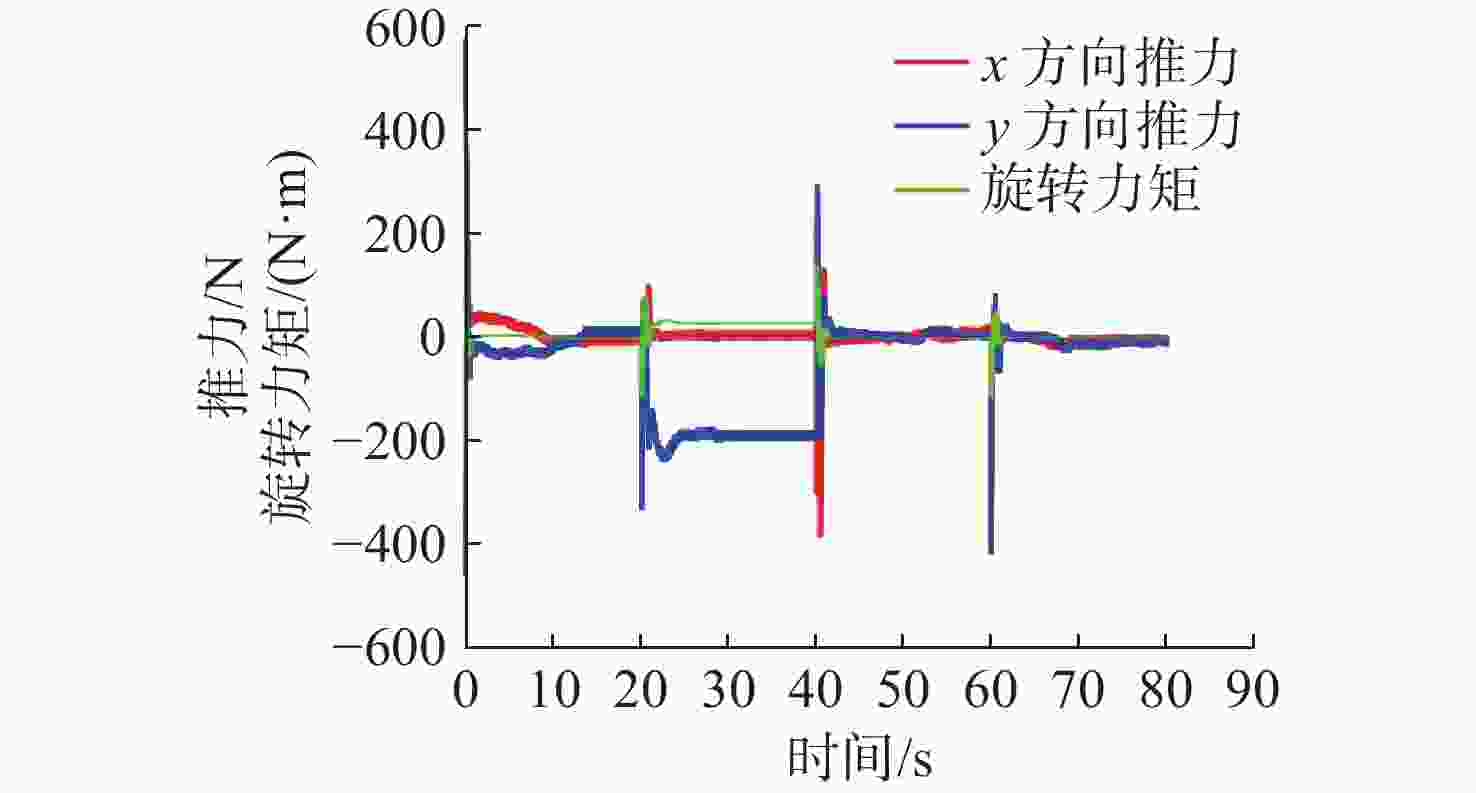
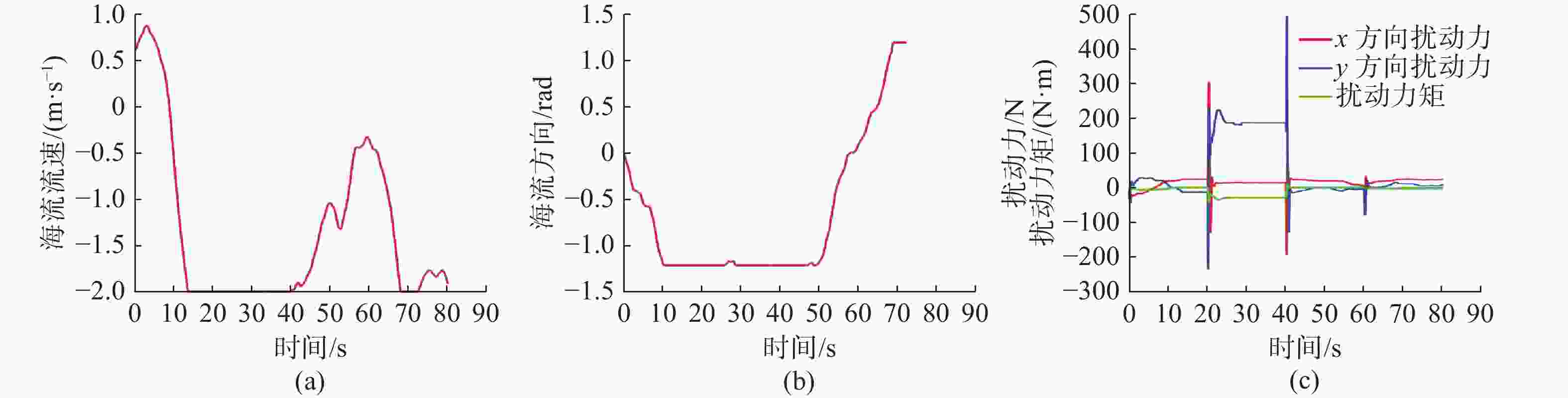
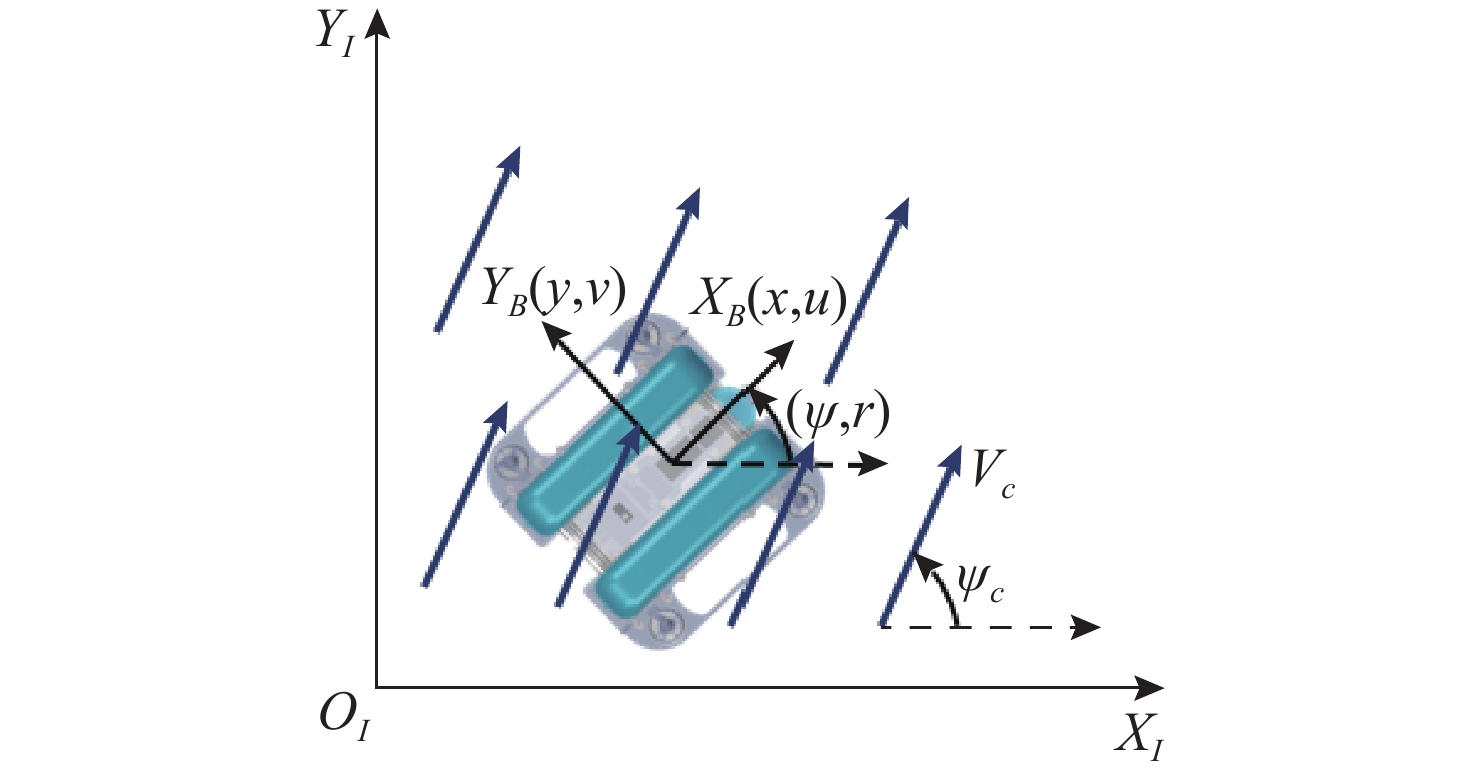
摘要: 针对水下遥控机器人(ROV)在模型参数不确定和海流扰动下的运动控制问题, 基于有限时间命令滤波和径向基(RBF)神经网络设计出一种自适应反步控制系统。首先, 基于马尔科夫过程构建随机海流模型, 并构建海流扰动下的ROV数学模型; 其次, 针对期望速度引入命令滤波技术, 以减少传统反步法迭代导数带来的计算量; 再次, 利用径向基神经网络对ROV模型的不确定项和外部未知扰动进行估计, 并设计自适应神经网络控制器; 最后, 利用李雅普诺夫稳定性理论证明了闭环控制系统的稳定性。仿真结果表明, 本文设计的控制器可以实现ROV航行的精确控制,并能够有效抑制模型的不确定项和海流扰动对ROV运动的影响。Abstract: Aiming at the motion control problem of remotely operated unmanned vehicles (ROV) under uncertain model parameters and ocean current disturbance, an adaptive back-stepping control system is designed based on the limited time command filter and feedback base Radial Basis Function (RBF) neural network. Firstly, construct a stochastic ocean current model based on the Markov process, and construct a ROV mathematical model of velocity under ocean current disturbance; secondly, introduce command filtering technology for the desired speed to reduce the amount of calculation caused by the iterative derivative of the traditional back-stepping method; thirdly, use radial basis neural network to estimate the uncertainty terms and external unknown disturbances of the ROV model, and design an adaptive neural network controller; finally, Lyapunov stability theory is used to prove the stability of the closed-loop control system. The simulation results show that the controller designed in this paper can achieve precise control of ROV navigation, and can realize the uncertainty term of the effective stagnation model and the impact of sea current disturbance on ROV motion.
-
图 3 海流扰动下ROV实际路径和期望路径
Figure 3. Actual path and desired path of ROV under ocean current disturbance
表 1 控制系统性能量化分析
Table 1. Quantitative analysis of control system performance
性能参数 ${E_{MAX}}$ ${M_{MAE}}$ ${R_{RMSE}}$ $x/m$ 0.0 049 0.0 186 0.0 569 $y/m$ 0.0 032 0.0 150 0.0 506 $\psi /rad$ 0.0 001 0.0 223 0.1 416 
下载: 导出CSV
表 2 RBF神经网络性能量化分析
Table 2. Quantitative analysis of RBF neural network performance
性能参数 ${E_{MAX}}$ ${M_{MAE}}$ ${R_{RMSE}}$ $ {\hat f_1} $ 0.0 717 0.1 034 0.4 411 $ {\hat f_2} $ 0.1 321 0.3 843 1.2 340 $ {\hat f_3} $ 0.0 395 0.2 476 1.0 525
下载: 导出CSV
-
[1] 赵大刚, 张顺, 高适, 等. 海流对水下航行器运动及载荷影响研究综述[J]. 中国舰船研究, 2024, 19(5): 1-16.ZHAO D G, ZHANG S, GAO S, et al. Review of influence of underwater vehicle motion and load under current[J]. Chinese Journal of Ship Research, 2024, 19(5): 1-16. [2] Panda J P, Mitra A, Warrior H V. A review on the hydrodynamic characteristics of autonomous underwater vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2021, 235(1): 15-29. doi: 10.1177/1475090220936896 [3] 姚绪梁, 王晓伟, 蒋晓刚, 等. 海流干扰下的欠驱动AUV三维路径跟踪控制[J]. 哈尔滨工业大学学报, 2019, 51(3): 37-45. doi: 10.11918/j.issn.0367-6234.201709002YAO X L, WANG X W, JIANG X G, et al. Control for 3D path following of underactuated autonomous underwater vehicle under current disturbance[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 37-45. doi: 10.11918/j.issn.0367-6234.201709002 [4] Huang B, Yang Q. Disturbance observer-based double-loop sliding-mode control for trajectory tracking of work-class ROVs[J]. Journal of Marine Science and Engineering, 2022, 10(5): 601. doi: 10.3390/jmse10050601 [5] Sakiyama J, Motoi N. Position and attitude control method using disturbance observer for station keeping in underwater vehicle[C]//IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society. Washington, DC: IEEE, 2018: 5469-5474. [6] GUERRERO J, TORRES J, CREUZE V, et al. Adaptive disturbance observer for trajectory tracking control of underwater vehicles[J]. Ocean Engineering, 2020, 200(15): 107080. [7] 陈浩华, 赵红, 王宁, 等. 复杂扰动下水下机器人的轨迹精确跟踪控制[J]. 中国舰船研究, 2022, 17(2): 98-108CHEN H H, ZHAO H, WANG N, et al. Accurate track control of unmanned underwater vehicle under complex disturbances[J]. Chinese Journal of Ship Research, 2022, 17(2): 98-108. [8] PATRE B M, LONDHE P S, WAGHMARE L M, et al. Disturbance estimator based non-singular fast fuzzy terminal sliding mode control of an autonomous underwater vehicle[J]. Ocean Engineering, 2018, 159: 372-387. doi: 10.1016/j.oceaneng.2018.03.082 [9] QIU J, MA M, WANG T, et al. Gradient descent-based adaptive learning control for autonomous underwater vehicles with unknown uncertainties[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(12): 5266-5273. doi: 10.1109/TNNLS.2021.3056585 [10] 张帅军, 刘卫东, 李乐, 等. 基于RBF神经网络补偿的ROV运动控制算法[J]. 水下无人系统学报, 2024, 32(2): 311-319. doi: 10.11993/j.issn.2096-3920.2023-0033ZHANG S J, LIU W D, LI L, et al. ROV motion control algorithm based on RBF neural network compensation[J]. Journal of Unmanned Undersea Systems, 2024, 32(2): 311-319. doi: 10.11993/j.issn.2096-3920.2023-0033 [11] LI D, HAN H, QIAO J. Deterministic learning-based adaptive neural control for nonlinear full-state constrained systems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 34(8): 5002-5011. [12] CHU Z, ZHU D, YANG S X. Observer-based adaptive neural network trajectory tracking control for remotely operated vehicle[J]. IEEE Transactions on Neural networks and learning systems, 2016, 28(7): 1633-1645. [13] ANDERLINI E, PARKER G G, THOMAS G. Control of a ROV carrying an object[J]. Ocean Engineering, 2018, 165(1): 307-318. [14] LONG C, QIN X, BIAN Y, et al. Trajectory tracking control of ROVs considering external disturbances and measurement noises using ESKF-based MPC[J]. Ocean Engineering, 2021, 241(1): 109991. [15] GARCÍA-VALDOVINOS L G, FONSECA-NAVARRO F, AIZP- URU-ZINKUNEGI J, et al. Neuro-sliding control for underwater ROV’s subject to unknown disturbances[J]. Sensors, 2019, 19(13): 2943. doi: 10.3390/s19132943 [16] CUI R, YANG C, LI Y, et al. Adaptive neural network control of AUVs with control input nonlinearities using reinforcement learning[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(6): 1019-1029. doi: 10.1109/TSMC.2016.2645699 [17] HUANG B, YANG Q. Disturbance observer-based double-loop sliding-mode control for trajectory tracking of work-class ROVs[J]. Journal of Marine Science and Engineering, 2022, 10(5): 601. doi: 10.3390/jmse10050601 [18] 罗一汉, 吴家鸣, 苏柏铭, 等. 考虑模型偏差和时变扰动的水下机器人轨迹跟踪控制[J]. 舰船科学技术, 2023, 45(24): 108-115. doi: 10.3404/j.issn.1672-7649.2023.24.020LUO Y H, WU J M, SU B M, et al. Trajectory tracking control of underwater vehicle considering model uncertainty and time-varying disturbance[J]. Ship Science and Technology, 2023, 45(24): 108-115. doi: 10.3404/j.issn.1672-7649.2023.24.020 [19] MUÑOZ-VÁZQUEZ A J, RAMÍREZ-RODRÍGUEZ H, PARRA-VEGA V, et al. Fractional sliding mode control of underwater ROVs subject to non-differentiable disturbances[J]. International Journal of Control, Automation and Systems, 2017, 15: 1314-1321. doi: 10.1007/s12555-015-0210-0 [20] CHO G R, LI J H, PARK D, et al. Robust trajectory tracking of autonomous underwater vehicles using back-stepping control and time delay estimation[J]. Ocean Engineering, 2020, 201: 107131. doi: 10.1016/j.oceaneng.2020.107131 [21] 谢争明. 全驱动自主水下机器人回收动力定位控制研究[D]. 江苏: 江苏科技大学, 2021. [22] 刘丽萍, 王红燕. 基于海流观测的欠驱动AUV自适应反演滑模轨迹跟踪[J]. 天津大学学报(自然科学与工程技术版), 2020, 53(7): 745-753.LIU L P, WANG H Y. Adaptive backstepping sliding mode for underactuated auv trajectory tracking based on ocean current observer[J]. Journal of Tianjin University, 2020, 53(7): 745-753. [23] LEVANT A. Higher-order sliding modes, differentiation and output-feedback control[J]. International journal of Control, 2003, 76(9-10): 924-941. doi: 10.1080/0020717031000099029 [24] YU J, SHI P, ZHAO L. Finite-time command filtered backstepping control for a class of nonlinear systems[J]. Automatica, 2018, 92: 173-180. doi: 10.1016/j.automatica.2018.03.033 [25] BUTCHER J C. Numerical methods for ordinary differential equations[M]. John Wiley & Sons, 2016. [26] DAI S L, WANG C, LUO F. Identification and learning control of ocean surface ship using neural networks[J]. IEEE Transactions on Industrial Informatics, 2012, 8(4): 801-810. doi: 10.1109/TII.2012.2205584 -
点击查看大图
图(8) / 表(2)
计量
- 文章访问数: 10
- HTML全文浏览量: 6
- PDF下载量: 1
- 被引次数: 0
