带有输入时延的多无人艇系统固定时间编队控制研究

李健翔; 张文乐; 黎明

doi:10.11993/j.issn.2096-3920.2024-0039

带有输入时延的多无人艇系统固定时间编队控制研究

doi: 10.11993/j.issn.2096-3920.2024-0039

李健翔^1,,
张文乐^{1, 2,},
黎明^{1, 2,}

1.
中国海洋大学工程学院, 山东青岛, 26600; 3
2.
山东省海洋智能装备技术工程研究中心, 山东青岛, 266003

基金项目: 山东省重点研发计划(重大科技创新工程)(2023ZLGX04); 山东省自然科学基金面上项目(ZR2023MF086) 资助.

详细信息

作者简介:
李健翔(1999-), 男, 在读硕士, 主要研究方向为海上多无人艇固定时间协同控制

中图分类号: TP181; TP242.6
计量
- 文章访问数: 13
- HTML全文浏览量: 10
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-01
- 修回日期: 2024-04-12
- 录用日期: 2024-05-11
- 网络出版日期: 2025-01-20

Fixed-Time Formation Control for Multiple Unmanned Surface Vessel Systems with Input Delay

LI Jianxiang^1
,,
ZHANG Wenle^{1, 2
,},
LI Ming^{1, 2
,}

1.
College of Engineering, Ocean University of China, Qingdao 266000, China
2.
Shandong Marine Intelligent Equipment Technology Engineering Research Center, Qingdao 266000, China

摘要

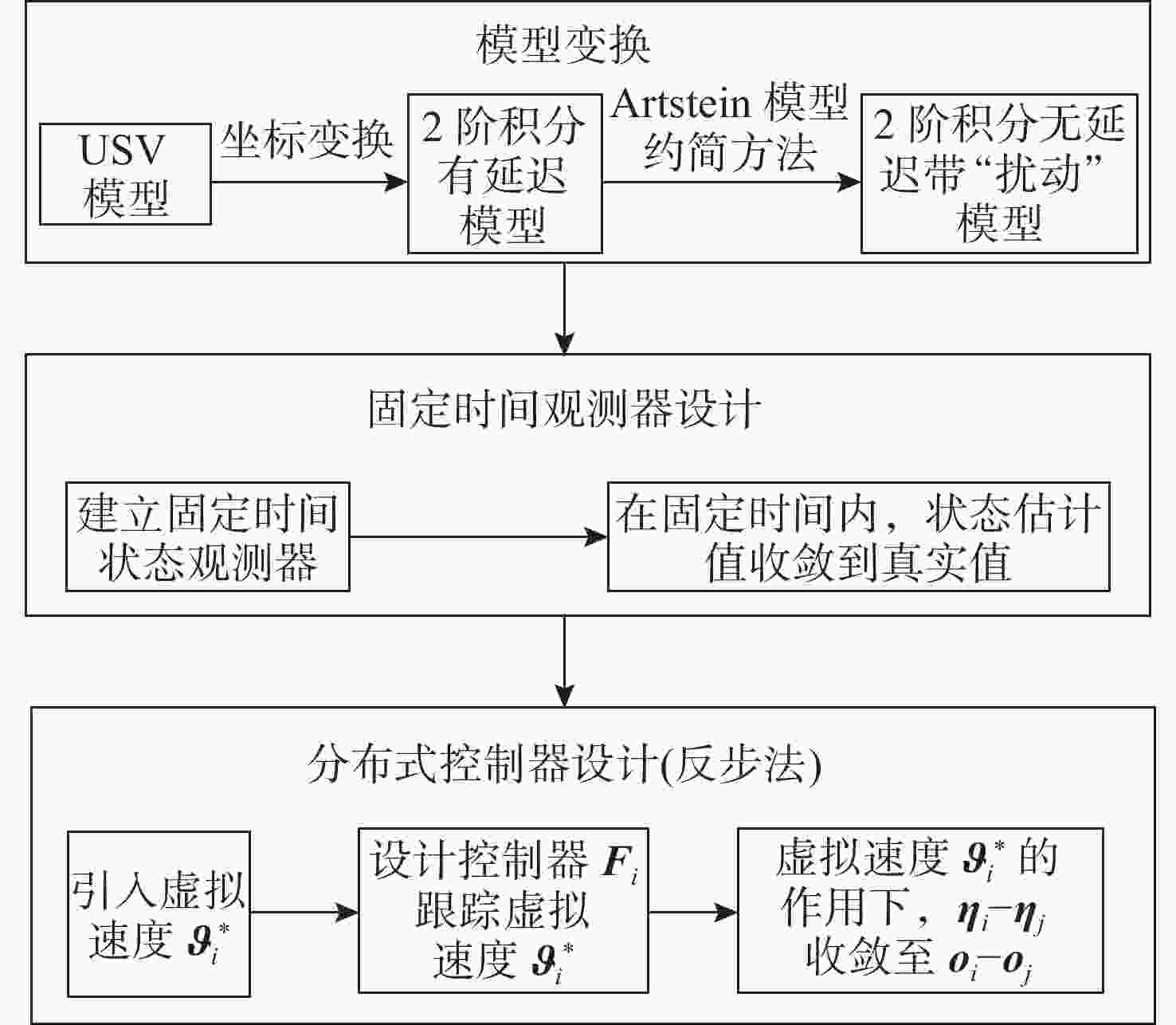
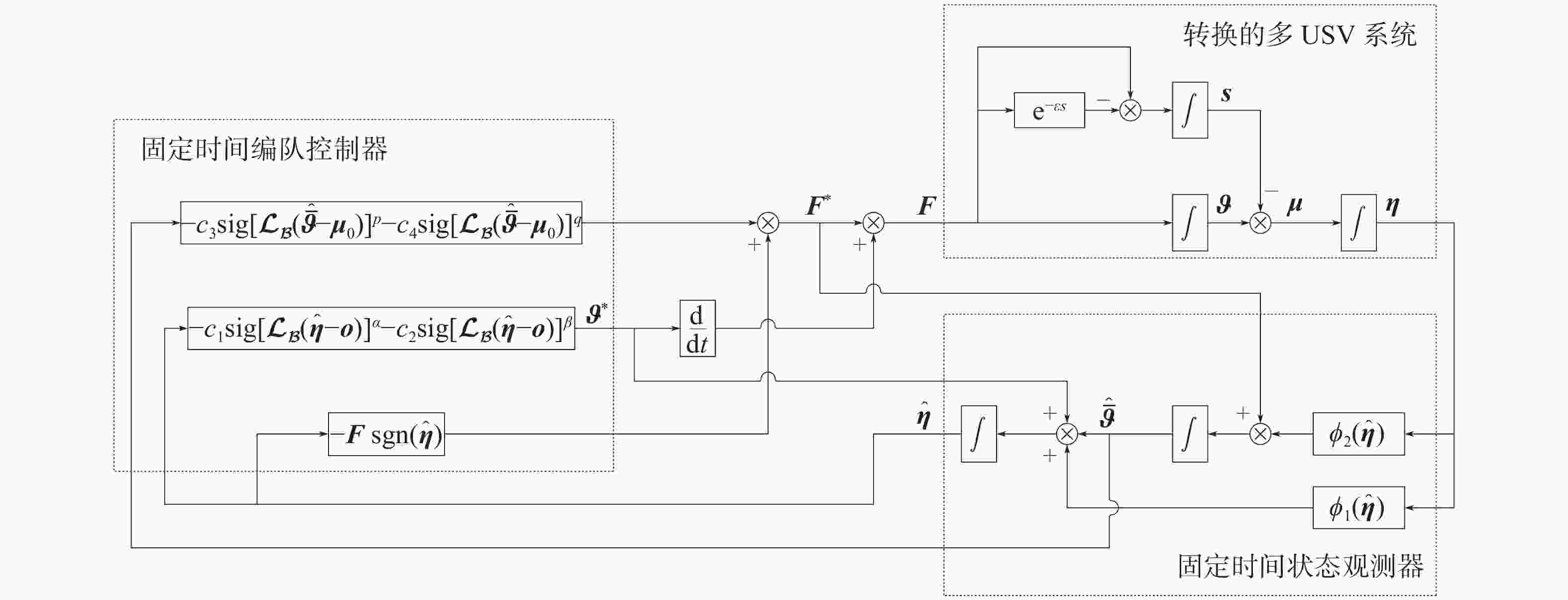
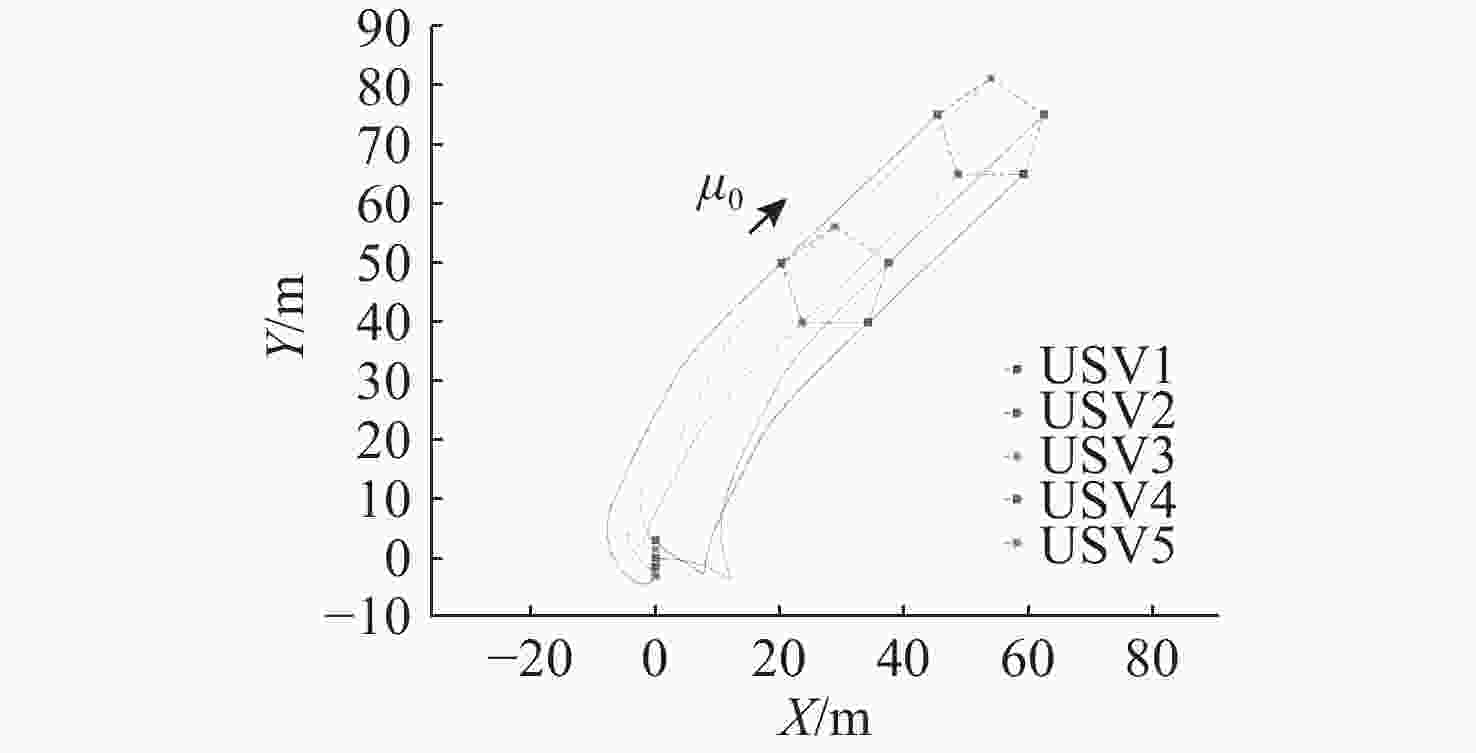
摘要: 近年来, 固定时间编队控制是多无人艇(USV)系统的研究热点, 而输入时延问题是多USV系统固定时间编队过程中亟待解决的关键科学问题之一。鉴于此, 在一般的有向交互拓扑结构下, 文中针对含有输入时延的多USV系统的固定时间编队控制问题开展了深入研究。首先, 应用Artstein约简方法将带有输入时延的多USV系统转化为具有2阶积分形式的含有扰动的控制系统。其次, 为了克服系统扰动影响, 仅使用USV的相对位置信息, 构建固定时间状态观测器对系统状态进行估计。在此基础上, 结合反步法, 提出了一种分布式固定时间编队控制协议, 实现了含有输入时延的多USV系统的固定时间编队控制。最后, 通过仿真实验验证了所提理论结果的正确性。
- 多无人艇系统 /
- 固定时间编队控制 /
- 状态观测器 /
- 输入时延
Abstract: In recent years, fixed-time formation control is a research hotspot for multi-unmanned surface vessel (USV) systems, and the input delay problem is one of the key scientific issues to be solved in the fixed-time formation process of multi-USV systems. In view of this, under the general directed interaction topology, this paper carries out an in-depth study on the fixed-time formation control problem of multi-USV systems containing input delay. Firstly, the Artstein reduction method is applied to transform a multi-USV system with input time delays into a disturbance-containing control system with a second-order integral form. Secondly, in order to overcome the effect of system disturbances, a fixed-time state observer is constructed to estimate the system state. It is worth mentioning that this state observer uses only the relative position information of the USV. On this basis, a distributed fixed-time formation control protocol is proposed in combination with the backstepping method to realize the fixed-time formation control of multi-USV systems containing input delays. Finally, the correctness of the proposed theoretical results is verified by simulation experiments.
- multi-unmanned surface ves sel systems /
- fixed-time formation control /
- state observer /
- input delay

HTML全文

图 1 USV运动的示意图

Figure 1. Illustration of USV Motion

下载: 全尺寸图片幻灯片

图 2 文中技术路线图

Figure 2. The technical line of this paper

下载: 全尺寸图片幻灯片

图 3 多USV系统的闭环控制框图

Figure 3. Control framework of the multi-USV system

下载: 全尺寸图片幻灯片

图 4 多USV系统的通信拓扑图

Figure 4. The communication topology for multi-USV systems

下载: 全尺寸图片幻灯片

图 5 编队过程中每个USV的状态曲线

Figure 5. States for each USV during the formation process

下载: 全尺寸图片幻灯片

图 6 编队过程中每个USV的状态曲线(未对系统时延进行任何处理的情况下)

Figure 6. States for each USV during the formation process (without any processing of the delay)

下载: 全尺寸图片幻灯片

图 7 多USV系统的直线编队轨迹

Figure 7. Straight line formation trajectory of the multi-USV system

下载: 全尺寸图片幻灯片

表 1 USV参数列表$(i = 1, 2, 3, 4, 5)$

Table 1. Parameters of USV$(i = 1, 2, 3, 4, 5)$

参数数值

${m_{i11}}$ 13.0 kg
${m_{i22}}$ 23.3 kg
${m_{i33}}$ 1.3 kg
${d_{i11}}$ 6.0 N
${d_{i22}}$ 7.1 N
${d_{i33}}$ 0.8 N

下载: 导出CSV

参考文献(37)

[1]	JIANG X, XIA G. Sliding mode formation control of leaderless unmanned surface vehicles with environmental disturbances[J]. Ocean Engineering, 2022, 244: 110301. doi: 10.1016/j.oceaneng.2021.110301
[2]	DONG Z, ZHANG Z, QI S, et al. Autonomous cooperative formation control of underactuated USVs based on improved MPC in complex ocean environment[J]. Ocean Engineering, 2023, 270: 113633. doi: 10.1016/j.oceaneng.2023.113633
[3]	ZHANG D, TANG Y, DING Z, et al. Event-based resilient formation control of multiagent systems[J]. IEEE Transactions on Cybernetics, 2019, 51(5): 2490-2503.
[4]	DONG X, LI Y, LU C, et al. Time-varying formation tracking for UAV swarm systems with switching directed topologies[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 30(12): 3674-3685.
[5]	HE W, YIN Z, SUN C. Adaptive neural network control of a marine vessel with constraints using the asymmetric barrier Lyapunov function[J]. IEEE Transactions on Cybernetics, 2016, 47(7): 1641-1651.
[6]	XIAO B, YANG X, HUO X. A novel disturbance estimation scheme for formation control of ocean surface vessels[J]. IEEE Transactions on Industrial Electronics, 2016, 64(6): 4994-5003.
[7]	ZHANG Y, WU Z G, SHI P. Resilient event-/self-triggering leader-following consensus control of multiagent systems against DoS attacks[J]. IEEE Transactions on Industrial Informatics, 2022, 19(4): 5925-5934.
[8]	YANG B, LI H, YAO D, et al. DO-based adaptive consensus control for multiple MUAVs with dynamic constraints[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 53(4): 2387-2398.
[9]	ZHAO Y, MA Y, HU S. USV formation and path-following control via deep reinforcement learning with random braking[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(12): 5468-5478. doi: 10.1109/TNNLS.2021.3068762
[10]	宋吉广, 李德隆, 冯亮, 等. 基于感知信息的USV目标环绕跟踪方法[J]. 水下无人系统学报, 2023, 31(5): 696-702. doi: 10.11993/j.issn.2096-3920.202206011 SONG J G, LI D L, FENG L, et al. Target surround tracking method of USVs based on perception information[J]. Journal of Unmanned Undersea Systems, 2023, 31(5): 696-702. doi: 10.11993/j.issn.2096-3920.202206011
[11]	HU B B, ZHANG H T, LIU B, et al. Distributed surrounding control of multiple unmanned surface vessels with varying interconnection topologies[J]. IEEE Transactions on Control Systems Technology, 2021, 30(1): 400-407.
[12]	LIU B, ZHANG H T, MENG H, et al. Scanning-chain formation control for multiple unmanned surface vessels to pass through water channels[J]. IEEE Transactions on Cybernetics, 2020, 52(3): 1850-1861.
[13]	XIE W, MA B, FERNANDO T, et al. A new formation control of multiple underactuated surface vessels[J]. International Journal of Control, 2018, 91(5): 1011-1022. doi: 10.1080/00207179.2017.1303849
[14]	QU Y, CAI L. An adaptive delay-compensated filtering system and the application to path following control for unmanned surface vehicles[J]. ISA Transactions, 2023, 136: 548-559. doi: 10.1016/j.isatra.2022.10.041
[15]	LIANG X, ZHANG Y, YANG G. Platoon control design for unmanned surface vehicles subject to input delay[J]. Scientific Reports, 2021, 11(1): 1481. doi: 10.1038/s41598-020-80348-4
[16]	高伟, 杨建, 刘菊, 等. 考虑通信延迟的多水面无人艇协同定位算法[J]. 哈尔滨工程大学学报, 2013, 34(12): 1490-1496, 1513. doi: 10.3969/j.issn.1006-7043.201301057 GAO W, YANG J, LIU J, et al. Cooperative location of multiple unmanned surface vessels(USVs) considering communication delay[J]. Journal of Harbin Engineering University, 2013, 34(12): 1490-1496, 1513. doi: 10.3969/j.issn.1006-7043.201301057
[17]	陈昱衡, 张海成, 邹伟生, 等. 考虑系统延时的无人船路径跟踪控制[J]. 中国造船, 2023, 64(5): 249-258. doi: 10.3969/j.issn.1000-4882.2023.05.021 CHEN Y H, ZHANG H C, ZOU W S, et al. Path tracking control algorithm of unmanned ship considering system delay[J]. Shipbuilding of China, 2023, 64(5): 249-258. doi: 10.3969/j.issn.1000-4882.2023.05.021
[18]	陈立家, 周为, 许毅, 等. 一种基于SDN的多约束无人船网络传输路由算法[J]. 中国舰船研究, 2022, 17(4): 107-113. CHEN L J, ZHOU W, XU Y, et al. Multi-constrained unmanned surface vessel network transmission routing algorithm based on SDN[J]. Chinese Journal of Ship Research, 2022, 17(4): 107-113.
[19]	CHEN D, LIU X, YU W. Finite-time fuzzy adaptive consensus for heterogeneous nonlinear multi-agent systems[J]. IEEE Transactions on Network Science and Engineering, 2020, 7(4): 3057-3066. doi: 10.1109/TNSE.2020.3013528
[20]	JIN X, SHI Y, TANG Y, et al. Event-triggered fixed-time attitude consensus with fixed and switching topologies[J]. IEEE Transactions on Automatic Control, 2021, 67(8): 4138-4145.
[21]	HUANG B, SONG S, ZHU C, et al. Finite-time distributed formation control for multiple unmanned surface vehicles with input saturation[J]. Ocean Engineering, 2021, 233: 109158. doi: 10.1016/j.oceaneng.2021.109158
[22]	WANG Y, LIU C. Distributed finite-time adaptive fault-tolerant formation-containment control for USVs with dynamic event-triggered mechanism[J]. Ocean Engineering, 2023, 280: 114524. doi: 10.1016/j.oceaneng.2023.114524
[23]	WU W, TONG S. Fixed-time formation fault tolerant control for unmanned surface vehicle systems with intermittent actuator faults[J]. Ocean Engineering, 2023, 281: 114813. doi: 10.1016/j.oceaneng.2023.114813
[24]	DUAN H, YUAN Y, ZENG Z. Distributed robust learning control for multiple unmanned surface vessels with fixed-time prescribed performance[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2024, 54(2): 787-799. doi: 10.1109/TSMC.2023.3321119
[25]	LIU H, WENG P, TIAN X, et al. Distributed adaptive fixed-time formation control for UAV-USV heterogeneous multi-agent systems[J]. Ocean Engineering, 2023, 267: 113240. doi: 10.1016/j.oceaneng.2022.113240
[26]	HUANG D, LI H, LI X. Formation of generic UAVs-USVs system under distributed model predictive control scheme[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(12): 3123-3127.
[27]	QU Y, ZHAO W, YU Z, et al. Distributed prescribed performance containment control for unmanned surface vehicles based on disturbance observer[J]. ISA Transactions, 2022, 125: 699-706. doi: 10.1016/j.isatra.2021.12.007
[28]	WEI X, YU W, WANG H, et al. An observer-based fixed-time consensus control for second-order multi-agent systems with disturbances[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 66(2): 247-251.
[29]	ZUO Z, TIE L. A new class of finite-time nonlinear consensus protocols for multi-agent systems[J]. International Journal of Control, 2014, 87(2): 363-370. doi: 10.1080/00207179.2013.834484
[30]	POLYAKOV A. Nonlinear feedback design for fixed-time stabilization of linear control systems[J]. IEEE Transactions on Automatic Control, 2011, 57(8): 2106-2110.
[31]	SÁNCHEZ-TORRES J D, LOUKIANOV A G. A fixed-time second order sliding mode observer for a class of nonlinear systems[C]//2014 13th International Workshop on Variable Structure Systems. Nantes, France: IEEE, 2014.
[32]	DO K D, PAN J. Control of ships and underwater vehicles: Design for underactuated and nonlinear marine systems[M]. Berlin: Springer Science & Business Media, 2009.
[33]	WANG C, ZUO Z, LIN Z, et al. Consensus control of a class of lipschitz nonlinear systems with input delay[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2015, 62(11): 2730-2738. doi: 10.1109/TCSI.2015.2479046
[34]	NI J, LIU L, LIU C, et al. Fixed-time leader-following consensus for second-order multiagent systems with input delay[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8635-8646. doi: 10.1109/TIE.2017.2701775
[35]	SHTESSEL Y, EDWARDS C, FRIDMAN L, et al. Sliding mode control and observation[M]. New York: Springer New York, 2014.
[36]	ZHANG H, LI Z, QU Z, et al. On constructing Lyapunov functions for multi-agent systems[J]. Automatica, 2015, 58: 39-42. doi: 10.1016/j.automatica.2015.05.006
[37]	WANG W, MATEOS L A, PARK S, et al. Design, modeling, and nonlinear model predictive tracking control of a novel autonomous surface vehicle[C]//IEEE International Conference on Robotics and Automation. Brisbane, Australia: IEEE, 2018: 6189-6196.