Numerical Simulation of Water Entry Process of Trans-Medium Vehicles
-
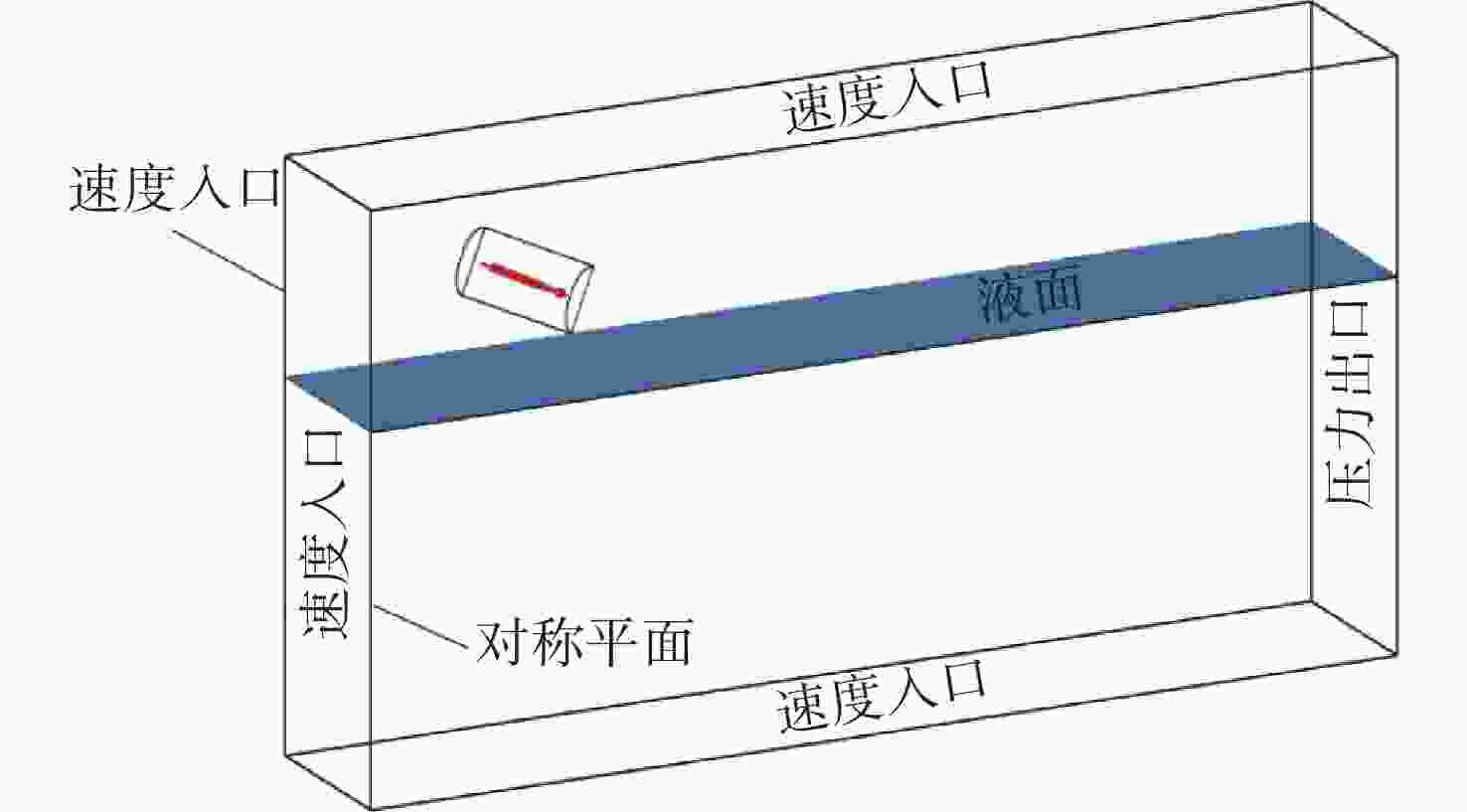
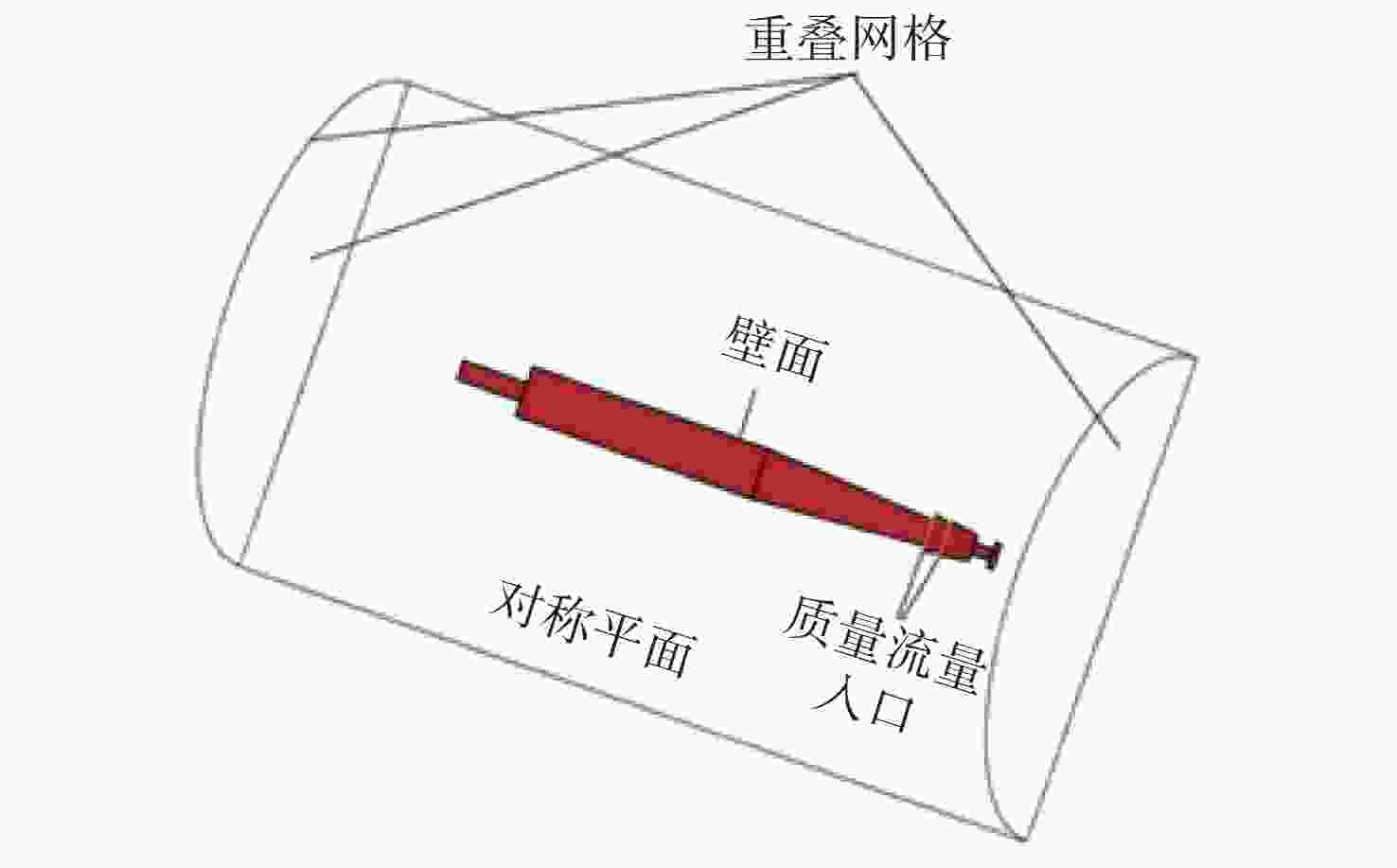
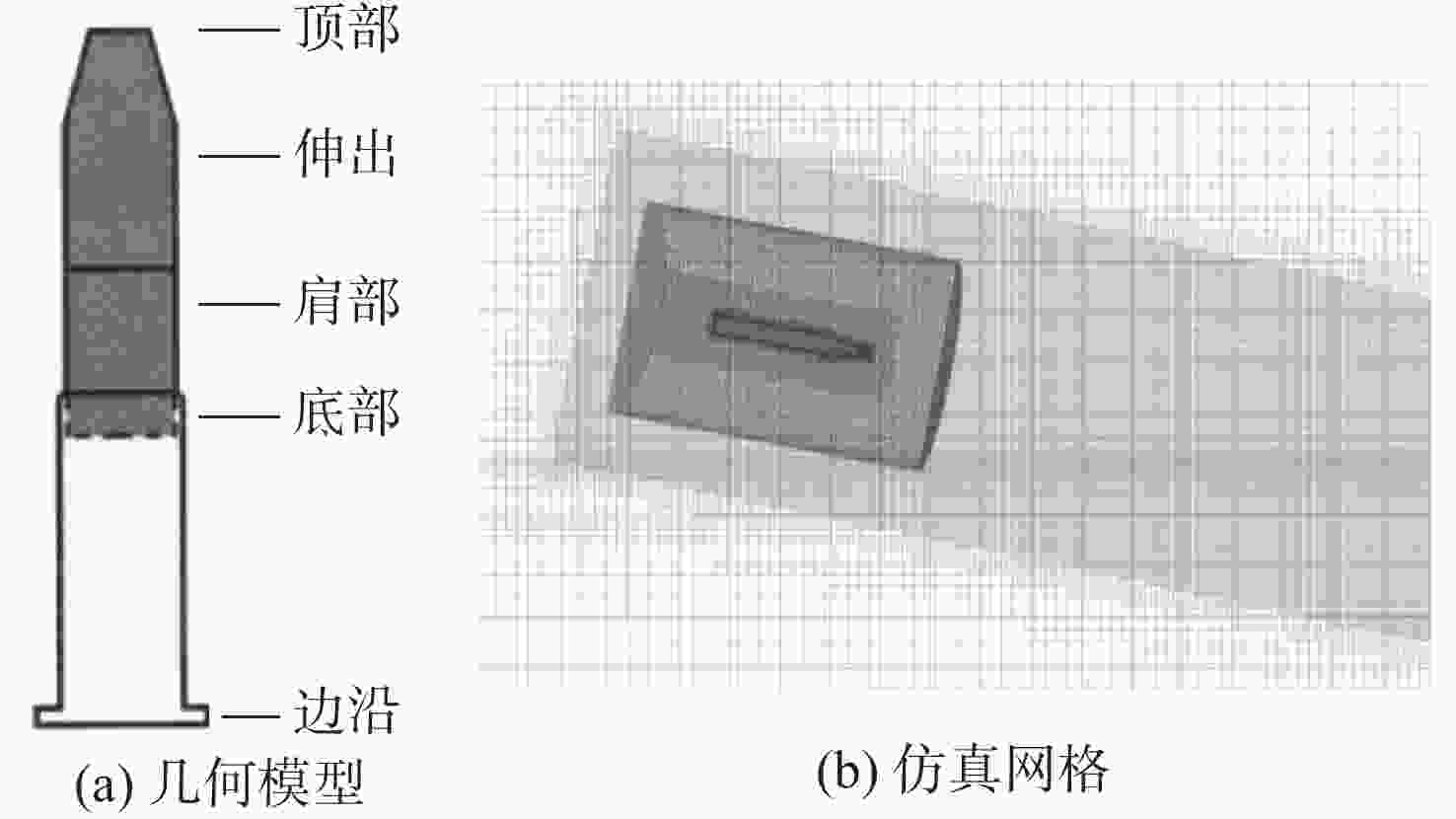
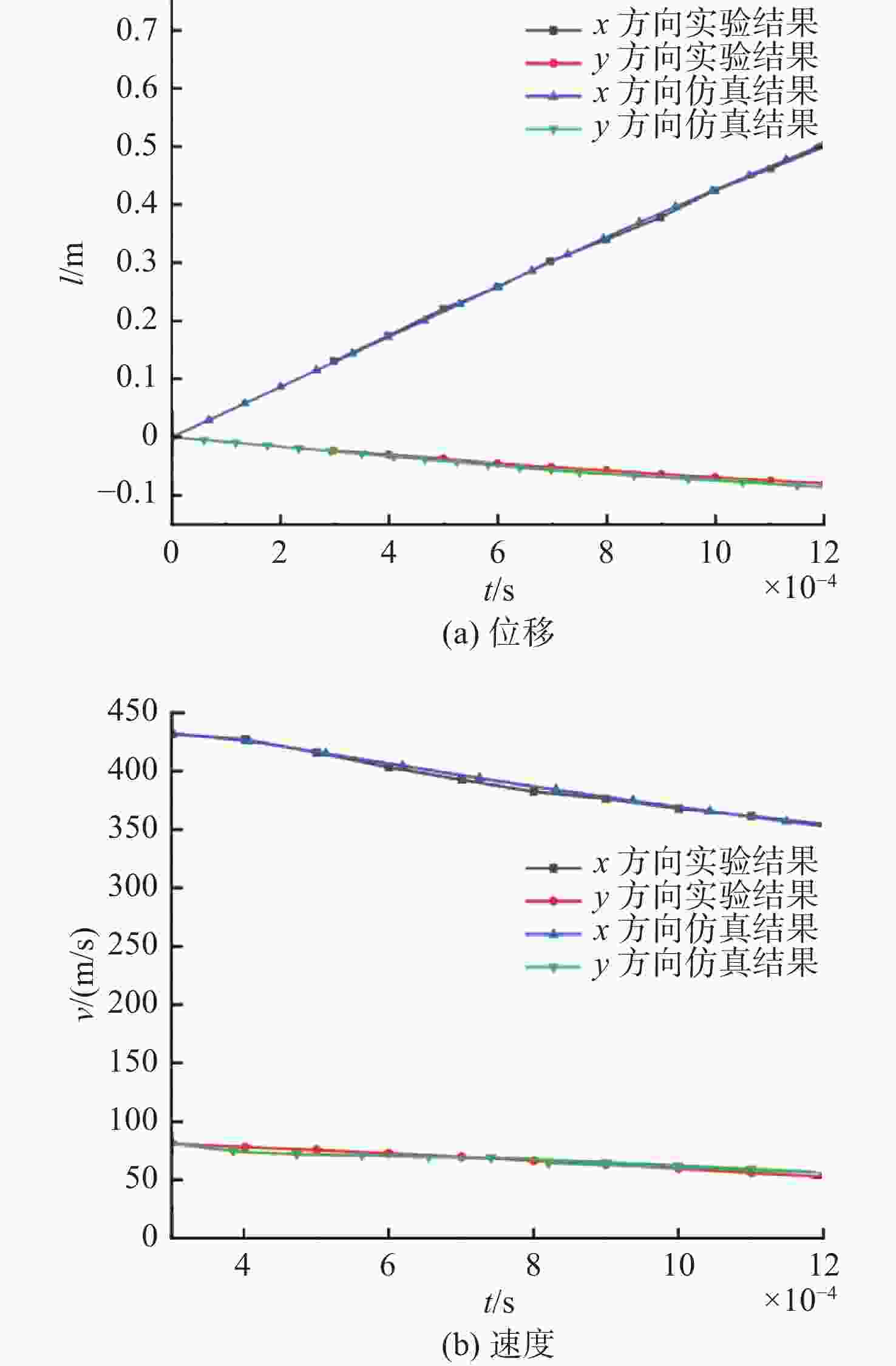
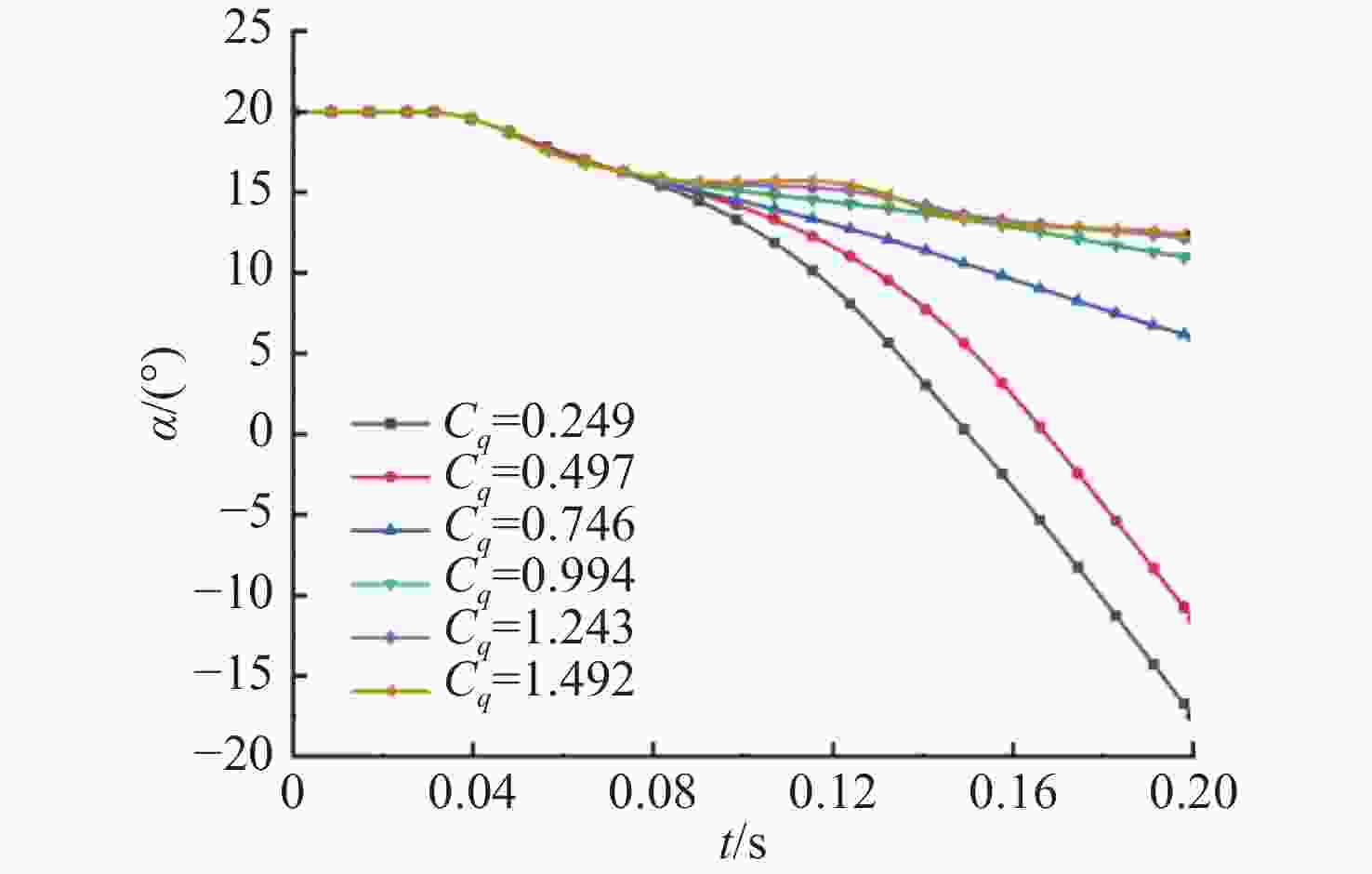
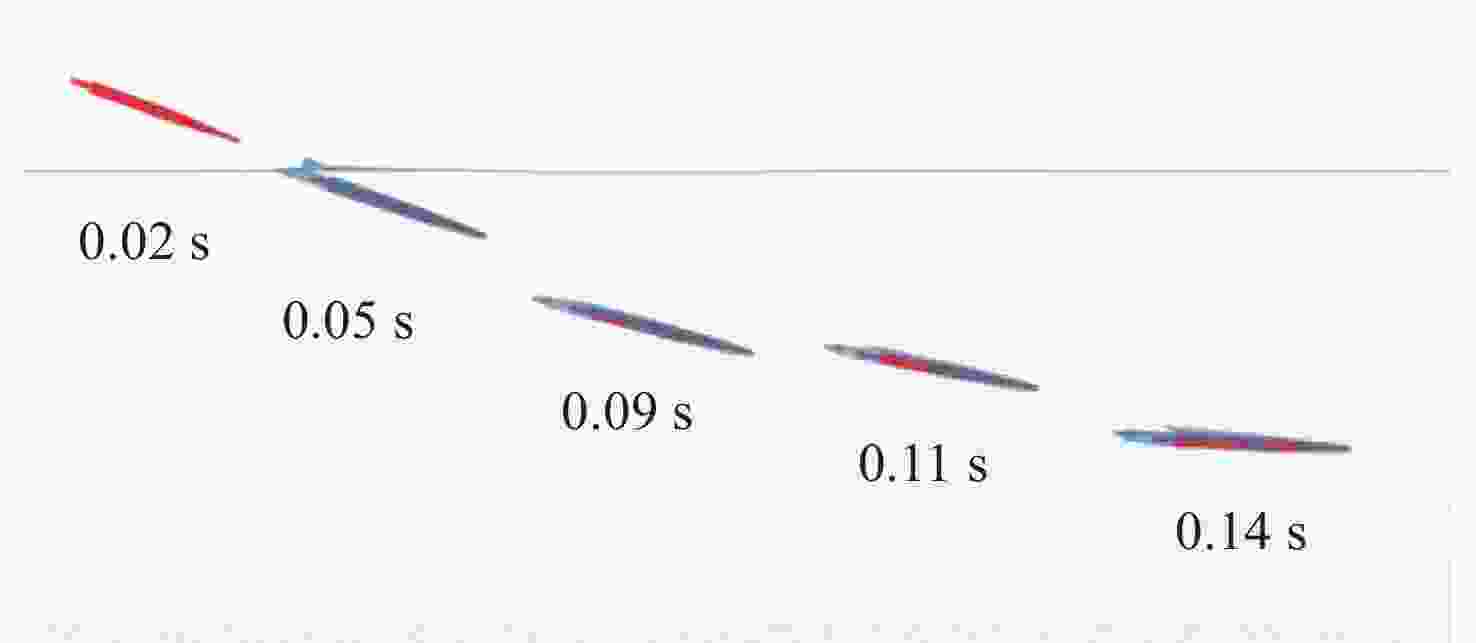
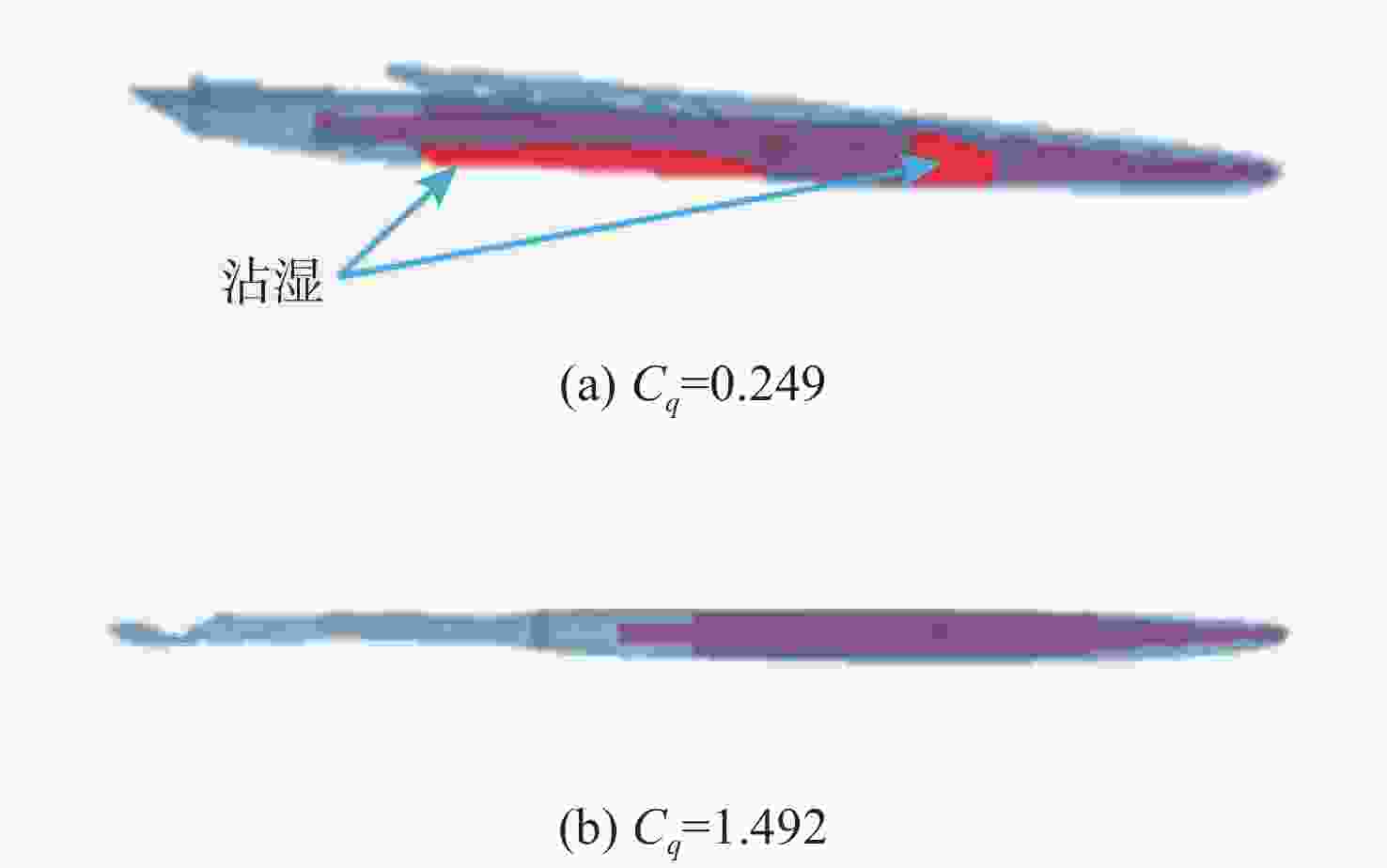
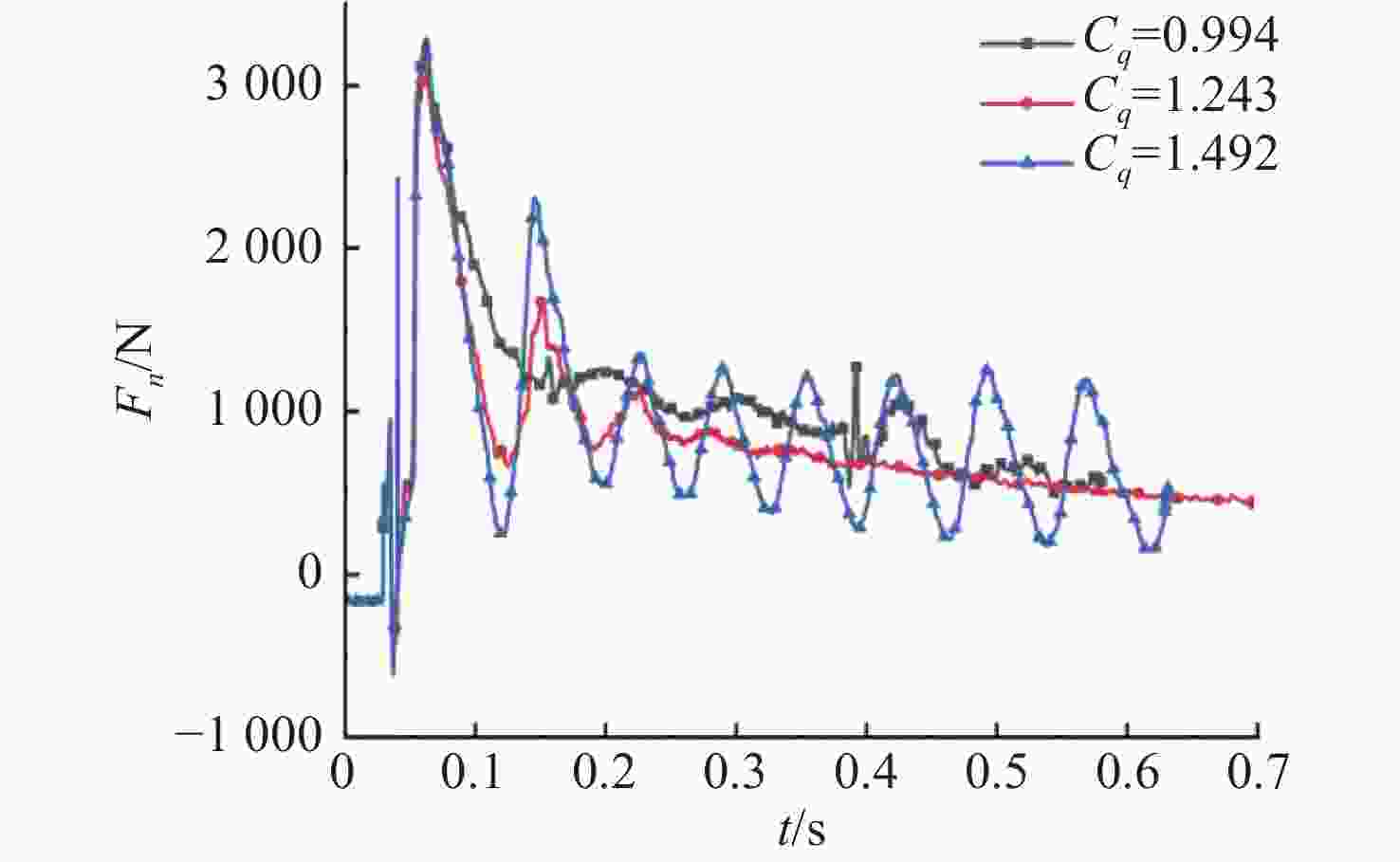
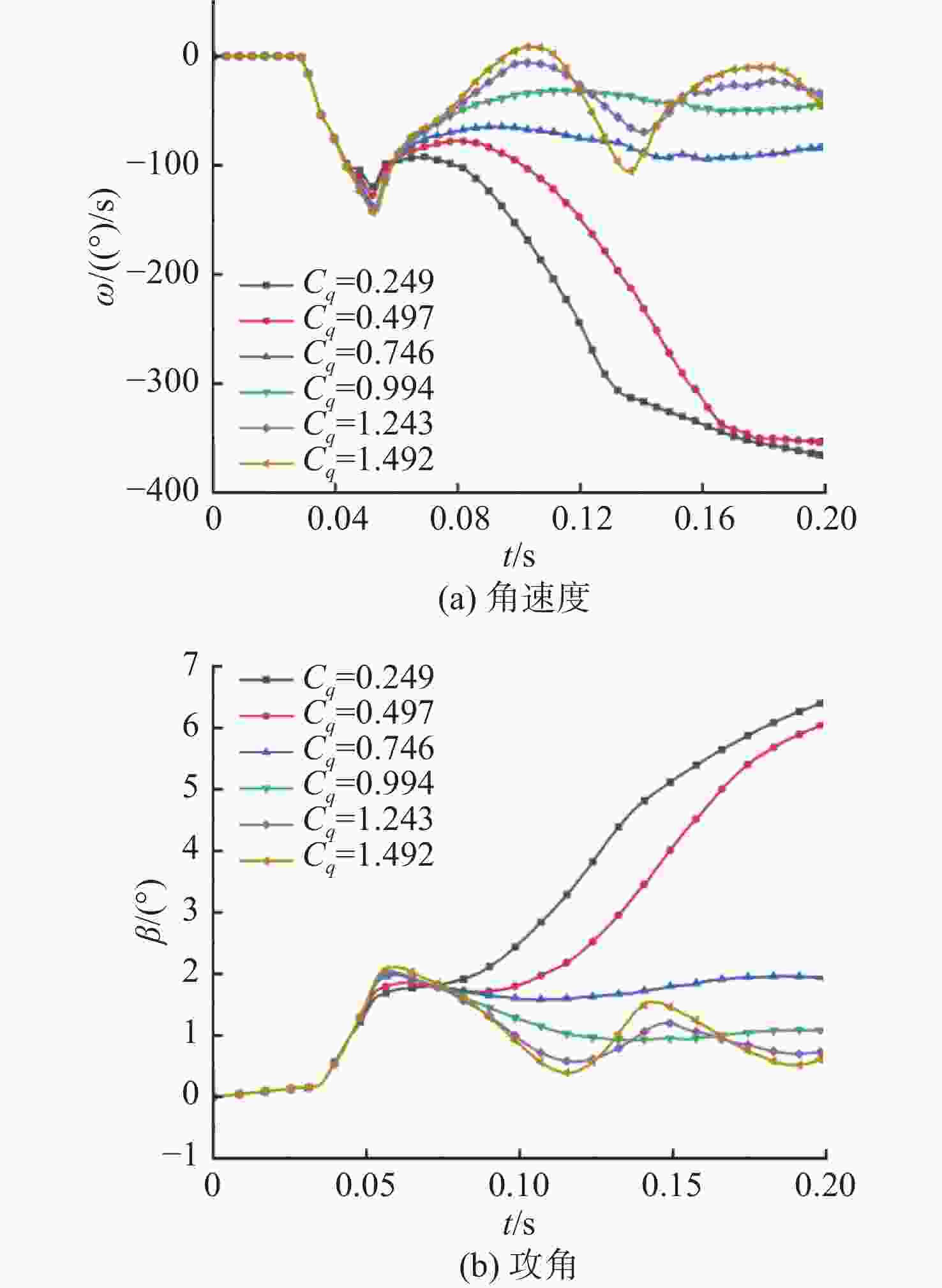
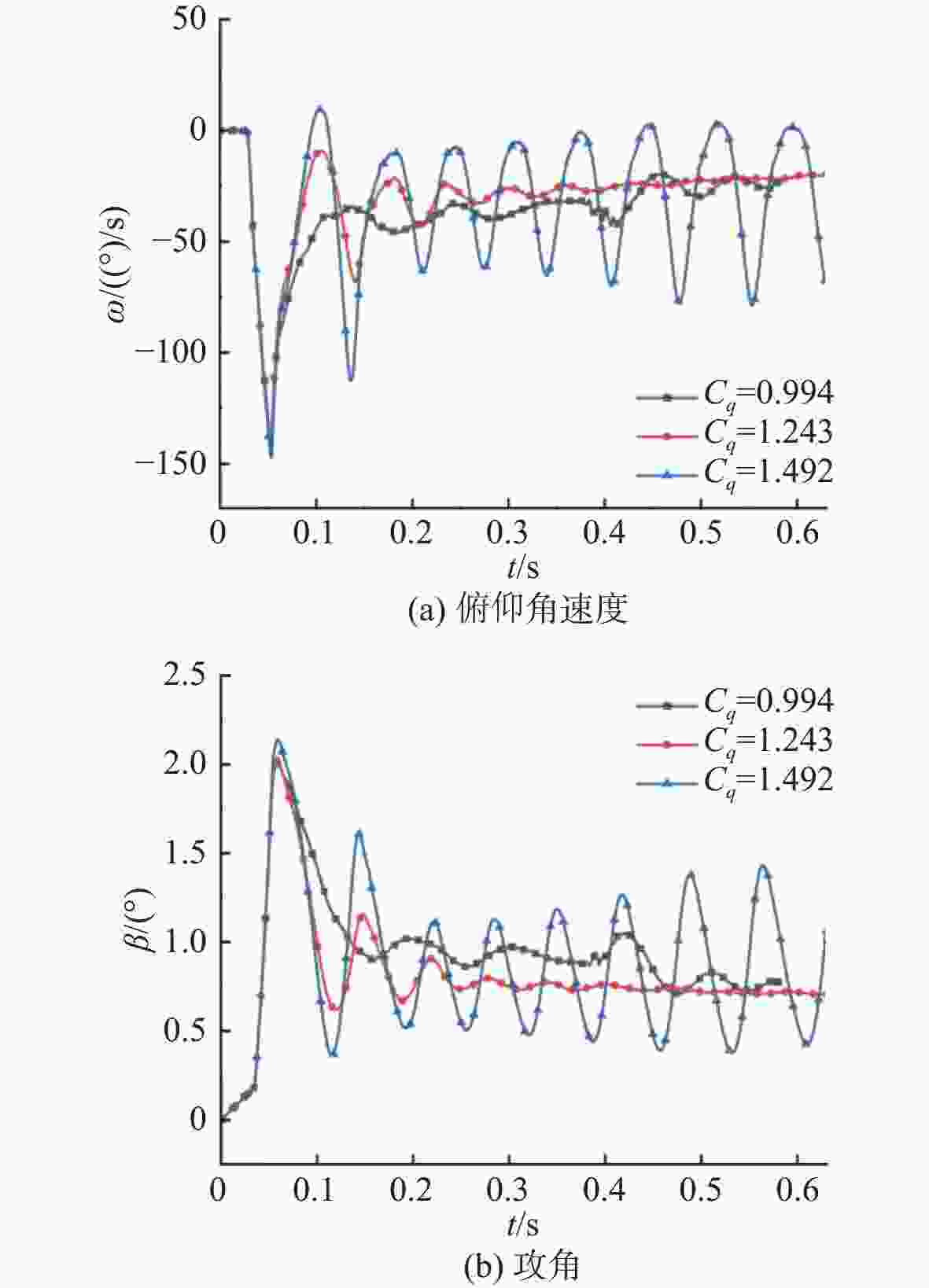
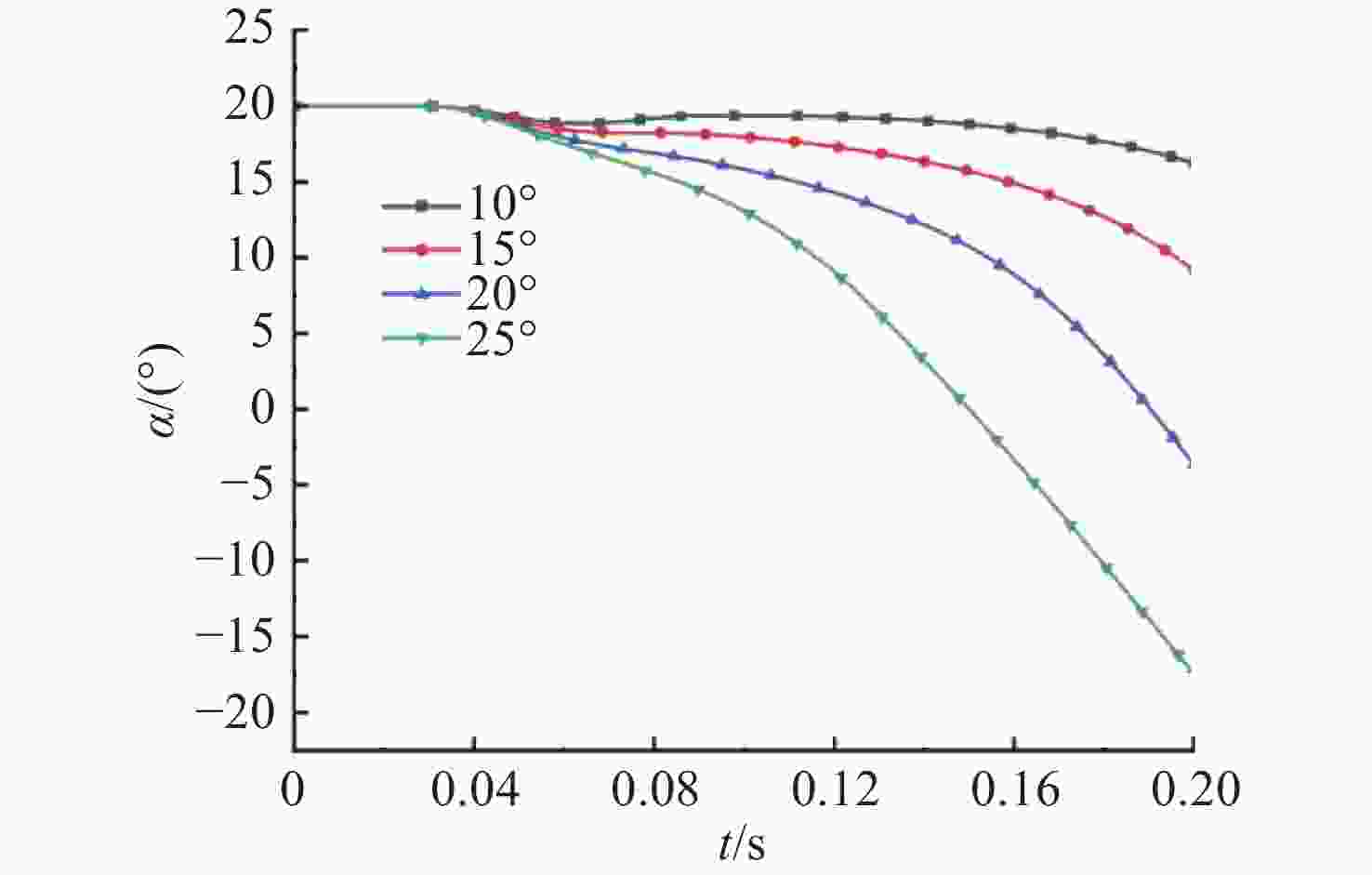
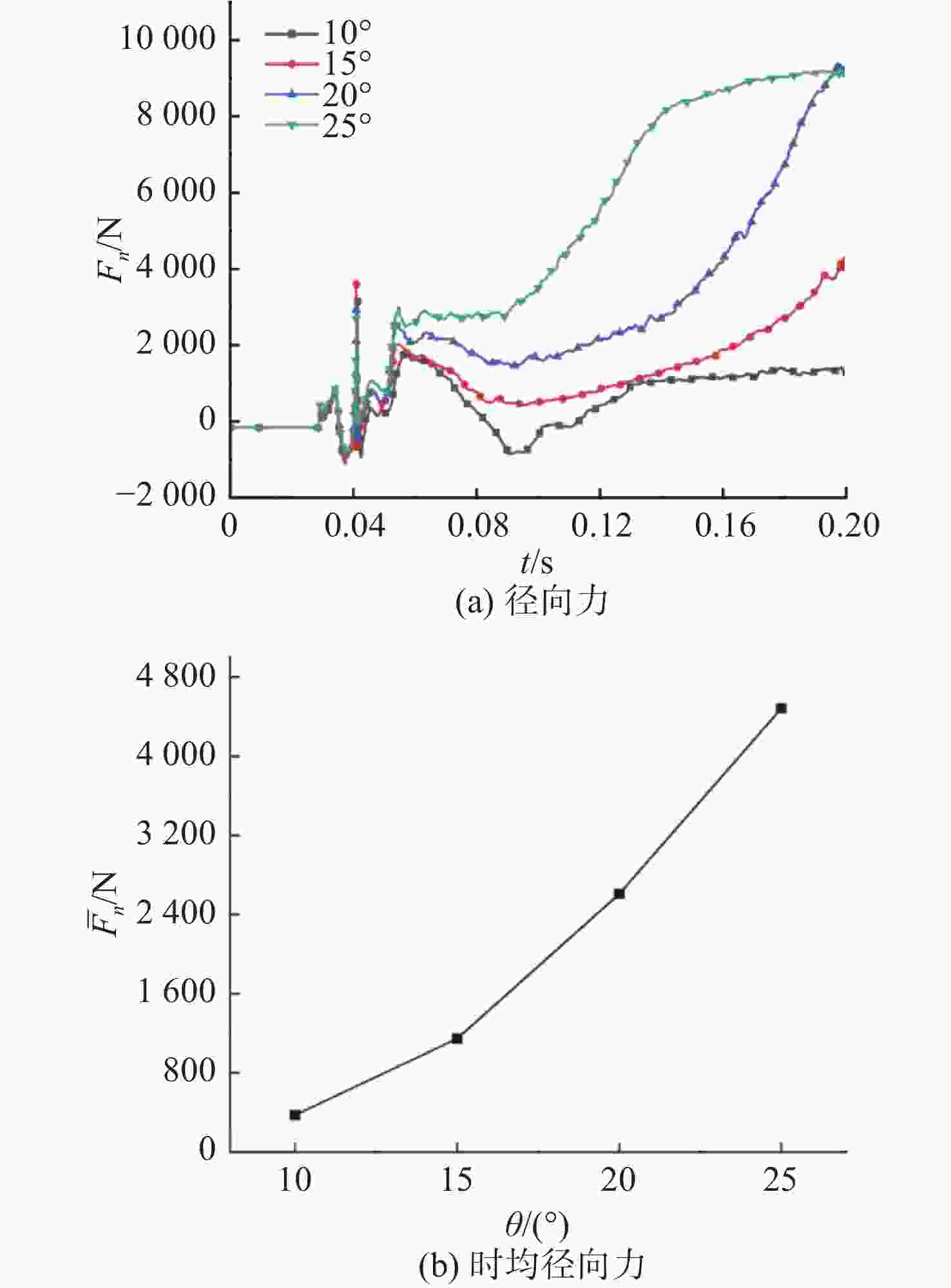
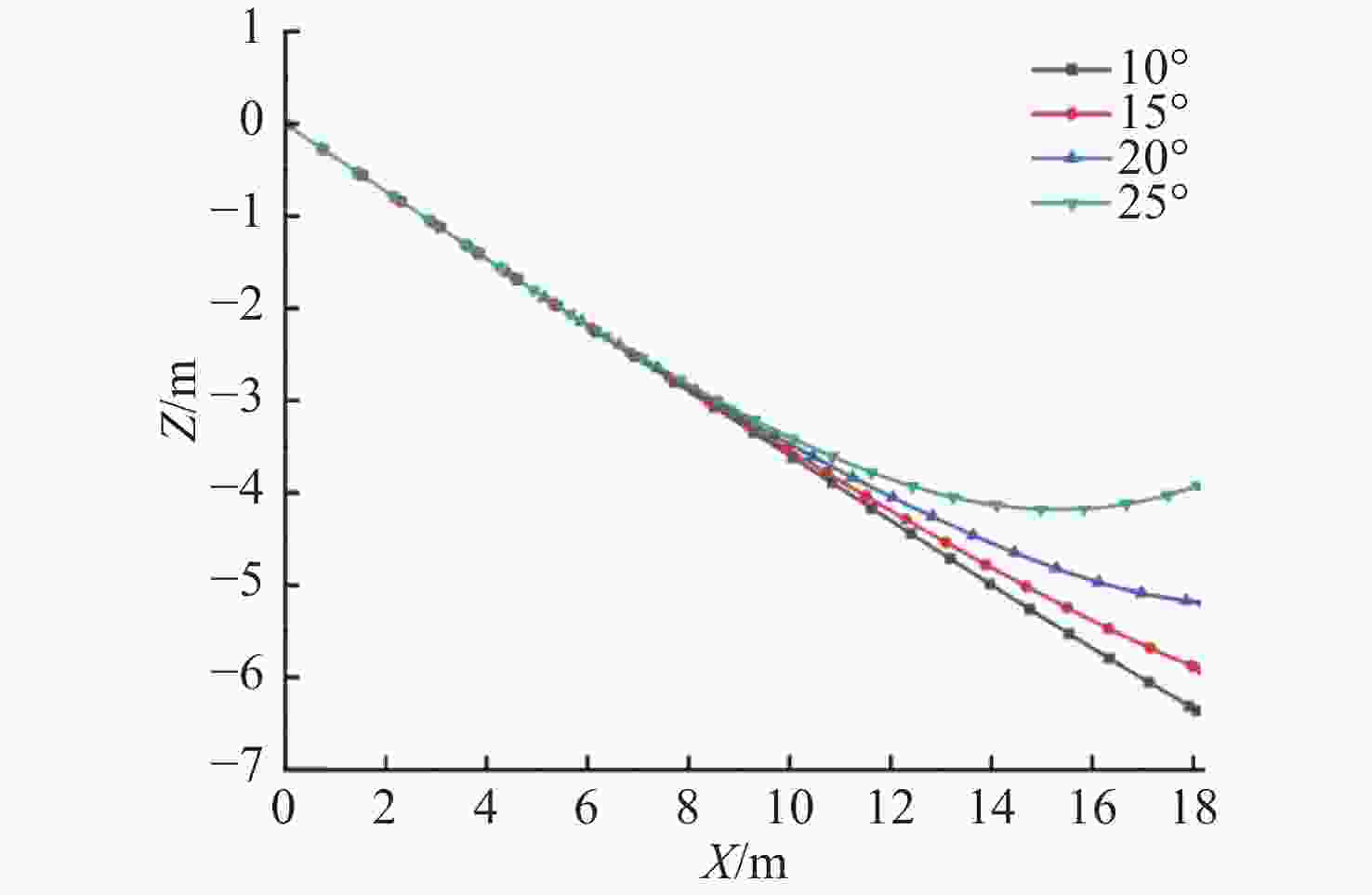
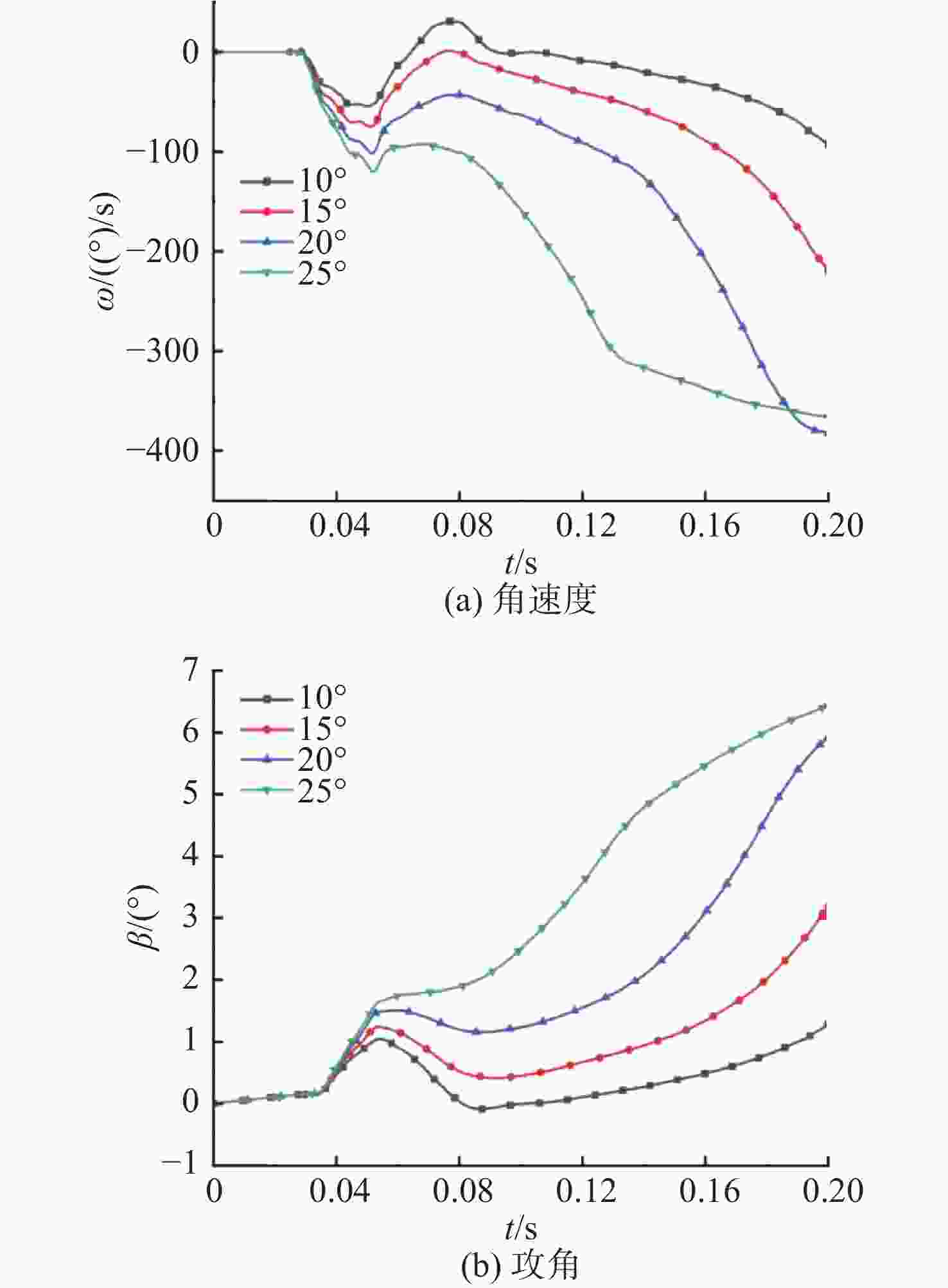
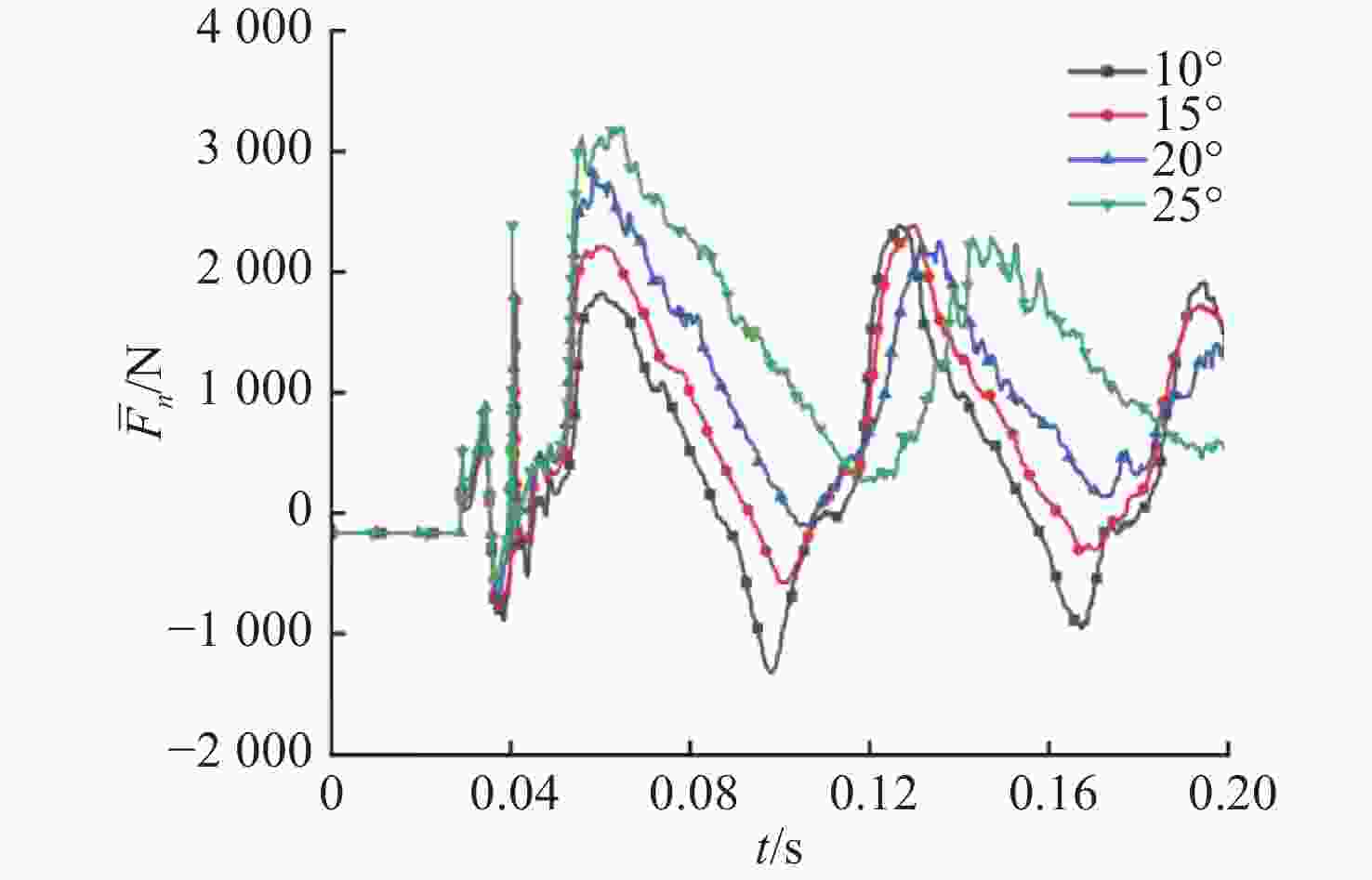
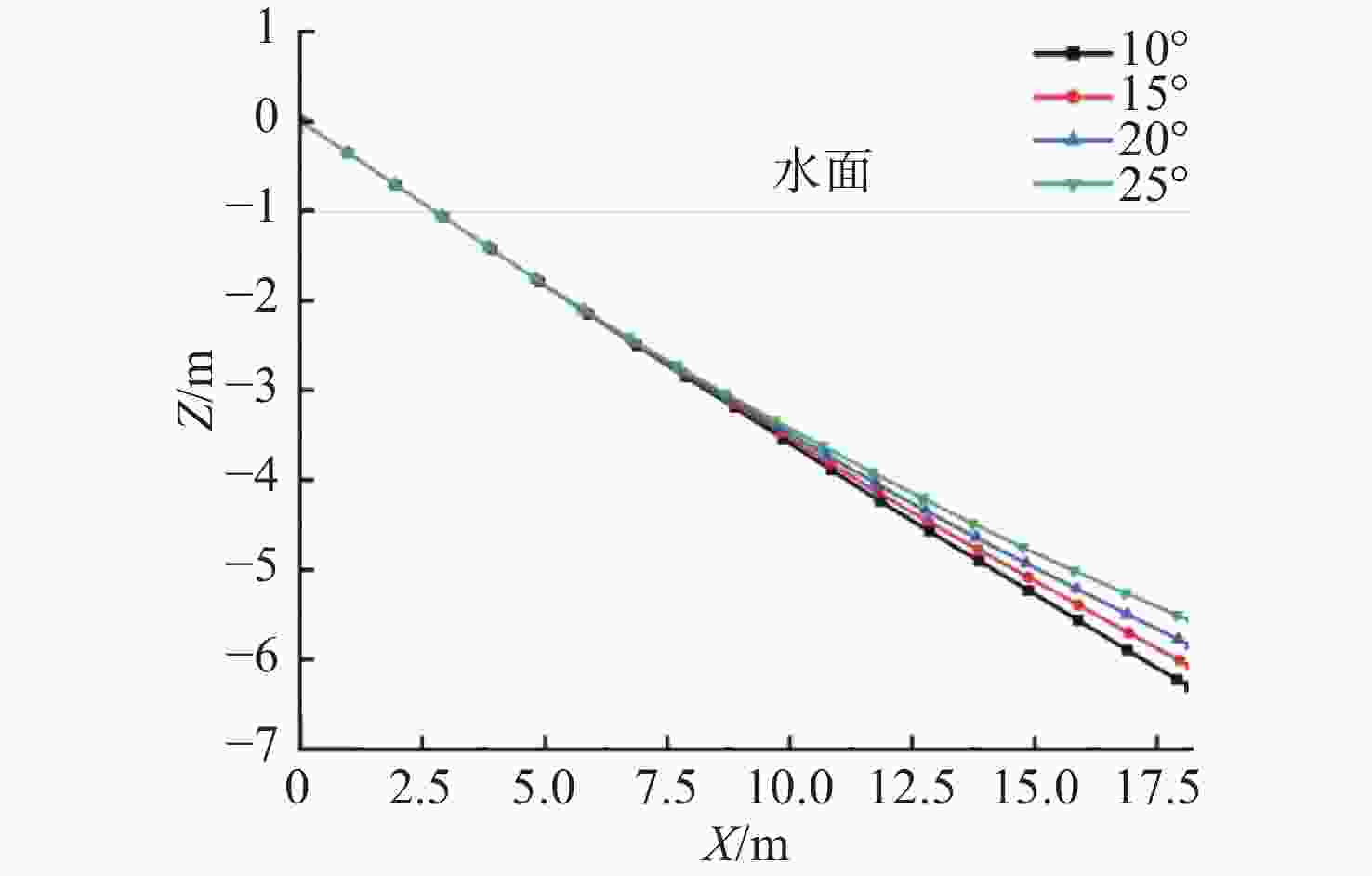
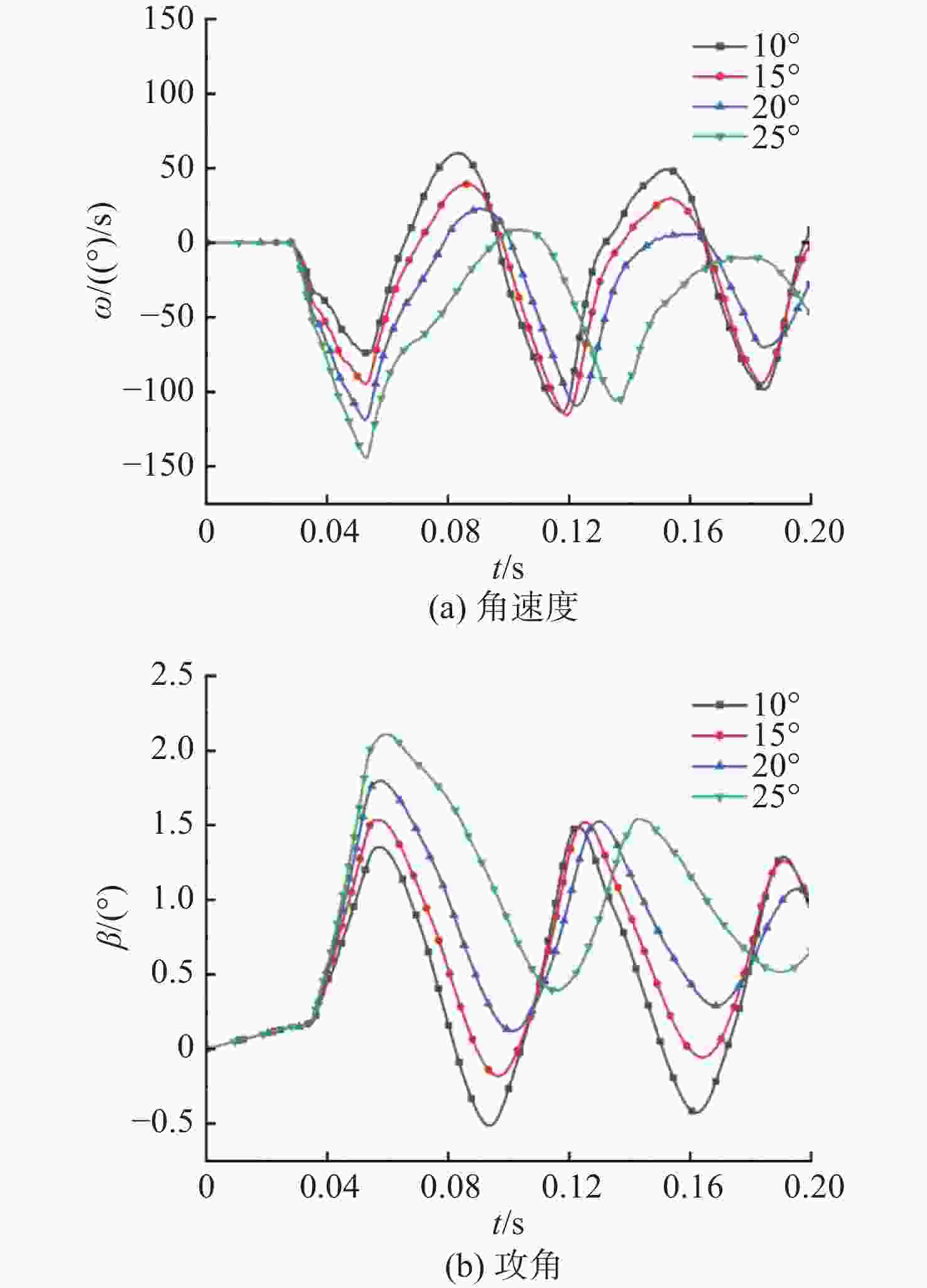
摘要: 航行器跨介质入水过程往往伴随着多相流、空化、相变及湍流不稳定性, 不仅会加剧流场的复杂性, 还使其所受的作用力呈现出较强的非定常性和非线性。文中建立了航行器入水过程的数值计算模型, 采用流体体积模型捕捉气液交界面, 使用Schnerr-Sauer模型对跨介质过程中产生的空化过程进行描述。对不同通气量和空化器倾角下的跨介质航行器入水过程进行仿真计算, 研究了跨介质过程中的流场和空泡演化规律, 分析并得到了航行器跨介质过程中的流体动力学特性以及运动特性。仿真结果表明, 航行器在入水过程中会随着通气量的变化而呈现出2种不同的姿态变化模式: 增角速度拉平模式和周期俯仰式拉平模式, 不同模式下航行器的入水拉平过程会呈现不同运动特点；此外, 空化器倾角的增加和通气量的降低可以提高航行器在跨介质入水过程中的姿态变化速率。Abstract: The trans-medium water entry process of vehicles is often accompanied by multiphase flow, cavitation, phase change, and turbulence instability, which not only heighten the complexity of the flow field, but also render the forces highly unsteady and nonlinear. A numerical model for the water entry process of vehicles was developed. The volume of fluid(VOF) model was employed to capture the gas-liquid interface, and the Schnerr-Sauer model was utilized to describe the cavitation that occurred during the trans-medium process. The simulation of the water entry process of the trans-medium vehicle under different ventilation flows and deflection angles of the cavitator was carried out to investigate the flow field and cavity evolution laws during the trans-medium process. In addition, the fluid dynamics characteristics, as well as the kinematic characteristics of the vehicle during trans-medium process were analyzed. The simulation results show that the vehicle will present two different attitude change modes with the change of the ventilation flow during the water entry process: the increasing angular velocity leveling mode and the periodical pitching-type leveling mode. The water entry leveling process of the vehicle in different modes will show different motion characteristics. Moreover, an increase in the deflection angle of the cavitator and a decrease in the ventilation flow can improve the attitude change rate of the vehicle during the trans-medium water entry process.
-
Key words:
- trans-medium vehicle /
- water entry /
- ventilation flow /
- deflection angle of cavitator
-
图 3 航行器区域边界条件示意图
Figure 3. Schematic diagram of the boundary conditions of the vehicle region
图 5 试验弹入水试验与仿真的气液交界面变化
Figure 5. Variation of gas-liquid interface between the test projectile in water test and simulation
图 7 不同网格数量下航行器径向力矩时变曲线
Figure 7. Time-varying curves of radial torque of the vehicle under different number of grids
图 8 不同网格数量下航行器速度时变曲线
Figure 8. Time-varying curves of velocity of the vehicle under different number of grids
图 9 不同网格数量下航行器位移时变曲线
Figure 9. Time-varying curves of displacement of the vehicle under different number of grids
图 11 不同通气量下航行器俯仰角变化曲线
Figure 11. Curves of pitch angle of the vehicle under different ventilation
图 12 工况1条件下航行器典型时刻空泡图
Figure 12. Cavity diagram of the vehicle under operating condition 1 at typical moments
图 13 不同通气量下拉平时刻空泡轮廓
Figure 13. Cavity outline at flattening time under different ventilation
图 14 不同通气量下航行器入水弹道曲线
Figure 14. Water entry trajectory curves of vehicle under different ventilation
图 15 不同通气量下航行器径向力时变曲线
Figure 15. Time-varying curves of radial force of vehicle under different ventilation
图 16 大通气量下航行器径向力时变曲线
Figure 16. Time-varying curves of radial force of vehicle under high ventilation
图 17 不同通气量下航行器角速度和攻角时变曲线
Figure 17. Time-varying curves of vehicle angular velocity and angle of attack under different ventilation
图 18 大通气量下航行器角速度和攻角时变曲线
Figure 18. Time-varying curves of vehicle angular velocity and angle of attack under high ventilation
图 19 不同空化器倾角下航行器俯仰角时变曲线
Figure 19. The time-varying curves of the pitch angle of the vehicle under different deflection angles of the cavitator
图 20 不同空化器倾角下航行器径向力变化曲线
Figure 20. Radial force curves of the vehicle under different deflection angles of the cavitator
图 21 不同空化器倾角下航行器入水弹道曲线
Figure 21. Water-entry trajectory curves of the vehicle under different deflection angles of the cavitator
图 22 不同空化器倾角下航行器角速度和攻角时变曲线
Figure 22. Time-varying curves of angular velocity and angle of attack of the vehicle under different deflection angles of the cavitator
图 23 不同空化器倾角下航行器径向力时变曲线
Figure 23. Time-varying curves of radial force of the vehicle under different deflection angles of the cavitator
图 24 不同空化器倾角下航行器入水弹道曲线
Figure 24. Water-entry trajectory curves for the vehicle under different deflection angles of the cavitator
图 25 不同空化器倾角下航行器角速度和攻角时变曲线
Figure 25. Time-varying curves of vehicle angular velocity and angle of attack under different deflection angles of the cavitator
表 1 不同通气流量计算工况表
Table 1. Calculation conditions under different ventilation
工况 通气
系数入水角度/(°) 空化器
倾角/(°)初始速度
/(m/s)1 0.249 20 25 100 2 0.497 3 0.746 4 0.994 5 1.243 6 1.492 
下载: 导出CSV
表 2 不同空化器倾角及小通气量下计算工况
Table 2. Calculation working conditions under different deflectiong angles of the cavitator and low ventilaion
工况 空化器倾角
/(°)入水角度
/(°)通气系数 初始速度
/(m/s)1 10 20 0.249 100 2 15 3 20 4 25
下载: 导出CSV
表 3 不同空化器倾角、大通气量条件下计算工况
Table 3. Calculation working conditions under different deflectiong angles of the cavitator and high ventilaion
工况标记 空化器角度
/(°)入水角度
/(°)通气系数 初始速度
/(m/s)1 10 20 1.492 100 2 15 3 20 4 25
下载: 导出CSV
-
[1] 魏洪亮, 陆宏志, 赵静, 等. 水下发射航行器跨介质动态载荷预报研究[J]. 导弹与航天运载技术, 2016(2): 77-80. [2] Karman T V. The impact of seaplane floats during landing: NACA-TN-321[R]. Washington, US: National Technical Information Service, 1929. [3] Wagner H. Phenomena associated with impacts and sliding on liquid surfaces[J]. J. Appl. Math. Mech, 1932, 12(4): 193-215. [4] Yu Y T. Virtual masses of rectangular plates and parallelepipeds in water[J]. Journal of Applied Physics, 1945, 16(11): 724-729. doi: 10.1063/1.1707527 [5] Watanabe I. Analytical expression of hydrodynamic impact pressure by matched asymptotic expansion technique[J]. Transactions of the West-Japan Society of Naval Architects, 1986, 71: 77-85. [6] Logvinovich G V. Hydrodynamics of flows with free boundaries[M]. New York: Halsted Press, 1973 [7] Worthington A M, Cole R S. Impact with a liquid surface, studied by the aid of instantaneous photography[J]. Proceedings of the Royal Society of London. 1899, 65(1): 153-154. [8] Truscott T T. Cavity dynamics of water entry for spheres and ballistic projectiles[D]. Boston: Massachusetts Institute of Technology, 2009. [9] 杨晓光, 党建军, 王鹏, 等. 波浪对航行器高速入水载荷特性影响[J]. 兵工学报, 2022, 43(2): 355-362.Yang Xiaoguang, Dang Jianjun, Wang Peng, et al. The influence of waves on the impact load during high-speed water-entry of a vehicle[J]. Acta Armamentarii, 2022, 43(2): 355-362. [10] 周可, 黄振贵, 陈志华, 等. 跨介质航行器高速斜入水跳弹现象研究[J]. 装备环境工程, 2022, 19(5): 39-48. doi: 10.7643/issn.1672-9242.2022.05.005 [11] Jiang Y H, Zou Z H, Li J, et al. Numerical analysis of a ventilated supercavity under periodic motion of the cavitator[J]. Journal of Hydrodynamics, 2021, 33(6): 1216-1229. doi: 10.1007/s42241-021-0103-z [12] Zhang Q, Zong Z, Sun T Z, et al. Characteristics of cavity collapse behind a high-speed projectile entering the water[J]. Physics of Fluids, 2021, 33(6): 62110. doi: 10.1063/5.0053409 [13] 郝常乐, 党建军, 陈长盛, 等. 基于双向流固耦合的超空泡射弹入水研究[J]. 力学学报, 2022, 54(3): 678-687. doi: 10.6052/0459-1879-21-510 [14] Kubota A, Kato H, Yamaguchi H. A new modelling of cavitating flows: A numerical study of unsteady cavitation on a hydrofoil section[J]. Journal of fluid Mechanics, 1992, 240: 59-96. doi: 10.1017/S002211209200003X [15] Schnerr G H, Sauer J. Physical and numerical modeling of unsteady cavitation dynamics[C]//Fourth International Conference on Multiphase Flow. New Orleans, LO, USA: ICMF, 2001. -
点击查看大图
计量
- 文章访问数: 79
- HTML全文浏览量: 18
- PDF下载量: 34
- 被引次数: 0
