Error Compensation for Dead Reckoning Based on SVM
-
摘要: 在使用机器学习方法对自主水下航行器(AUV)航位推算进行误差补偿时, 通常采用神经网络算法。但神经网络需要大量的训练样本才能达到稳定的训练结果。为了解决此问题, 文中对支持向量机(SVM)在航位推算的误差补偿问题进行研究。利用SVM训练出误差补偿模型, 对航位推算进行误差补偿, 提高了导航精度。误差补偿模型选取AUV的俯仰角、横滚角和航向角, 多普勒计程仪(DVL)对地的前向、右向和天向速度以及航位推算时间等7个参数作为输入参数, 以全球卫星定位系统(GPS)和惯导+DVL组合提供的经纬度与航位推算的经纬度差作为模型的输出, 训练出误差补偿模型。对比神经网络算法, 在数据量较少的前提下, SVM训练模型和神经网络训练模型的相对误差分别为0.28%和0.93%。进而通过湖上试验得出, SVM训练模型能够将航位推算的相对误差控制在0.5%内。Abstract: In the use of machine learning methods for error compensation in dead reckoning of an autonomous undersea vehicle(AUV), the neural network algorithm is commonly used. However, neural networks require a large number of training samples to achieve stable training results. To solve this problem, research was conducted on the application of support vector machine(SVM) for error compensation in dead reckoning. By utilizing SVM, an error compensation model was trained to correct the errors in dead reckoning, thereby improving navigational accuracy. The error compensation model takes seven parameters as input: pitch angle, roll angle, course angle, forward, right, and upward velocity of the Doppler velocity log(DVL) relative to the ground, and dead reckoning time of the AUV. The difference in latitude and longitude provided by the global positioning system(GPS) and inertial navigation system(INS) + DVL combination compared with latitude and longitude obtained from dead reckoning serves as the output of the model. The SVM trained model and the neural network trained model show a relative error of 0.28% and 0.93%, respectively, when the amount of data is limited. Through lake tests, it is concluded that the model trained by SVM can control the relative error of dead reckoning within 0.5%.
-
表 1 SVM与BP误差补偿效果对比
Table 1. Comparison of error compensation effect between SVM and BP
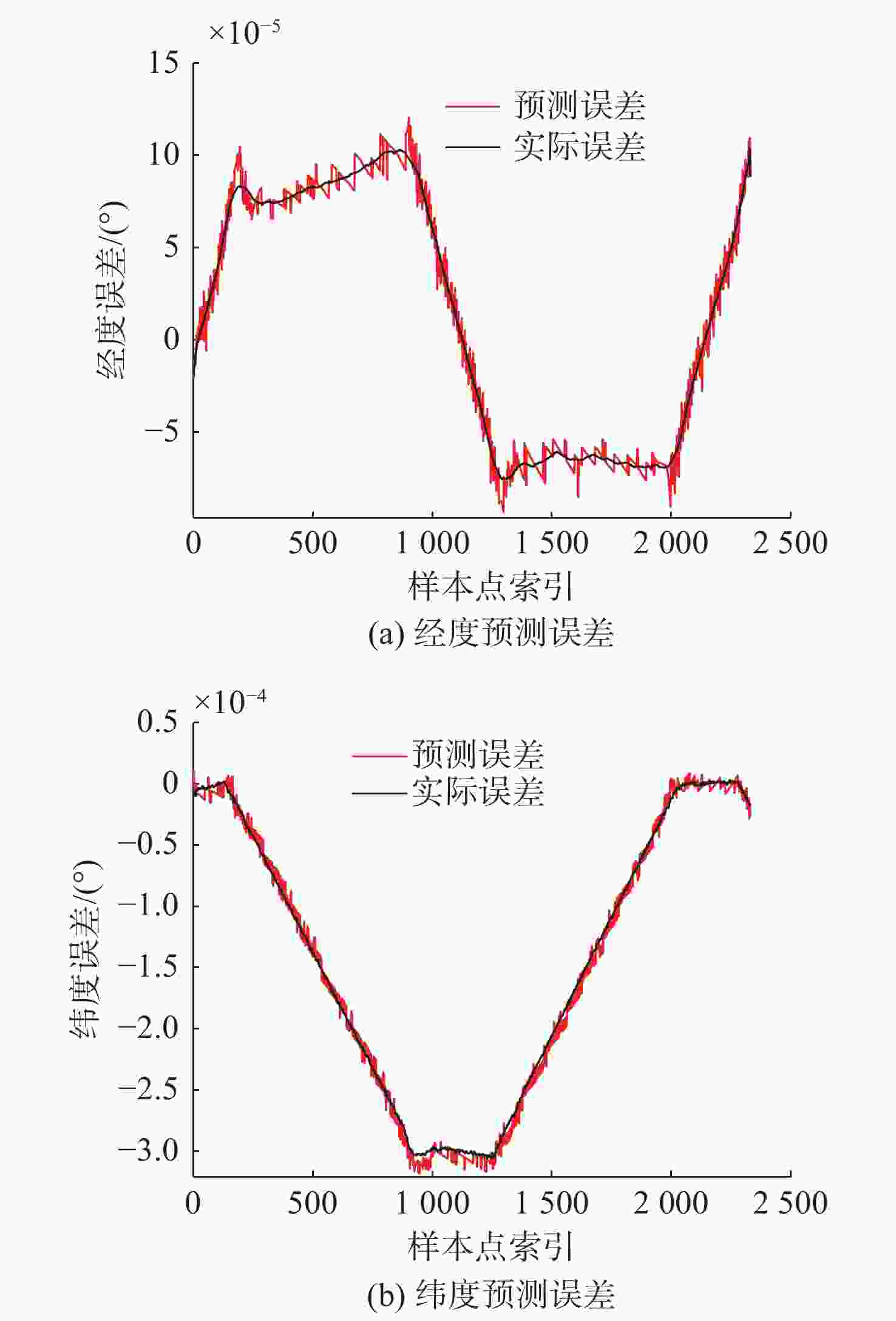
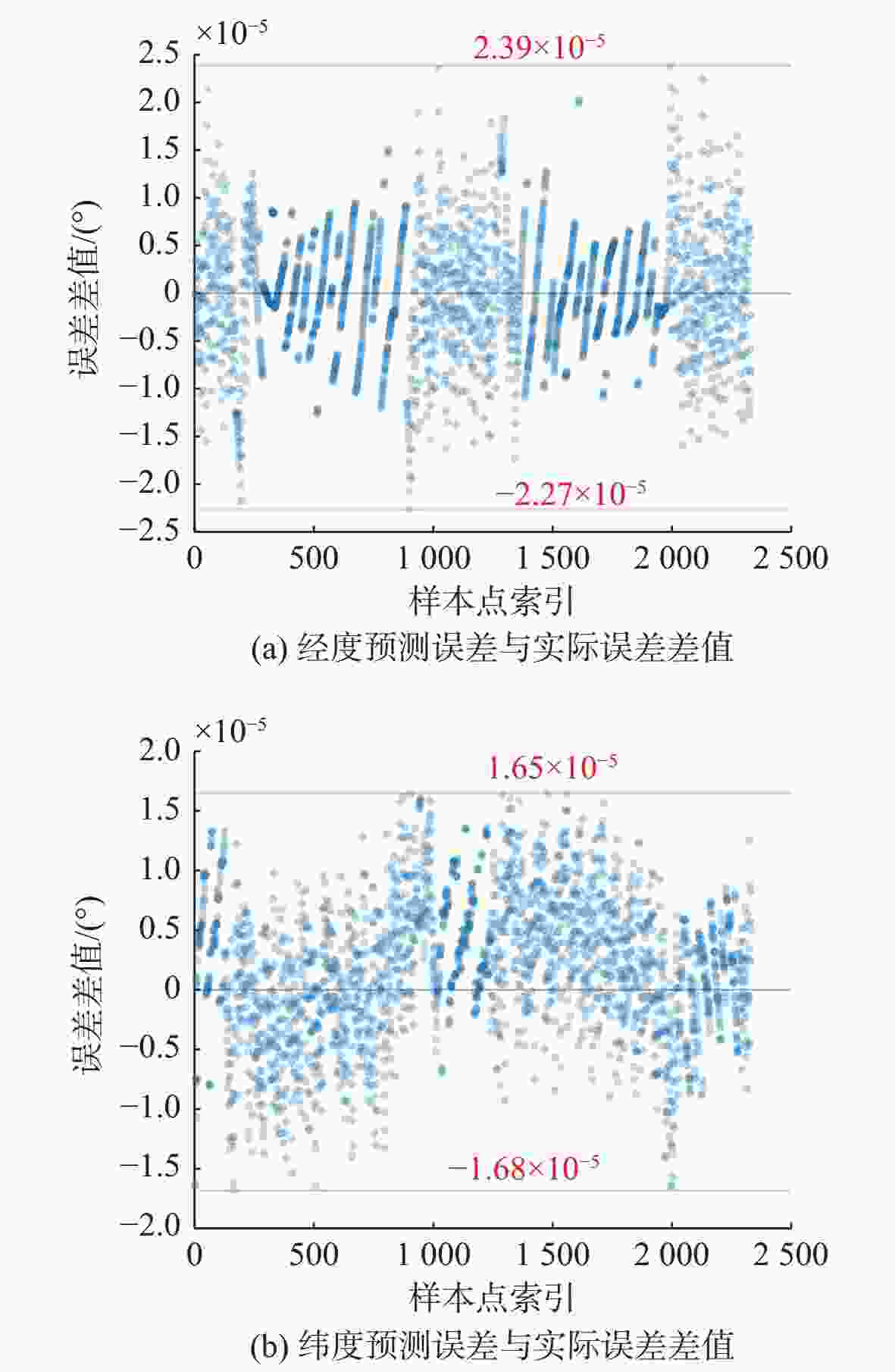
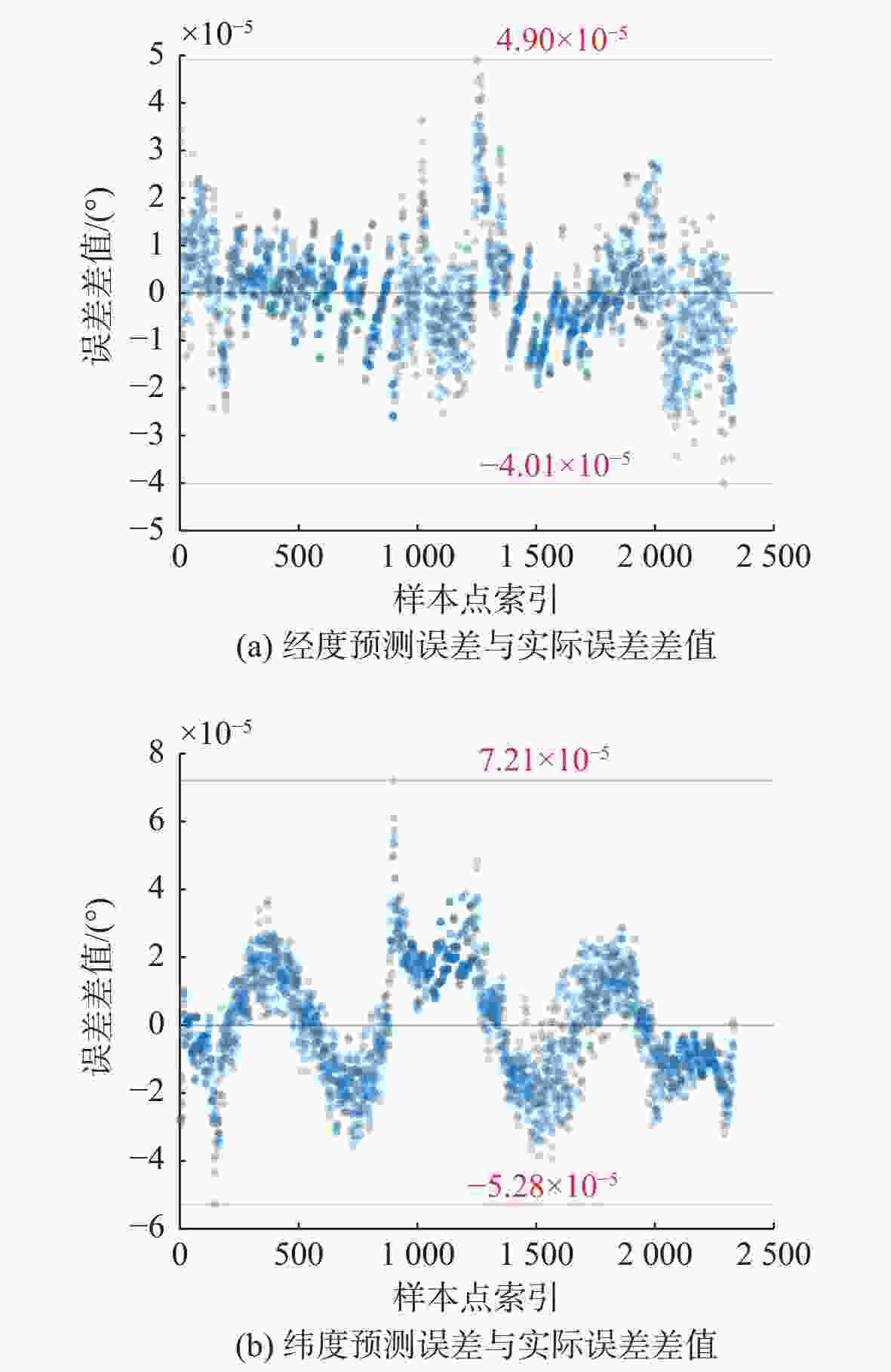
模型 经度误差/(°) 纬度误差/(°) 距离偏差/m 补偿前 1.209×10−4 3.182×10−4 36.447 1 BP 4.904×10−5 7.210×10−5 8.334 4 SVM 2.386×10−5 1.684×10−5 2.489 0 表 2 样本增大前后BP与SVM误差补偿效果对比
Table 2. Comparison of error compensation effect between SVM and BP before and after the sample size increased
模型 经度
误差/(°)纬度
误差/(°)距离
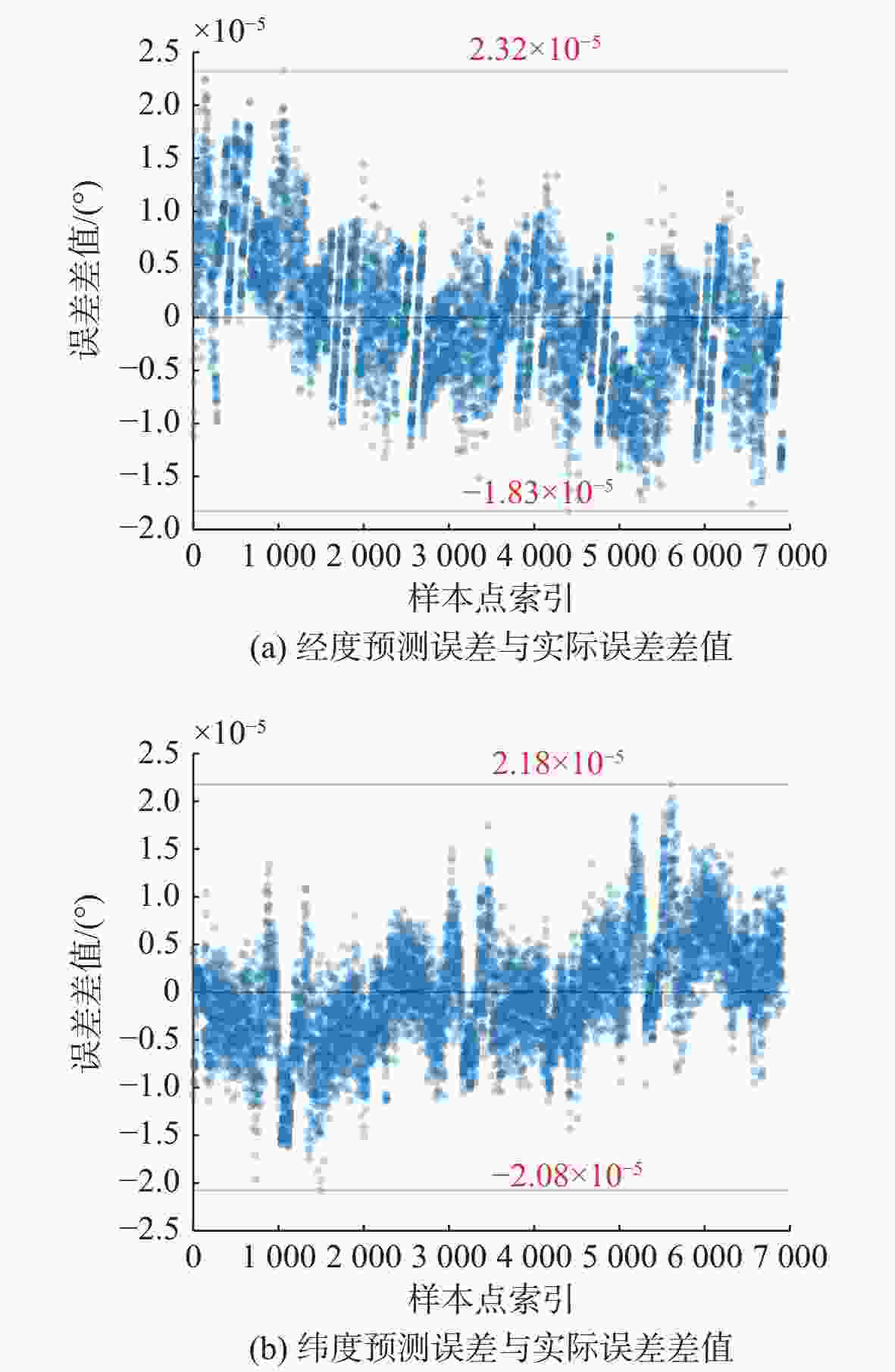
偏差/m样本量/组 SVM 2.386×10−5 1.684×10−5 2.489 0 2 331 BP 4.904×10−5 7.210×10−5 8.334 4 2 331 BP(增) 2.321×10−5 2.176×10−5 2.637 0 6 911 表 3 蛇形轨迹误差补偿前后对比
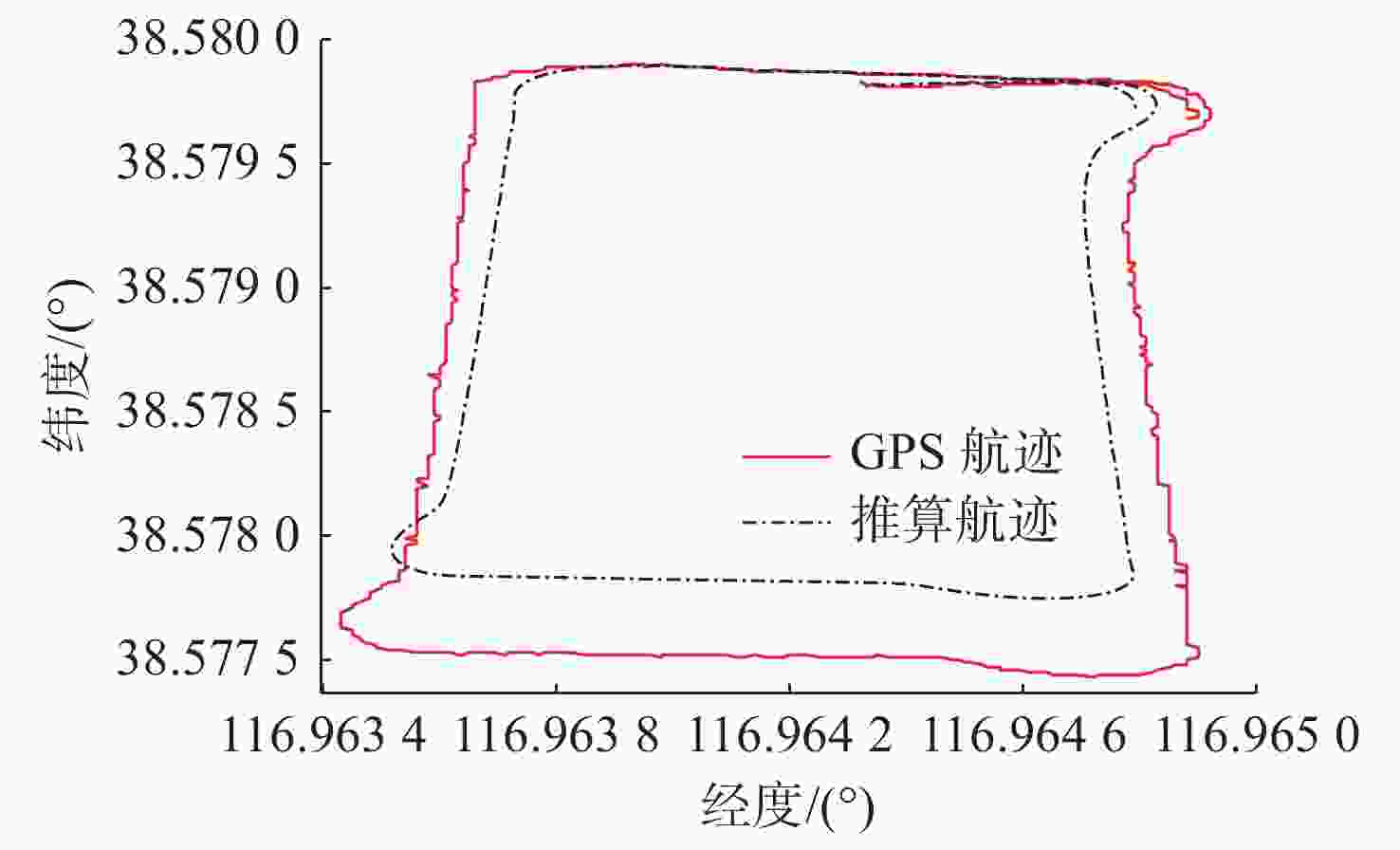
Table 3. Comparison of snake track error before and after compensation
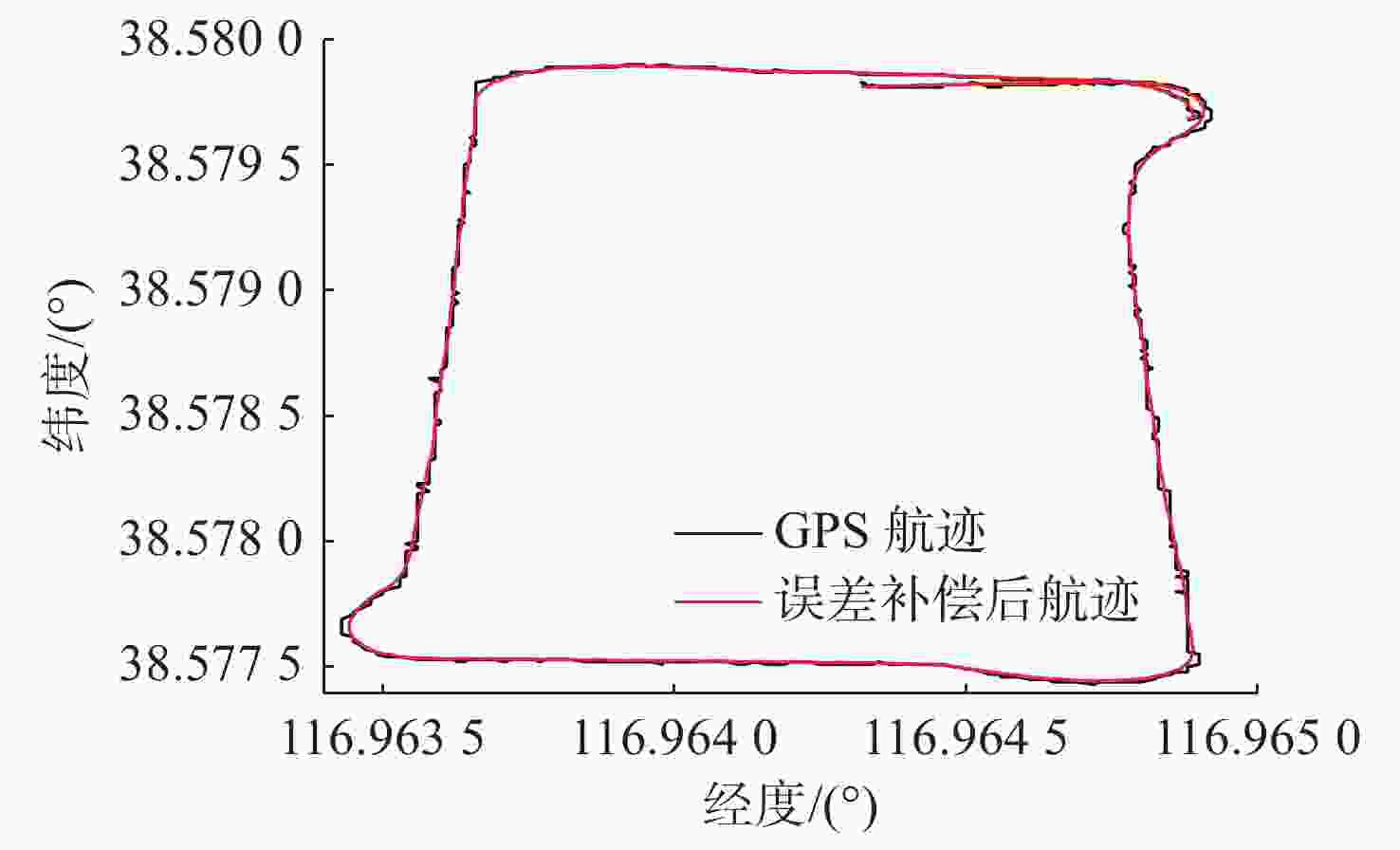
阶段 经度误差/(°) 纬度误差/(°) 距离偏差/m 补偿前 1.179×10−4 3.381×10−4 39.105 补偿后 2.416×10−5 2.086×10−5 2.894 表 4 AUV水下定深试验误差补偿前后对比
Table 4. Comparison of underwater fixed depth experiment errors before and after compensation
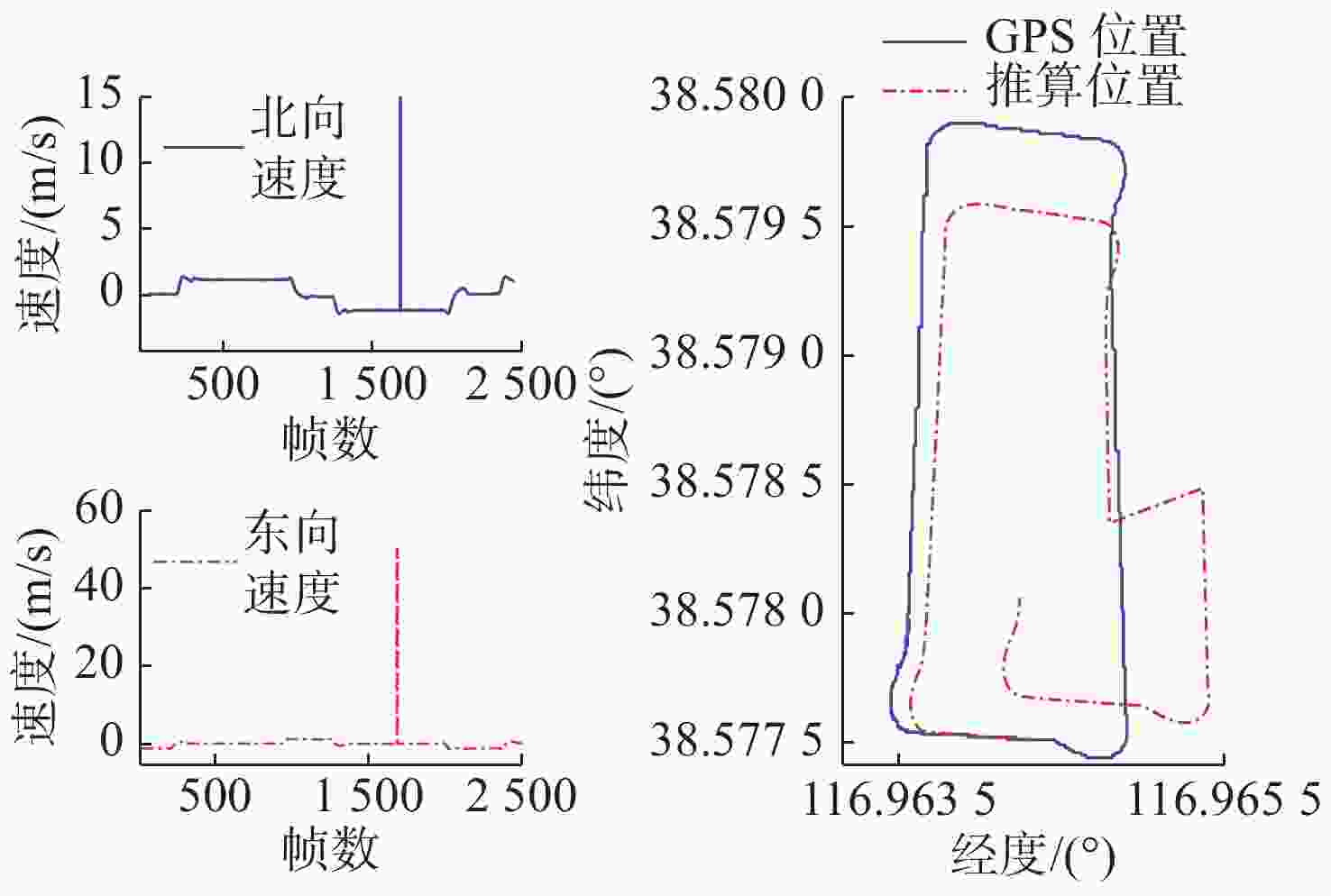
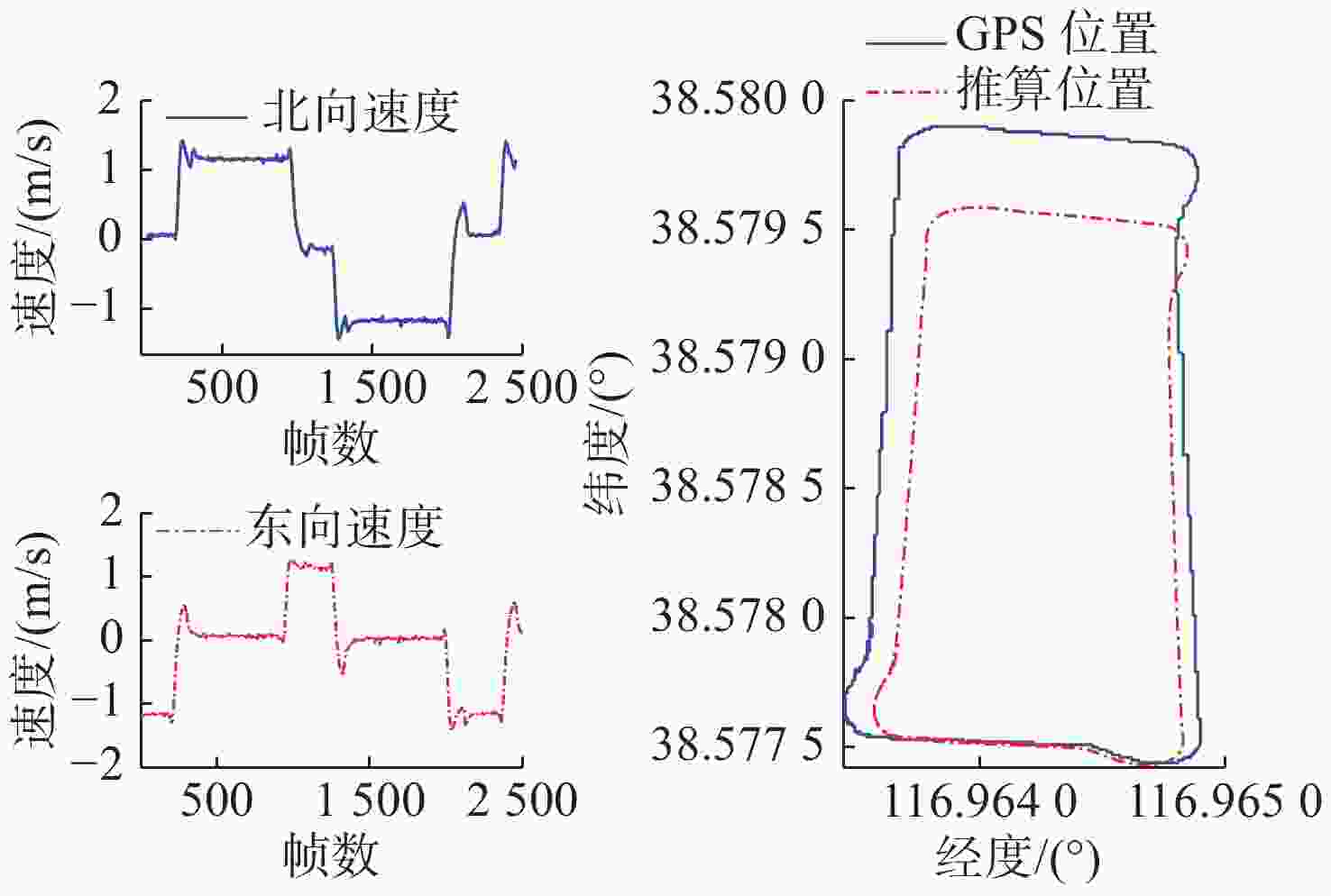
阶段 经度误差/(°) 纬度误差/(°) 距离偏差/m 补偿前 1.126×10−4 2.869×10−4 31.9541 补偿后 9.742×10−5 6.751×10−5 10.2131 表 5 水下定深四边形试验误差补偿前后对比
Table 5. Comparison of underwater depth quadrilateral experiment errors before and after compensation
阶段 经度误差/(°) 纬度误差/(°) 距离偏差/m 补偿前 9.648×10−4 3.486×10−4 38.7740 补偿后 1.542×10−5 2.004×10−5 2.2392 -
[1] MARTINEZ A, HERNANDEZ L, SAHLI H, et al. Model-aided navigation with sea current estimation for an autonomous underwater vehicle[J]. International Journal of Advanced Robotic Systems, 2015, 12(7): 103-116. doi: 10.5772/60415 [2] BARISIC M, MISKOVIC N, VASILIJEVIC A, et al. Fusing hydroacoustic absolute position fixes with AUV on-board dead reckoning[C]//IFAC Symposium on Robot Control. Dubrovnik, Croatia: University of Zagreb, 2012: 211-217. [3] 谢彦新, 胡成全, 王凯, 等. 基于神经网络的航位推算导航[J]. 吉林大学学报(理学版), 2017, 55(5): 1192-1198.XIE Y X, HU C Q, WANG K, et al. Dead-reckoning navigation based on neural network[J]. Journal of Jilin University(Science Edition), 2017, 55(5): 1192-1198. [4] QIU B C, WANG M F, LI H W, et al. Development of hybrid neural network and current forecasting model based dead reckoning method for accurate prediction of underwater glider position[J]. Network Daily News, 2023(4): 59-59. [5] YANG S, SHANG X, SUN T, et al. A new dead reckoning method for HAUVs assisted by a dynamic model with ocean current information[J]. Ocean Engineering, 2024, 295: 116847. doi: 10.1016/j.oceaneng.2024.116847 [6] 岳钰隽, 邱娜, 金志扬, 等. 改进支持向量机的车辆定位导航精度提升方法[J]. 重庆理工大学学报(自然科学), 2023, 37(4): 85-94.YUE Y J, QIU N, JIN Z Y, et al. Research on accuracy improvement of vehicle positioning and navigation with an improved support vector machine[J]. Journal of Chongqing Institute of Technology, 2023, 37(4): 85-94. [7] 彭树萍. AUV 动力学模型辅助的航位推算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2011. [8] 刘桂峰. 水下无人航行器航位推算方法研究[J]. 舰船科学技术, 2021, 43(18): 94-96. doi: 10.3404/j.issn.1672-7649.2021.9A.032LIU G F. Research on dead reckoning method of AUV[J]. Ship Science and Technology, 2021, 43(18): 94-96. doi: 10.3404/j.issn.1672-7649.2021.9A.032 [9] 孙玉山, 代天娇, 赵志平. 水下机器人航位推算导航系统及误差分析[J]. 船舶工程, 2010, 32(5): 67-72. doi: 10.3969/j.issn.1000-6982.2010.05.019SUN Y S, DAI T J, ZHAO Z P. Error analysis of dead-reckoning navigation system for autonomous underwater vehicle[J]. Ship Engineering, 2010, 32(5): 67-72. doi: 10.3969/j.issn.1000-6982.2010.05.019 [10] 吴海波. 基于小波变换的AUV多尺度组合导航算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2017. [11] 李成涛. 不同潜深下水下机器人导航位置修正方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2014. [12] 舒旭光. 基于测速误差预补偿的水下航行体组合导航技术[J]. 现代电子技术, 2014, 37(13): 139-142. doi: 10.3969/j.issn.1004-373X.2014.13.040SHU X G. Integrated navigation technology for underwater vehicles based on precompensation of velocity measurement deviation[J]. Modern Electronics Technique, 2014, 37(13): 139-142. doi: 10.3969/j.issn.1004-373X.2014.13.040 [13] 周博文, 童晖, 张彬, 等. 八波束相控阵换能器的研制[J]. 振动与冲击, 2022, 41(8): 217-222.ZHOU B W, TONG H, ZHANG B, et al. Development of eight-beam phased array transducer[J]. Journal of Vibration and Shock, 2022, 41(8): 217-222. [14] 赵基伟. 基于多传感器融合的微小型AUV导航系统研究[D]. 天津: 河北工业大学, 2022. [15] 崔洪宇, 赵德有, 王锋. 海洋平台灰预测和支持向量机的逆控制[J]. 哈尔滨工程大学学报, 2009, 30(6): 613-618. doi: 10.3969/j.issn.1006-7043.2009.06.004CUI H Y, ZHAO D Y, WANG F. Adaptive inverse control of offshore platform vibrations using grey forecasting and a support vector machine[J]. Journal of Harbin Engineering University, 2009, 30(6): 613-618. doi: 10.3969/j.issn.1006-7043.2009.06.004 [16] 罗康, 崔海英. 螺旋桨转速信息辅助水下航行器组合导航研究[J]. 计算机仿真, 2013, 30(12): 302-305, 320. doi: 10.3969/j.issn.1006-9348.2013.12.071LUO K, CUI H Y. Research on integrated navigation technology assisted by propeller speed information for AUV[J]. Computer Simulation, 2013, 30(12): 302-305, 320. doi: 10.3969/j.issn.1006-9348.2013.12.071 -




 下载:
下载: