Theories and Experiments of Torpedo Shaped Charge Warhead Penetration into Water-partitioned Armor
-
摘要: 为了合理预测鱼雷聚能战斗部对含水复合装甲的侵彻威力, 基于A-T模型和两阶段孔径增长理论, 并结合基于虚拟原点理论的侵彻体侵彻过程分析, 提出了对含水复合装甲侵彻深度和穿孔直径的理论模型。开展了缩比鱼雷聚能战斗部侵彻含水复合装甲试验研究, 其中鱼雷头段分别采用单层铝板和累计一定厚度的间隔铝板模拟, 同步开展侵彻威力数值仿真。对理论计算、仿真和试验结果进行了对比分析, 验证了理论模型的合理性。相关研究可以为鱼雷聚能战斗部威力快速预测、优化设计以及针对潜艇防护结构尺寸及参数特性的大威力新型聚能战斗部技术研究提供支撑。Abstract: To reasonably predict the penetration power of a torpedo shaped charge warhead into water-partitioned armor, a theoretical model for calculating the generated penetration depth and aperture diameters was proposed based on the A-T model and the two-step mechanism of aperture growth in combination with the penetrator penetration process analysis based on the virtual origin theory. The experiments and simulations for a reduced-scale torpedo shaped charge warhead penetration into water-partitioned armor targets were conducted, in which a single-layer aluminum plate and the spaced aluminum plates with a certain cumulative thickness were used to simulate the torpedo heads. Calculations, simulations, and experimental results were then compared and analyzed, which verified the rationality of the theoretical model. The research can provide support for the penetration power prediction and the optimization design of torpedo shaped charge warheads, as well as the technical research of new powerful torpedo shaped charge warheads to more effectively destroy the submarine protective structure.
-
Key words:
- torpedo /
- shaped charge warhead /
- water-partitioned armor /
- theoretical calculation /
- penetration power
-
图 1 射流两阶段孔径增长受力示意图
Figure 1. Force analysis diagram of the two-step mechanism of aperture growth in jet flow
图 3 缩比鱼雷聚能战斗部及药型罩实物照片
Figure 3. Photograph of the scaling torpedo shaped charge warhead and the liner
图 7 聚能侵彻体成型参数选取
Figure 7. Selection of the forming parameters of the shaped charge penetrator
图 8 缩比鱼雷聚能战斗部侵彻含水复合装甲仿真结果
Figure 8. Simulation results of the scaling torpedo shaped charge warhead into water-partitioned armor
图 10 聚能侵彻体在侵彻路径上的速度变化理论计算和数值仿真对比
Figure 10. Comparisons between the calculations and simulations of the velocity variation of the shaped charge penetrator on the penetration path
表 1 6种材料模型参数
Table 1. Model parameters of the six materials
DNAN基高能炸药 紫铜 2A12铝 45钢 水 空气 参数 数值 参数 数值 参数 数值 参数 数值 参数 数值 参数 数值 ρ/(g/cm3) 1.73 ρ/(g/cm3) 8.96 ρ/(g/cm3) 2.77 ρ/(g/cm3) 7.89 ρ/(g/cm3) 1 C0 0 D/(m/s) 7980 G/GPa 46 G/GPa 25.9 G/GPa 77 γ 0.28 C1 10−5 P/GPa 29.7 A/GPa 0.09 A/GPa 0.265 A/GPa 0.507 C/(m/s) 1 483 C2 0 A/GPa 588.3 B/GPa 0.292 B/GPa 0.426 B/GPa 0.32 Si 1.75 C3 0 B/GPa 12.9 n 0.31 n 0.34 n 0.28 C4 0.4 R1 4.38 C 0.025 C 0.015 C 0.064 C5 0.4 R2 1.2 m 1.09 m 1 m 1.06 C6 0 ω 0.36 Tm/K 1356 Tm/K 775 Tm/K 1 795 Tr/K 300 Tr/K 294 Tr/K 298 
下载: 导出CSV
表 2 聚能侵彻体成型参数
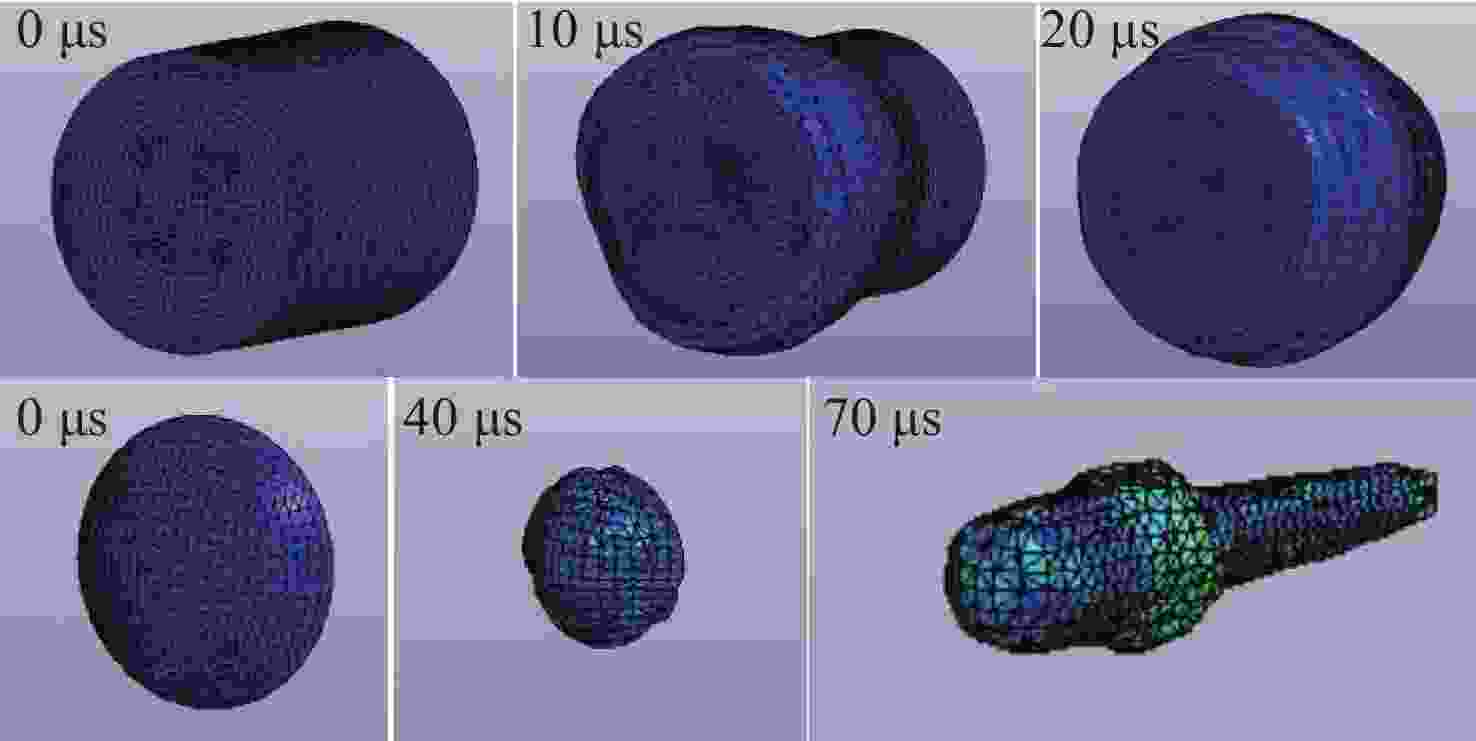
Table 2. The forming parameters of the shaped charge penetrator
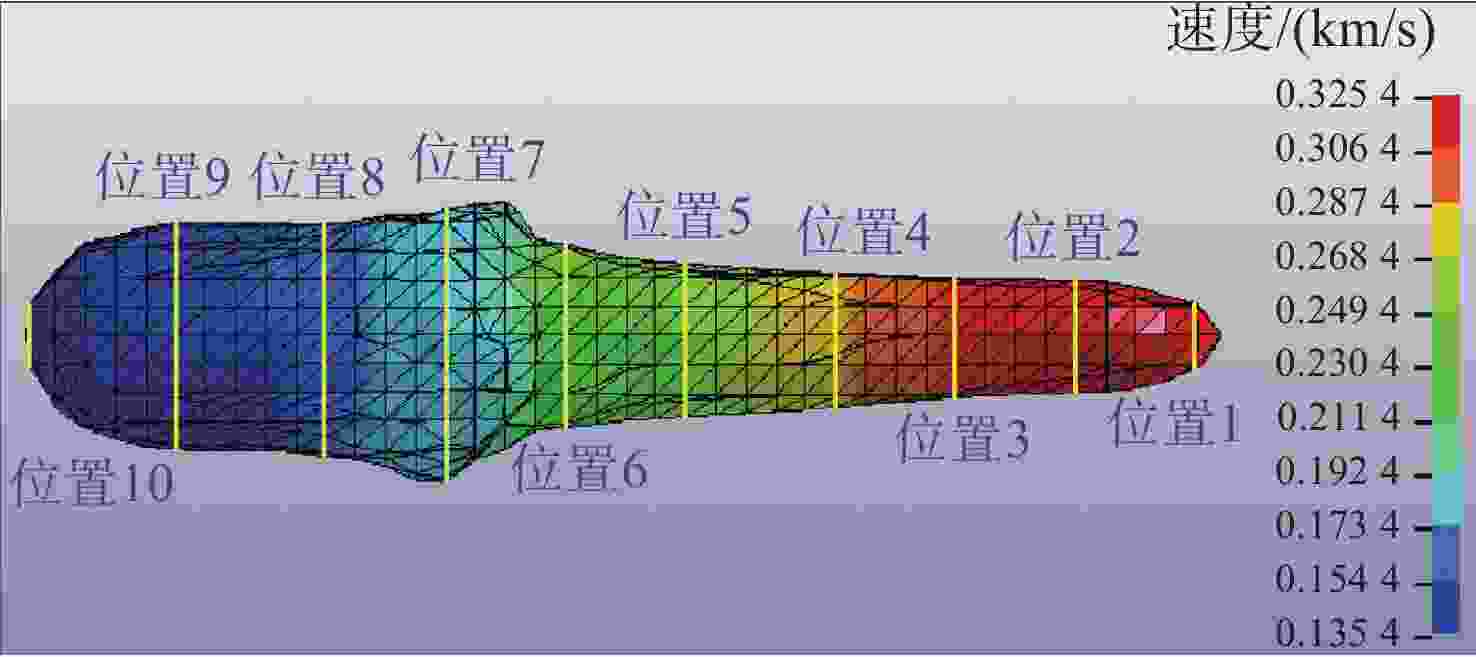
位置 距坐标原点距离/(mm) 速度/(m/s) 直径/(mm) 1 280.2 3 254 6.49 2 267.9 3 245 10.91 3 256.0 3 108 11.83 4 244.3 2 894 13.10 5 229.6 2 608 15.00 6 217.9 2 350 18.15 7 206.2 1 985 26.72 8 194.3 1 573 23.02 9 179.7 1 358 22.17 10 165.1 1 354 6.21
下载: 导出CSV
表 3 理论计算、仿真与试验结果对比
Table 3. Comparison of results of the calculation, simulation and the experiment
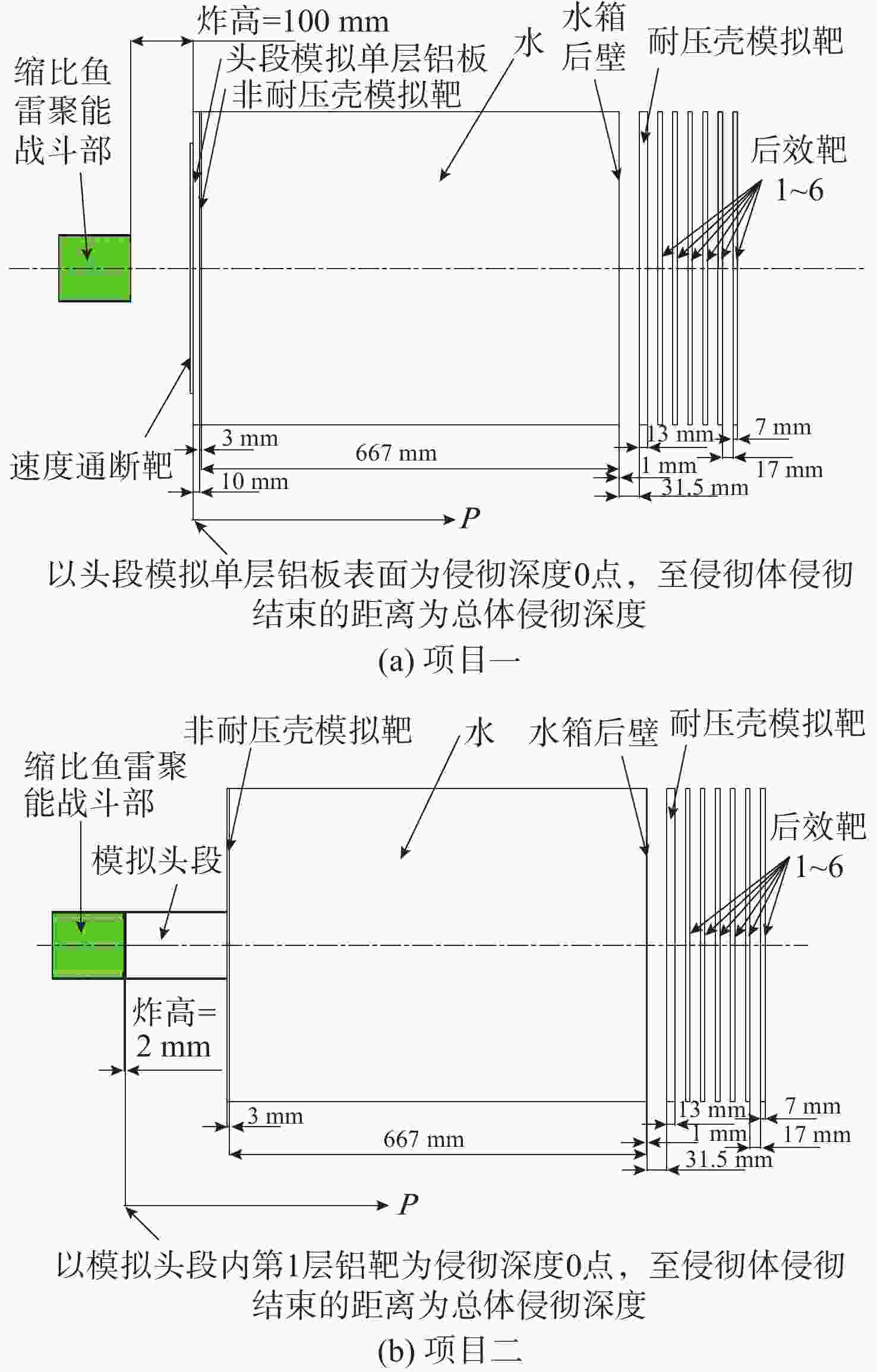
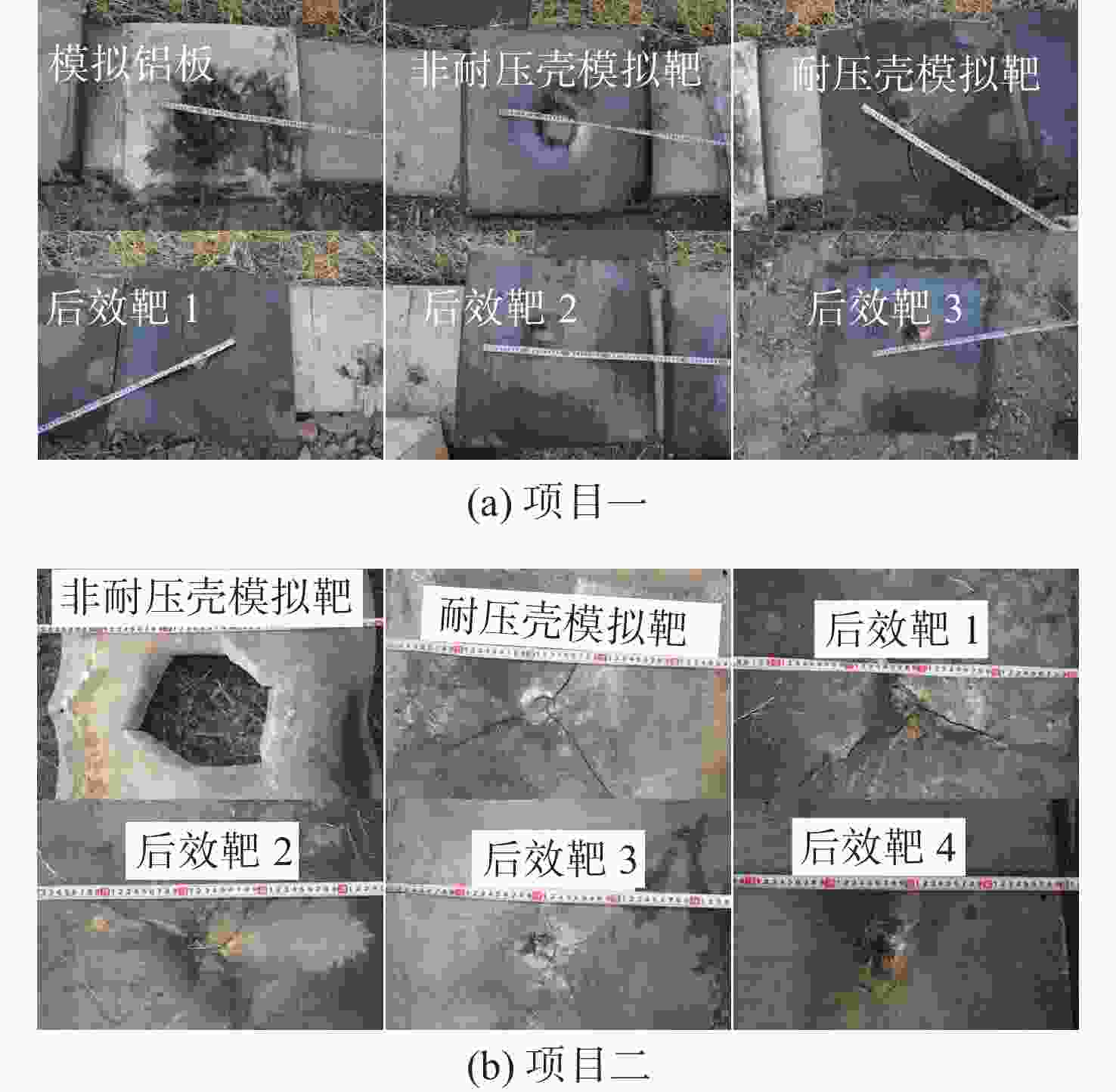
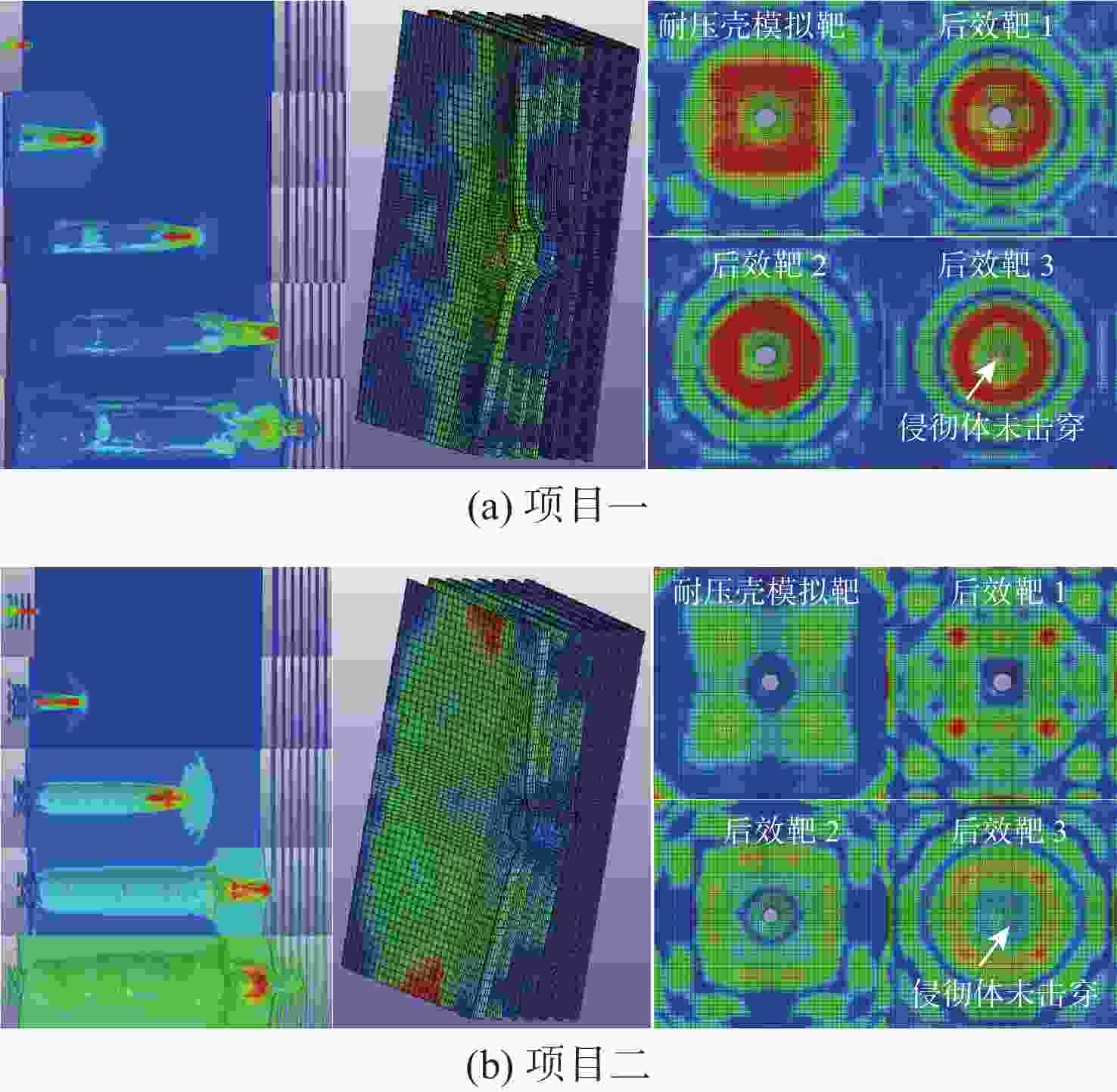
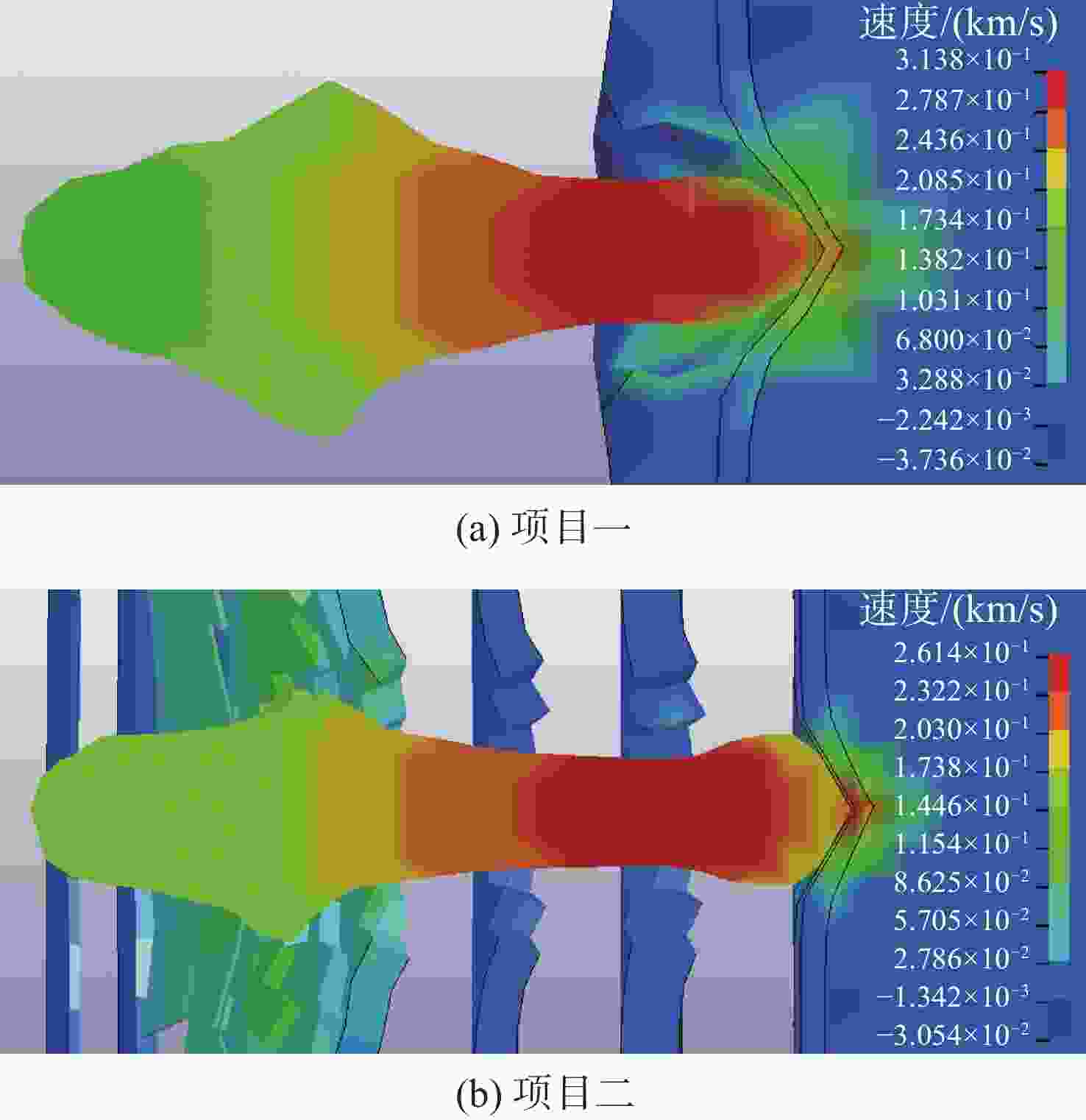
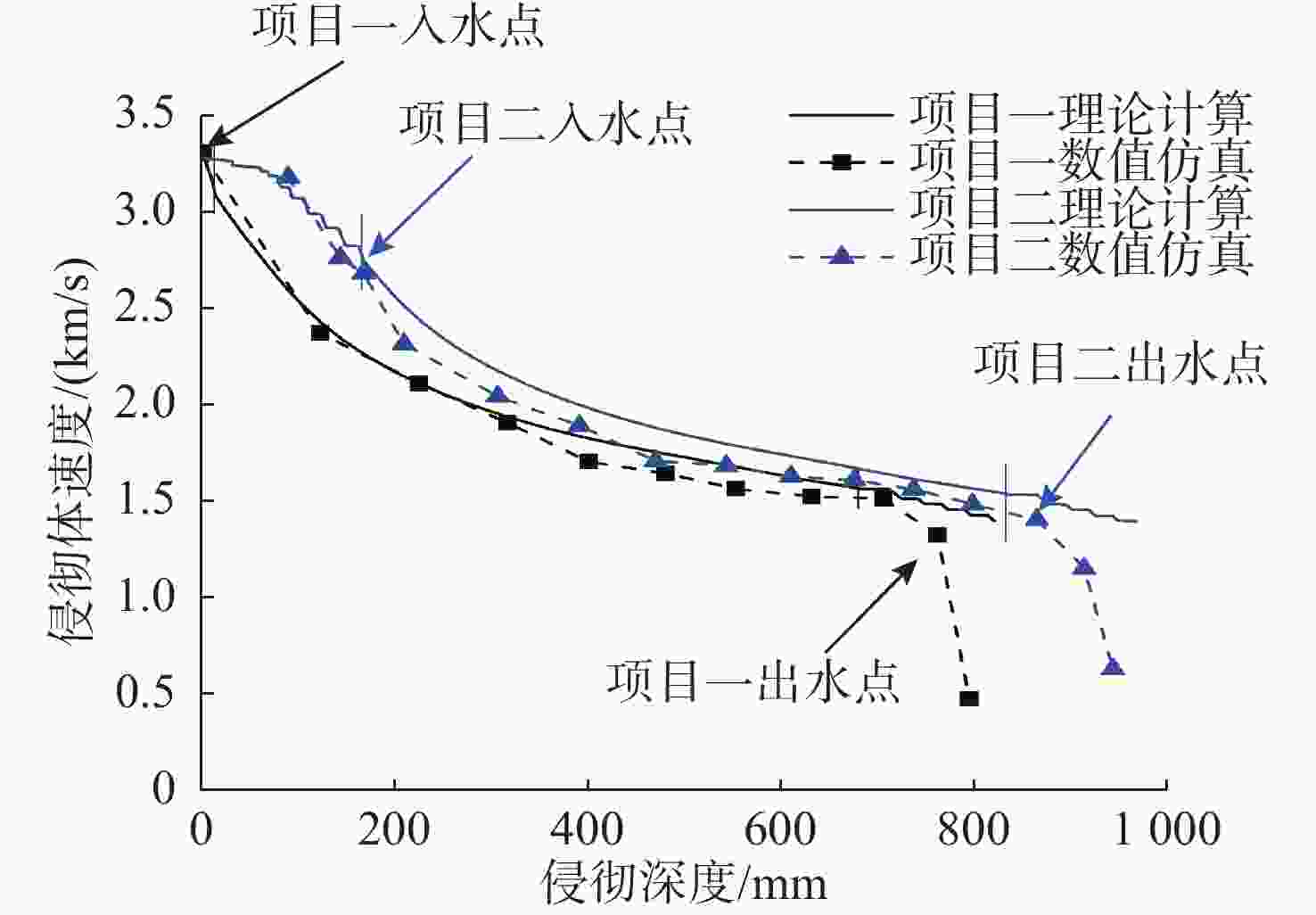
项目 方法 耐压壳模拟靶孔径/mm 后效靶1孔径/mm 后效靶2孔径/mm 后效靶3孔径/mm 总体侵彻深度/mm 项目一 试验 ϕ41.3 ϕ62.3 ϕ58.7 ϕ39.9 814 计算 ϕ36.2(12.4%) ϕ35.9(42.4%) ϕ35.6(39.4%) ϕ35.2(11.8%) 822(1.0%) 仿真 ϕ44.5(7.7%) ϕ54.3(12.8%) ϕ50.4(14.1%) — 797(2.1%) 项目二 试验 ϕ27.3 ϕ35.3 ϕ29.6 ϕ32.3 976 计算 ϕ30.0(9.9%) ϕ29.7(15.9%) ϕ29.4(0.7%) ϕ29.1(9.9%) 969(0.7%) 仿真 ϕ32.1(17.6%) ϕ40.1(13.6%) ϕ34.3(15.9%) — 947(3.0%)
下载: 导出CSV
-
[1] 蒋文灿, 程祥珍, 梁斌, 等. 一种组合药型罩聚能装药战斗部对含水复合结构毁伤的数值模拟及试验研究[J]. 爆炸与冲击, 2022, 42(8): 1-15.JIANG W C, CHENG X Z, LIANG B, et al. Numerical simulation and experimental study on the damage of water partitioned structure by a shaped charge warhead with a combined charge liner[J]. Explosion and Shock Waves, 2022, 42(8): 1-15. [2] 李海龙, 王博, 丁松, 等. 冲击波和侵彻体联合作用下聚脲涂层防护机理研究[J]. 水下无人系统学报, 2022, 30(3): 354-363. doi: 10.11993/j.issn.2096-3920.2022.03.011LI H L, WANG B, DING S, et al. Study on the protection mechanisms of a polyurea coating subjected to shock waves and penetrators[J]. Journal of Unmanned Undersea Systems, 2022, 30(3): 354-363. doi: 10.11993/j.issn.2096-3920.2022.03.011 [3] 鲁忠宝, 李军林, 鲁海玲, 等. 耦合爆炸式鱼雷战斗部研究现状与展望[J]. 水下无人系统学报, 2022, 30(3): 314-320. doi: 10.11993/j.issn.2096-3920.2022.03.006LU Z B, LI J L, LU H L, et al. Research status and prospects for coupling explosion-based torpedo warheads[J]. Journal of Unmanned Undersea Systems, 2022, 30(3): 314-320. doi: 10.11993/j.issn.2096-3920.2022.03.006 [4] 王长利, 周刚, 马坤, 等. 典型含水复合结构在聚能装药水下爆炸作用下的毁伤[J]. 船舶力学, 2018, 22(8): 1001-1010. doi: 10.3969/j.issn.1007-7294.2018.08.010WANG C L, ZHOU G, MA K, et al. Damage analysis of typical water partitioned structure under shaped charge underwater explosion[J]. Journal of Ship Mechanics, 2018, 22(8): 1001-1010. doi: 10.3969/j.issn.1007-7294.2018.08.010 [5] 杨贵涛, 俞旸晖, 张红, 等. 钽合金EFP对含水复合装甲毁伤仿真与试验[J]. 水下无人系统学报, 2022, 30(3): 332-337. doi: 10.11993/j.issn.2096-3920.2022.03.008YANG G T, YU Y H, ZHANG H, et al. Simulations and experiments on the damage of tantalum alloy EFP to water-partitioned armor[J]. Journal of Unmanned Undersea Systems, 2022, 30(3): 332-337. doi: 10.11993/j.issn.2096-3920.2022.03.008 [6] 李兵, 刘念念, 陈高杰, 等. 水中聚能战斗部毁伤双层圆柱壳的数值模拟与试验研究[J]. 兵工学报, 2018, 39(1): 38-45. doi: 10.3969/j.issn.1000-1093.2018.01.004LI B, LIU N N, CHEN G J, et al. Numerical simulation and experimental research on damage of shaped charge warhead to double-layer columniform shell[J]. Acta Armamentarii, 2018, 39(1): 38-45. doi: 10.3969/j.issn.1000-1093.2018.01.004 [7] BIRKHOFF G, MACDOUGALL D P, PUGH E M, et al. Explosives with lined cavities[J]. Journal of Applied Physics, 1948, 19(6): 563-582. doi: 10.1063/1.1698173 [8] ALEKSEEVSKII V P. Penetration of a rod into a target at high velocity[J]. Combustion Explosion and Shock Waves, 1966, 2(2): 63-66. [9] TATE A. A theory for the deceleration of long rods after impact[J]. Journal of the Mechanics & Physics of Solids, 1967, 15(6): 387-399. [10] TATE A. Further results in the theory of long rod penetration[J]. Journal of the Mechanics & Physics of Solids, 1969, 17(3): 141-150. [11] XIAO Q Q, HUANG Z X, ZU X D, et al. Influence of drift velocity and distance between jet particles on the penetration depth of shaped charges[J]. Propellants, Explosives, Pyrotechnics, 2016, 41(1): 76-83. doi: 10.1002/prep.201500051 [12] ZHU Q F, HUANG Z X, XIAO Q Q, et al. Theoretical considerations on cavity diameters and penetration depths of concrete materials generated by shaped charge jets using the targets response modes described by a modified HJC model[J]. International Journal of Impact Engineering, 2020, 138: 103439. doi: 10.1016/j.ijimpeng.2019.103439 [13] SZENDREI T. Analytical model of crater formation by jet impact and its application to calculation of penetration curves and hole profiles[C]//7th International Symposium on Ballistics. The Hague, Netherlands: International Ballistics Committee, 1983. [14] HELD M, HUANG N S, JIANG D, et al. Determination of the crater radius as a function of time of a shaped charge jet that penetrates water[J]. Propellants Explosives Pyrotechnics, 2010, 21(2): 64-69. [15] HILL R. Cavitation and the influence of headshape in attack of thick targets by non-deforming projectiles[J]. Journal of the Mechanics & Physics of Solids, 1980, 28(5-6): 249-263 [16] MILLER C W. Two-dimensional engineering model of jet penetration[C]//15th International Symposium on Ballistics. Israel: International Ballistics Committee, 1995. [17] LEE M. Cavitation and mushrooming in attack of thick targets by deforming rods[J]. Journal of Applied Mechanics, 2001, 68(3): 420-424. doi: 10.1115/1.1360690 [18] ALLISON F E, VITALI R. A new method of computing penetration variables for shaped charge jets[R]. MD, USA: Army Ballistic Research Lab Aberdeen Proving Ground, No. BRL-1184, 1963. [19] CHOU P C, CARLEONE J. The breakup of shaped charge jets[C]//2nd International Symposium on Ballistics. Daytona Beach, FL: International Ballistics Committee, 1976. [20] PREFFER G. Determination par simulations numeiques do l'stat et des lois de fragmentation des jets de charges creuses[C]//5th International Symposium on Ballistics, Toulouse, France: International Ballistics Committee, 1980. [21] HIRSCH E. A formula for the shaped charge jet breakup-time[J]. Propellants, Explosives, Pyrotechnics, 1979, 4(5): 89-94. [22] PACK D C. On the perturbation and break up of a high-speed, elongating metal jet[J]. Journal of Applied Physics, 1988, 63(6): 1864-1871. doi: 10.1063/1.339883 [23] ROMERO L A. The instability of rapidly stretching plastic jets[J]. Journal of Applied Physics, 1989, 65(8): 6-16. [24] FRANKEL I, WEIHS D. Stability of a capillary jet with linearly increasing axial velocity(with application to shaped charges)[J]. Journal of Fluid Mechanics, 2006, 155(155): 289-307. [25] 郑哲敏. 聚能射流的稳定性问题[J]. 爆炸与冲击, 1981(1): 6-17.ZHENG Z M. Stability of jet produced by shaped charge[J]. Explosion and Shock Waves, 1981(1): 6-17. [26] ROSENBERG Z, DEKEL E. The penetration of rigid long rods-revisited[J]. International Journal of Impact Engineering, 2009, 36(4): 551-564. doi: 10.1016/j.ijimpeng.2008.06.001 -
点击查看大图
图(10) / 表(3)
计量
- 文章访问数: 96
- HTML全文浏览量: 67
- PDF下载量: 10
- 被引次数: 0
