Finding Probability of Submarine-Launched Acoustic Homing Torpedoes Based on Gaussian Process Regression
-
摘要: 明确潜射声自导鱼雷的发现概率, 对相关战术制定具有显著作用。传统解析算法和统计算法无法平衡概率评估的快速性和精确性, 针对此问题, 文中提出了一种基于高斯过程回归的发现概率评估模型, 以及基于解析模型的训练数据集生成方法, 并在特定态势下开展了发现概率评估的数值仿真。结果显示, 文中所提方法具有很好的评估效果, 可为相关战场决策提供理论支撑。Abstract: The determination of the finding probability of submarine-launched acoustic homing torpedoes significantly affects tactical formulation. Conventional analytical and statistical algorithms fail to balance the speed and precision of probability assessment. In response to this issue, this paper introduced a model for assessing the finding probability based on Gaussian process regression. Additionally, a method was proposed for generating a training dataset based on the analytical model. Numerical simulations for assessing the finding probability were conducted within a specific battlefield scenario. The outcomes illustrate the superior assessment effect of the proposed method, offering theoretical support for decision-making in relevant battlefield contexts.
-
图 1 初始雷目距离3 km处脱靶量采样值
Figure 1. The sampling values of miss distance at 3 km initial distance between torpedo and target
图 2 声自导鱼雷一次转角弹道水平面示意图
Figure 2. Diagram of trajectory of acoustic homing torpedo with one time rotating in horizonal plane
图 3 声自导鱼雷捕获目标极限情况态势
Figure 3. Diagram of limitary battlefield situation when acoustic homing torpedo finds target
图 8 发现概率预测与验证相对误差
Figure 8. Relative errors of prediction and validation of finding probability
表 1 战场态势参数设置
Table 1. Parameters setting of battlefield situation
名称 参数 初始雷目距离/km 10/5/50 初始目标舷角/(°) 0/10/180 鱼雷速度/kn 50 声自导探测距离/m 1 500 声自导探测扇面半角/(°) 50 鱼雷初始段航程/m 500 鱼雷回转半径/m 50 鱼雷初始发射提前角/(°) 20 目标速度/kn 20 目标航向/(°) 180 鱼雷速度误差标准差/kn 3 鱼雷航向误差标准差/(°) 1 探测目标速度误差标准差/kn 3 探测目标航向误差标准差/(°) 1 目标速度误差标准差/kn 3 目标航向误差标准差/(°) 1 目标初始方位探测误差标准差/(°) 1 目标初始距离探测误差标准差/m 1%初始距离 
下载: 导出CSV
表 2 不同核函数均方根误差
Table 2. RMSE of different kernel functions
高斯核函数 RMSE RQK 0.010 640 SEK 0.011 284 MK5/2 0.010 881 EK 0.012 799
下载: 导出CSV
表 3 需预测发现概率的新态势条件
Table 3. New situation for which the finding probability is needed to be predicted
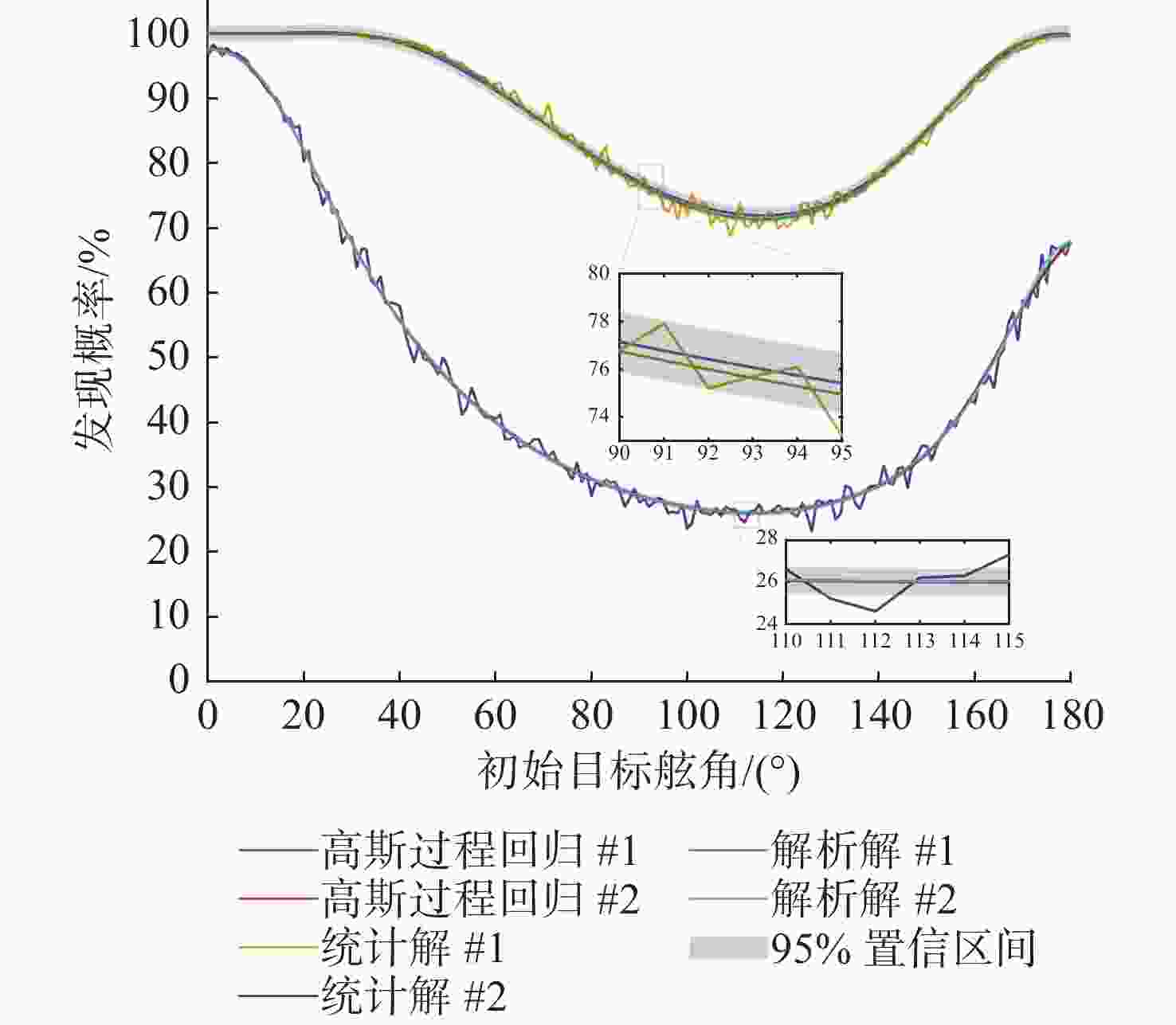
编号 初始雷目距离/m 初始目标舷角/(°) 1 12 345 0~180(间隔1°) 2 34 567 0~180(间隔1°)
下载: 导出CSV
表 4 预测和验证相对误差范围及态势占比
Table 4. Relative error range of prediction and validation and percentage of battlefield situation
类别 相对误差范围/% 态势占比/% 预测 0~1 97.24 0~2 100 验证 0~3 79.83 0~5 93.92
下载: 导出CSV
-
[1] 孟庆玉, 张静远, 宋保维. 鱼雷作战效能分析[M]. 北京: 国防工业出版社, 2003. [2] 杨绪升, 刘建兵, 周庆飞. 声自导鱼雷射击诸元及误差对其捕获概率的影响[J]. 指挥控制与仿真, 2009, 31(5): 93-97. doi: 10.3969/j.issn.1673-3819.2009.05.024 [3] 薄玉成. 武器系统设计理论[M]. 北京: 北京理工大学出版社, 2010. [4] 谢超, 周景军, 万亚民, 等. 基于脱靶量散布的超空泡鱼雷命中概率研究[J]. 水下无人系统学报, 2022, 30(2): 237-244, 253. doi: 10.11993/j.issn.2096-3920.2022.02.015Xie Chao, Zhou Jingjun, Wan Yamin, et al. Research on hitting probability of supercavitating torpedo based on dispersion of miss distance[J]. Journal of Unmanned Undersea Systems, 2022, 30(2): 237-244, 253. doi: 10.11993/j.issn.2096-3920.2022.02.015 [5] 谢超, 周景军, 万亚民, 等. 超空泡鱼雷命中概率解析方法[J]. 水下无人系统学报, 2022, 30(5): 656-664. doi: 10.11993/j.issn.2096-3920.202111002Xie Chao, Zhou Jingjun, Wan Yamin, et al. Analytical method for hitting probability of supercavitating torpedo[J]. Journal of Unmanned Undersea Systems, 2022, 30(5): 656-664. doi: 10.11993/j.issn.2096-3920.202111002 [6] 李勐, 代志恒. 直航鱼雷发现概率的解析计算方法[J]. 指挥控制与仿真, 2007, 39(4): 55-59. [7] 武志东, 于雪泳, 许兆鹏. 潜射鱼雷命中概率的解析计算通式及应用[J]. 水下无人系统学报, 2021, 29(2): 203-209.Wu Zhidong, Yu Xueyong, Xu Zhaopeng. Analytic formula and employment of the hitting probability for sub-launched torpedo[J]. Journal of Unmanned Undersea Systems, 2021, 29(2): 203-209. [8] 胡星志, 王旭, 江雄, 等. 基于高斯过程回归的高超声速飞行器不确定轨迹预测[J]. 空天技术, 2022(4): 49-61. [9] Quinonero-Candela J, Rasmussen C E. A unifying view of sparse approximate Gaussian process regression[J]. The Journal of Machine Learning Research, 2005, 6: 1939-1959. [10] Schulz E, Speekenbrink M, Krause A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions[J]. Journal of Mathematical Psychology, 2018, 85: 1-16. doi: 10.1016/j.jmp.2018.03.001 -
点击查看大图
计量
- 文章访问数: 116
- HTML全文浏览量: 56
- PDF下载量: 28
- 被引次数: 0
