目标运动要素解算质量评价体系构建与评估

张洪瑞; 李斌; 程帅; 寇小明

doi:10.11993/j.issn.2096-3920.2023-0109

目标运动要素解算质量评价体系构建与评估

doi: 10.11993/j.issn.2096-3920.2023-0109

中国船舶集团有限公司第七〇五研究所, 陕西西安, 710077

详细信息

作者简介:
张洪瑞(1999-), 男, 在读硕士, 主要研究方向为声自导总体技术

中图分类号: TJ634; U674
计量
- 文章访问数: 65
- HTML全文浏览量: 18
- PDF下载量: 27
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-21
- 修回日期: 2024-01-30
- 录用日期: 2024-02-07
- 网络出版日期: 2024-08-05

Construction and Assessment of Quality Evaluation System for Solving Target Motion Elements

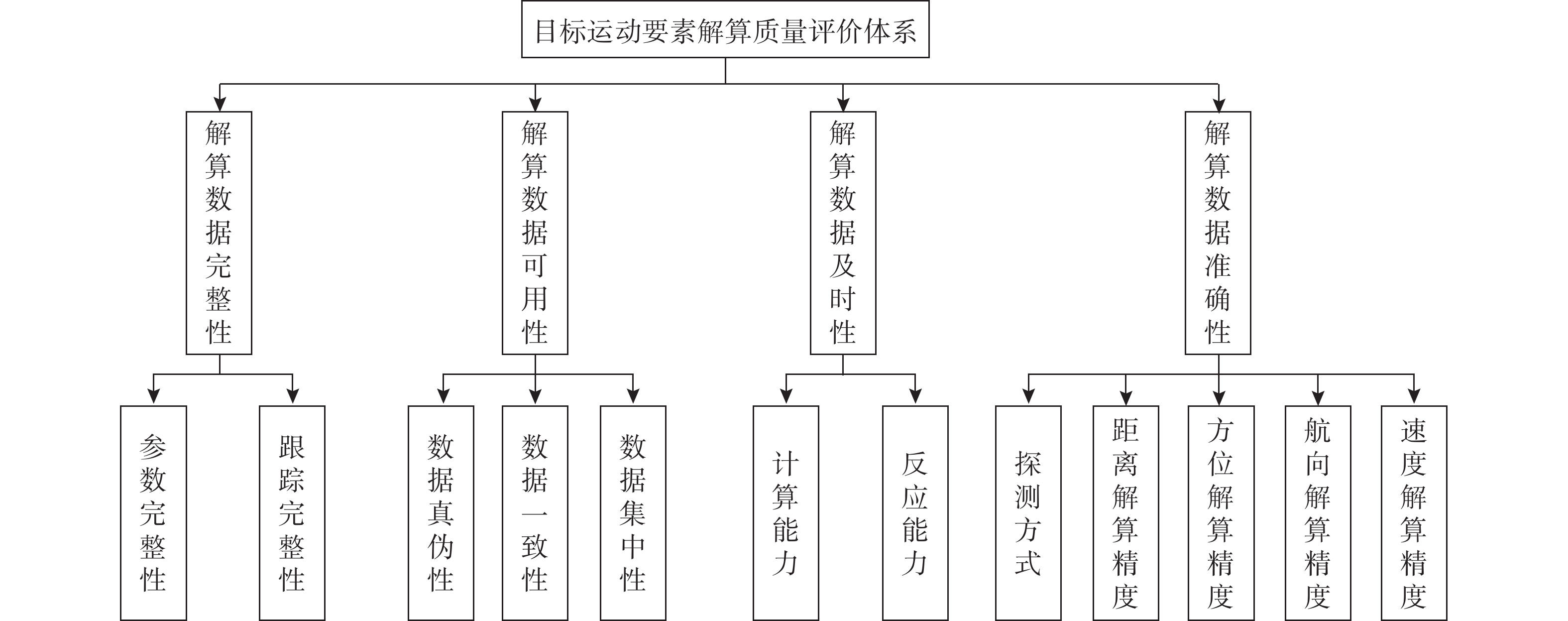
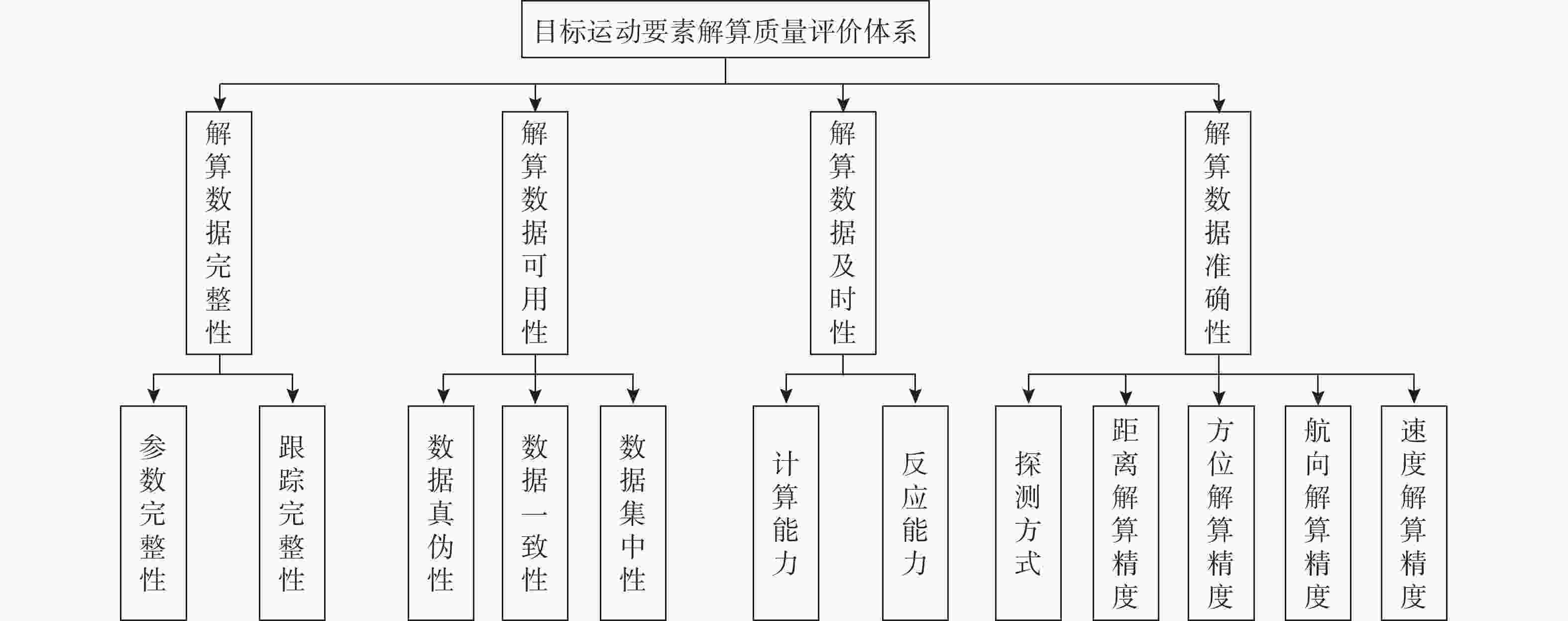
The 705 Research Institute, China State Shipbuilding Corporation Limited, Xi’an 710077, China

摘要

摘要: 水面舰艇反潜作战过程中, 目标跟踪是其重要组成部分。目标跟踪过程中通过目标运动要素解算得到目标四要素信息, 并通过解算结果计算命中概率。目标运动要素的解算结果受战场情况、探测方式以及解算模型等多方面因素影响, 为将各个分离的单一因素关联起来, 文中从解算数据完整性、可用性、及时性以及准确性4个方面构建了一种目标运动要素解算质量评价体系, 以总偏差最小为目的将层次分析法和熵权法有效结合以确定指标权重, 经加权求和得到目标运动要素解算质量评估值, 并与命中概率仿真结果进行对比分析。仿真结果表明, 使用解算质量计算出的近似命中概率与实际命中概率误差小于9.2%, 文中构建的评价体系能有效将各个信息结合起来, 合理充分地表达命中概率, 有利于交战决策。
- 目标跟踪 /
- 目标运动要素 /
- 质量评价 /
- 层次分析法 /
- 熵权法
Abstract: Target tracking is an important part of the anti-submarine warfare process of surface ships. In the process of target tracking, the four elements of targets are obtained through the target motion element solving, and the hit probability is calculated through the result. The solution results of the target motion elements are affected by many factors, such as battlefield situation, detection method, and solution model. In order to associate the separated factor, a quality evaluation system for solving target motion elements was constructed from the four aspects of completeness, availability, timeliness, and accuracy of the solved data. In order to minimize the total deviation, the analytic hierarchy method and entropy weight method were effectively combined to determine the index weight. The quality evaluation value of the target motion elements was obtained by weighted summation and compared with the simulation result of hit probability. The simulation results show that the error between the approximate hit probability and the actual hit probability calculated by using the solved mass is less than 9.2%. The evaluation system constructed in this paper can effectively combine all information, reasonably and fully express the hit probability, and is conducive to the decision-making of the engagement.
- target tracking /
- target motion elements /
- quality evaluation /
- analytic hierarchy process /
- entropy weight method

HTML全文

图 1 目标运动要素解算质量评价体系

Figure 1. Quality evaluation system of target motion elements calculation

下载: 全尺寸图片幻灯片

图 2 近似命中概率与命中概率对比图

Figure 2. Comparison of approximate hit probability and hit probability

下载: 全尺寸图片幻灯片

表 1 数据真伪性等级

Table 1. Levels of data authenticity

可信度	等级	可信度	等级
完全不可信	1	基本可信	3
基本不可信	2	完全可信	4

下载: 导出CSV

表 2 计算能力等级

Table 2. Levels of calculate ability

解算时间/ms	等级	解算时间/ms	等级
≥5 800	1	≥800	5
≥4 000	2	≥500	6
≥2 700	3	<500	7
≥1 500	4

下载: 导出CSV

表 3 反应能力等级

Table 3. Levels of reaction ability

反应周期	等级	反应周期	等级
≥12	1	≥5	4
≥9	2	≥3	5
≥6	3	<3	6

下载: 导出CSV

表 4 探测方式等级

Table 4. Levels of detection method

探测方式	等级
被动声呐探测	1
主动声呐探测	2
主被动声呐联合探测	3

下载: 导出CSV

表 5 距离解算等级

Table 5. Levels of Distance Calculation

距离解算误差	等级	距离解算误差	等级
≥15.3%D	1	≥1.1%D	5
≥10.8%D	2	≥0.8%D	6
≥7.2%D	3	<0.8%D	7
≥3.6%D	4

下载: 导出CSV

表 6 速度解算等级

Table 6. Levels of velocity calculation

速度解算误差/kn	等级	速度解算误差/kn	等级
≥8	1	≥2	5
≥5.8	2	≥1.4	6
≥3.9	3	<1.4	7
≥2.8	4

下载: 导出CSV

表 7 航向解算等级

Table 7. Levels of course calculation

航向解算误差/(°)	等级	航向解算误差/(°)	等级
≥50	1	≥4	4
≥25	2	<4	5
≥10	3

下载: 导出CSV

表 8 方位解算等级

Table 8. Levels of bearing calculation

方位解算误差/(°)	等级	方位解算误差/(°)	等级
≥7.8	1	≥1.3	4
≥4.6	2	<1.3	5
≥2.5	3

下载: 导出CSV

表 9 AHP法元素含义

Table 9. Element meaning in AHP method

${a_{ij}}$值	含义
1	因素i和j具有同样的重要程度
3	因素i比j略微重要
5	因素i比j较重要
7	因素i比j非常重要
9	因素i比j极为重要
2, 4, 6, 8	介于2个相邻判断尺度中间

下载: 导出CSV

表 10 随机一致性指标表

Table 10. Stochastic consistency index

N	1	2	3	4	5
$RI$	0	0	0.58	0.90	1.12

N	6	7	8	9	10
$RI$	1.24	1.32	1.41	1.45	1.49

下载: 导出CSV

表 11 一级评价指标判断矩阵、一致性检验结果和判别权重表

Table 11. Judgement matrix, consistency test results and discriminant weights for level 1 evaluation indicators

判断矩阵	一致性检验结果	判别权重
${\boldsymbol{A}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} 1&2&3&{1/4} \\ {1/2}&1&2&{1/3} \\ {1/3}&{1/2}&1&{1/5} \\ 4&3&5&1 \end{array}} \right]$	0.039 1	$ \boldsymbol{w} = (0.22,0.15,0.08,0.55) $

下载: 导出CSV

表 12 二级评价指标判断矩阵、一致性检验结果和判别权重表

Table 12. Judgement matrix, consistency test results and discriminant weights for level 2 evaluation indicators

判断矩阵	一致性检验结果	判别权重
$ {{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} 1&3 \\ {1/3}&1 \end{array}} \right] $	0	$ {\boldsymbol{w}_1} = (0.75,0.25) $
$ {{\boldsymbol{A}}_2}{\text{ = }}\left[ {\begin{array}{*{20}{c}} 1&2&3 \\ {1/2}&1&2 \\ {1/3}&{1/2}&1 \end{array}} \right] $	0.004 6	$ {\boldsymbol{w}_2} = (0.54,0.30,0.16) $
${{\boldsymbol{A}}_3} = \left[ {\begin{array}{*{20}{c}} 1&3 \\ {1/3}&1 \end{array}} \right]$	0	$ {\boldsymbol{w}_3} = (0.75,0.25) $
$ {{\boldsymbol{A}}_4} = \left[ {\begin{array}{*{20}{c}} 1&{1/3}&1&2&2 \\ 3&1&3&5&4 \\ 1&{1/3}&1&3&2 \\ {1/2}&{1/5}&{1/3}&1&{1/2} \\ {1/2}&{1/4}&{1/2}&2&1 \end{array}} \right] $	0.016 7	$ {\boldsymbol{w}_4} = (0.17,0.47,0.18,0.07,0.11) $

下载: 导出CSV

表 13 AHP法各指标权重

Table 13. The weight of each index of AHP method

指标	权重	指标	权重
参数完整性	0.1650	反应能力	0.0200
跟踪完整性	0.0550	探测方式	0.0935
数据真伪性	0.0810	距离解算精度	0.2585
数据一致性	0.0450	方位解算精度	0.0990
数据集中性	0.0240	航向解算精度	0.0605
计算能力	0.0600	速度解算精度	0.0385

下载: 导出CSV

表 14 距离解算等级归一化

Table 14. Distance solver level normalisation

距离解算误差	距离解算等级	距离解算等级归一化
$ \geqslant15.3\text{%}D $	$ 1 $	0
$ \geqslant10.8\text{%}D $	$ 2 $	$ 1/6 $
$ \geqslant7.2\text{%}D $	$ 3 $	$ 1/3 $
$ \geqslant3.6\%D $	$ 4 $	$ 1/2 $
$ \geqslant1.1\text{%}D $	$ 5 $	$ 2/3 $
$ \geqslant0.8\text{%}D $	$ 6 $	$ 5/6 $
$ < 0.8\text{%}D $	$ 7 $	$ 1 $

下载: 导出CSV

表 15 仿真实验数据

Table 15. Data from simulation experiments

周期	计算能力	反应能力	距离解算精度	方位解算精度	航向解算精度	速度解算精度
2	1704.7	8	3.08	1.83	19.20	6.94
3	1059.9	8	2.61	1.64	9.13	4.38
4	929.3	7	2.55	1.55	6.17	3.34
5	925.3	7	2.47	1.50	4.40	2.65
6	875.2	8	2.43	1.48	3.32	2.16
7	870.0	6	2.33	1.46	2.67	1.76
8	890.5	5	2.25	1.45	2.17	1.45
9	868.6	4	2.17	1.45	1.87	1.22
10	871.7	4	2.12	1.44	1.62	1.07
11	867.2	3	2.08	1.44	1.38	0.96
12	833.9	3	1.94	1.43	1.19	0.82
13	862.0	3	1.89	1.43	1.07	0.73
14	862.7	2	1.85	1.42	0.97	0.66
15	867.7	2	1.84	1.42	0.88	0.59

下载: 导出CSV

表 16 熵权法各指标权重

Table 16. The weight of each index in the entropy weight method

指标	熵值	权重
计算能力	0.723 5	0.218 9
反应能力	0.659 8	0.269 3
距离解算精度	0.848 8	0.119 7
方位解算精度	0.848 8	0.172 3
航向解算精度	0.780 4	0.046 0
速度解算精度	0.782 3	0.173 8

下载: 导出CSV

表 17 近似命中概率与命中概率对比表

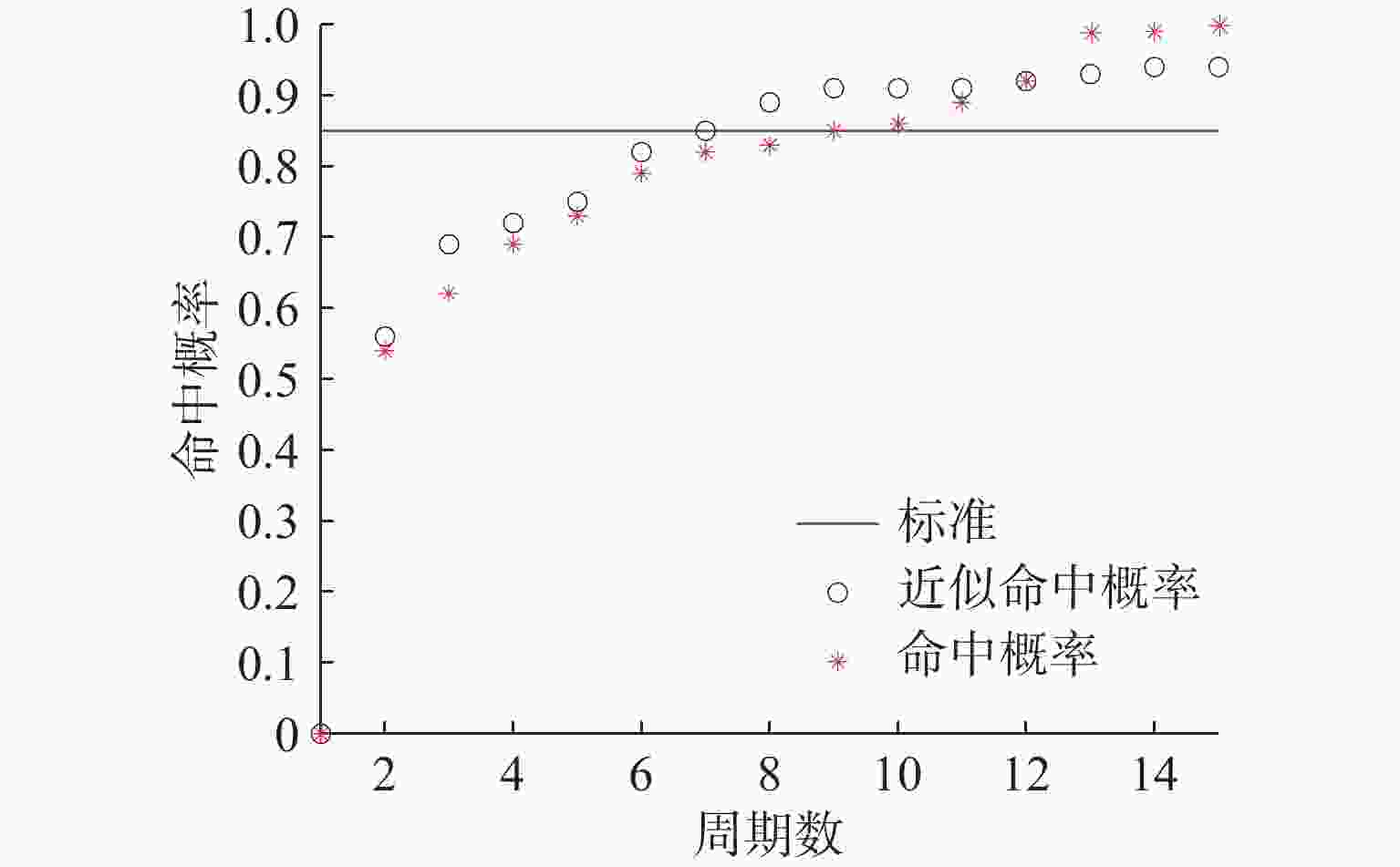
Table 17. Table of approximate hit probability and hit probability

周期	P	P′	周期	P	P′
2	0.54	0.56	8	0.83	0.89
3	0.62	0.69	9	0.85	0.91
4	0.69	0.72	10	0.86	0.91
5	0.73	0.75	11	0.89	0.91
6	0.79	0.82	12	0.92	0.92
7	0.82	0.85	13	0.99	0.93

下载: 导出CSV

表 18 解算质量得分评价表

Table 18. Score evaluation of solution quality

得分	评价	得分	评价
≥0.91	准确命中	≥0.56	基本不会命中
≥0.82	基本命中	<0.56	不会命中
≥0.72	不一定命中

下载: 导出CSV

表 19 不同工况下仿真结果对比表

Table 19. Comparison table of simulation results under different working conditions

工况	周期	$ P' $	评价	P	误差/%
1	3	0.58	基本不会命中	0.56	3.5
	6	0.72	不一定命中	0.72	0
	9	0.88	基本命中	0.83	6.0
2	3	0.60	基本不会命中	0.55	9.1
	6	0.77	不一定命中	0.81	4.9
	9	0.92	准确命中	0.86	6.9
3	3	0.68	基本不会命中	0.64	6.3
	6	0.82	基本命中	0.79	3.8
	9	0.95	准确命中	0.88	7.9

下载: 导出CSV

参考文献(16)

[1]	ABDELPAKEY M H, SHEHATA M S. NullSpaceRDAR: Regularized discriminative adaptive nullspace for object tracking[J]. Image and Vision Computing, 2022, 127: 61-69.
[2]	金杨. 基于深度学习的机动目标Kalman滤波跟踪算法[D]. 贵阳: 贵州师范大学, 2022.
[3]	梁斌, 高阳, 史晓春. 潜艇与水下无人航行器协同反潜作战运用方法[J]. 舰船科学技术, 2022, 44(10): 102-106. doi: 10.3404/j.issn.1672-7649.2022.10.020 LIANG B, GAO Y, SHI X C. Research on collaborative application method of submarine and unmanned underwater vehicle in anti-submarine warfare[J]. Ship Science and Technology, 2022, 44(10): 102-106. doi: 10.3404/j.issn.1672-7649.2022.10.020
[4]	张安民. 纯方位目标运动分析与鱼雷智能导引律研究[D]. 西安: 西北工业大学, 2002.
[5]	侯宝娥, 闫雪. 水面舰艇反鱼雷武器系统作战试验要素分析[J]. 舰船电子工程, 2020, 40(4): 13-15, 33. doi: 10.3969/j.issn.1672-9730.2020.04.004 HOU B E, YAN X. Analysis of operational test elements for shipborne anti-torpedo weapon system[J]. Ship Electronic Engineering, 2020, 40(4): 13-15, 33. doi: 10.3969/j.issn.1672-9730.2020.04.004
[6]	王凯帅, 孙健, 刘冠杉. 本艇机动对鱼雷武器系统攻击效能的影响分析[J]. 数字海洋与水下攻防, 2018, 1(2): 11-15. WANG K S, SUN J, LIU G S. Influence analysis of submarine maneuvering on attack effectiveness of torpedo weapon system[J]. Digital Ocean and Underwater Warfare, 2018, 1(2): 11-15.
[7]	袁富宇, 代志恒, 肖碧琴. 单平台纯方位信息的水面编队目标运动要素解算[J]. 火力与指挥控制, 2021, 46(12): 141-148. doi: 10.3969/j.issn.1002-0640.2021.12.022 YUAN F Y, DAI Z H, XIAO B Q. Calculation of target movement elements of the surface shipformation based on bearing-only information from a single platform[J]. Fire Control and Command Control, 2021, 46(12): 141-148. doi: 10.3969/j.issn.1002-0640.2021.12.022
[8]	程善政, 陈双, 何心怡. 一种目标运动要素纯方位解算方法[J]. 舰船科学技术, 2020, 42(23): 129-132. doi: 10.3404/j.issn.1672-7649.2020.12.025 CHENG S Z, CHEN S, HE X Y. A movement parameters calculating method base on bearings-only[J]. Ship Science and Technology, 2020, 42(23): 129-132. doi: 10.3404/j.issn.1672-7649.2020.12.025
[9]	杨槐, 宫研生. 作战数据在指挥决策中的作用评估方法研究[J]. 兵工自动化, 2012, 31(6): 25-27, 34. doi: 10.3969/j.issn.1006-1576.2012.06.008 YANG H, GONG Y S. Research on assessment methods of role of combat data in command and decision-making[J]. Ordnance Industry Automation, 2012, 31(6): 25-27, 34. doi: 10.3969/j.issn.1006-1576.2012.06.008
[10]	刘立军. 作战数据质量模型构建与质量评估[J]. 火炮发射与控制学报, 2017, 38(3): 37-41. LIU L J. Operational data quality model and quality evaluation[J]. Journal of Gun Launch & Control, 2017, 38(3): 37-41.
[11]	张文明, 薛青. 粗糙集方法在作战仿真数据挖掘中的应用[J]. 系统仿真学报, 2006(S2): 179-181. doi: 10.3969/j.issn.1004-731X.2006.z2.053 ZHANG W M, XUE Q. Application of rough set in date mining of warfare simulation[J]. Journal of System Simulation, 2006(S2): 179-181. doi: 10.3969/j.issn.1004-731X.2006.z2.053
[12]	韩志军, 李锰, 孙少斌. 大型仿真推演系统数据质量评估方法[J]. 火力与指挥控制, 2016, 41(1): 77-80, 84. doi: 10.3969/j.issn.1002-0640.2016.01.018 HAN Z J, LI M, SUN S B. Data quality evaluating method of large-scale simulation rehearsal system[J]. Fire Control and Command Control, 2016, 41(1): 77-80, 84. doi: 10.3969/j.issn.1002-0640.2016.01.018
[13]	杨丽娟, 田铮, 赵伟, 等. 基于变权模型的鱼雷综合性能评估方法[J]. 鱼雷技术, 2014, 22(3): 221-225. YANG L J, TIAN Z, ZHAO W, et al. A method of comprehensive performance evaluation for torpedo based on variable weight model[J]. Torpedo Technology, 2014, 22(3): 221-225.
[14]	王兴隆, 陈仔燕, 刘岩. 基于组合赋权法的空管监视信息质量评估[J]. 中国安全科学学报, 2022, 32(1): 41-50. WANG X L, CHEN Z Y, LIU Y. Quality assessment of air traffic control surveillance information based on combined empowerment approach[J]. China Safety Science Journal, 2022, 32(1): 41-50.
[15]	宋保维, 李楠, 毛昭勇. 模糊层次分析法在鱼雷作战效能评估中的应用[J]. 鱼雷技术, 2010, 18(4): 249-252. SONG B W, LI N, MAO Z Y. Application of FAHP to torpedo operational effectiveness evaluation[J]. Torpedo Technology, 2010, 18(4): 249-252.
[16]	褚双磊, 魏志强, 任强, 等. 基于AHP-熵权法的民用飞机运行需求模糊综合评价[J]. 上海工程技术大学学报, 2021, 35(4): 362-369. CHU S L, WEI Z Q, REN Q, et al. Fuzzy comprehensive evaluation of civil aircraft operational requirement based on AHP-entropy method[J]. Journal of Shanghai University of Engineering Science, 2021, 35(4): 362-369.