Development Characteristics of Underwater Detonation Gas Jets in Confined Space
-
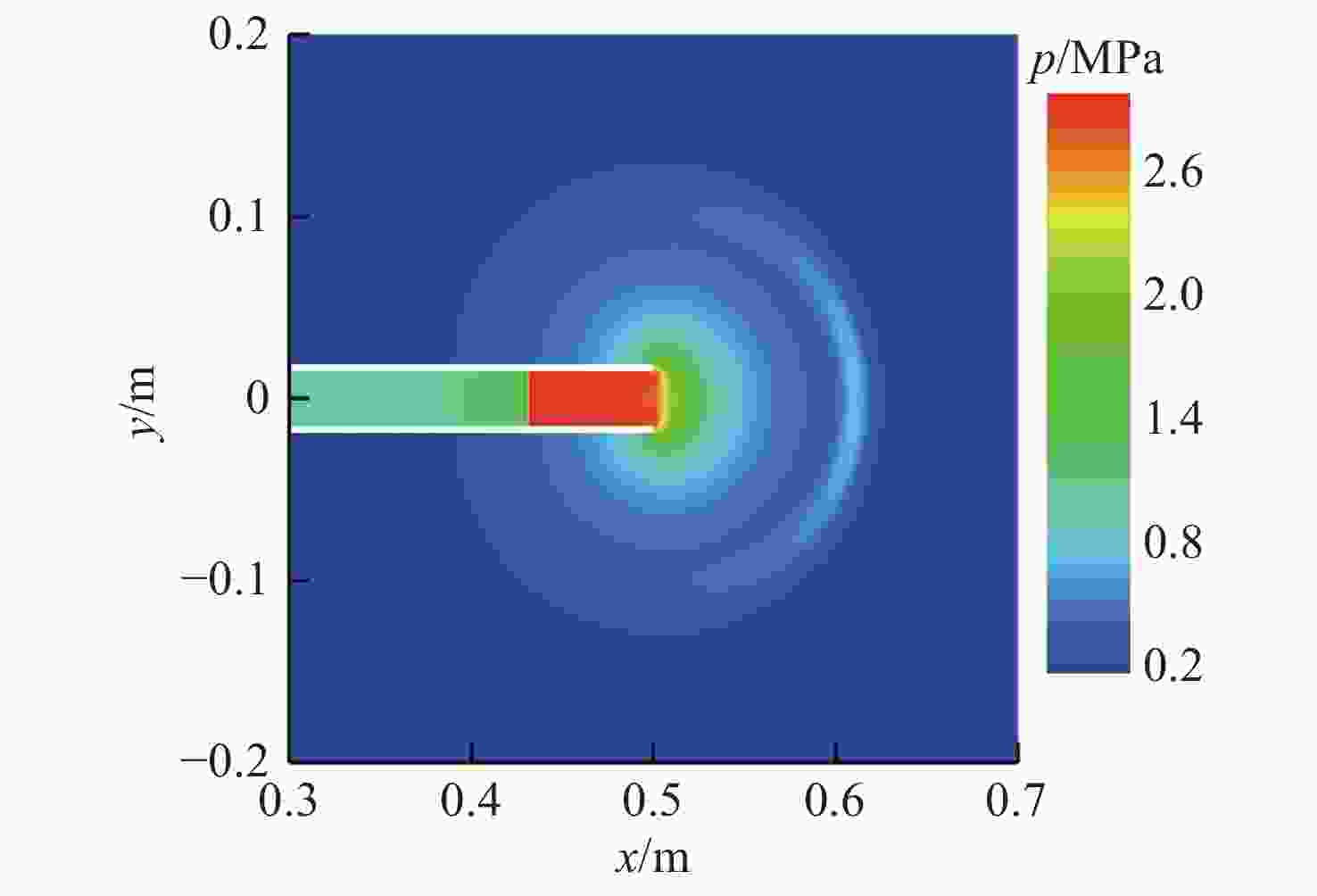
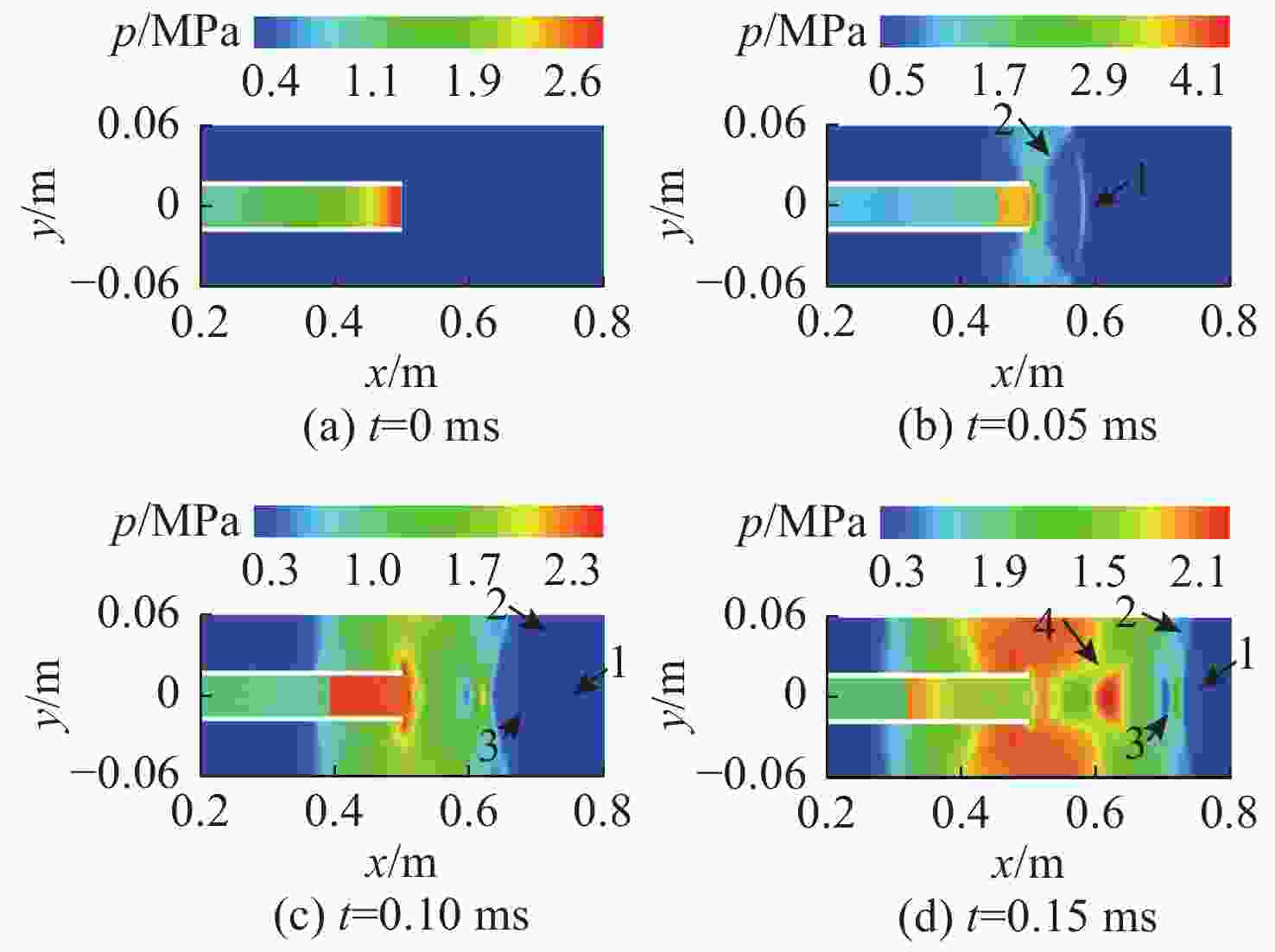
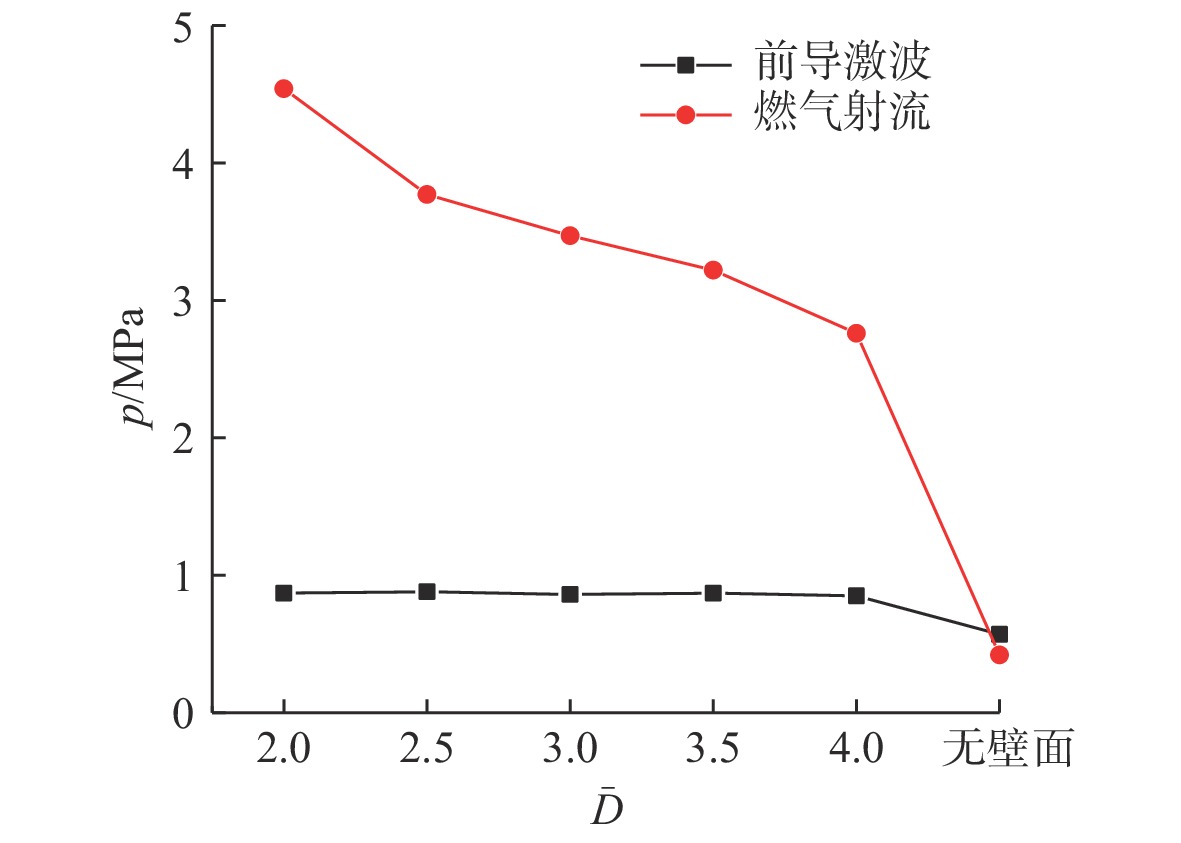
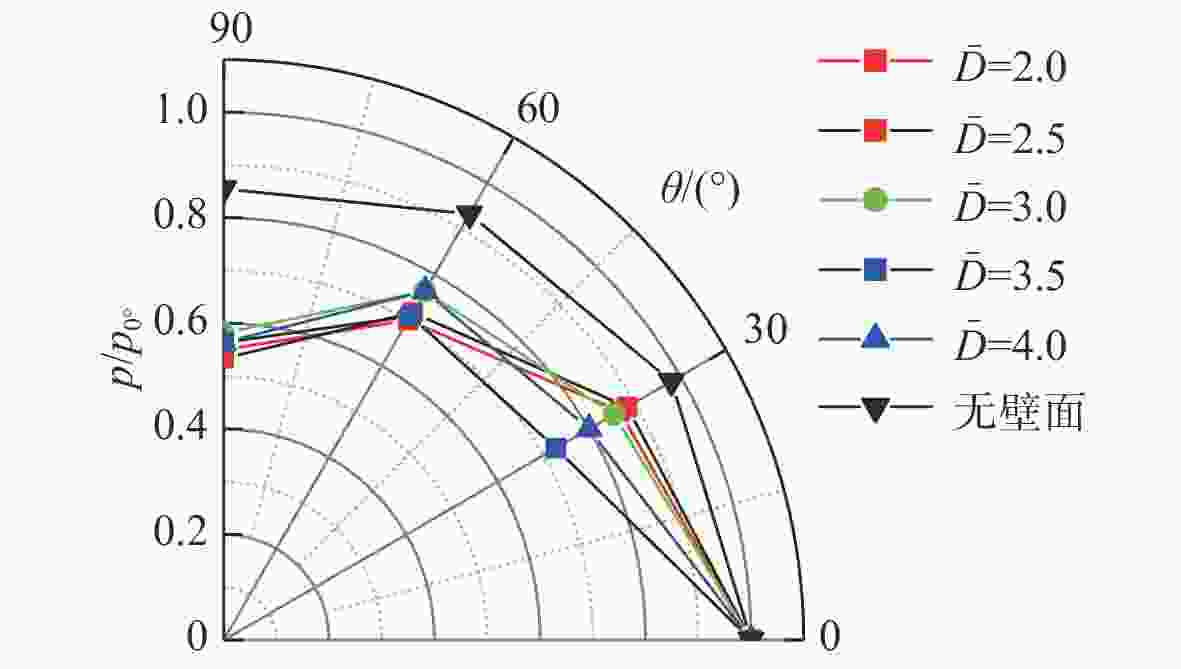
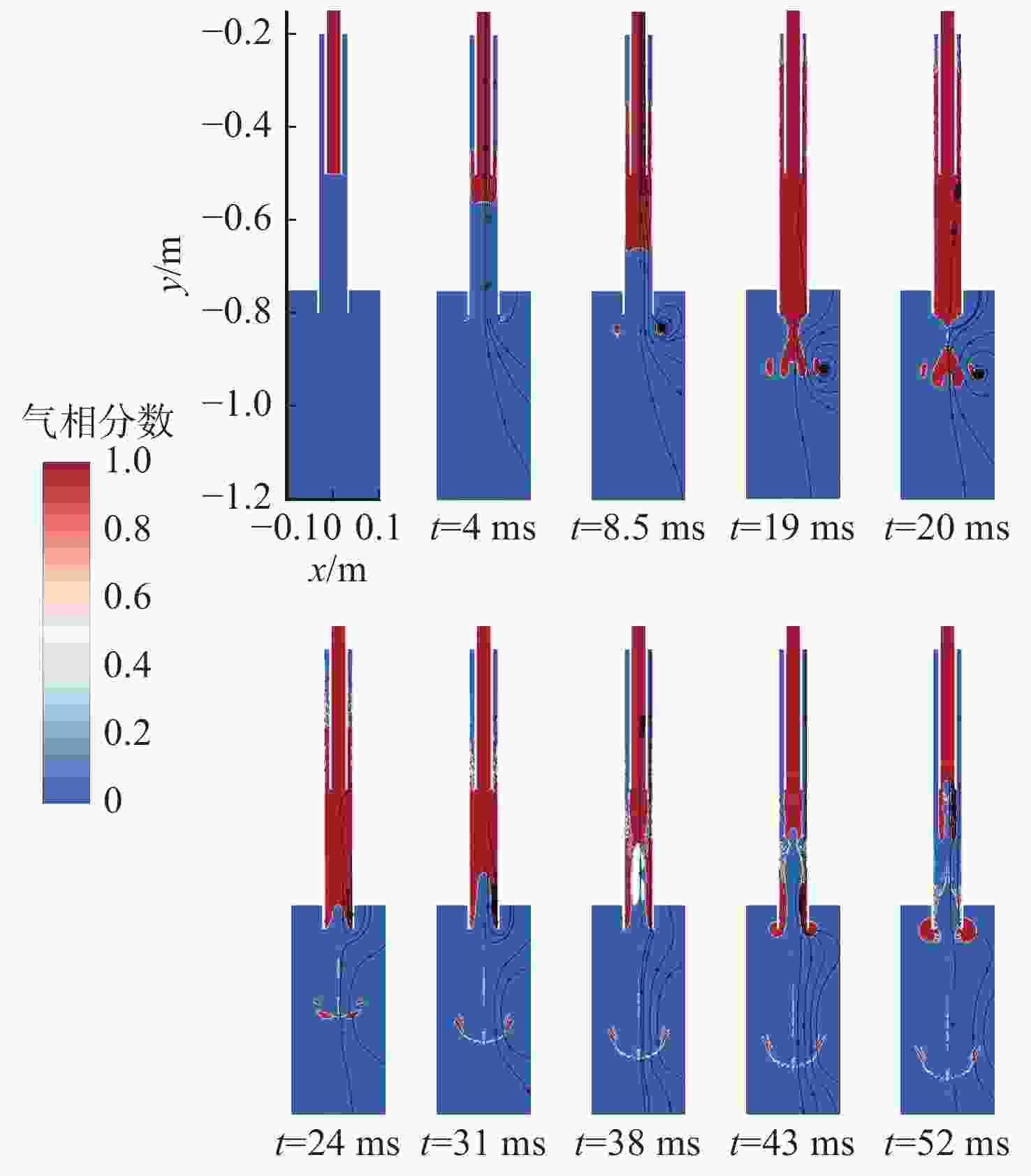
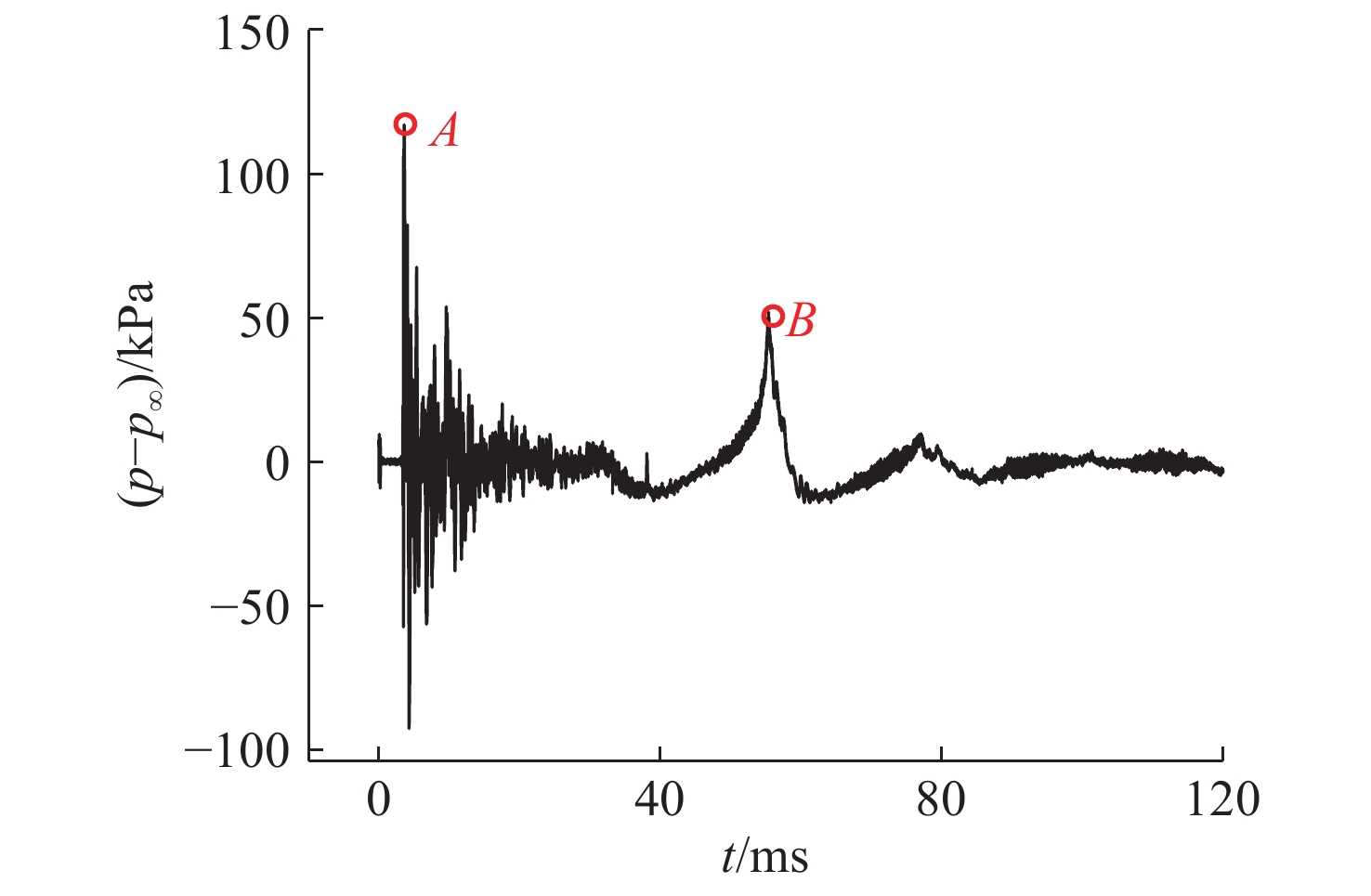
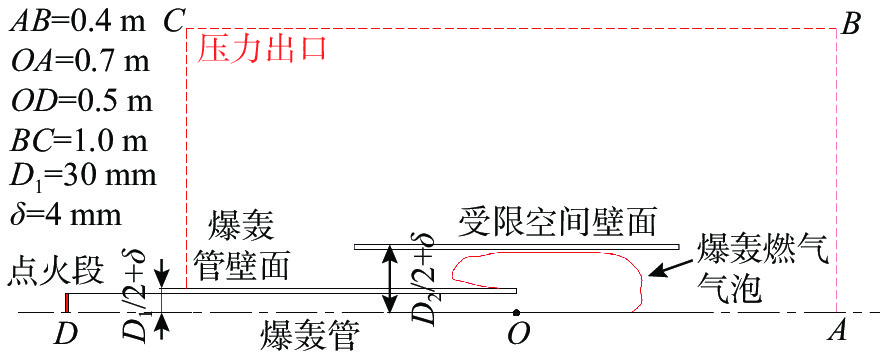
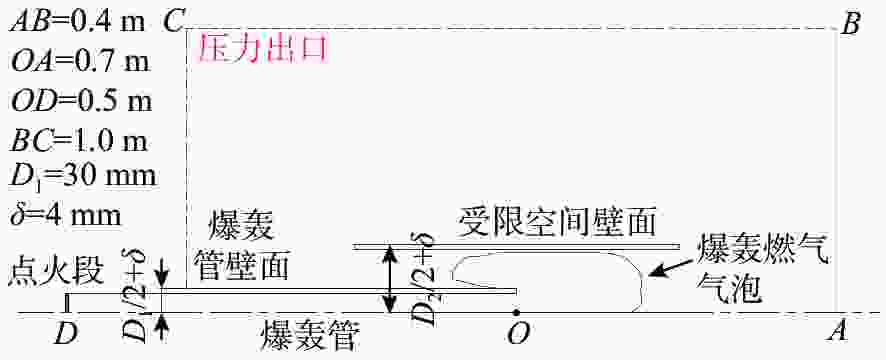
摘要: 为探索脉冲爆轰水冲压发动机水下工作时导水器内燃气射流发展特性, 利用可燃气体的爆轰在水下受限空间内产生脉动气泡, 对爆轰管在圆筒形受限空间内的水下爆轰燃气射流进行了数值仿真与实验验证。基于雷诺时均基本方程组与k-ε两方程模型耦合流体体积气液界面追踪方法的相输运方程建立受限空间中水下单次燃气射流流场流动模型, 使用OpenFOAM中的Compressible Inter Foam求解器对受限空间中脉冲爆轰燃气射流进行数值求解。结果表明: 受限空间对水下爆轰的前导激波的影响较小, 前导激波幅值与自由空间相比变化不大, 由爆轰燃气射流所引起的压力扰动大幅升高且持续时间明显增加, 受限空间中各处压力显著高于受限空间之外; 受限空间中燃气泡的脉动周期延长至60 ms左右, 然而受限空间径向尺寸对燃气泡的脉动周期影响较小。可见, 受限空间可提高水下爆轰管出口近场压力并延长燃气射流作用时间, 研究结果对脉冲爆轰水冲压发动机推力性能提升方法研究具有重要指导作用。
-
关键词:
- 脉冲爆轰水冲压发动机 /
- 水下燃气射流 /
- 受限空间 /
- 气泡脉动
Abstract: To explore the development characteristics of gas jets generated by pulsed detonation water ramjet engines working underwater in water deflectors, numerical simulations and experimental validations were conducted on underwater detonation gas jets generated by detonation tube within a cylindrical confined space by utilizing the detonation of combustible gases to generate pulsating bubbles in the underwater confined space. A flow field model of a single gas jet in an underwater confined space was established based on the Reynolds-averaged equations, the k-ε two-equation model, and the gas-liquid interface tracking method of the volume of fluid(VOF) coupled with the phase transportation equation. The Compressible Inter Foam solver in OpenFOAM was employed for numerically solving pulsed detonation gas jets in the confined space. The results show that the influence of confined space on the leading shock wave of underwater detonation is slight, and the amplitude of the leading shock wave changes insignificantly compared to that in free underwater space. However, the pressure disturbance caused by the detonation gas jet significantly increases, and its duration is prolonged. Additionally, it leads to a noticeable increase in pressure within the confined space compared to that outside the confined space. The pulsation period of bubbles in the confined space is extended to approximately 60 ms, and the radial dimension of the confined space has little effect on the fluctuation period of the bubbles. Therefore, it can be seen that confined space can increase the near-field pressure at the outlet of the underwater detonation tube and extend the action time of the gas jet. The research results are of important guiding significance for the study of thrust performance improvement methods for pulsed detonation water ramjet engines. -
图 1 计算域及边界条件示意图
Figure 1. Schematic diagram of calculated domain and boundary conditions
图 2 点火后不同时刻爆轰管轴线压力分布
Figure 2. Axial pressure distribution of detonation pipe at different times after ignition
图 3 t = 0.05 ms时刻爆轰管轴线处压力分布
Figure 3. The pressure distribution at the axial location of the detonation tube at t = 0.05 ms
图 4 水下自由空间内爆轰管管口附近压力分布云图
Figure 4. Contour of pressure distribution near the detonation tube orifice in underwater free space
图 5 工况3受限空间内压力分布云图
Figure 5. Pressure distribution contours in confined space under working condition 3
图 6 爆轰管出口下游中心轴线100 mm处压力随时间变化图
Figure 6. Pressure variation with time at the center axis 100 mm downstream of the detonation tube outlet
图 7 受限空间对前导激波和燃气射流压力值的影响
Figure 7. Effect of confined space on the pressure values of the leading shock wave and gas jet
图 8 受限空间和水下自由空间管口下游压力扰动指向性
Figure 8. Directional diagram of pressure disturbance downstream of pipe orifices in confined space and underwater free space
图 9 工况9相分布及流线图
Figure 9. Phase distribution and streamline diagram under working condition 9
图 10 受限空间水下爆轰实验装置示意图
Figure 10. Schematic diagram of underwater explosion experimental installations in a confined space
图 11 工况9 中0 ~ 76.6 ms 气泡变化图
Figure 11. Bubble changes from 0 to 76.6 ms under working condition 9
图 13 气泡面积实验与数值计算数据对比曲线
Figure 13. Comparison of experimental and numerical calculation data for bubble area
表 1 数值仿真计算结果与理论值对比
Table 1. Comparison of numerical simulation results with theoretical values
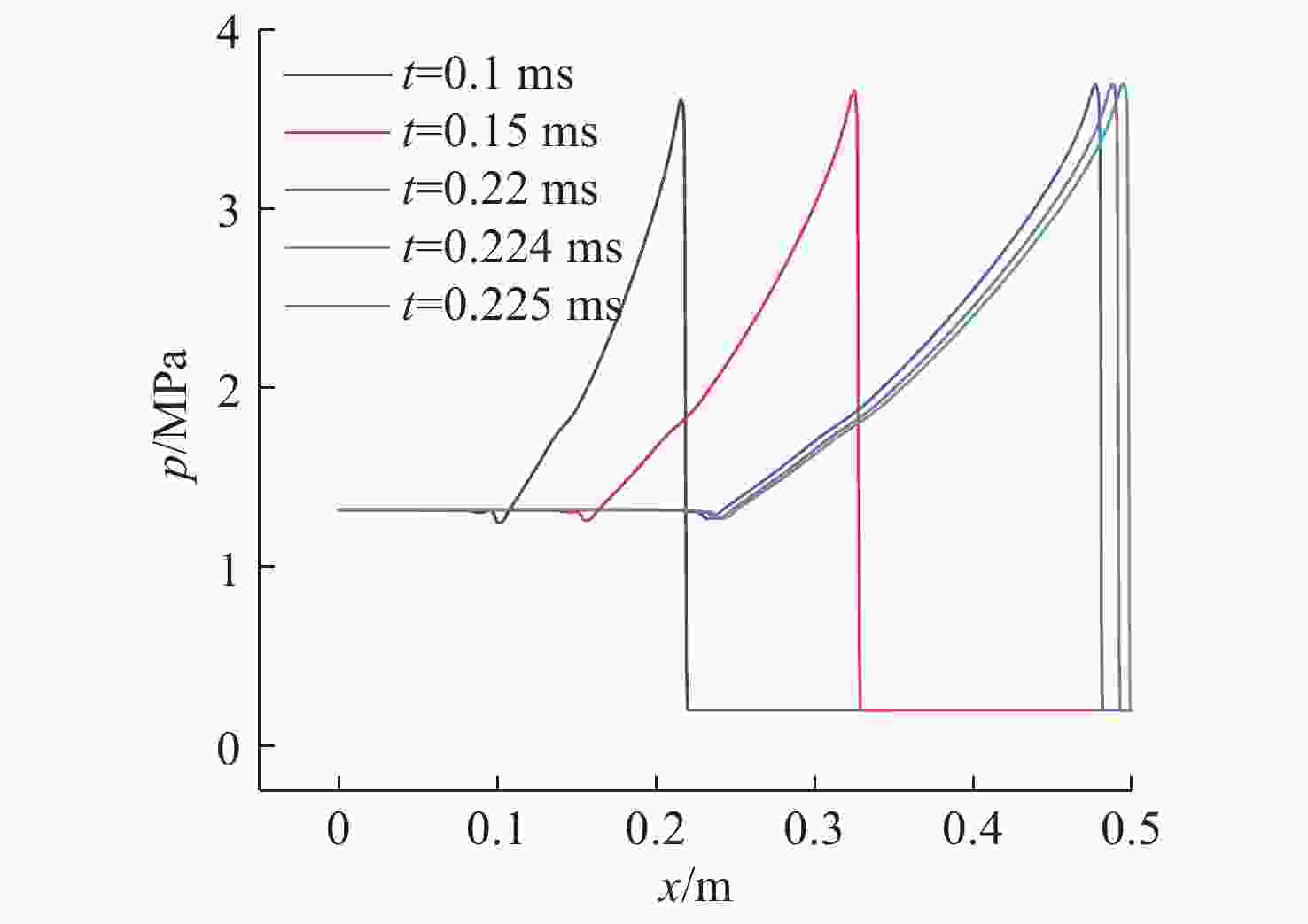
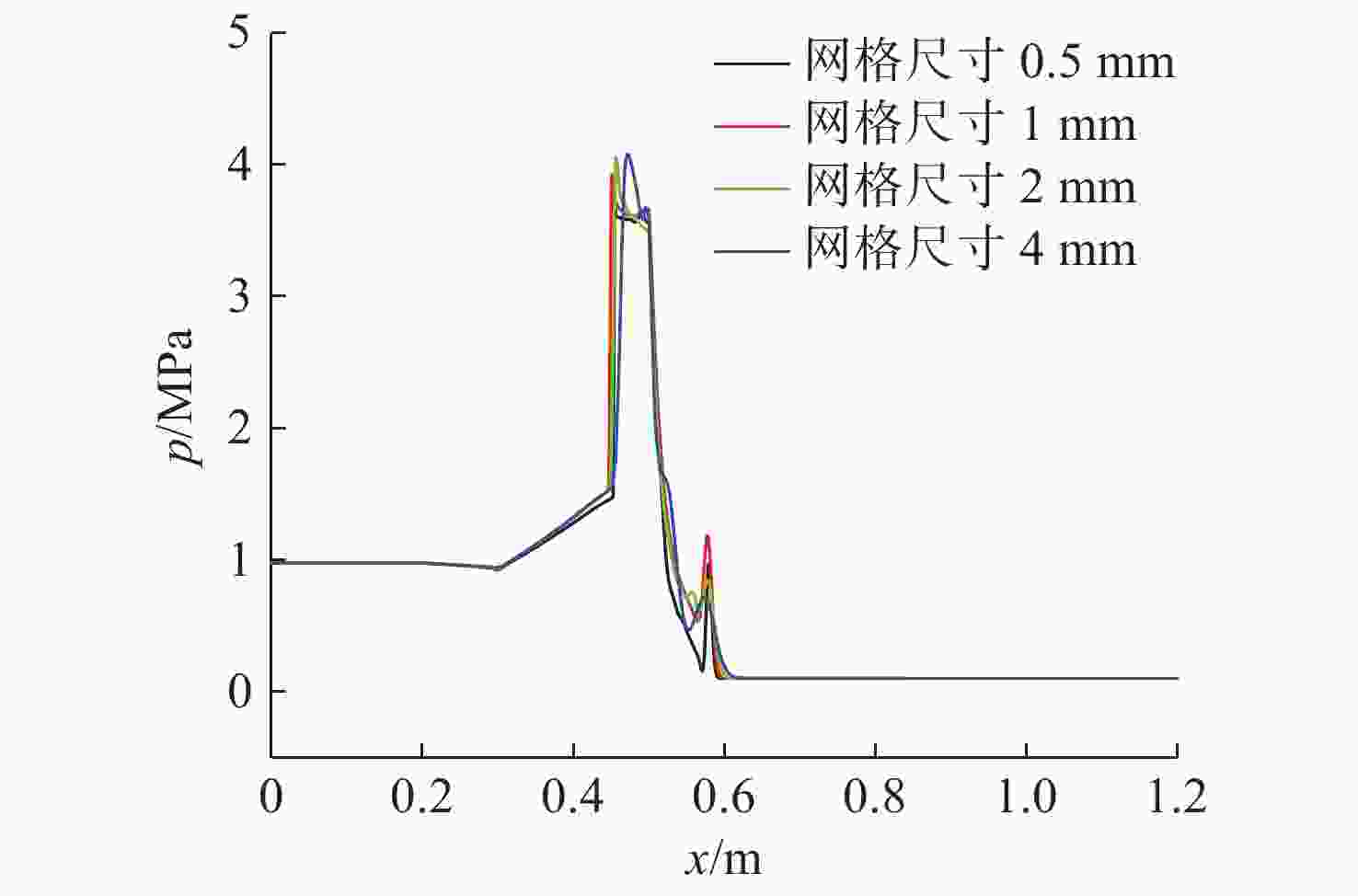
数值 爆轰压力/MPa 爆轰速度/(m/s) C-J理论值 3.364 2 372.9 数值计算结果 3.658 2 182.0 相对误差 8.71% 8.01% 
下载: 导出CSV
表 2 不同网格尺寸下管内反射激波与前导激波压力值
Table 2. Pressure values of reflected shock wave and leading shock wave in tube with different mesh sizes
网格尺寸/mm 管内反射激波
压力峰值/MPa前导激波
压力峰值/MPa0.5 3.88 0.96 1.0 3.92 1.17 2.0 4.05 0.84 4.0 4.08 0.70
下载: 导出CSV
表 3 不同工况参数
Table 3. Parameters under different working conditions
工况序号 爆轰管填充压力/kPa 无量纲
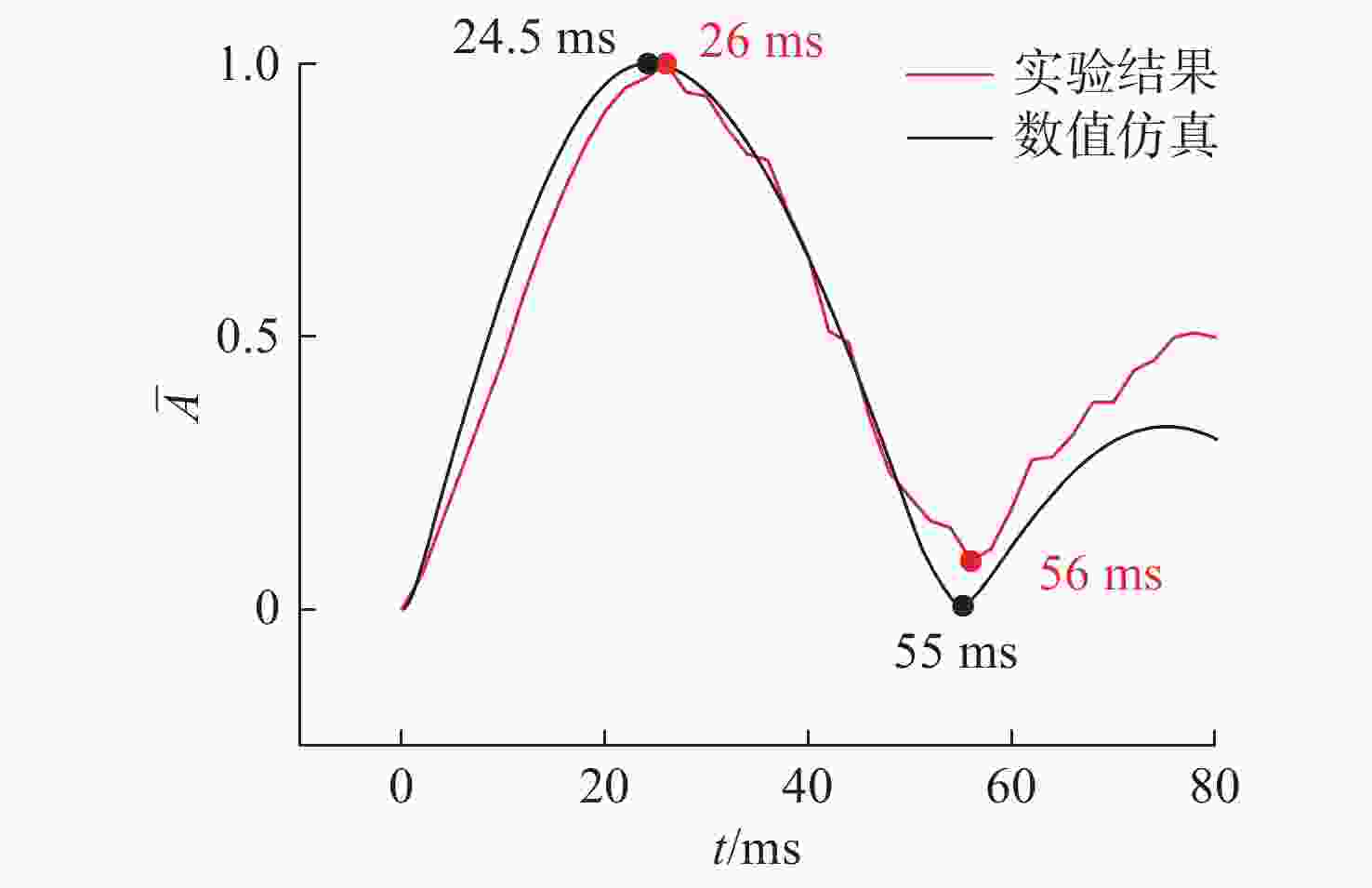
受限空间直径1 1.0 2 2 3 3 4 4 无壁面 5 1.5 2 6 3 7 4 8 无壁面 9 2.0 2 10 3 11 4 12 无壁面
下载: 导出CSV
表 4 燃气泡脉动周期数值计算与实验结果对比
Table 4. Comparison of numerical calculation and experimental results of gas bubble pulsation period
受限空间
直径/mm数值计算
结果/ms实验结果
/ms相对
误差/%120 55.0 57.2 3.8 90 60.5 57.6 4.7 60 60.5 58.0 4.3 无壁面 19.0 20.0 5.0
下载: 导出CSV
-
[1] Lee J H S. The detonation phenomenon[M]. Cambridge, UK: Cambridge University Press, 2008. [2] Frolov S M, Avdeev K A, Aksenov V S, et al. Experimental and computational studies of shock wave-to-bubbly water momentum transfer[J]. International Journal of Multiphase Flow, 2017, 92: 20-38. doi: 10.1016/j.ijmultiphaseflow.2017.01.016 [3] Frolov S M, Avdeev K A, Aksenov V S, et al. Pulsed detonation hydroramjet: Simulations and experiments[J]. Shock Waves, 2020, 30: 221-234. doi: 10.1007/s00193-019-00906-2 [4] 施红辉, 郭强, 王超, 等. 水下超音速气体射流胀鼓与回击的关联性研究[J]. 力学学报, 2010, 42(6): 1206-1210.Shi Honghui, Guo Qiang, Wang Chao, et al. Experiments on the relationship between bulging and back-attack of submerged supersonic gas jets[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1206-1210. [5] 魏英杰, 付英杰, 张嘉钟. 结构参数对两相冲压发动机喷管性能影响分析[J]. 推进技术, 2009, 30(5): 544-550.Wei Yingjie, Fu Yingjie, Zhang Jiazhong. Effect of structure parameter on nozzle performance of bubbly water ramjet engine[J]. Journal of Propulsion Technology, 2009, 30(5): 544-550. [6] 王乐勤, 郝宗睿, 吴大转. 水下气体射流初期流场的数值研究[J]. 工程热物理学报, 2009, 30(7): 1132-1135.Wang Leqin, Hao Zongrui, Wu Dazhuan. et al. Numerical study of the initial flow field of underwater gas jets[J]. Journal of Engineering Themophysics, 2009, 30(7): 1132-1135. [7] Zhang A M, Li S M, Cui P, et al. A unified theory for bubble dynamics[J]. Physics of Fluids, 2023, 35(3): 033323. doi: 10.1063/5.0145415 [8] Tang H, Liu Y L, Cui P, et al. Numerical study on the bubble dynamics in a broken confined domain[J]. 水动力学研究与进展: 英文版, 2020, 32(6): 1029-1042.Tang H, Liu Y L, Cui P, et al. Numerical study on the bubble dynamics in a broken confined domain[J]. Journal of Hydrodynamics, 2020, 32(6): 1029-1042. [9] Li S M, Zhang A M, Cui P, et al. Vertically neutral collapse of a pulsating bubble at the corner of a free surface and a rigid wall[J]. Journal of Fluid Mechanics, 2023, 962(A28): 1-41. [10] Nie B C, Li J C, Zhang H Q. Interaction between reflected shock and bubble in near-wall underwater explosion[J]. Procedia Engineering, 2015, 126: 344-348. doi: 10.1016/j.proeng.2015.11.205 [11] Tian Z L, Liu Y L, Zhang A M, et al. Jet development and impact load of underwater explosion bubble on solid wall[J]. Applied Ocean Research, 2020, 95: 102013. doi: 10.1016/j.apor.2019.102013 [12] 周帏, 翁春生. PDE 出口爆轰波与射流诱发水中流场变化规律的数值仿真[J]. 水下无人系统学报, 2017, 25(3): 167-173.Zhou Wei, Wong Chunsheng. Numerical simulation of the underwater flow field induced by detonation wave and jet from pulse detonation engine outlet[J]. Journal of Unmanned Undersea Systems, 2017, 25(3): 167-173. [13] Liu W, Li N, Weng C, et al. Bubble dynamics and pressure field characteristics of underwater detonation gas jet generated by a detonation tube[J]. Physics of Fluids, 2021, 33(2): 023302. doi: 10.1063/5.0029729 [14] Wang C, Li N, Huang X, et al. Shock wave and bubble pulsation characteristics in a field generated by single underwater detonation[J]. Physics of Fluids, 2022, 34(6): 066108. doi: 10.1063/5.0093978 [15] Wang S P, Wang Q, Zhang A M, et al. Experimental observations of the behaviour of a bubble inside a circular rigid tube[J]. International Journal of Multiphase Flow, 2019, 121: 103096. doi: 10.1016/j.ijmultiphaseflow.2019.103096 [16] Hou Z, Li N, Huang X, et al. Three-dimensional numerical simulation on near-field pressure evolution of dual-tube underwater detonation[J]. Physics of Fluids, 2022, 34(3): 033304. doi: 10.1063/5.0086527 [17] 侯子伟, 翁春生, 贾芳, 等. 水下爆轰燃气泡形态与激波传播过程研究[J]. 推进技术, 2021, 42(4): 755-764.Hou Ziwei, Wong Chunsheng, Jia Fang, et al. Study on the morphology and shock wave propagation process of underwater detonation gas bubble[J]. Journal of Propulsion Technology, 2021, 42(4): 755-764. [18] Hou Z, Li N, Huang X, et al. Experimental study on pressure evolution of detonation waves penetrating into water[J]. Physics of Fluids, 2022, 34(7): 076110. doi: 10.1063/5.0100446 [19] 刘威, 翁春生, 李宁, 等. 脉冲爆轰发动机水下单次爆轰燃气射流初期流场特性[J]. 兵工学报, 2020, 41(z1): 104-109.Liu Wei, Wong Chunsheng, Li Ning, et al. Initial flow field characteristics of gas jet in underwater[J]. Acta Armamentarii, 2020, 41(z1): 104-109. [20] Liu W, Li N, Huang X, et al. Experimental study of underwater pulse detonation gas jets: Bubble velocity field and time-frequency characteristics of pressure field[J]. Physics of Fluids, 2021, 33(8): 083324. doi: 10.1063/5.0060686 [21] Wang C, Li N, Huang X, et al. Investigation of the effect of nozzle on underwater detonation shock wave and bubble pulsation[J]. Energies, 2022, 15(9): 3194. doi: 10.3390/en15093194 [22] Cui P, Zhang A M, Wang S P. Small-charge underwater explosion bubble experiments under various boundary conditions[J]. Physics of Fluids, 2016, 28(11): 117103. doi: 10.1063/1.4967700 [23] 徐泽. 气泡两相冲压发动机工作过程研究[D]. 长沙: 国防科学技术大学, 2015. [24] Zhang J, Xia Z, Huang L, et al. Predicted performance of a two-phase underwater ramjet with a Laval nozzle[J]. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2019, 233(3): 937-948. doi: 10.1177/1475090218795585 [25] Zhang X, Li S, Yu D, et al. The evolution of interfaces for underwater supersonic gas jets[J]. Water, 2020, 12(2): 488. doi: 10.3390/w12020488 -
点击查看大图
计量
- 文章访问数: 261
- HTML全文浏览量: 85
- PDF下载量: 35
- 被引次数: 0
