Numerical Simulation Accuracy Study of Underwater Explosion Shock Waves
-
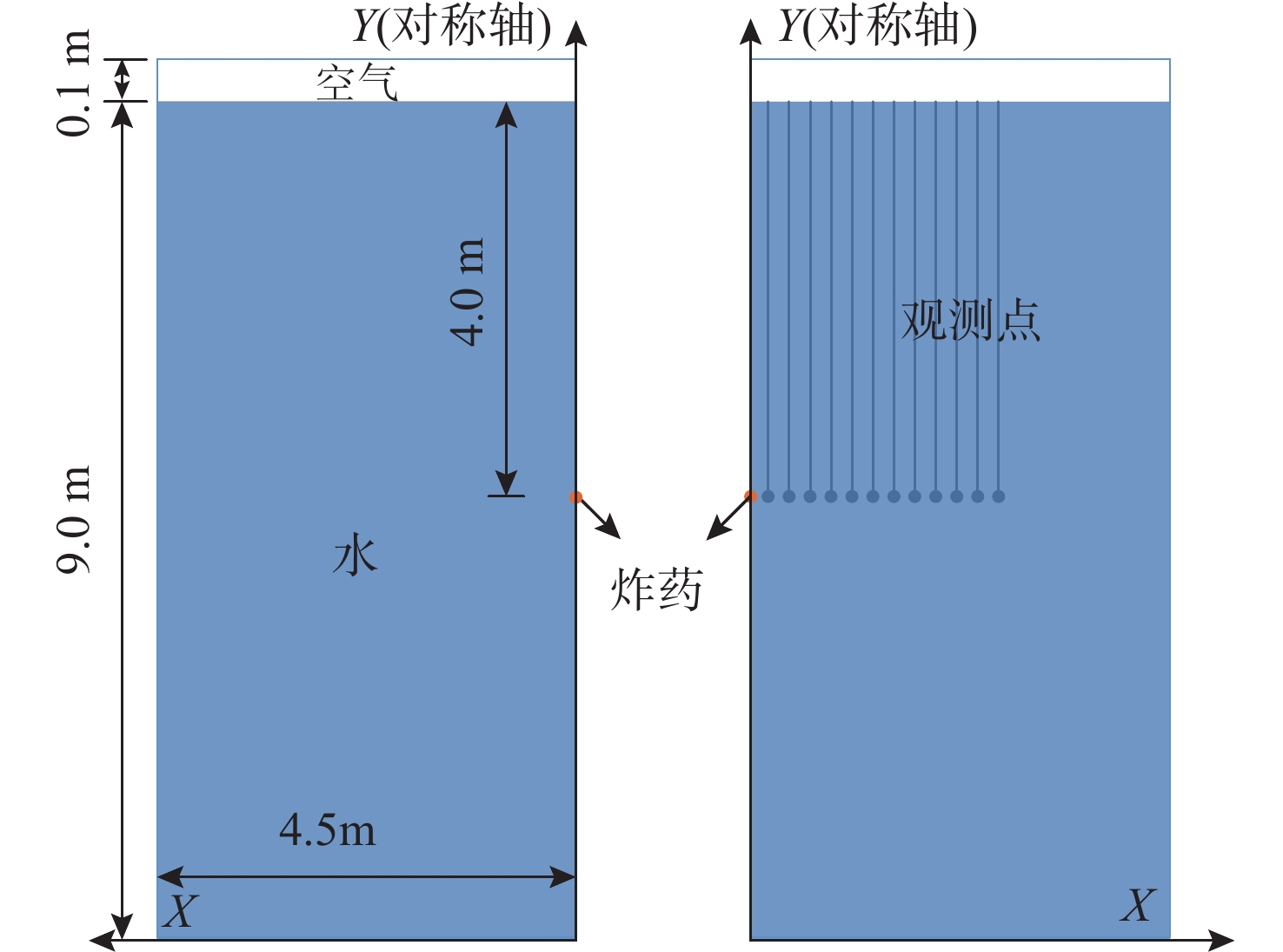
摘要: 在水下爆炸数值仿真研究中, 网格尺寸和一次项人工粘性系数对冲击波峰值压力计算结果有较大影响。在预定计算精度条件下, 快速确定网格尺寸及人工粘性对数值计算意义重大。为此, 文中基于LS-DYNA有限元软件, 建立78 g三硝基甲苯(TNT)二维水下爆炸数值计算模型, 重点分析网格尺寸和一次项粘性系数对水下爆炸冲击波峰值压力和整体计算误差的影响规律。结果表明, 随着网格密度因子的增大, 计算峰值压力对网格的敏感性降低, 且网格密度较大时, 过小的一次项系数会导致计算峰值压力与经验公式值的相对误差增大。在此基础上获得20%范围内误差与网格尺寸、粘性系数之间的关系, 并构建出可用于快速确定网格尺寸和一次项人工粘性系数的误差预估模型, 通过0.2 ~5 000 kg范围内的TNT柱形装药(长径比为1)和球形装药的水下爆炸计算, 验证了预估模型的普适性, 可为二维中近场范围内的水下爆炸冲击波数值仿真计算研究提供参考。Abstract: In the numerical simulation study of the underwater explosion, the grid size and the artificial viscosity coefficient of the primary term have a large impact on the calculation results of the peak pressure of the shock wave. Under the condition of predetermined calculation accuracy, it is of great significance to quickly determine the grid size and artificial viscosity for numerical calculation. For this reason, based on LS-DYNA finite element software, a two-dimensional underwater explosion numerical calculation model of 78 g trinitrotoluene (TNT) was established to analyze the influence of the grid size and the viscosity coefficient of the primary term on the peak pressure of the underwater explosion shock wave and the overall calculation error. The results show that with the increase in the grid density factor, the sensitivity of calculated peak pressure to the grid decreases. When the grid density is larger, a small primary term coefficient will cause the relative error between the calculated peak pressure and the empirical formula value to increase. On this basis, the relationship among the error, grid size, and viscosity coefficient within 20% is obtained, and an error prediction model that can be used to quickly determine the grid size and the artificial viscosity coefficient of the primary term is constructed. Through the underwater explosion calculation of cylindrical TNT charge (aspect ratio of 1) and spherical TNTcharge in the range of 0.2–5 000 kg, the universality of the prediction model is verified, which can provide a reference for the numerical simulation of underwater explosion shock wave in the two-dimensional near-field range.
-
图 2 Q2=0.08时, 不同λ时Pm随比例爆距变化曲线
Figure 2. Variation of Pm with scaled blast distance for different λ at Q2=0.08
图 3 Q2=0.08时, 不同比例爆距处Pm随λ变化曲线
Figure 3. Variation of Pm with λ for different scaled blast distances at Q2=0.08
图 5 λ=3时, 不同Q2时Pm随比例爆距变化曲线
Figure 5. Variation of Pm with scaled blast distance for different Q2 at λ=3
图 6 λ=3时, 不同比例爆距处Pm随Q2变化曲线
Figure 6. Variation of Pm with Q2 for different blast scaled distances at λ =3
图 8 限定区间后峰值压力平均误差曲线
Figure 8. Average errors of peak pressure curves after limited interval
图 10 截距-对数粘性系数线性拟合
Figure 10. Linear fitting of intercept-logarithm viscosity coefficient
表 1 TNT状态方程参数
Table 1. State equation parameters for TNT
${A / { {\text{GPa} }} }$ ${B / { {\text{GPa} }} }$ $ {R_1} $ $ {R_2} $ $ \omega $ $ {E / {{\text{GPa}}}} $ 371.20 3.23 4.15 0.95 0.30 7.00 
下载: 导出CSV
表 2 水状态方程参数
Table 2. State equation parameters for water
C/(m/s) $ {S_1} $ $ {S_2} $ $ {S_3} $ $ \alpha $ $E$ $ {V_0} $ 1483 2.106 −0.174 0.01 − − 1.0
下载: 导出CSV
表 3 空气状态方程参数
Table 3. State equation parameters for air
E/(J/kg) C0 C1 C2 C3 C6 $ {C_4} $ $ {C_5} $ 2.5×106 0 0 0 0 0 0.4 0.4
下载: 导出CSV
表 4 不同爆距处峰值压力对比
Table 4. Comparison of peak pressure at different scaled blast distances
MPa Pm Z /(m/kg1/3) 0.75 1.17 1.88 2.80 试验值 70.10 39.60 23.30 15.30 数值解 75.50 42.00 22.70 13.60 经验值 72.60 43.80 25.70 16.40
下载: 导出CSV
表 5 λ=6时, 不同比例爆距处冲击Pm对比
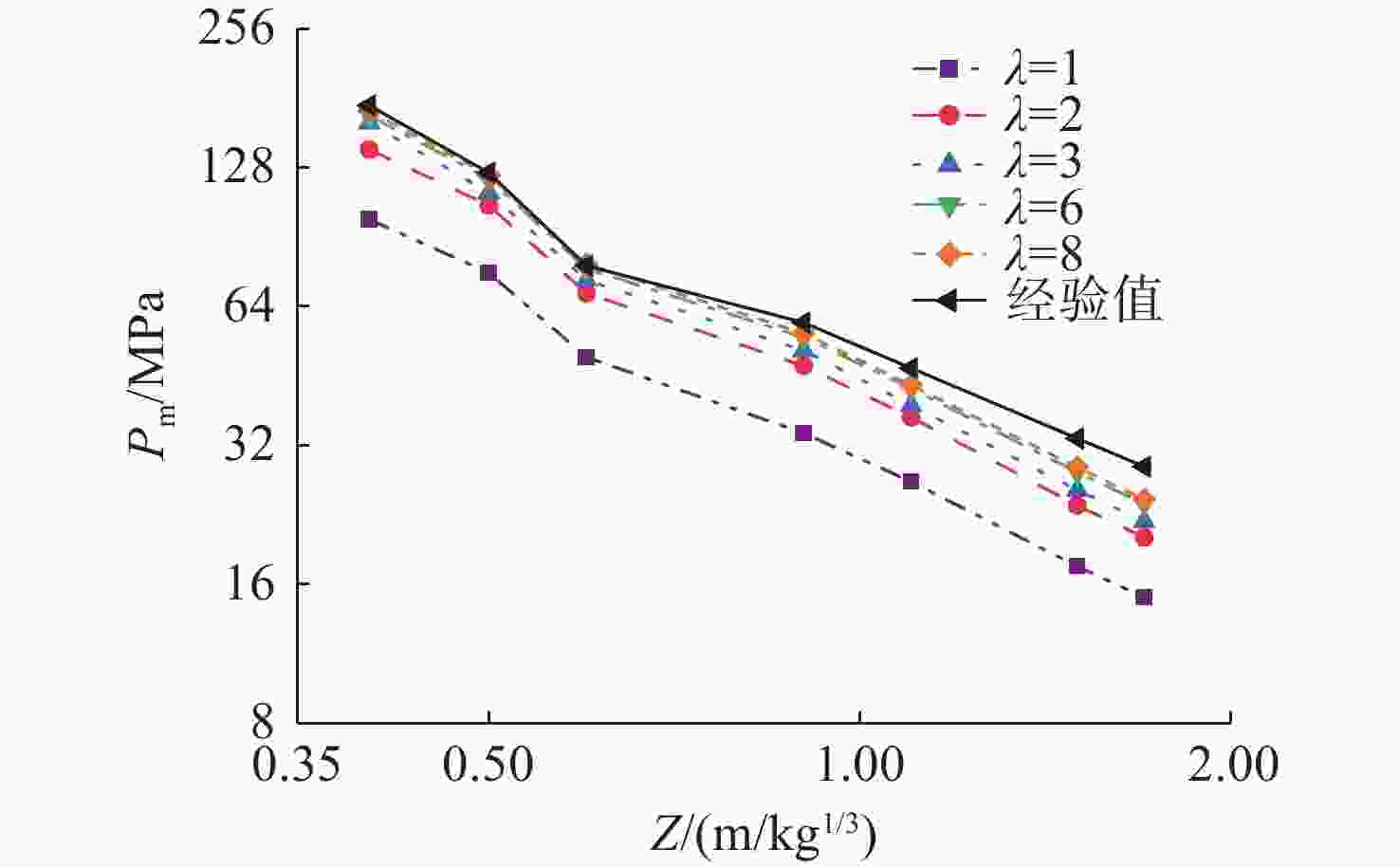
Table 5. Different scaled blast distances peak pressure of shock waves at λ =6
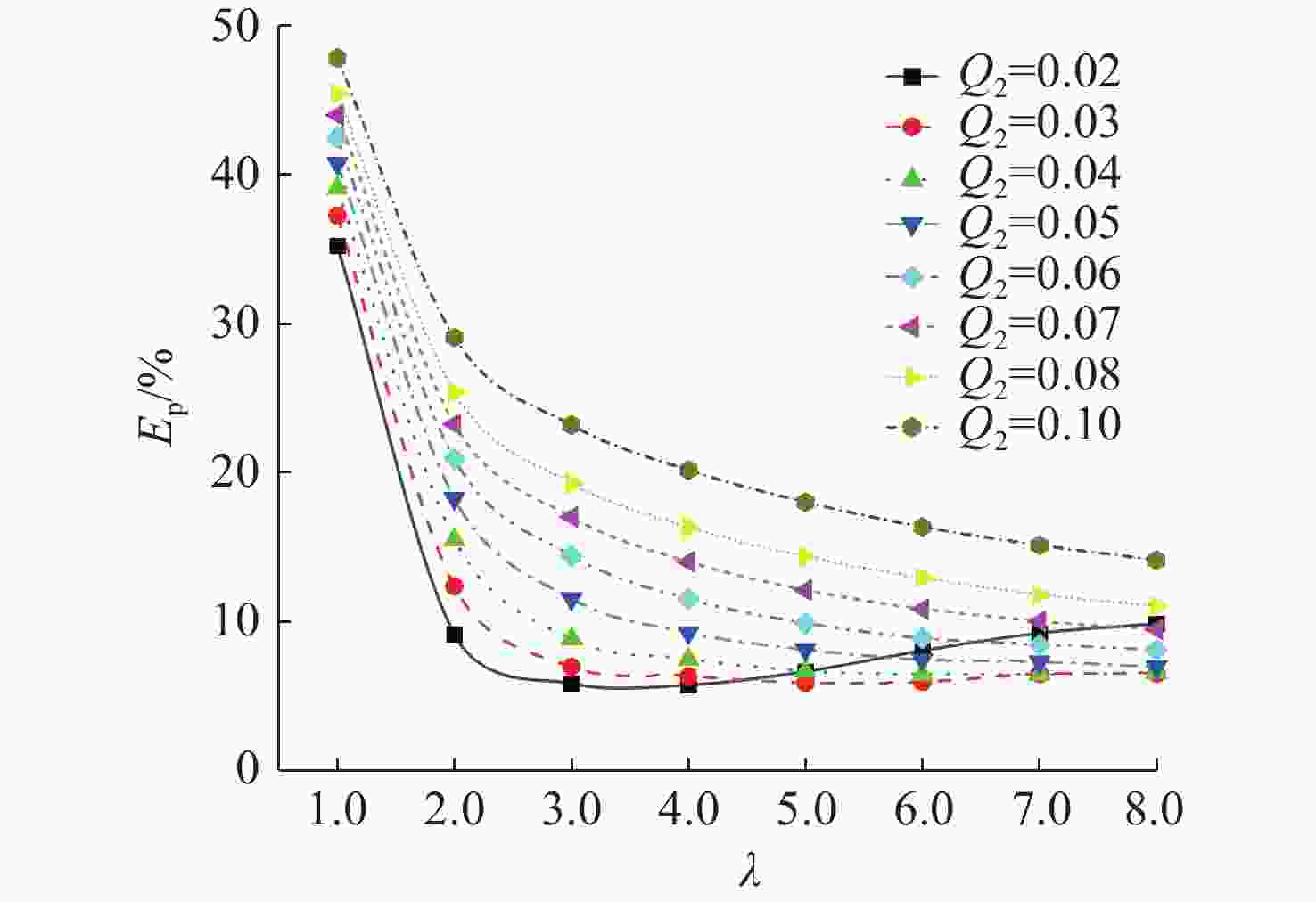
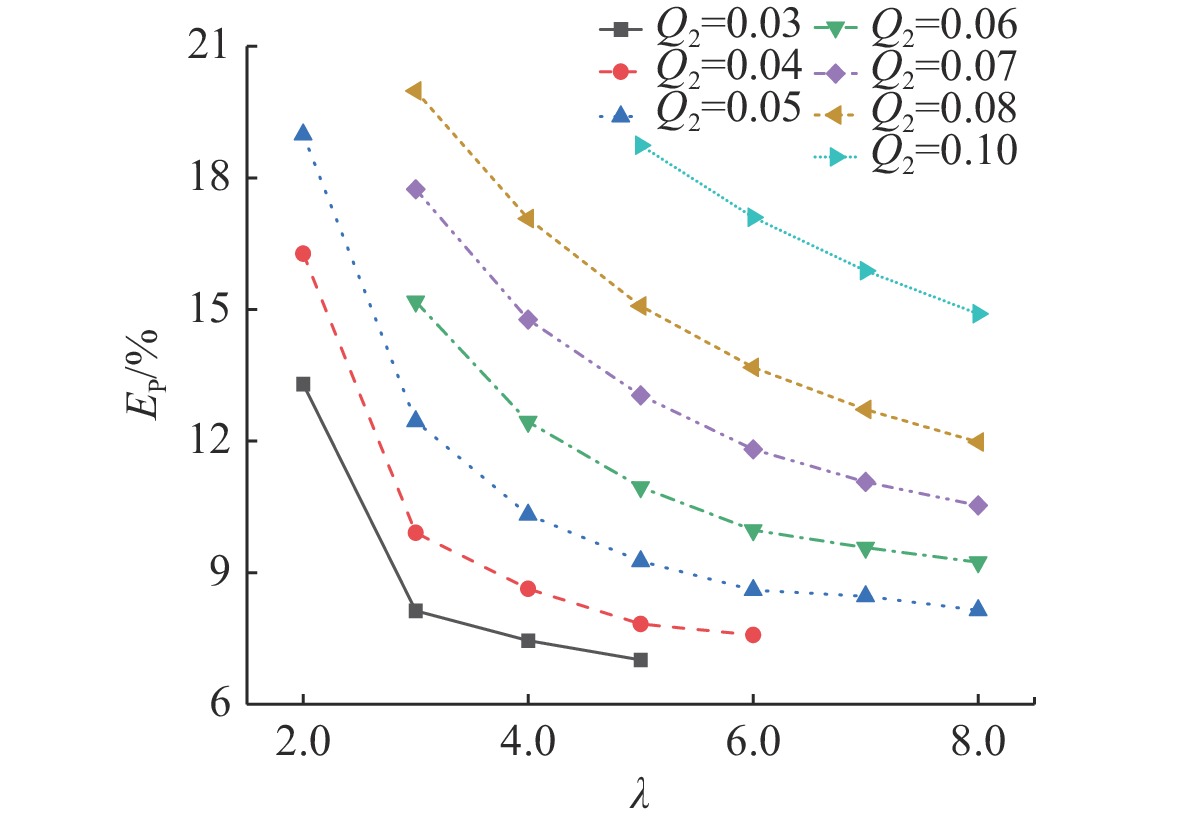
MPa 工况类型 Z/(m/kg−1/3) 0.327 0.500 0.700 0.900 1.170 1.700 Q2=0.020 253.000 138.000 92.800 67.500 48.800 30.700 Q2=0.060 235.000 127.000 81.800 58.300 41.500 25.400 经验值 235.800 124.700 78.400 59.000 43.900 28.800
下载: 导出CSV
表 6 lgEP关于lgλ的拟合参数
Table 6. Fitting parameters for λ in EP
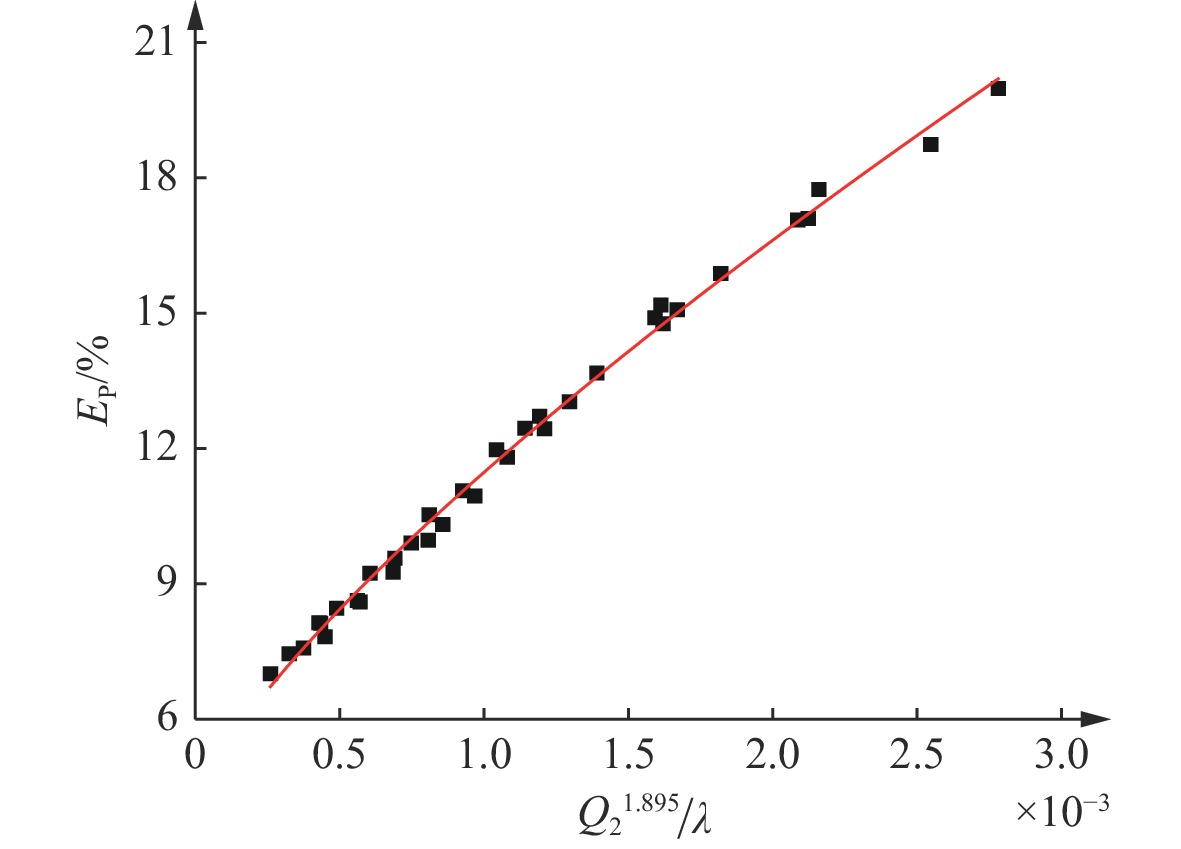
拟合参数 Q2 0.030 0 0.040 0 0.050 0 0.060 0 0.070 0 0.080 0 0.1 000 k −0.690 0 −0.790 0 −0.590 0 −0.510 0 −0.530 0 −0.530 0 −0.490 0 b 1.300 0 1.420 0 1.410 0 1.410 0 1.500 0 1.550 0 1.610 0 R1 0.940 4 0.967 6 0.963 3 0.985 8 0.996 1 0.999 3 0.999 9 R2 0.884 3 0.936 3 0.927 9 0.971 7 0.992 2 0.998 6 0.999 8
下载: 导出CSV
表 7 b关于Q2的拟合参数
Table 7. Fitting parameters for b in Q2
k1 b1 R R2 0.586 0 2.180 0 0.971 6 0.944 1
下载: 导出CSV
表 8 不同工况下峰值压力误差
Table 8. Errors of peak pressure for different operating conditions
装药质量/kg 装药形状 平均误差/% 预估误差/% 0.2 柱形 9.75 10.36 0.2 球形 10.79 5.0 柱形 9.45 5.0 球形 10.45 50.0 柱形 10.83 50.0 球形 10.30 500.0 柱形 9.62 500.0 球形 10.18 1 500.0 柱形 9.57 1 500.0 球形 9.89 5 000.0 柱形 9.58 5 000.0 球形 9.76
下载: 导出CSV
-
[1] 蔡尚. 水下爆炸作用下舰船毁伤效能评估及水雷布阵策略优化研究[D]. 哈尔滨: 哈尔滨工程大学, 2018. [2] 田影. 不同边界条件下近场水下爆炸载荷特性研究[D]. 大连: 大连理工大学, 2022. [3] 辛春亮, 秦健, 刘科种, 等. 基于LS-DYNA软件的水下爆炸数值模拟研究[J]. 弹箭与制导学报, 2008, 28(3): 156-158.Xin Chunliang, Qin Jian, Liu Kezhong, et al. Research on UNDEX numerical simulation based on LS-DYNA[J]. Journal of Projectiles Rockets Missiles and Guidance, 2008, 28(3): 156-158. [4] Huang H, Jiao J Q, Nie X J, et al. Numerical modeling of underwater explosion by one-dimensional ANSYS-AUTODYN[J]. Journal of Energetic Materials, 2011, 29(4): 292-325. doi: 10.1080/07370652.2010.527898 [5] Wang G, Wang Y, Lu W, et al. On the determination of the mesh size for numerical simulations of shock wave propagation in near field underwater explosion[J]. Applied Ocean Research, 2016, 59: 1-9. doi: 10.1016/j.apor.2016.05.011 [6] 胡亮亮, 黄瑞源, 李世超, 等. 水下爆炸冲击波数值仿真研究[J]. 高压物理学报, 2020, 34(1): 102-114.Hu Liangliang, Huang Ruiyuan, Li Shichao, et al. Shock wave simulation of underwater explosion[J]. Chinese Journal of High Pressure Physics, 2020, 34(1): 102-114. [7] 张社荣, 李宏璧, 王高辉, 等. 水下爆炸冲击波数值模拟的网格尺寸确定方法[J]. 振动与冲击, 2015, 34(8): 93-100.Zhang Sherong, Li Hongbi, Wang Gaohui, et al. A method to determine mesh size in numerical simulation of shock wave of underwater explosion[J]. Journal of Vibration and Shock, 2015, 34(8): 93-100. [8] 杨坤, 陈朗, 伍俊英, 等. 计算网格与人工粘性系数对炸药水中爆炸数值模拟计算的影响分析[J]. 兵工学报, 2014, 35(S2): 237-243.Yang Kun, Chen Lang, Wu Junying, et al. The effects of computing grid and artificial viscosity coefficient on underwater explosion numerical simulation[J]. Acta Armamentarii, 2014, 35(S2): 237-243. [9] 闫秋实, 常松. 水下爆炸三维数值模拟特征参量敏感性分析[J]. 北京工业大学学报, 2023, 49(10): 1099-1108.Yan Qiushi, Chang Song. Underwater explosion 3D numerical simulation characteristic parameter sensitivity analysis[J]. Journal of Beijing University of Technology, 2023, 49(10): 1099-1108. [10] 马腾, 王金相, 刘亮涛, 等. 不同长径比柱形装药水下爆炸冲击波演化规律[J]. 振动与冲击, 2022, 41(8): 149-157, 222.Ma Teng, Wang Jinxiang, Liu Liangtao, et al. Shock wave evolution of cylindrical charge with different slender ratios[J]. Journal of Vibration and Shock, 2022, 41(8): 149-157, 222. [11] 孟龙, 黄瑞源, 王金相, 等. 小当量梯恩梯水下爆炸气泡脉动的数值模拟[J]. 兵工学报, 2020, 41(S1): 64-71.Meng Long, Huang Ruiyuan, Wang Jinxiang, et al. Numerical simulation of bubble pulsation of small scaled TNT in underwater explosion[J]. Acta Armamentarii, 2020, 41(S1): 64-71. [12] Huang C, Liu M, Wang B, et al. Underwater explosion of slender explosives: Directional effects of shockwaves and structure responses[J]. International Journal of Impact Engineering, 2019, 130(8): 266-280. [13] Wang J, Yang L, Xu Z, et al. Numerical simulation on underwater explosion in small-sized containers[J]. Mathematical Modelling of Engineering Problems, 2016, 3(3): 151-156. doi: 10.18280/mmep.030307 [14] 高源. 炸药深水爆炸载荷研究[D]. 北京: 北京理工大学, 2021. [15] 辛春亮. 有限元分析常用材料参数手册[M]. 北京: 机械工业出版社, 2022. [16] Cole R H. Underwater explosions[M]. New York: Dover Publications, 1965. [17] Zamyshlyaev B V, Yakovlev Y S. Dynamic loads in underwater explosion[R]. Washington, D. C: Naval Intelligence Support Center, 1973. -
点击查看大图
计量
- 文章访问数: 311
- HTML全文浏览量: 134
- PDF下载量: 29
- 被引次数: 0
