Hydrodynamic Performance of Efficiency Transition Point of Forked Caudal Fins
-
摘要: 鲔科鱼类具有较高的游动速度和游动效率, 因此成为了仿生机器鱼的理想生物原型。为了研究鲔科鱼类叉状尾鳍效率转捩点的水动力特征, 针对推力和功耗的源项进行重点分析。尾鳍模型采用了相同的表面面积、展弦比和叉长。为了统一尾鳍形状的尺度, 采用扫掠角用于表征不同的叉状尾鳍平面结构。研究发现鲔科鱼类尾鳍扫掠角的增加弱化了尾鳍的有效面积, 导致了尾鳍摆动时推动流体向下游运动而受到的反作用力降低, 因此尾鳍的推进能力也会随之衰退。另外, 扫掠角的增加也引起了前缘涡强度的增加和前缘涡的发展, 从而造成了更大的涡增推力。然而, 过分增加扫掠角尽管存在功耗下降的优势, 但也引起推力和水动力效率的下降, 特别是对于高斯特劳哈尔数的情况。通过对推力的源项进行分析发现扫掠角对附加质量力和涡增推力存在相反的作用机制。Abstract: Thunniform fish has high swimming speed and swimming efficiency and thus becomes the ideal biological prototype of bionic robotic fish. In order to study the hydrodynamic characteristics of the efficiency transition point of the forked caudal fins of thunniform fish, the source terms influencing thrust and power consumption were mainly analyzed. The caudal fin model used the same surface area, aspect ratio, and fork length. To unify the metrics about the fin shape, the sweep angle was used to represent the structure for the forked caudal fins in this paper. It is found that the increase in the sweep angle attenuates the available area of the caudal fin of the thunniform fish, resulting in a lower reaction force to push the fluid downstream when the caudal fin swings. As a result, the thrust of the caudal fin decreases. Additionally, the rise in the sweep angle also triggers the enhancement of the strength and the development of the leading-edge vortex, thereby inducing greater vortex-augmented thrusts. However, an excessive increase in the sweep angle may trigger a decline in the thrust and efficiency, especially for a high Strouhal number, along with a decrease in power consumption. It is found that the sweep angle has an opposite action on the added mass force and vortex-augmented thrust by analyzing the source term of thrust.
-
Key words:
- biomimetic robotic fish /
- forked caudal fin /
- hydrodynamic performance /
- vortex
-
图 1 尾鳍模型和扫掠角定义
Figure 1. The shape of the three caudal fin models and the definition of the sweep angle
图 2 平均推力系数和效率随单元数变化曲线(St=0.25)
Figure 2. Curves of average thrust coefficient and efficiency with the number of units(St=0.25)
图 4 3种模型的推进效率(St=0.2~0.3)
Figure 4. Propulsion efficiency of three models with St numbers in the range of 0.2-0.3
图 5 3种模型的时均推力(St=0.2~0.3)
Figure 5. Time-averaged thrust of the three models with St numbers in the range of 0.2-0.3
图 6 3种模型的时均功率(St=0.2~0.3)
Figure 6. Time-averaged power of the three models with St numbers in the range of 0.2-0.3
图 7 推力相对于S×Sr2的关系(St=0.2~0.3)
Figure 7. Thrust as a function of S×Sr2 with St numbers in the range of 0.2-0.3
图 8 功率相对于S×Sr3的关系(St=0.2~0.3)
Figure 8. Power as a function of S×Sr3 with St numbers in the range of 0.2-0.3
图 9 3种模型在3 s时的能量消耗等值面图(St=0.3)
Figure 9. Energy consumption contours of three models at 3 s(St=0.3)
图 10 3种模型尾迹流向方向速度的瞬态等值面图(St=0.25)
Figure 10. Transient contours of wake flow direction velocity for three models at St=0.25
图 11 3种模型在3.16 s、3.28 s和3.48 s的表面压力分布(St=0.25)
Figure 11. Pressure contours of the three models at 3.16 s, 3.28 s and 3.48 s at St=0.25
图 12 3种模型在3.16 s、3.28 s和3.48 s的表面压力分布(St=0.2)
Figure 12. Pressure contours of the three models at 3.16 s, 3.28 s and 3.48 s at St=0.2
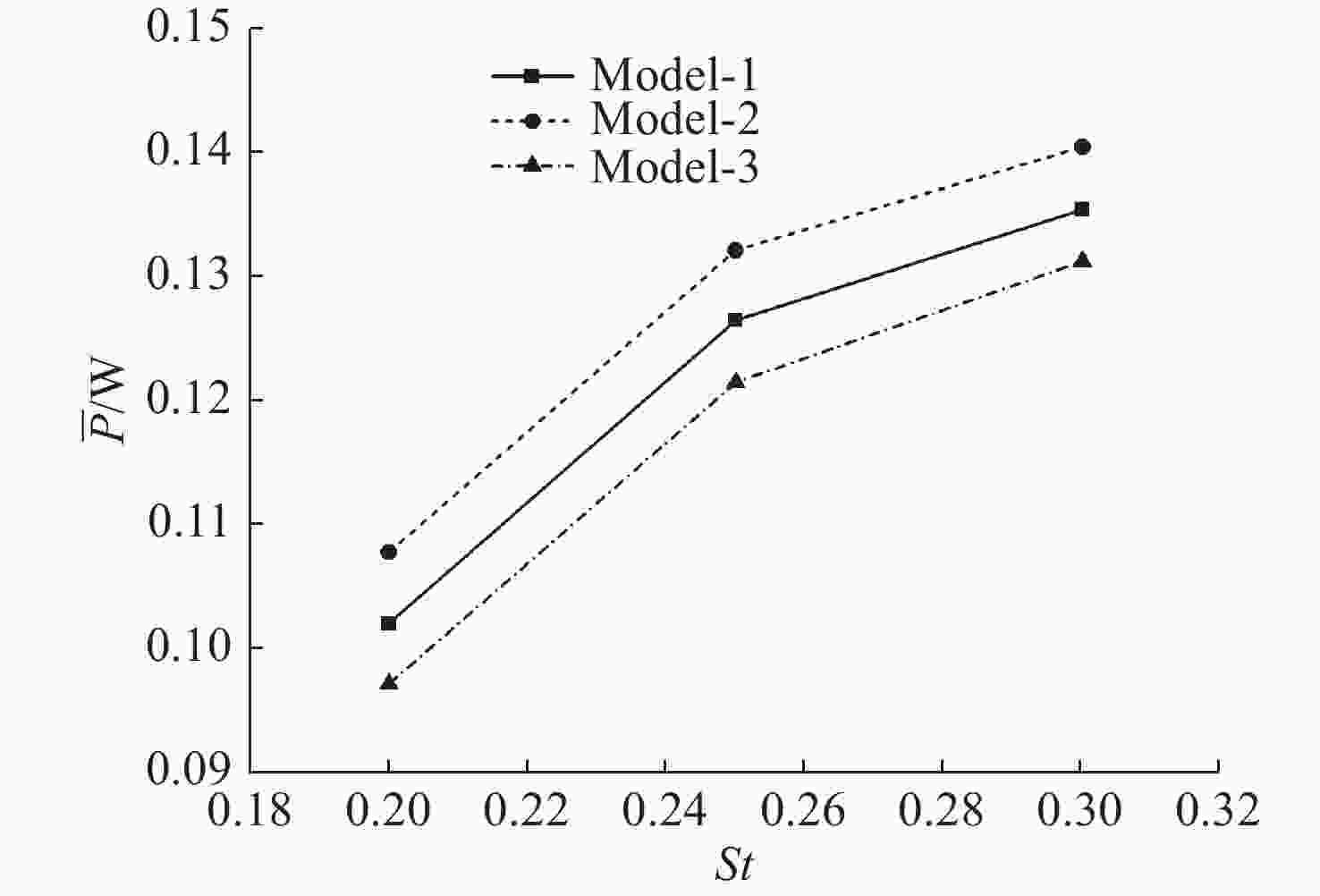
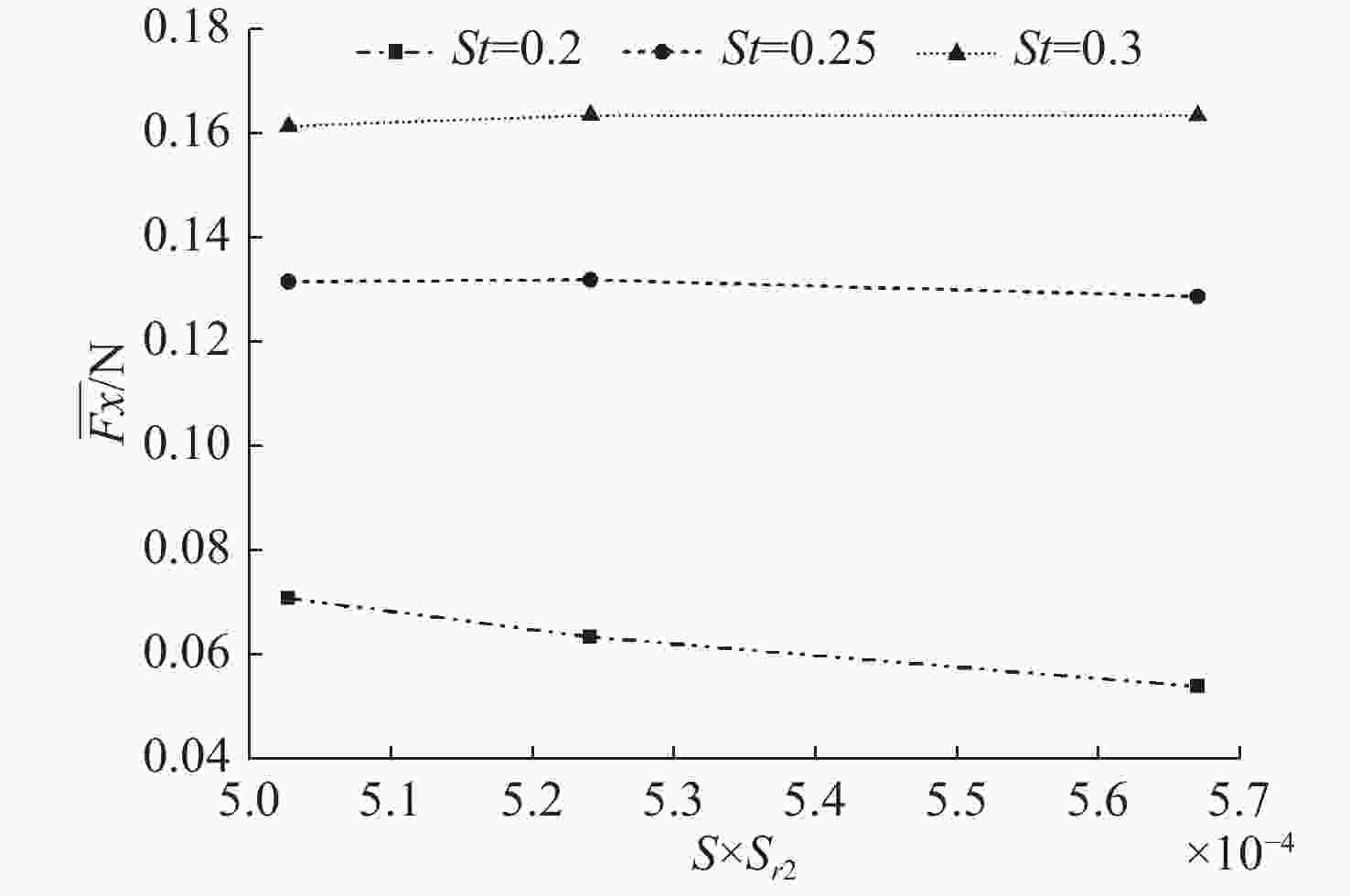
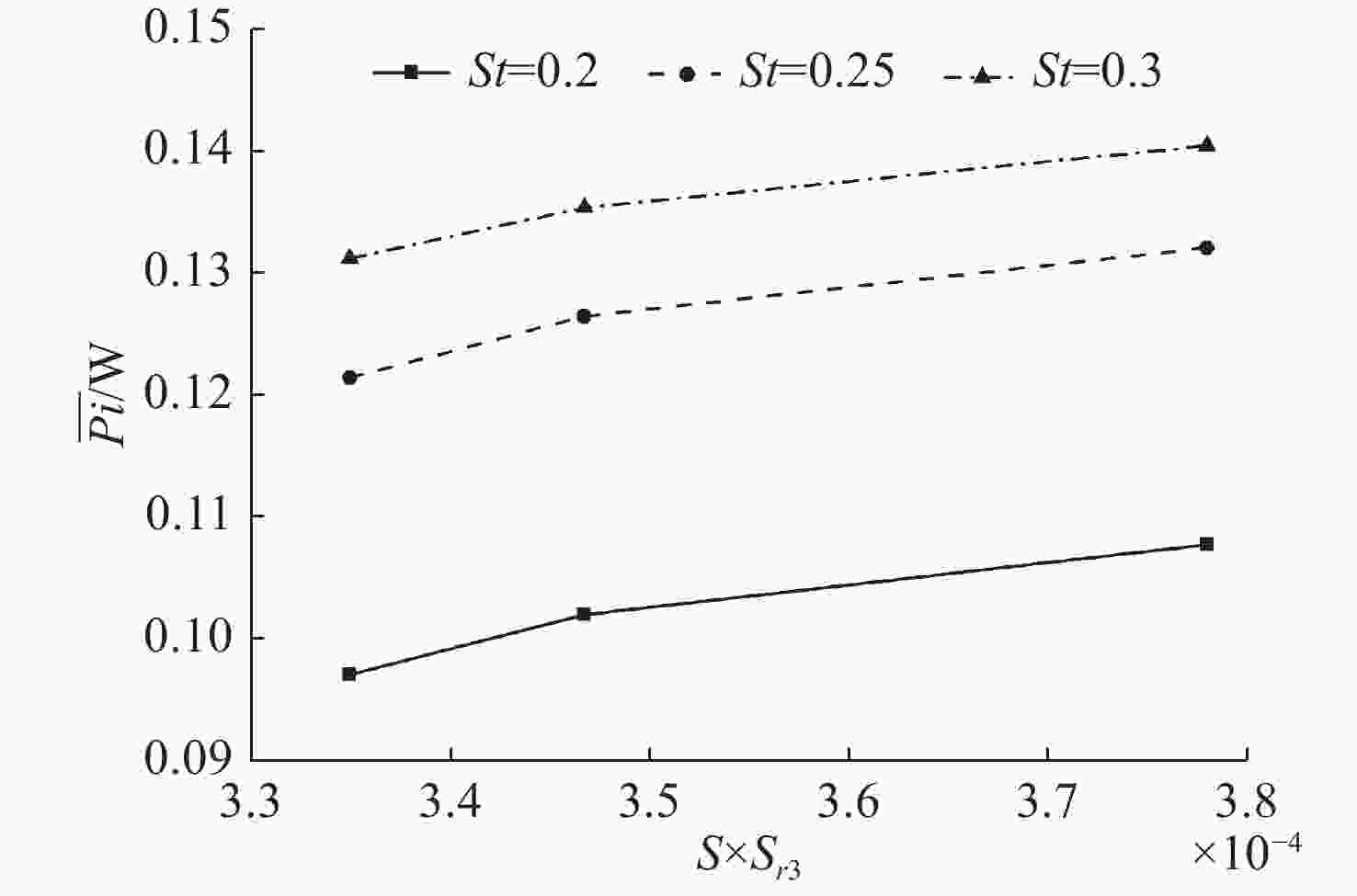
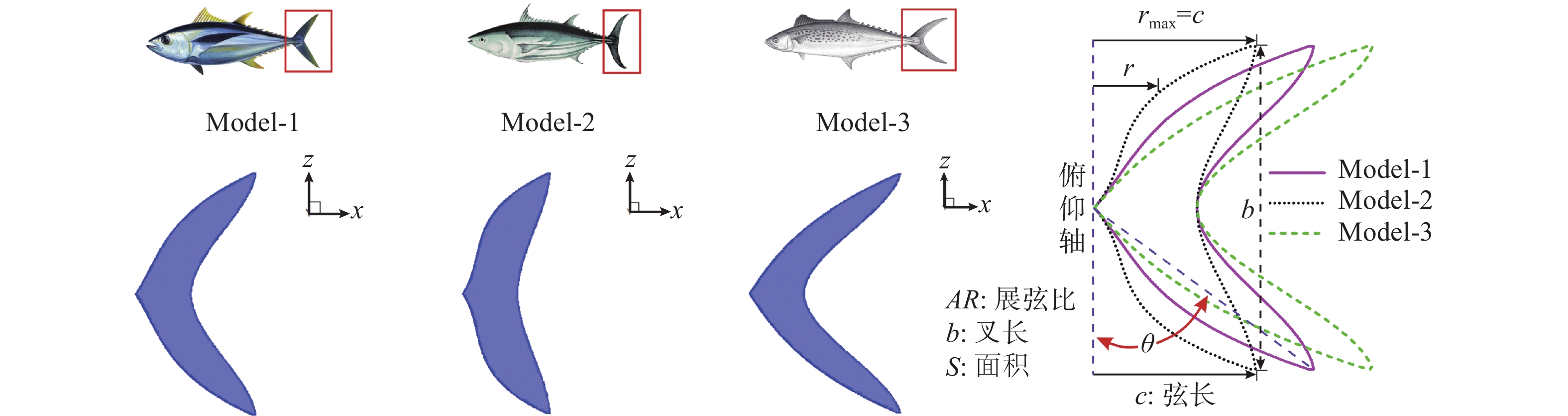
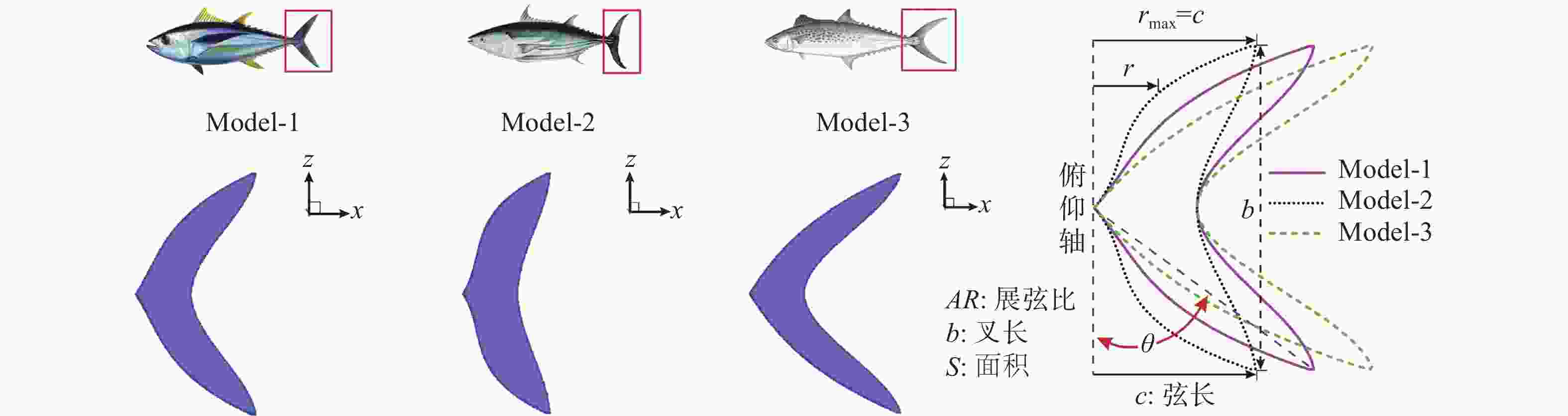
表 1 3种模型的几何参数
Table 1. Geometric parameters of the three models
模型 rmax/m Ω θ/(º) S/m2 Sr2 Sr3 1 0.100 0 5.482 45.0 7.299×10−3 0.071 8 0.047 5 2 0.073 4 5.482 36.3 7.297×10−3 0.077 7 0.051 8 3 0.126 7 5.482 51.7 7.297×10−3 0.068 9 0.045 9 
下载: 导出CSV
-
[1] Zhu D, Zhang C, Liu P, et al. Comparison of the morphology, structures and mechanical properties of teleost fish scales collected from New Zealand[J]. Journal of Bionic Engineering, 2019, 16(2): 328-336. doi: 10.1007/s42235-019-0028-1 [2] Salazar R, Fuentes V, Abdelkefi A. Classification of biological and bioinspired aquatic systems: A review[J]. Ocean Engineering, 2018, 148: 75-114. doi: 10.1016/j.oceaneng.2017.11.012 [3] Yu, J Z, Wang M, Dong H, et al. Motion control and motion coordination of bionic robotic fish: A review[J]. Journal of Bionic Engineering, 2018, 15(4): 579-598. doi: 10.1007/s42235-018-0048-2 [4] Park J W, Ryu J, Sung H J. Effects of the shape of an inverted flag on its flapping dynamics[J]. Physics of Fluids, 2019, 31(2): 021904. doi: 10.1063/1.5079579 [5] Han J, Zhang Y, Chen G. Effects of individual horizontal distance on the three-dimensional bionic flapping multi-wings in different schooling configurations[J]. Physics of Fluids, 2019, 31(4): 041903. doi: 10.1063/1.5087624 [6] Webb P W. Simple physical principles and vertebrate aquatic locomotion[J]. American Zoologist, 1988, 28(2): 709-725. doi: 10.1093/icb/28.2.709 [7] Low K H, Chong C W. Parametric study of the swimming performance of a fish robot propelled by a flexible caudal fin[J]. Bioinspiration & Biomimetics, 2010, 5(4): 046002. [8] Geder J D, Ramamurti R, Dan E, et al. Development of a robotic fin for hydrodynamic propulsion and aerodynamic control[C]//2014 Oceans-St. John’s. St. John’s, N L, Canada: IEEE, 2014. [9] Borazjani I, Daghooghi M. The fish tail motion forms an attached leading edge vortex[J]. Proceedings of the Royal Society B: Biological Sciences, 2013, 280(1756): 20122071. doi: 10.1098/rspb.2012.2071 [10] Krishnadas A, Ravichandran S, Rajagopal P. Analysis of biomimetic caudal fin shapes for optimal propulsive efficiency[J]. Ocean Engineering, 2018, 153: 132-142. doi: 10.1016/j.oceaneng.2018.01.082 [11] Xiong Z Y, Liu X M. Numerical investigation on evolutionary characteristics of the leading-edge vortex induced by flapping caudal fin[J]. Physics of Fluids, 2019, 31(12): 125117. doi: 10.1063/1.5128701 [12] Feng Y K, Su Y M, Liu H X, et al. The effects of caudal fin deformation on the hydrodynamics of thunniform swimming under self-propulsion[J]. Journal of Hydrodynamics, 2020, 32(6): 1122-1137. [13] Matta A, Pendar H, Battaglia F, et al. Impact of caudal fin shape on thrust production of a thunniform swimmer[J]. Journal of Bionic Engineering, 2020, 17(2): 254-269. doi: 10.1007/s42235-020-0020-9 [14] Liu P, Wang S, Liu R, et al. Effects of St and Re on propulsive performance of bionic oscillating caudal fin[J]. Ocean Engineering, 2020, 217(52): 107933. [15] Feng Y K, Liu H X, Su Y Y, et al. Numerical study on the hydrodynamics of C-turn maneuvering of a tuna-like fish body under self-propulsion[J]. Journal of Fluids and Structures, 2020, 94(18): 102954. [16] Zhang L, Chang X, Duan X, et al. Applications of dynamic hybrid grid method for three-dimensional moving/deforming boundary problems[J]. Computers & Fluids, 2012, 62: 45-63. [17] Seo J H, Mittal R. A sharp-interface immersed boundary method with improved mass conservation and reduced spurious pressure oscillations[J]. Journal of Computational Physics, 2011, 230(19): 7347-7363. doi: 10.1016/j.jcp.2011.06.003 -
点击查看大图
计量
- 文章访问数: 189
- HTML全文浏览量: 59
- PDF下载量: 28
- 被引次数: 0
