Adaptive Neural Network-Based Prescribed Performance Control of AUVs with Input Saturation
-
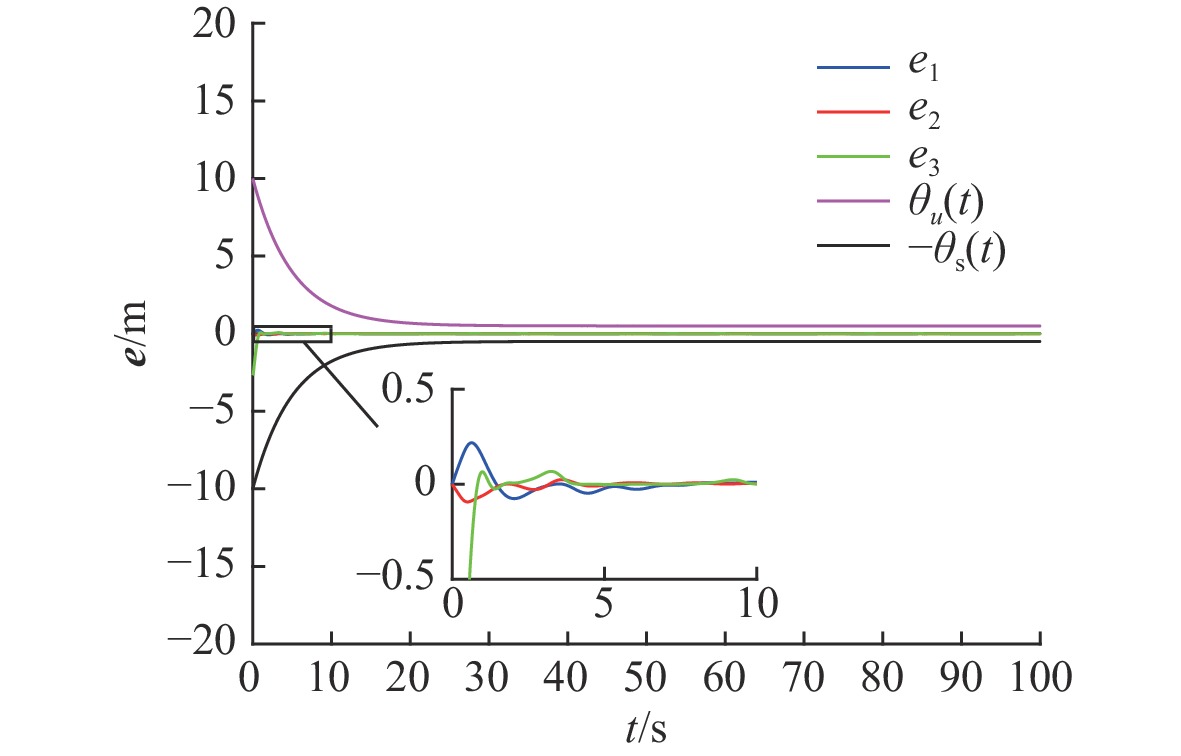
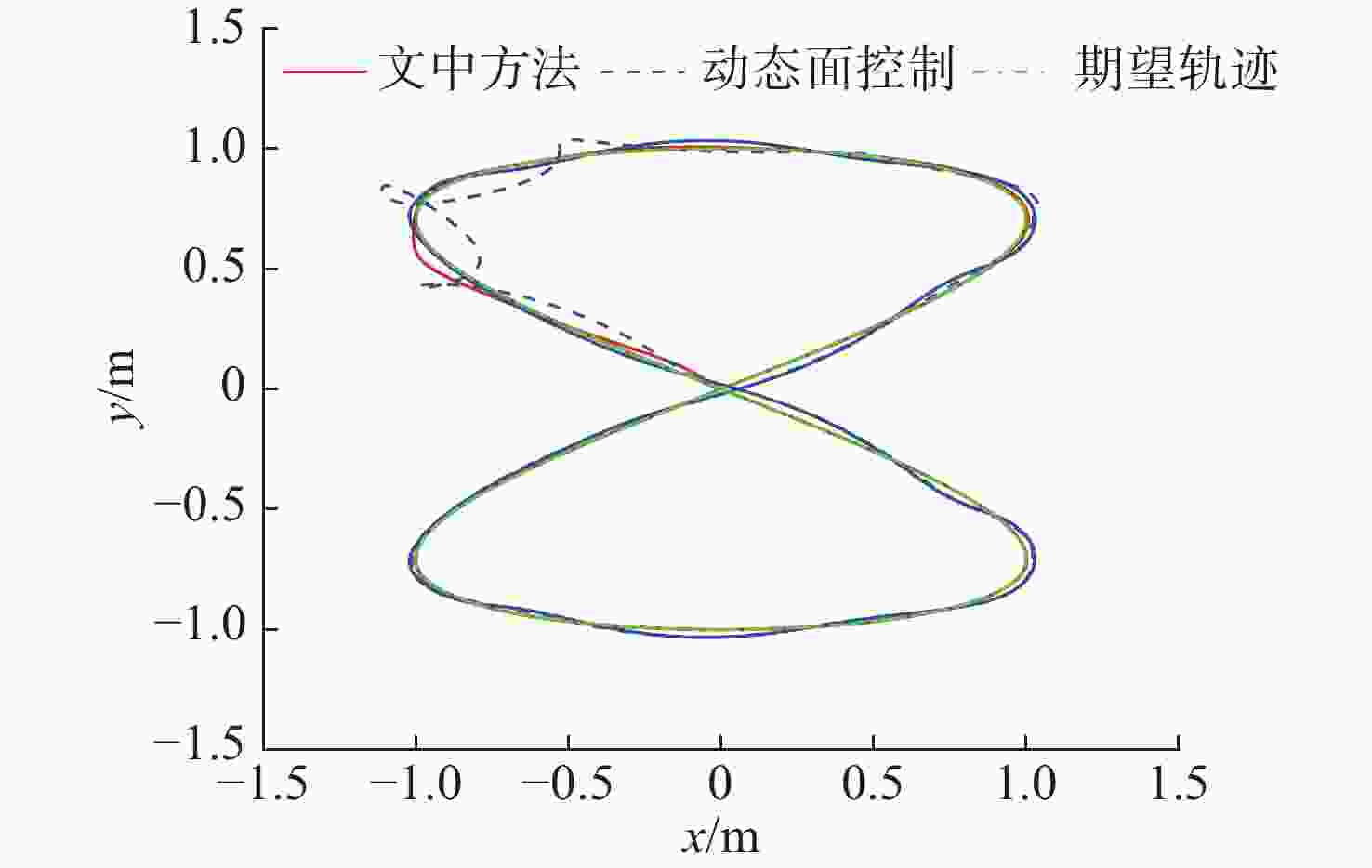
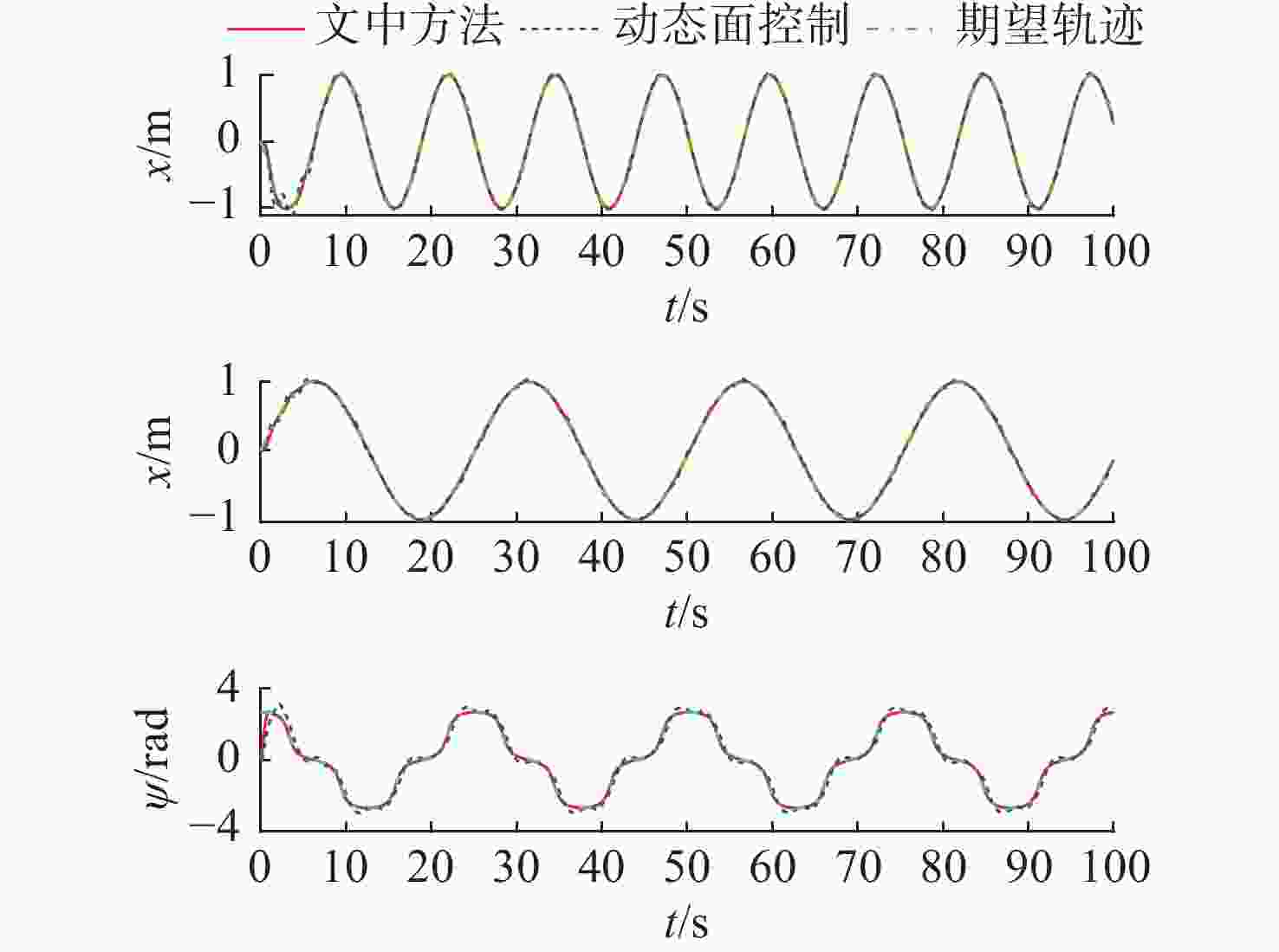
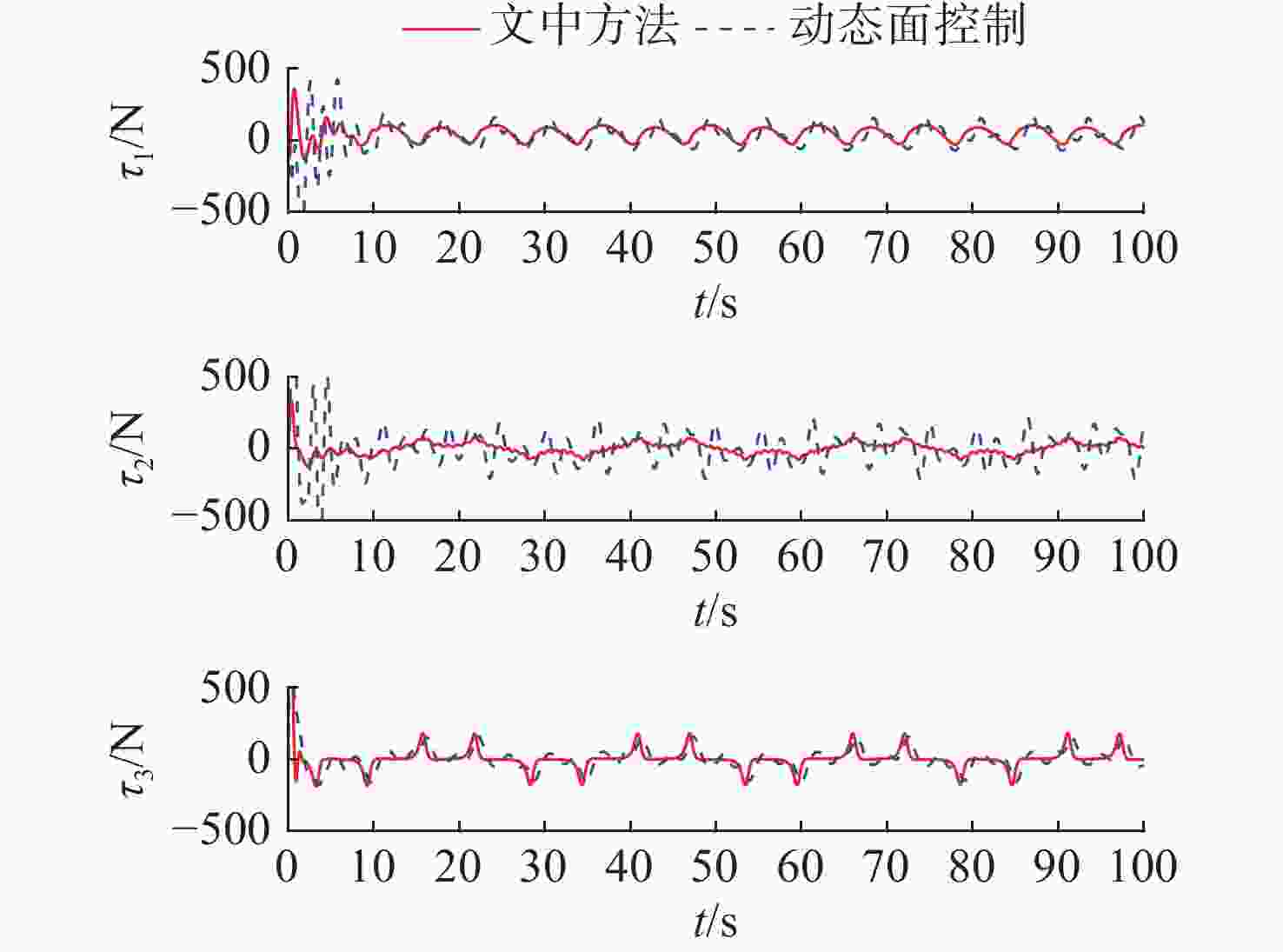
摘要: 针对自主水下航行器(AUV)系统不确定性及输入饱和问题, 提出了一种改进的自适应神经网络预设性能控制策略, 完成对期望轨迹的跟踪。首先, 引入非线性变换, 使位置误差始终处在预设时变范围内, 提高了控制精度, 并基于反步法和Lyapunov函数设计系统虚拟控制律; 然后, 利用神经网络技术处理系统模型未知参数, 并重构系统真实控制律, 使传统反步控制策略得以简化, 有效降低了计算复杂度, 并在Lyapunov稳定性理论的基础上, 证明了AUV系统的误差信号均有界; 最后, 与传统动态面控制方法进行对比, 仿真结果表明所提出的控制策略控制性能更好, 在考虑输入饱和情况下可有效克服不确定性对系统性能的影响, 实现对目标轨迹的有效跟踪。Abstract: In view of system uncertainty and input saturation of autonomous undersea vehicles(AUVs), an improved adaptive neural network-based prescribed performance control strategy was proposed to track the desired trajectory. Firstly, the nonlinear transformation was introduced to ensure that the position error remained within the preset time-varying range, improving control accuracy. Based on backstepping and Lyapunov functions, a virtual control law for the system was designed. Then, the neural network technology was used to process the unknown parameters of the system model, and the real control law of the system was reconstructed, which simplified the traditional backstepping control strategy and effectively reduced the computational complexity. Then, based on the Lyapunov stability theory, all the error signals of the AUV system were confirmed to be bounded. Finally, compared with traditional dynamic surface control methods, the simulation results show that the proposed control strategy has better control performance and can effectively overcome the impact of uncertainty on system performance by considering input saturation, effectively tracking target trajectories.
-
Key words:
- autonomous undersea vehicle /
- neural network /
- backstepping control /
- trajectory tracking
-
图 6 20%模型误差下AUV在xoy平面运行轨迹
Figure 6. The AUV running trajectory in the xoy plane at 20% model errors
图 7 20%模型误差下AUV位置跟踪曲线
Figure 7. Position tracking curves of the AUV at 20% model errors
图 8 20%模型误差下AUV执行器力矩曲线
Figure 8. Actuator torque curves of the AUV at 20% model errors
表 1 模型参数
Table 1. Model parameters
参数 数值 参数 数值 $ {m / {{\text{kg}}}} $ 116.0 $ {{{N_r}} / {({{{\text{kg}} \cdot {\text{m}}} \mathord{\left/ {\vphantom {{{\text{kg}} \cdot {\text{m}}} {\text{s}}}} \right. } {\text{s}}})}} $ 3.5 $ {{{I_z}} / {({\text{kg}} \cdot {{\text{m}}^2})}} $ 13.1 $ {{{D_u}} / {({{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\text{m}}}} \right. } {\text{m}}})}} $ 241.3 $ {{{X_{\dot u}}} / {{\text{kg}}}} $ −167.6 $ {{{D_v}} / {({{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\text{m}}}} \right. } {\text{m}}})}} $ 503.8 $ {{{Y_{\dot v}}} / {{\text{kg}}}} $ −477.2 $ {{{D_r}} / {({{{\text{kg}} \cdot {\text{m}}} \mathord{\left/ {\vphantom {{{\text{kg}} \cdot {\text{m}}} {\text{s}}}} \right. } {\text{s}}})}} $ 76.9 $ {{{N_{\dot r}}} / {{\text{kg}}}} $ −15.9 $ {{{M_{\dot u}}} / {{\rm{kg}}}} $ 283.6 $ {{{X_u}} / {({{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {\text{s}}}} \right. } {\text{s}}})}} $ 26.9 $ {{{M_{\dot v}}} / {{\rm{kg}}}} $ 593.2 $ {Y}_{v}/(\text{kg}/\text{s}) $ 35.8 $ {{{M_{\dot r}}} /{{\rm{kg}}}} $ 29.0 
下载: 导出CSV
表 2 各方向均方误差对比
Table 2. Comparison of the meansquare error in different directions
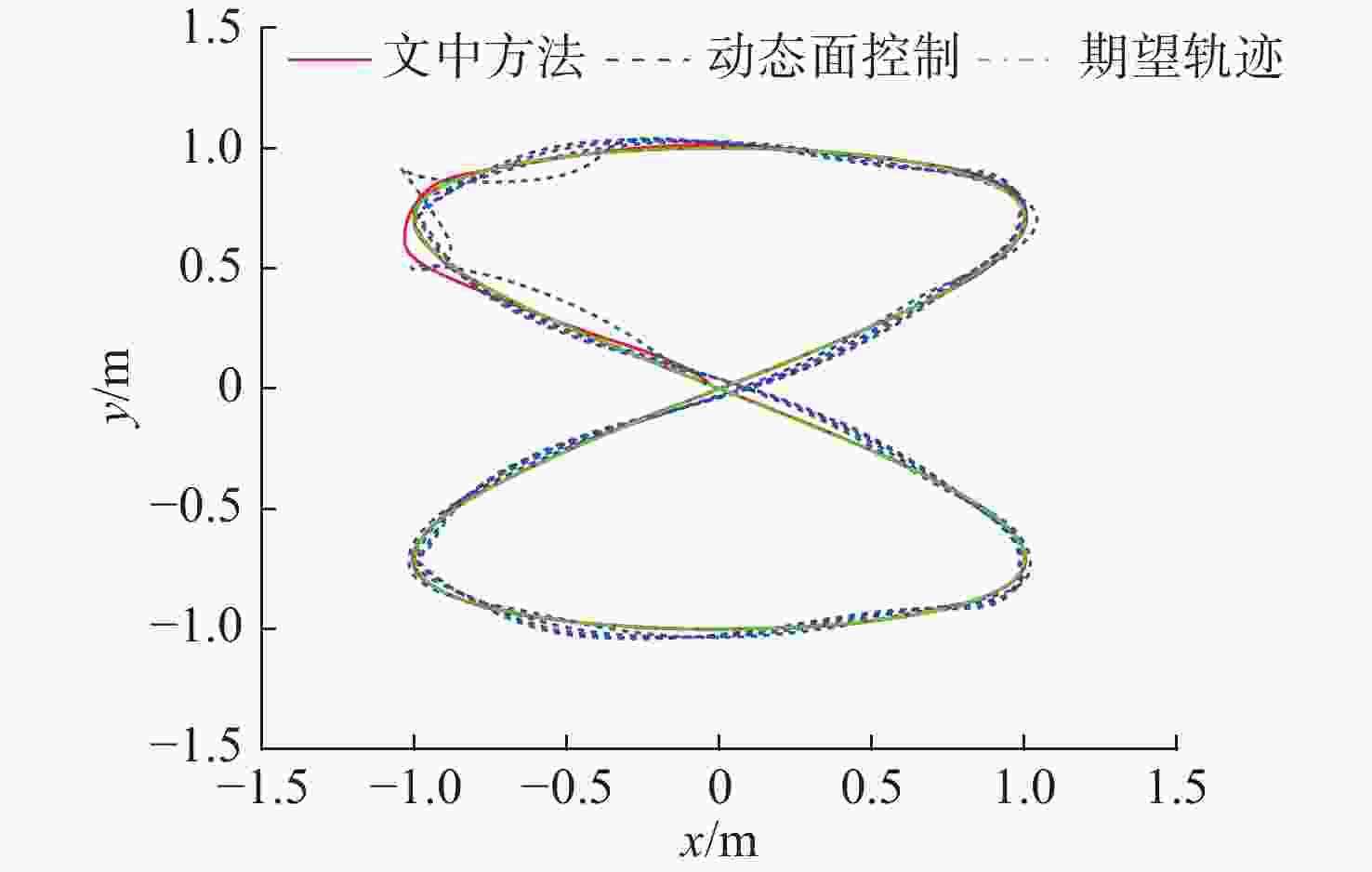
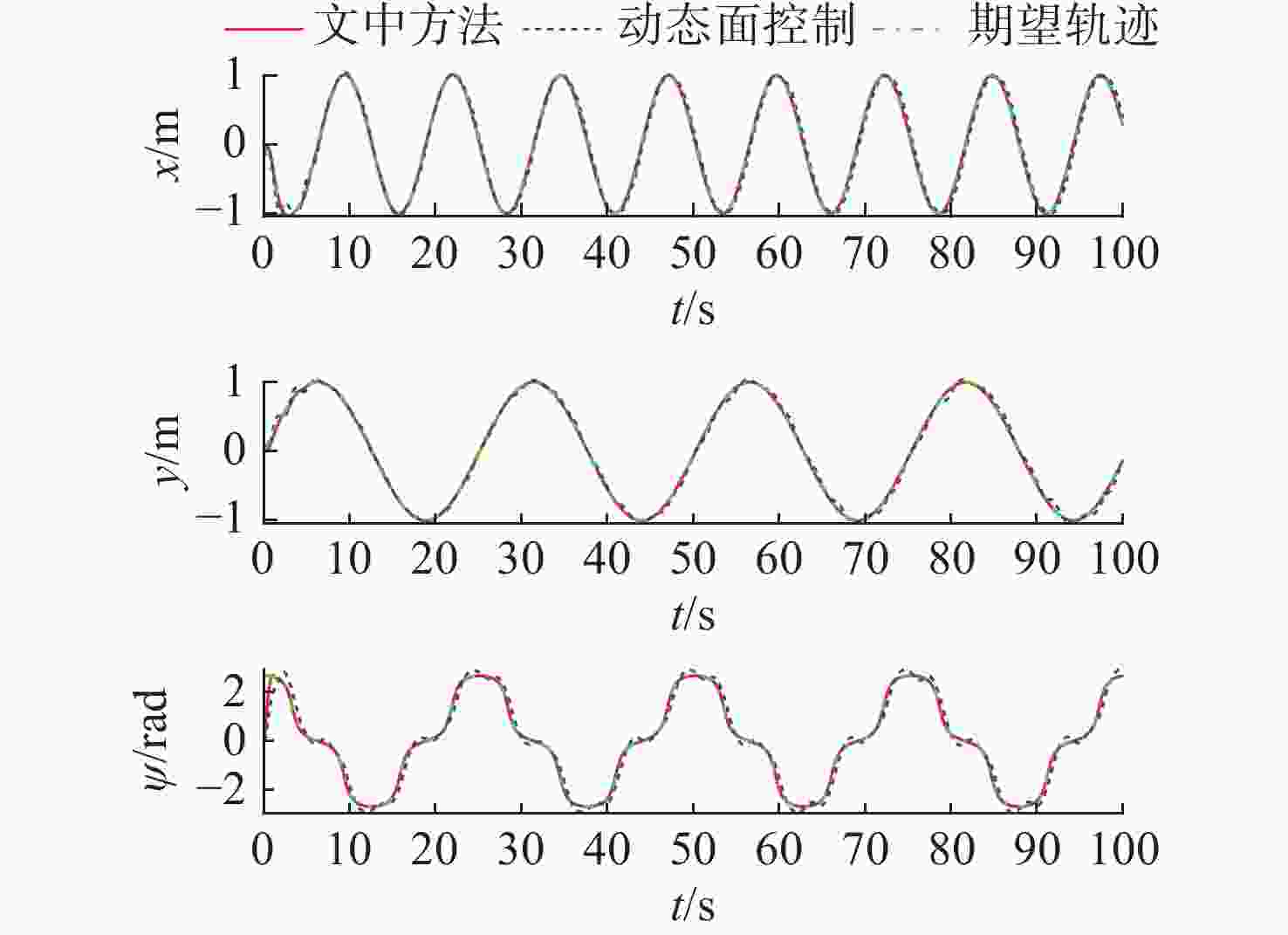
参数 xmse/m2 ymse/m2 $ {\psi_{\rm{mse}}} $/rad2 文中方法 0.000 3 0.000 1 0.021 4 动态面控制 0.005 1 0.002 0 0.082 1
下载: 导出CSV
-
[1] Wu Z, Wang Q, Huang H. Adaptive neural networks trajectory tracking control for autonomous underwater helicopters with prescribed performance[J]. Ocean Engineering, 2022, 264: 112519. doi: 10.1016/j.oceaneng.2022.112519 [2] Cui J, Zhao L, Yu J, et al. Neural network-based adaptive finite-time consensus tracking control for multiple autonomous underwater vehicles[J]. IEEE Access, 2019, 7: 33064-33074. doi: 10.1109/ACCESS.2019.2903833 [3] Shojaei K. Neural network feedback linearization target tracking control of underactuated autonomous underwater vehicles with a guaranteed performance[J]. Ocean Engineering, 2022, 258: 111827. doi: 10.1016/j.oceaneng.2022.111827 [4] Yang C, Yao F, Zhang M J. Adaptive backstepping terminal sliding mode control method based on recurrent neural networks for autonomous underwater vehicle[J]. Chinese Journal of Mechanical Engineering, 2018, 31(1): 1-16. doi: 10.1186/s10033-018-0219-4 [5] Gong P, Yan Z, Zhang W, et al. Trajectory tracking control for autonomous underwater vehicles based on dual closed-loop of MPC with uncertain dynamics[J]. Ocean Engineering, 2022, 265: 112697. doi: 10.1016/j.oceaneng.2022.112697 [6] Cao J, Sun Y, Zhang G, et al. Target tracking control of underactuated autonomous underwater vehicle based on adaptive nonsingular terminal sliding mode control[J]. International Journal of Advanced Robotic Systems, 2020, 17(2): 451-468. [7] Guo L, Liu W, Li L, et al. Neural network non-singular terminal sliding mode control for target tracking of underactuated underwater robots with prescribed performance[J]. Journal of Marine Science and Engineering, 2022, 10(2): 252. doi: 10.3390/jmse10020252 [8] Xia Y, Xu K, Huang Z, et al. Adaptive energy-efficient tracking control of a X rudder AUV with actuator dynamics and rolling restriction[J]. Applied Ocean Research, 2022, 118: 102994. doi: 10.1016/j.apor.2021.102994 [9] Fang Y, Huang Z, Pu J, et al. AUV position tracking and trajectory control based on fast-deployed deep reinforcement learning method[J]. Ocean Engineering, 2022, 245: 110452. doi: 10.1016/j.oceaneng.2021.110452 [10] 赵杰梅, 胡忠辉. 基于动态反馈的AUV水平面路径跟踪控制[J]. 浙江大学学报: 工学版, 2018, 52(8): 1467-1473, 1481.Zhao Jiemei, Hu Zhonghui. Path following control of AUV in horizontal plane based on dynamic feedback control[J]. Journal of Zhejiang University(Engineering Science), 2018, 52(8): 1467-1473, 1481. [11] 杨超, 郭佳, 张铭钧. 基于RBF神经网络的作业型 AUV 自适应终端滑模控制方法及实验研究[J]. 机器人, 2018, 40(3): 336-345.Yang Chao, Guo Jia, Zhang Mingjun. Adaptive terminal sliding mode control method based on RBF neural network for operational AUV and its experimental research[J]. Robot, 2018, 40(3): 336-345. [12] 王金强, 王聪, 魏英杰, 等. 欠驱动 AUV 自适应神经网络反步滑模跟踪控制[J]. 华中科技大学学报: 自然科学版, 2019, 47(12): 12-17.Wang Jinqiang, Wang Cong, Wei Yingjie, et al. Path following of an underactuated AUV based on adaptive neural network backstepping sliding mode control[J]. Journal of Huazhong University of Science and Technology, 2019, 47(12): 12-17. [13] 王香, 张永林. 基于 RBF 神经网络的 AUV 路径跟踪分数阶滑模控制[J]. 水下无人系统学报, 2020, 28(3): 284-290.Wang Xiang, Zhang Yonglin. Fractional-Order sliding mode control based on RBF neural network for AUV path tracking[J]. Journal of Unmanned Undersea Systems, 2020, 28(3): 284-290. [14] 霍宇彤, 郭晨, 于浩淼. 欠驱动 AUV 三维路径跟踪 RBF 神经网络积分滑模控制[J]. 水下无人系统学报, 2020, 28(2): 131-138.Huo Yutong, Guo Chen, Yu Haomiao. RBF neural network integral sliding mode control for three-dimensional path following of underactuated AUV[J]. Journal of Unmanned Undersea Systems, 2020, 28(2): 131-138. [15] 胡汇源, 毛骏. 具有未建模动态和输入饱和约束的纯反馈非线性系统自适应神经网络控制[J]. 中国计量大学学报, 2021, 32(4): 539-548. doi: 10.3969/j.issn.2096-2835.2021.04.015Hu Huiyuan, Mao Jun. Adaptive neural control of pure-feedback nonlinear systems with unmodeled dynamics and input saturation[J]. Journal of China University of Metrology, 2021, 32(4): 539-548. doi: 10.3969/j.issn.2096-2835.2021.04.015 [16] von Ellenrieder K D. Dynamic surface control of trajectory tracking marine vehicles with actuator magnitude and rate limits[J]. Automatica, 2019, 105: 433-442. doi: 10.1016/j.automatica.2019.04.018 [17] Wang H, Chen B, Liu X, et al. Adaptive neural tracking control for stochastic nonlinear strict-feedback systems with unknown input saturation[J]. Information Sciences, 2014, 269: 300-315. doi: 10.1016/j.ins.2013.09.043 [18] Sun G, Wang D, Li T, et al. Single neural network approximation based adaptive control for a class of uncertain strict-feedback nonlinear systems[J]. Nonlinear dynamics, 2013, 72(1): 175-184. [19] Shen C, Shi Y, Buckham B. Trajectory tracking control of an autonomous underwater vehicle using Lyapunov-based model predictive control[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5796-5805. doi: 10.1109/TIE.2017.2779442 -
点击查看大图
图(8) / 表(2)
计量
- 文章访问数: 238
- HTML全文浏览量: 81
- PDF下载量: 40
- 被引次数: 0
