Torpedo Hit Probability Prediction Method Based on Deep Neural Network
-
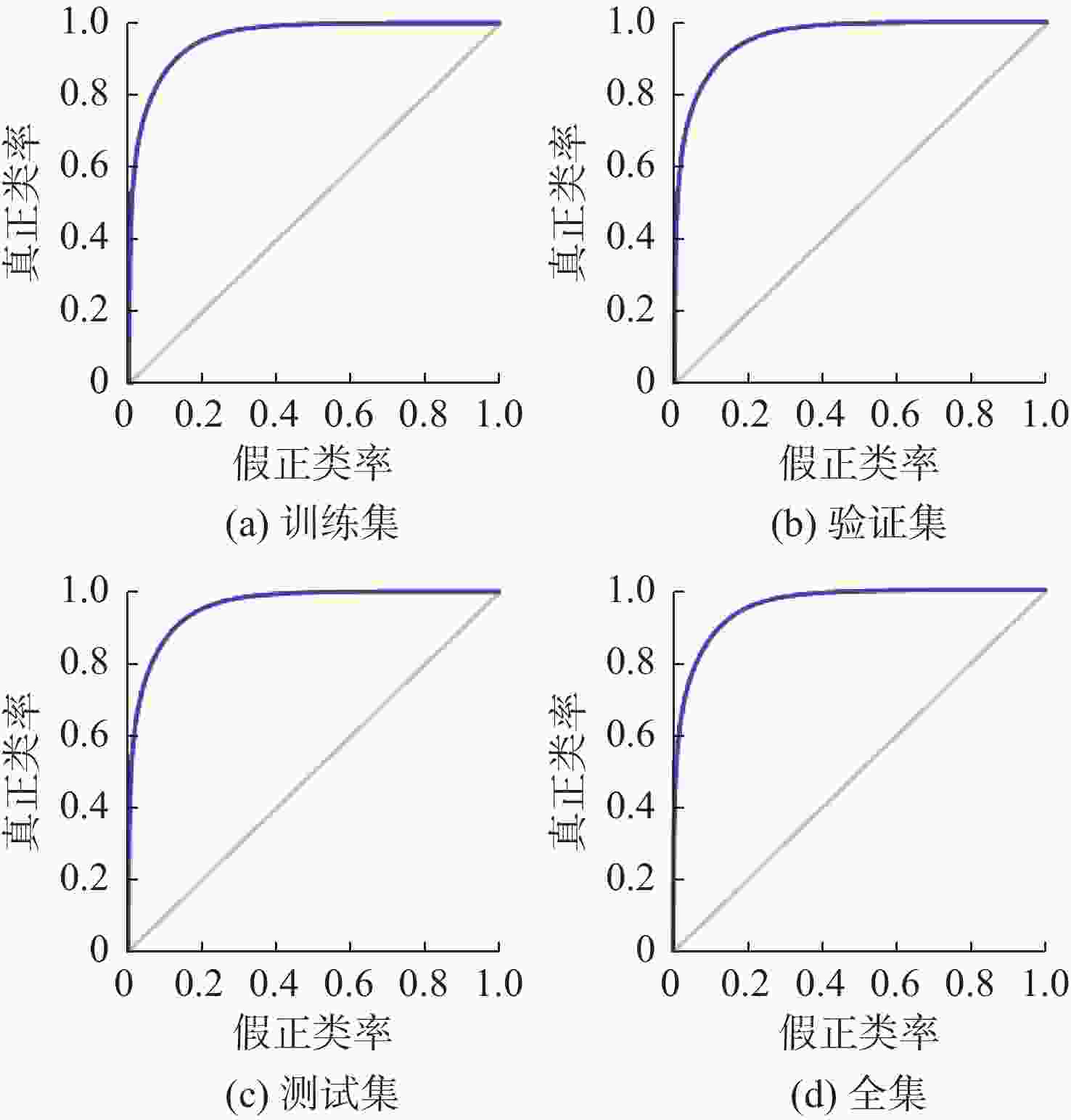
摘要: 为进一步提升鱼雷命中概率预测能力, 文中提出一种基于深度神经网络(DNN)的鱼雷命中概率预测方法。首先提取了态势特征信息, 设定了想定态势空间, 基于蒙特卡洛方法, 构建了鱼雷作战的大样本数据集; 在此基础上, 利用Levenberg-Marquardt优化算法计算最优梯度方向, 提高了算法的计算效率; 最后基于模型给出了2种典型的作战应用模式。实验结果表明, 文中提出的DNN预测模型相比其他典型智能算法识别准确率更高, 验证了模型的有效性和优越性。Abstract: In order to further improve the prediction ability of torpedo hit probability, a torpedo hit probability prediction method based on deep neural network(DNN) was proposed. Firstly, the situation characteristic information was extracted, and the desired situation space was set. In addition, the large sample data set of torpedo operation was constructed based on the Monte-Carlo method. On this basis, the Levenberg-Marquardt optimization algorithm was used to calculate the optimal gradient direction, which improved the computational efficiency of the algorithm. Finally, two typical operational application modes were given based on the model. Experimental results show that the proposed DNN-based prediction model has higher recognition accuracy than other typical intelligent algorithms, which verifies the effectiveness and superiority of the model.
-
Key words:
- torpedo /
- deep neural network /
- hit probability /
- operational effectiveness
-
图 6 训练集、验证集、测试集及数据全集混淆矩阵
Figure 6. Confusion matrix of training set, validation set, test set, and data set
图 7 训练集、验证集、测试集及数据全集ROC曲线
Figure 7. ROC curves of training set, validation set, test set, and data set
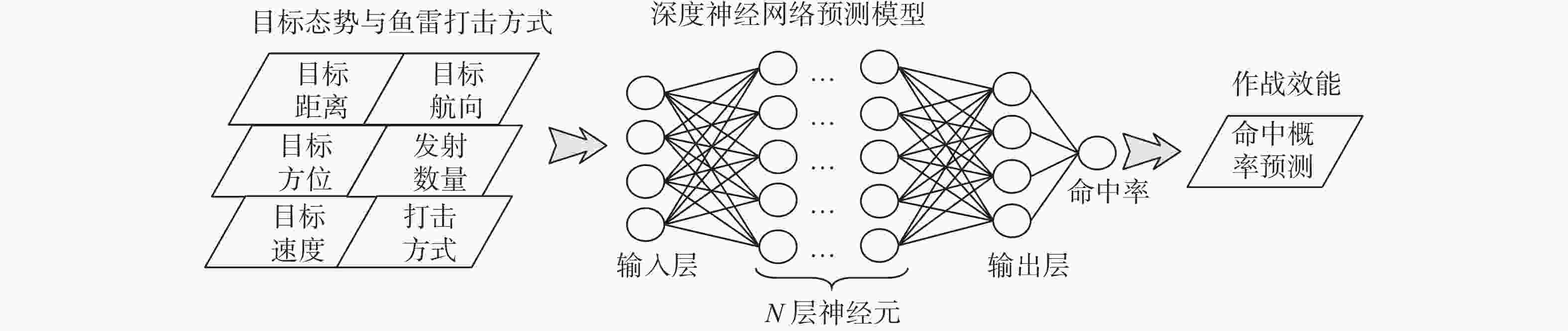
表 1 网络输入输出的状态空间
Table 1. State space of network inputs and outputs
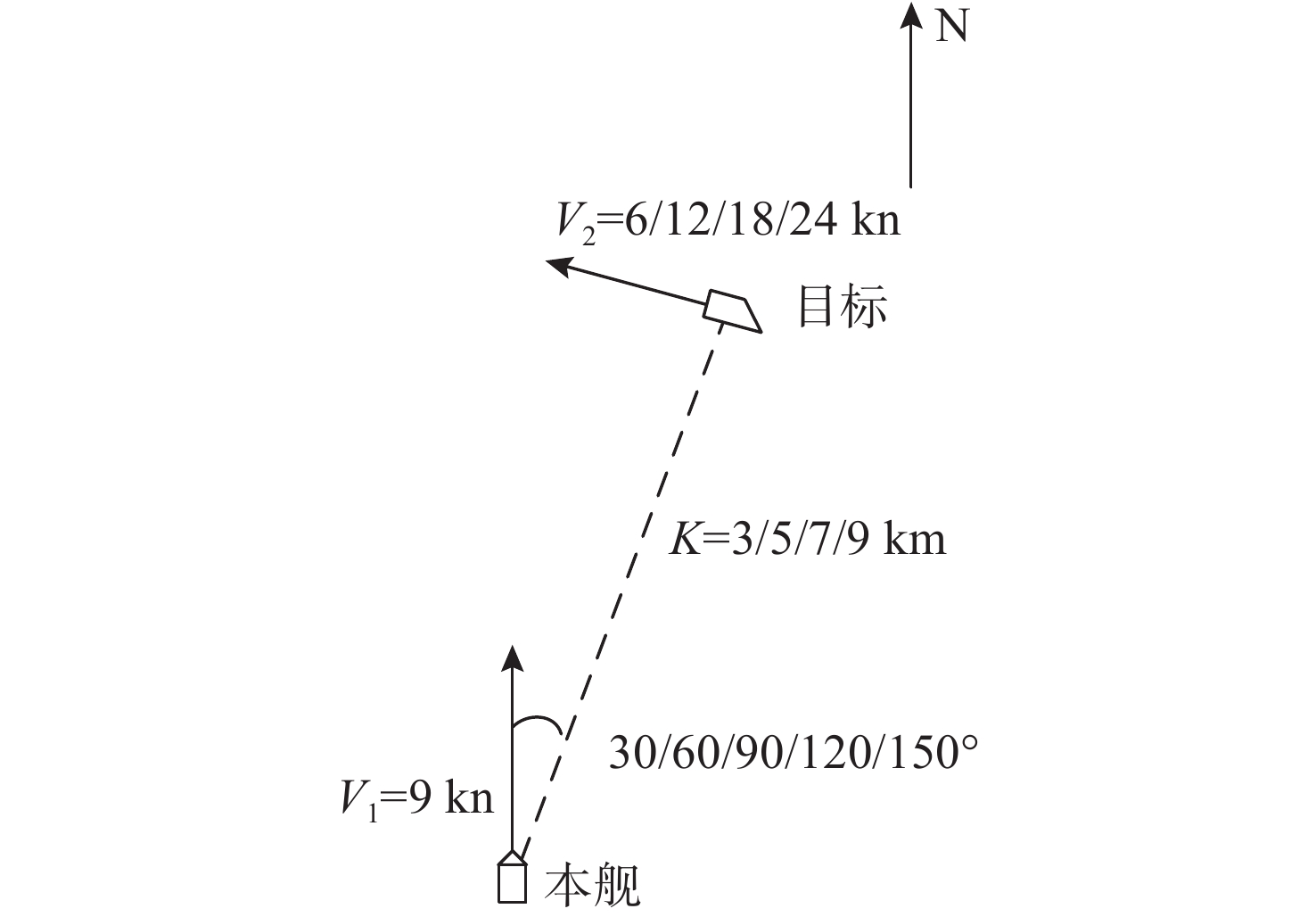
类型 参数类型 备注 目标距离 连续型输入 $[2\;500,\;9\;500\;{\text{m}}]$ 目标方位 连续型输入 $[0,2{\text{π}}]$ 目标速度 连续型输入 $[2,\;13\;{\text{m/s}}]$ 目标航向 连续型输入 $( - {\text{π}},{\text{π}}]$ 鱼雷发射数量 离散型输入 单雷、双雷齐射 鱼雷射击方法 离散型输入 现在点、提前角 鱼雷命中概率 连续型输出 $[0,1]$ 
下载: 导出CSV
表 2 DNN超参数设定
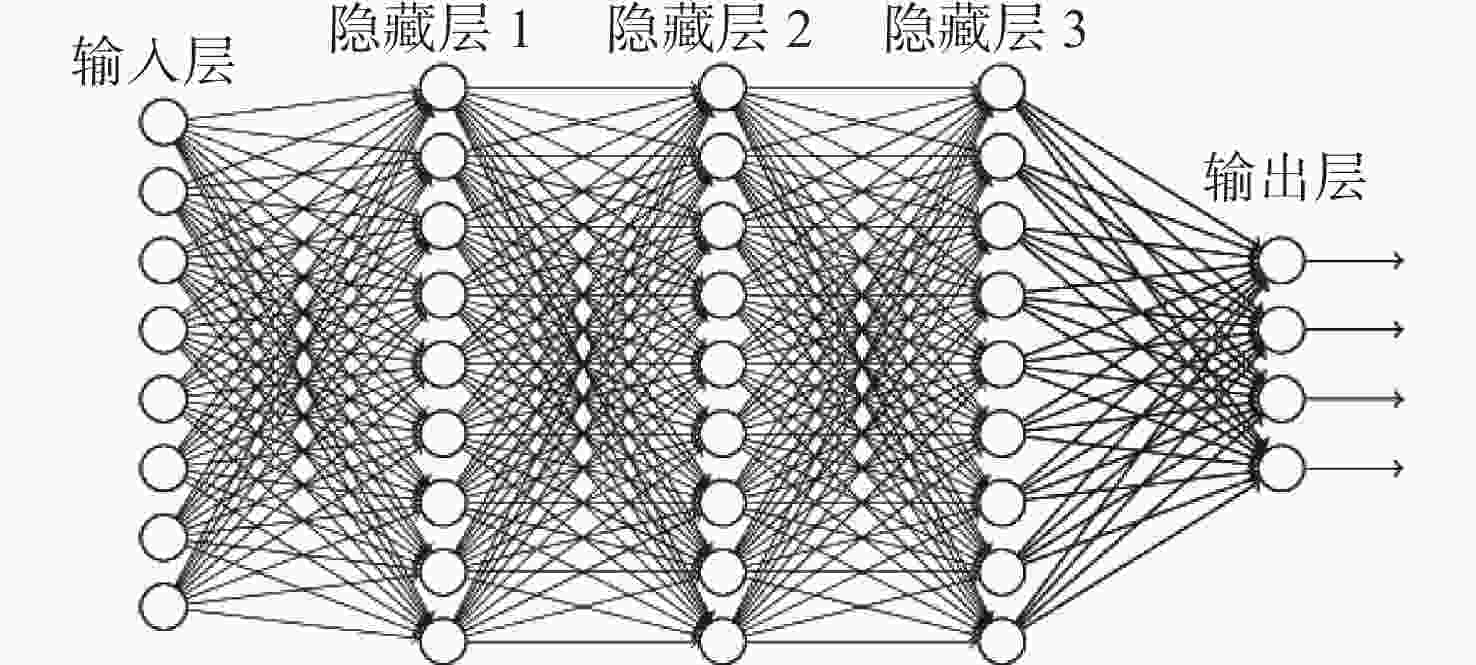
Table 2. Hyper-parameter settings of DNN
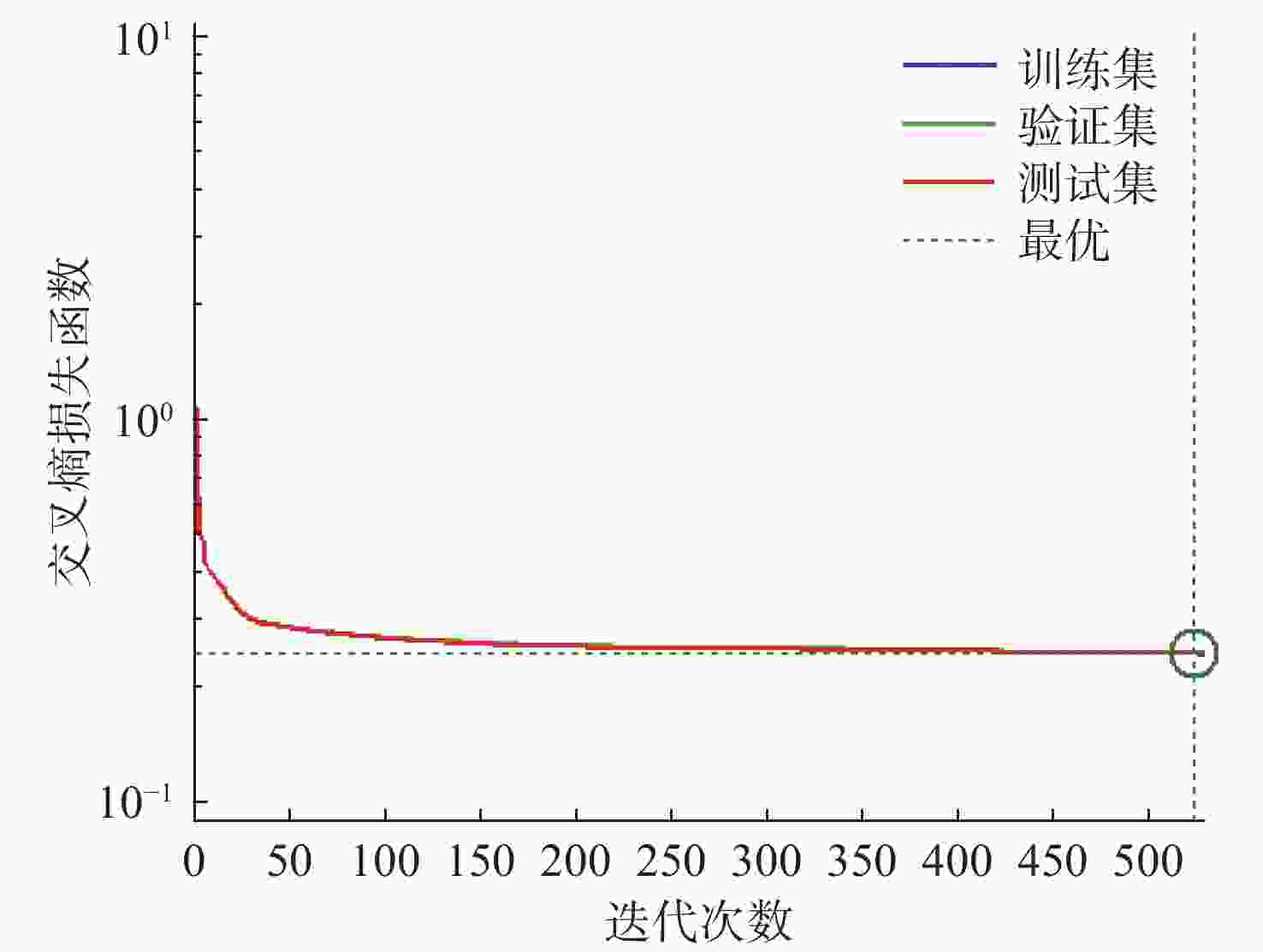
参数 取值 深度神经网络层数 35 训练次数 1 000 训练目标 0.001 学习率 0.1 激活函数 Sigmoid 寻优算法 L-M算法 损失函数 交叉熵损失函数
下载: 导出CSV
表 3 部分训练样本数据
Table 3. Partial training sample data
态势 目标距离
/m目标方位
/rad目标速度
/(m/s)目标航向/rad 鱼雷发射
数量鱼雷射击方法 仿真结果 1 2 999.53 −0.54 3.11 5.91 单雷 现在点 命中 2 2 762.44 −0.65 2.74 6.11 单雷 现在点 命中 3 7 012.4 −2.11 9.58 0.36 单雷 现在点 未命中 4 3 052.61 −2.52 6.00 6.14 单雷 有利提前角 命中 5 7 084.06 −0.80 3.93 1.61 单雷 有利提前角 命中 6 2 873.67 −0.60 5.30 0.62 双雷齐射 现在点 命中 7 7 047.18 −2.11 −0.48 4.05 双雷齐射 现在点 命中 8 5 071.11 −2.37 13.43 4.85 双雷齐射 现在点 未命中 9 5 008.33 −0.93 4.57 4.58 双雷齐射 有利提前角 命中 10 2 894.14 −1.11 8.71 1.43 双雷齐射 有利提前角 命中
下载: 导出CSV
表 4 其他机器学习方法统计结果
Table 4. Statistical results of other machine learning methods
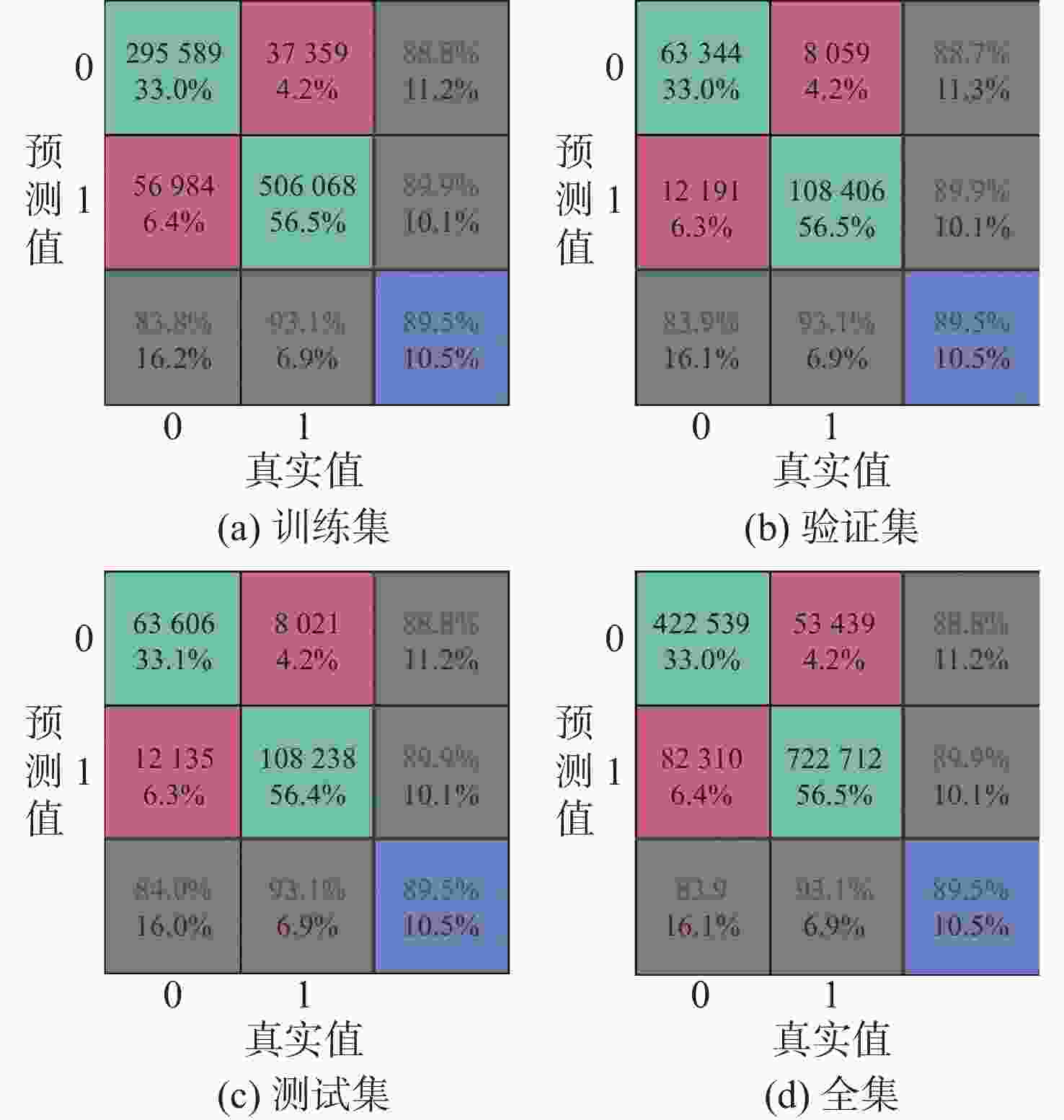
方法 预测成功率/% 二叉树算法 87.3 二次判别分析算法 80.3 逻辑回归算法 81.3 K近邻算法 86.9 BP神经网络算法 85.5
下载: 导出CSV
-
[1] 武志东, 于雪泳, 许兆鹏. 潜射鱼雷命中概率的解析计算通式及应用[J]. 水下无人系统学报, 2021, 29(2): 203-209.Wu Zhidong, Yu Xueyong, Xu Zhaopeng. Analytic formula and employment of the hitting probability for sub-launched torpedo[J]. Journal of Unmanned Undersea Systems, 2021, 29(2): 203-209. [2] 丁光强. 一种火箭助飞鱼雷命中概率实时评估模型[J]. 海军航空工程学院学报, 2015(2): 147-150.Ding Guangqiang. A real-time evaluating model of RAT’s hit probability[J]. Journal of Naval Aviation University, 2015(2): 147-150. [3] 谢超, 周景军, 万亚民, 等. 基于脱靶量散布的超空泡鱼雷命中概率研究[J]. 水下无人系统学报, 2022, 30(2): 237-244, 253.Xie Chao, Zhou Jingjun, Wan Yamin, et al. Research on hitting probability of supercavitating torpedo based on dispersion of miss distance[J]. Journal of Unmanned Undersea Systems, 2022, 30(2): 237-244, 253. [4] 吴宝奇, 关晓存, 石敬斌. 电磁线圈发射舰载反鱼雷鱼雷拦截概率仿真分析[J]. 火炮发射与控制学报, 2021, 42(4): 7-12.Wu Baoqi, Guan Xiaocun, Shi Jingbin. Intercept probability simulation and analysis of electromagnetic coil launched anti-torpedo torpedo[J]. Journal of Gun Launch & Control, 2021, 42(4): 7-12. [5] 袁富宇, 代志恒, 肖碧琴. 基于误差折算的鱼雷一次转角射击命中/发现概率解析计算方法[J]. 水下无人系统学报, 2020, 28(3): 303-308.Yuan Fuyu, Dai Zhiheng, Xiao Biqin. An analytical calculation mothed of the hitting/finding probability of torpedo one-time turning-angle shooting based on error conversion[J]. Journal of Unmanned Undersea Systems, 2020, 28(3): 303-308. [6] 杜毅, 黄文斌, 彭汉国. 基于贝叶斯网络的潜艇攻击决策研究[J]. 火力与指挥控制, 2009, 34(S1): 37-40.Du Yi, Huang Wenbin, Peng Hanguo. Research on submarine attack decision based on bayesian network[J]. Fire Control & Command Control, 2009, 34(S1): 37-40. [7] 唐克, 王存威, 卢金星. 基于神经网络和matlab的末敏弹系统效能灵敏度仿真[J]. 兵工自动化, 2010, 29(7): 90-93.Tang Ke, Wang Cunwei, Lu Jinxing. Research of factor of influencing shrapnel spreading precision based on neural network and Matlab[J]. Ordnance Industry Automation, 2010, 29(7): 90-93. [8] 朱虎明, 李佩, 焦李成, 等. 深度神经网络并行化综述[J]. 计算机学报, 2018, 41(8): 1861-1881.Zhu Huming, Li Pei, Jiao Licheng, et al. Review of parallel deep neural network, 2018, 41(8): 1861-1881. [9] 任进军, 王宁. 人工神经网络中损失函数的研究[J]. 甘肃高师学报, 2018, 23(2): 61-63.Ren Jinjun, Wang Ning. Research on cost function in artificial neural network[J]. Journal of Gansu Normal Colleges, 2018, 23(2): 61-63. [10] 赵弘, 周瑞祥, 林廷圻. 基于Levenberg-Marquardt算法的神经网络监督控制[J]. 西安交通大学学报, 2002, 36(5): 523-527.Zhao Hong, Zhou Ruixiang, Lin Tingqi. Neural network supervised control based on levenberg-marquardt algorithm[J]. Journal of Xi’an Jiaotong University, 2002, 36(5): 523-527. -
点击查看大图
计量
- 文章访问数: 252
- HTML全文浏览量: 23
- PDF下载量: 53
- 被引次数: 0
