ESO-Based Robust Model Predictive Control for Undersea Vehicle Manipulator System
-
摘要: 考虑到海洋环境的复杂性、不确定性及水下机器人机械臂系统(UVMS)的强非线性、强耦合性等特点, 提出一种基于扩张状态观测器(ESO)的鲁棒模型预测控制(RMPC)方法。首先基于UVMS的动力学特性, 建立其动力学模型, 并忽略不确定项和干扰给出其名义模型系统。然后, 基于名义系统设计了RMPC算法。将原系统的不确定项、干扰以及建模误差等影响因素集总为扩张状态, 设计了ESO对其进行估计, 并在名义模型的RMPC基础上进行了补偿, 以得到应用于UVMS系统的RMPC方法。最后通过仿真实验证明, 基于ESO的RMPC具有很好的轨迹跟踪性能和抗扰动能力。
-
关键词:
- 水下机器人机械臂系统 /
- 鲁棒模型预测控制 /
- 扩张状态观测器 /
- 轨迹跟踪
Abstract: In view of the complexity and uncertainty of the marine environment and the strong nonlinearity and coupling of the undersea vehicle manipulator system(UVMS), this paper proposed a robust model predictive control(RMPC) method based on extended state observer(ESO). First, a dynamics model was established based on the dynamics characteristics of UVMS, and a nominal model system was defined by ignoring uncertainties and disturbances. Then, a UVMS algorithm was designed for the nominal system. The uncertainties, disturbances, modeling errors, and other influencing factors of the original system were summarized into extended states, and an ESO was designed to estimate these factors. Furthermore, the factors were compensated based on the RMPC of the nominal model, so as to obtain the RMPC method applied to the UVMS system. Finally, it is demonstrated through simulation experiments that the ESO-based RMPC has good trajectory tracking performance and anti-disturbance capability. -
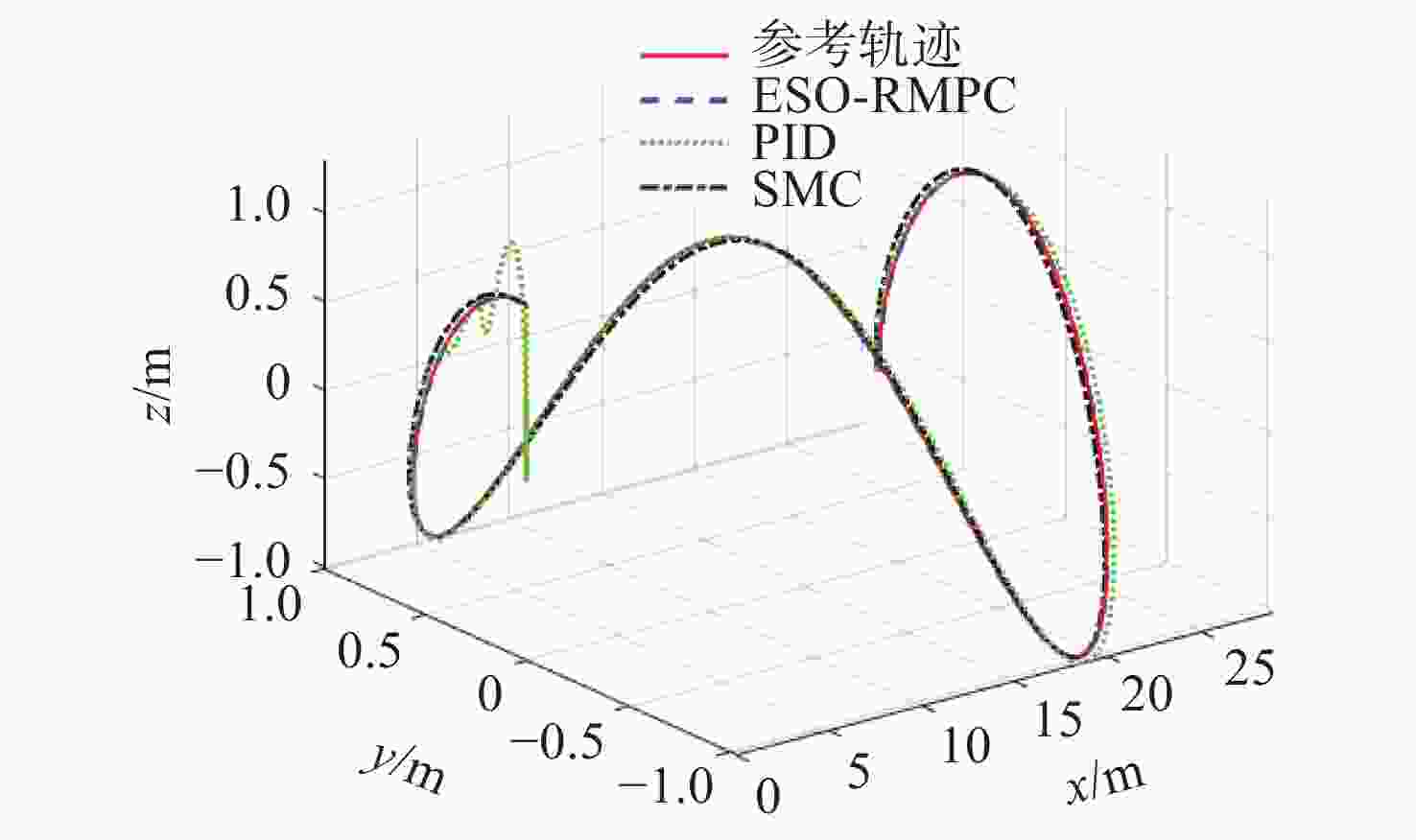
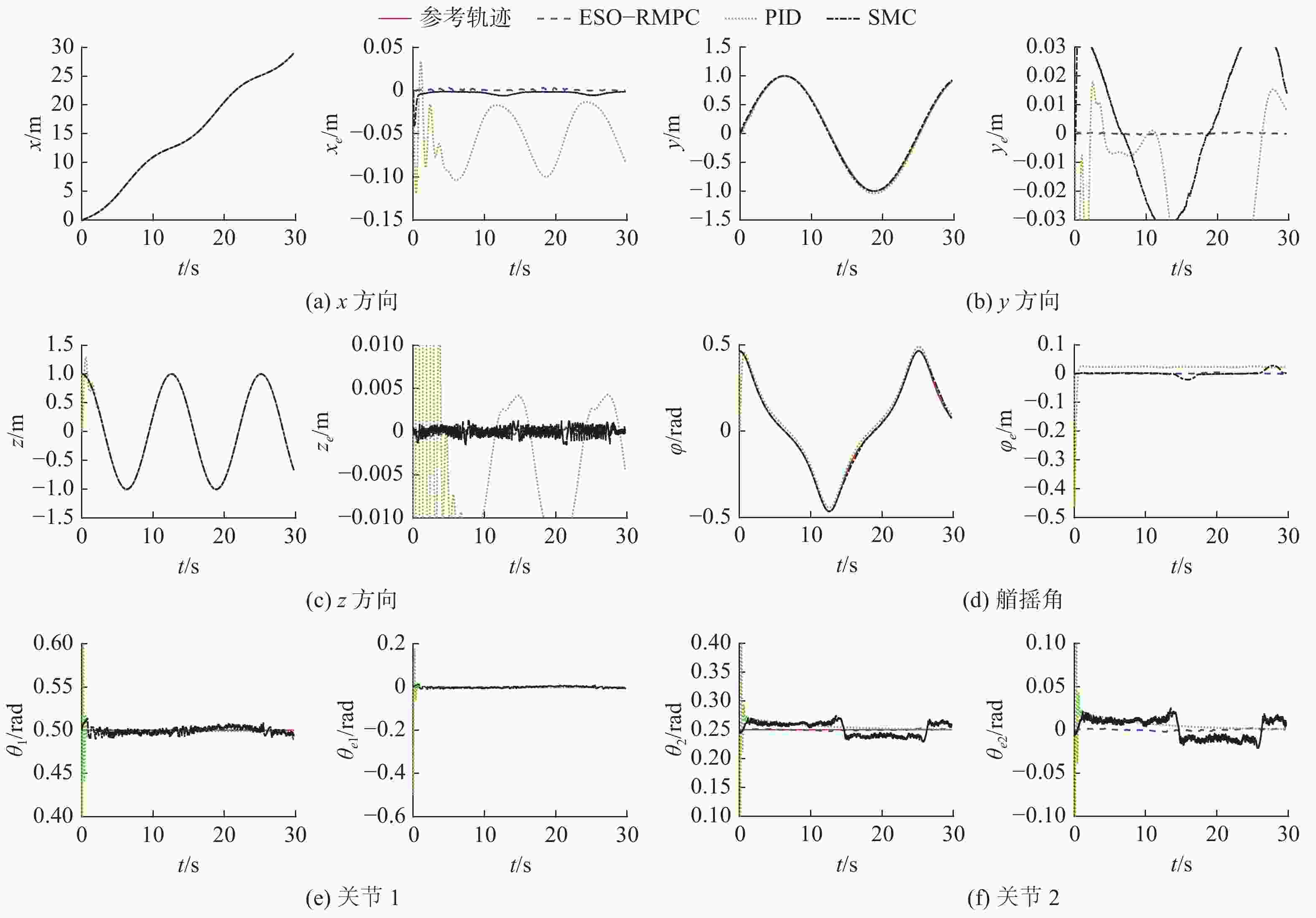
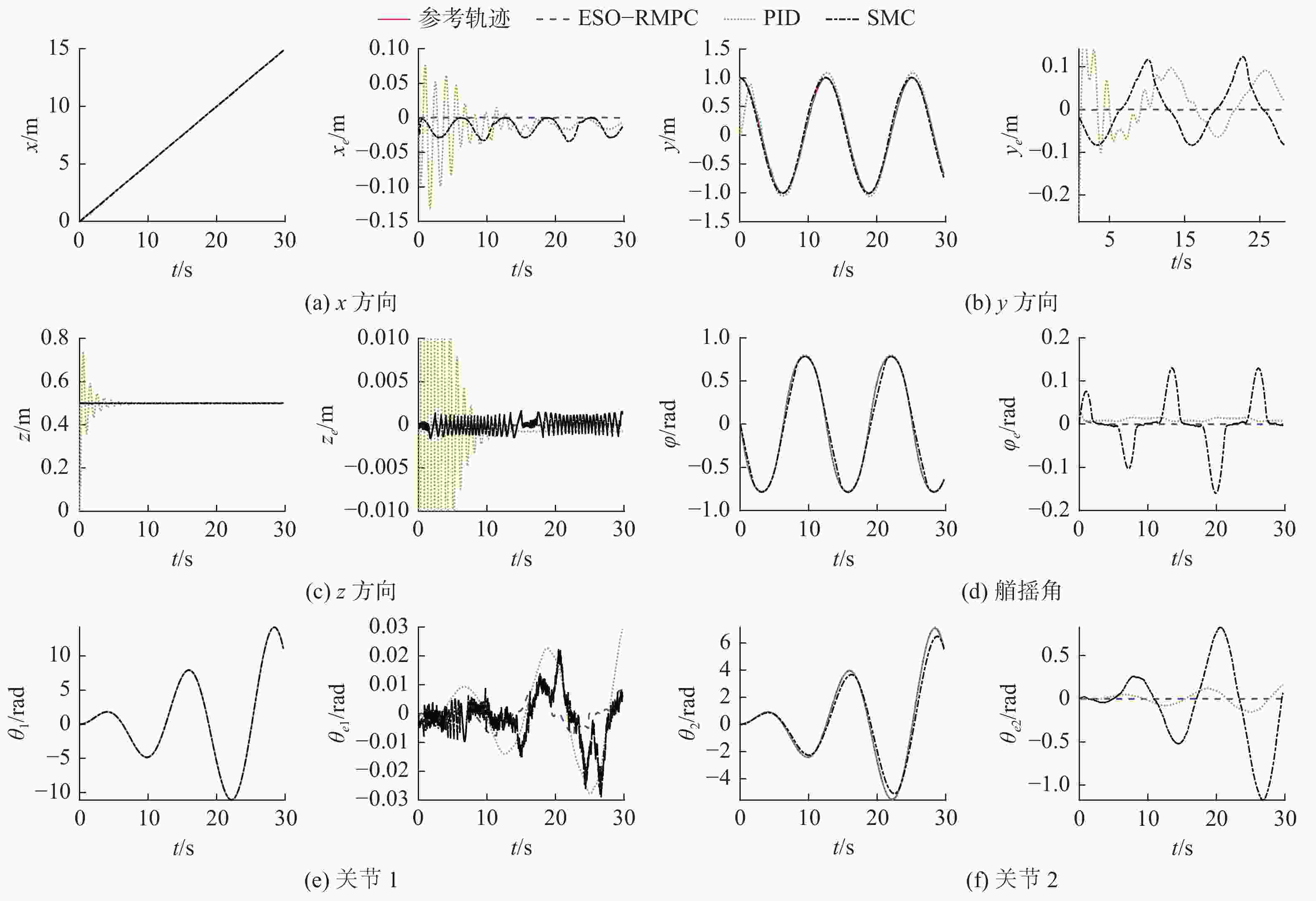
表 1 工况1下各控制器的跟踪误差RMS指标
Table 1. The tracking error of each controller in case 1
RMS ${x_e}$/m ${y_e}$/m ${z_e}$/m ${\psi _e}$/rad ${\theta _{e1}}$/rad ${\theta _{e2}}$/rad RMPCESO 0.001 1 0.002 2 0.000 2 0.008 1 0.004 8 0.009 1 NTSMC 0.001 2 0.010 9 0.001 3 0.060 6 0.033 9 0.015 9 PID 0.062 1 0.029 9 0.080 4 0.040 8 0.021 7 0.049 2 表 2 工况2下各控制器跟踪误差RMS指标
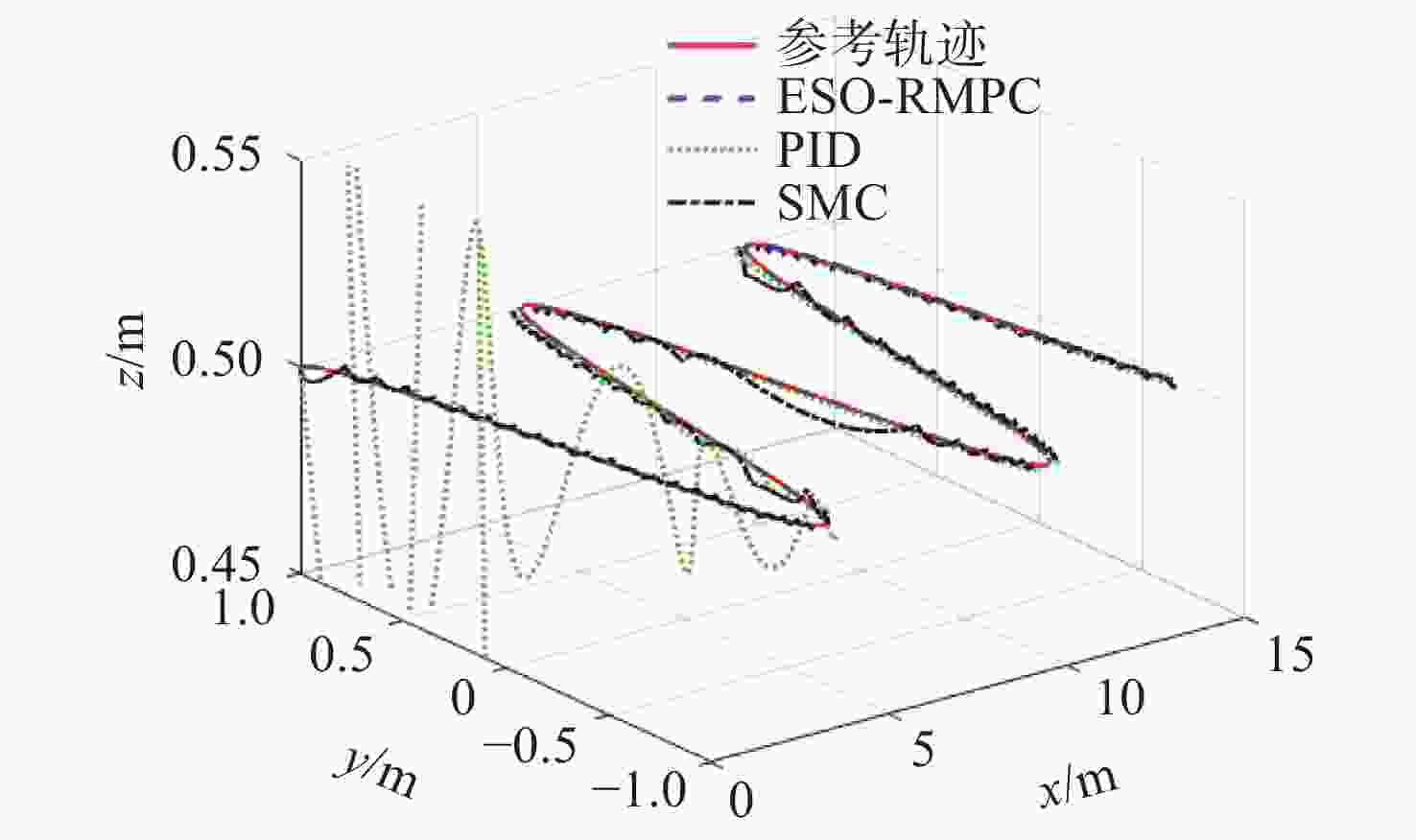
Table 2. The tracking error of each controller in case 2
RMS ${x_e}$/m ${y_e}$/m ${z_e}$/m ${\psi _e}$/rad ${\theta _{e1}}$/rad ${\theta _{e2}}$/rad RMPCESO 0.000 3 0.000 3 0.000 1 0.002 3 0.004 9 0.000 5 NTSMC 0.008 3 0.111 7 0.036 1 0.040 3 0.004 2 0.730 1 PID 0.030 2 0.145 2 0.044 8 0.011 4 0.013 3 0.073 2 -
[1] Paull L, Saeedi S, Seto M, et al. AUV navigation and localization: A review[J]. IEEE Journal of Oceanic Engineering, 2014, 39(1): 131-149. doi: 10.1109/JOE.2013.2278891 [2] Lapierre L, Jouvencel B. Robust nonlinear path-following control of an AUV[J]. IEEE Journal of Oceanic Engineering, 2008, 33(2): 89-102. doi: 10.1109/JOE.2008.923554 [3] Stutters L, Liu H, Tiltman C, et al. Navigation technologies for autonomous underwater vehicles[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C(Applications and Reviews), 2008, 38(4): 581-589. doi: 10.1109/TSMCC.2008.919147 [4] Ishitsuka M, Ishii K. Development and control of an underwater manipulator for AUV[C]//Symposium on Underwater Technology & Workshop on Scientific Use of Submarine Cables & Related Technologies. Tokyo, Japan: IEEE, 2007. [5] Cai M, Wang Y, Wang S, et al. Grasping marine products with hybrid-driven underwater vehicle-manipulator system[J]. IEEE Transactions on Automation Science and Engineering, 2020, 99: 1-12. [6] Olguin-Diaz E, Arechavaleta G, Jarquin G, et al. A passivity-based model-free force-motion control of underwater vehicle-manipulator systems[J]. IEEE Transactions on Robotics, 2013, 29(6): 1469-1484. doi: 10.1109/TRO.2013.2277535 [7] Jarzebowska E. Model reference tracking control for constrained robotic systems[C]// Proceedings of the Third International Workshop on Robot Motion and Control. Bukowy Dworek, Poland: IEEE, 2002. [8] Fossen T I. Guidance and control of ocean vehicles[J]. Automatica, 1996, 32(8): 1235. [9] Tarn T J, Shoults G A, Yang S P. Underwater robots[M]. US: Springer, 1996: 36-54. [10] Lin Z, Wang H D, Karkoub M, et al. Prescribed performance based sliding mode path-following control of UVMS with flexible joints using extended state observer based sliding mode disturbance observer[J]. Ocean engineering, 2021, 240: 109915. doi: 10.1016/j.oceaneng.2021.109915 [11] Antonelli G, Caccavale F, Chiaverini S, et al. Tracking control for underwater vehicle-manipulator systems with velocity estimation[J]. IEEE Journal of Oceanic Engineering, 2000, 25(3): 399-413. doi: 10.1109/48.855403 [12] Antonelli G, Caccavale F, Chiaverini S. Adaptive tracking control of underwater vehicle-manipulator systems based on the virtual decomposition approach[J]. IEEE Transactions on Robotics and Automation, 2004, 20(3): 594-602. doi: 10.1109/TRA.2004.825521 [13] Wang Y, Jiang S, Bai C, et al. Trajectory tracking control of underwater vehicle-manipulator system using discrete time delay estimation[J]. IEEE Access, 2017, 5: 7435-7443. doi: 10.1109/ACCESS.2017.2701350 [14] Akter P, Uddin M, Mekhilef S, et al. Model predictive control of bidirectional isolated DC-DC converter for energy conversion system[J]. International Journal of Electronics, 2015, 102(8): 1407-1427. doi: 10.1080/00207217.2015.1028479 [15] Yang W, Boyd S. Fast model predictive control using online optimization[J]. IEEE Transactions on Control Systems Technology, 2010, 18(2): 267-278. doi: 10.1109/TCST.2009.2017934 [16] Scokaert P O M, Mayne D Q. Min-max feedback model predictive control for constrained linear systems[J]. IEEE Transactions on Automatic Control, 1998, 43(8): 1136-1142. doi: 10.1109/9.704989 [17] Geyer T, Papafotiou G, Morari M. Model predictive direct torque control—Part I: Concept, algorithm, and analysis[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1894-1905. doi: 10.1109/TIE.2008.2007030 [18] Shen C, Shi Y, Buckham B. Integrated path planning and tracking control of an AUV: A unified receding horizon optimization approach[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(99): 1163-1173. [19] Li D, Yu Y, Zhai D H, et al. Robust model predictive tracking control for robot manipulators with disturbances[J]. IEEE Transactions on Industrial Electronics, 2021, 68(5): 4288-4297. doi: 10.1109/TIE.2020.2984986 [20] Dai Y, Yu S, Yan Y, et al. An EKF-based fast tube MPC scheme for moving target tracking of a redundant underwater vehicle-manipulator system[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(6): 2803-2814. doi: 10.1109/TMECH.2019.2943007 [21] Low K S, Zhuang H. Robust model predictive control and observer for direct drive applications[J]. IEEE Transactions on Power Electronics, 2000, 15(6): 1018-1028. doi: 10.1109/63.892816 [22] Mata S, Zubizarreta A, Pinto C. Robust tube-based model predictive control for lateral path tracking[J]. IEEE Transactions on Intelligent Vehicles, 2019, 4(4): 569-577. doi: 10.1109/TIV.2019.2938102 [23] Kayacan E, Ramon H, Saeys W. Robust trajectory tracking error model-based predictive control for unmanned ground vehicles[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(2): 806-814. doi: 10.1109/TMECH.2015.2492984 [24] Bechlioulis C P, Rovithakis G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J]. IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099. doi: 10.1109/TAC.2008.929402 [25] Bidram A, Davoudi A, Lewis F L, et al. Distributed cooperative secondary control of microgrids using feedback linearization[J]. IEEE Transactions on Power Systems, 2013, 28(3): 3462-3470. doi: 10.1109/TPWRS.2013.2247071 -




 下载:
下载: