Continuous Wave Signal Detection Based on Weight Vector under Colored Gaussian Noise
-
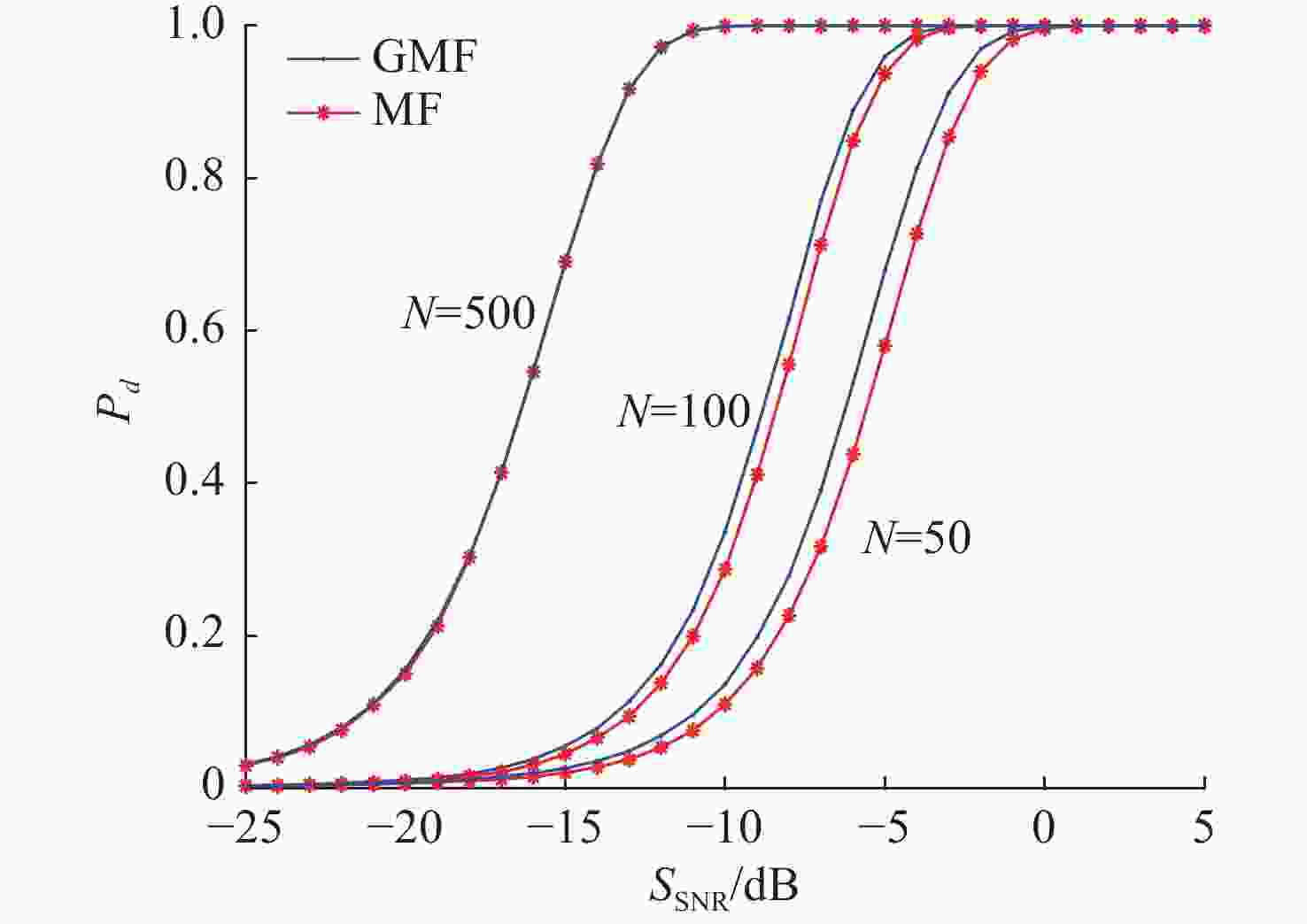
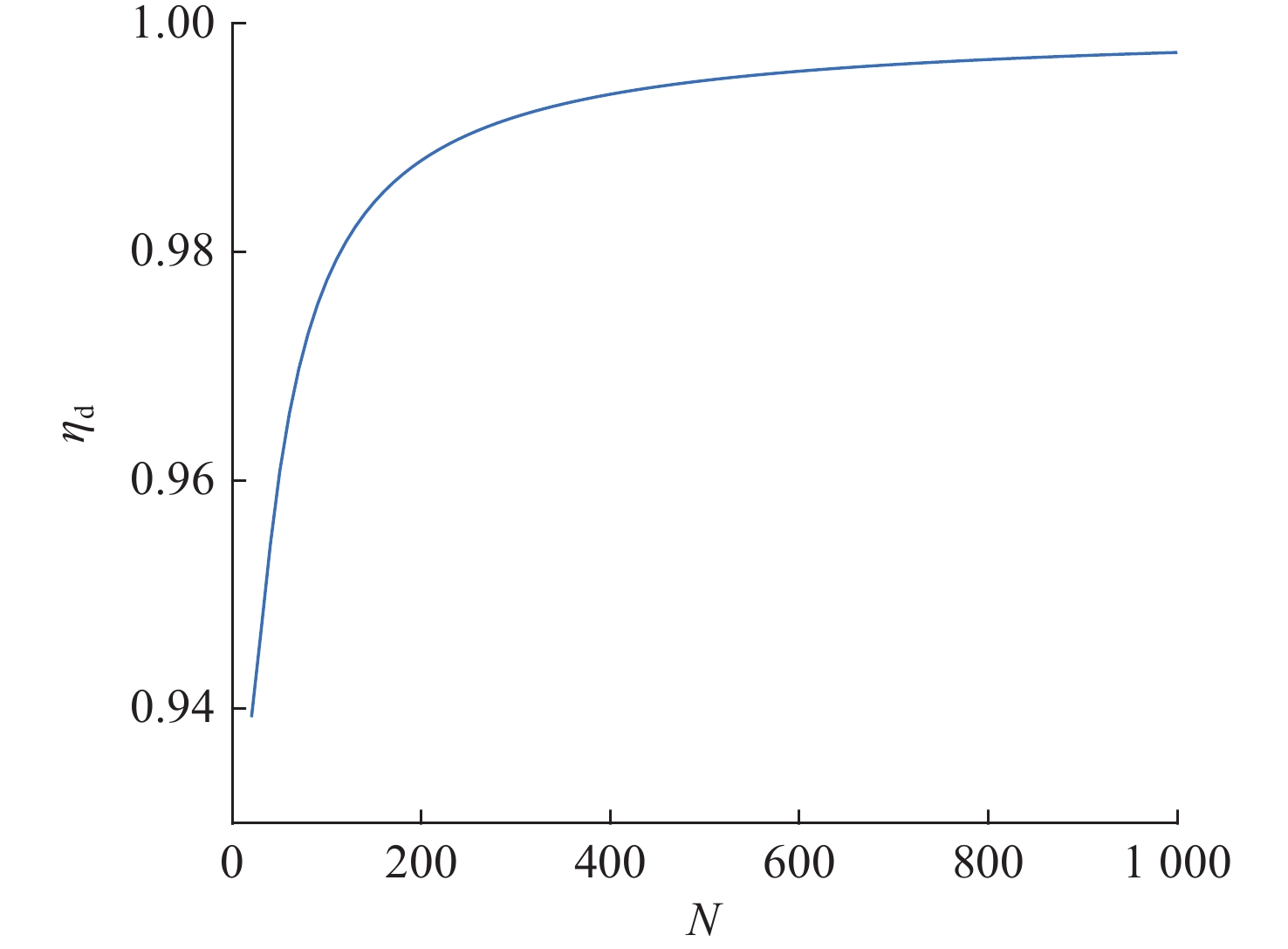
摘要: 针对高斯色噪声背景下信号检测需要进行预白化处理的问题, 提出了一种基于权向量的信号检测方法。首先基于权向量构造检验统计量, 分析其检测性能, 在此基础上推导了N-P准则下的最优权向量, 并证明了其与广义匹配滤波的等价性。通过构造合适的权向量, 证明在大数据记录下检测连续波信号时无须进行预白处理, 可以明显提高检测效率。仿真结果表明了该检测方法的有效性。Abstract: Signal detection under colored Gaussian noise needs pre-white processing. In view of this, a signal detection method based on a weight vector was proposed. Firstly, the test statistics were constructed based on the weight vector, and its detection performance was analyzed. On this basis, the optimal weight vector under the N-P criterion was derived, and its equivalence with the generalized matched filter was proved. By constructing a suitable weight vector, it was proved that there was no need for prewhitening when continuous wave signals were detected in big data records, which significantly improved the detection efficiency. The simulation results verify the effectiveness of the detection method.
-
Key words:
- colored Gaussian noise /
- weight vector /
- signal detection /
- continuous wave signal /
- prewhitening
-
0. 引言
连续波(continuous wave, CW)信号作为一种比较简单的发射信号波形, 在雷达、声呐以及声自导鱼雷中受到了广泛应用[1-3]。在高斯白噪声背景下, 检测CW信号的最佳检测器为匹配滤波器(matched filter, MF)[4]。然而在实际检测过程中, 背景通常是有色的。高斯色噪声背景下的最佳检测器则为广义匹配滤波器(generalized matched filter, GMF)。GMF的思路是通过一定的变换, 将色噪声背景下的信号检测问题转化为白噪声背景下的检测问题, 从而应用MF完成检测[5]。
GMF的核心在于对色噪声进行预白处理。常见的预白化方法主要包括Karhunen-Loève变换法、Cholesky分解法以及增强现实(augmented reality, AR)预白化法等[6-8]。但除AR预白化法外, 其他预白化法都要求色噪声的协方差矩阵是先验已知的, 这在实际过程中通常难以满足。AR预白化法虽然可以根据接收信号实时估计色噪声的协方差矩阵, 但也存在定阶困难和计算量大等问题[9]。
为此, 文中提出一种基于权向量的信号检测方法, 该方法在大数据记录下(采样点数足够多时)检测CW信号时, 无需进行预白处理, 并且检测性能和GMF相当。
1. 信号检测模型
考虑如下检测模型
$$ \begin{array}{l}{H}_{0}: {x}_{n}={w}_{n}n=0,1,\cdots ,N-1\\ {H}_{1}: {x}_{n}={s}_{n}+{w}_{n}n=0,1,\cdots ,N-1\end{array} $$ (1) 式中:
$ {x_n} $ 是接收信号;$ {s_n} $ 是待检测信号;$ {w_n} $ 是零均值的平稳高斯色噪声, 其协方差矩阵为$ {{\boldsymbol{C}}_w} $ , 是对称正定toeplitz矩阵。记
$ {\boldsymbol{S}} = {[{s_0},{s_1}, \cdots ,{s_{N-1}}]^{\rm{T}}} $ ,$ {\boldsymbol{X}} = {[{x_0},{x_1}, \cdots ,{x_{N-1}}]^{\rm{T}}} $ , 易知X是N维高斯随机矢量, 在假设$ {H_0} $ 和$ {H_1} $ 下其概率分布为$$ {\boldsymbol{X}}\sim\left\{ \begin{gathered} \mathbb{N}(0,\;\;{{\boldsymbol{C}}_w})\;\;\;\;\;\;\;{H_0} \\ \mathbb{N}({\boldsymbol{S}},\;\;{{\boldsymbol{C}}_w})\;\;\;\;\;\;\;{H_1} \\ \end{gathered} \right. $$ (2) 对于上述信号检测模型, 根据经典的统计信号检测理论可知, 其最佳检测器为GMF, 对应的检验统计量为[10]
$$ {G_{{\text{GMF}}}} = {{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{X}} $$ (3) 2. 基于权向量的信号检测
2.1 检验统计量构造
由式(3)可以看出,
$ {G_{{\text{GMF}}}} $ 是接收信号矢量X的线性组合, 是一个线性检测器。因此基于权向量构造一个线性检验统计量, 即$$ {{{G}}_{\boldsymbol{\beta}} } = {{\boldsymbol{\beta }}^{\rm{T}}}{\boldsymbol{X}} $$ (4) 式中,
$ {\boldsymbol{\beta}} = {[{\beta _0},{\beta _1}, \cdots ,{\beta _{N-1}}]^{\rm{T}}} $ 为权向量。2.2 检测性能分析
由于
${G_{\boldsymbol{\beta}} }$ 也是X的线性组合, 易知${G_{\boldsymbol{\beta}} }$ 是一维高斯随机变量, 其概率分布为$$ {G_{\boldsymbol{\beta }}}\sim \left\{ \begin{gathered} \mathbb{N}(0,\;\;{{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} )\;\;\;\;\;\;\;\;\;\;{H_0} \\ \mathbb{N}({{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}},\;\;{{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} )\;\;\;\;\;\;{H_1} \\ \end{gathered} \right. $$ (5) 由式(5)可知, 在不同假设下
${G_{\boldsymbol{\beta }}}$ 的均值不等而方差相等。可以证明, 以${G_{\boldsymbol{\beta}} }$ 作为检验统计量时, 其虚警概率$ {P_f} $ 与检测概率$ {P_d} $ 总满足[10]$$ {P_d} = Q\left( {{Q^{ - 1}}({P_f}) - \sqrt {{d^2}} } \right) $$ (6) 式中:
$Q(x) = \displaystyle \int_x^{ + \infty } {\dfrac{1}{{\sqrt {2{\text{π}} } }}} {{\rm{e}}^{{{ - {t^2}} / 2}}}{\rm{d}}t$ , 为标准正态概率右尾函数;$ {Q^{ - 1}}(x) $ 是$ Q(x) $ 的反函数;$ {d^2} $ 通常称为检测指数。由式(6)可以看出, 在给定虚警概率时, 信号的检测概率完全由检测指数
$ {d^2} $ 决定, 其计算公式为$$ {d^2} = \frac{{{{[E(G/{H_1}) - E(G/{H_0})]}^2}}}{{Var(G/{H_0})}} $$ (7) 式中,
$ E(G/{H_j}) $ 与$ Var(G/{H_j}) $ 分别是假设$ {H_j}(j = 0,1) $ 下检验统计量G的均值与方差。结合式(5)和式(7)可得
$G = {G_\beta }{\text{ = }}{{\boldsymbol{{\boldsymbol{\beta}}}} ^{\rm{T}}}{\boldsymbol{X}}$ 时的检测指数为$$ {d^2}({\boldsymbol{\beta}} ) = \frac{{{{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}}{{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}}}}{{{{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} }} $$ (8) 2.3 N-P准则下的最优权向量
在雷达、声呐以及声自导鱼雷中, 通常采用N-P准则作为最佳判决准则, 即给定虚警概率, 使得检测概率最大。由式(6)可知在虚警概率一定时, 检测概率是检测指数
$ {d^2} $ 的单调递增函数, 因此使得$ {d^2} $ 取最大值时的权向量就是N-P准则下的最优权向量。下面推导最优权向量的表达式。在式(8)两端同时对权向量
${\boldsymbol{ \beta}} $ 求导可得$$ \begin{align} \frac{{\partial \left[ {{d^2}({\boldsymbol{\beta}} )} \right]}}{{\partial {\boldsymbol{\beta}} }} =&\; \frac{{2S{{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}}{{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} - 2{{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}}{{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} }}{{{{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} {{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} }}= \\ &\;\frac{{2{{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}}}}{{{{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} }}\left( {{\boldsymbol{S}} - \frac{{{{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} }}{{{{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} }}} \right) \\ \end{align} $$ (9) 由于
$\dfrac{{{{\boldsymbol{\beta}} ^{\rm{T}}}{\boldsymbol{S}}}}{{{{\boldsymbol{\beta}} ^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} }}$ 是一个标量, 可记其为k。令式(9)等于零, 可得$2k({\boldsymbol{S}} - k{{\boldsymbol{C}}_w}{\boldsymbol{\beta}} ) = 0$ , 即$$ {\boldsymbol{\beta}} = \frac{1}{k}{\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}} $$ (10) 由于常系数对信号检测没有影响, 为方便起见, 可直接取最优权向量为
${{\boldsymbol{\beta }}_m} = {\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}}$ , 将其代入式(4)可得最优检验统计量为$$ {G_m} = {({\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}})^{\text{T}}}{\boldsymbol{X}} = {{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{X}} $$ (11) 对比式(3)和式(11)可以发现, 根据最优权向量构造的最优检验统计量
$ {G_m} $ 和$ {G_{{\text{GMF}}}} $ 的表达式完全一样, 这与GMF是高斯色噪声背景下最佳线性检测器的结论一致。将
${{\boldsymbol{\beta}} _m} = {\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}}$ 代入式(8)可得$$ {d^2}({{{{\boldsymbol{\beta}}}} _m}) = \frac{{{{{{\boldsymbol{\beta}}}} _m}^{\rm{T}}{\boldsymbol{S}}{{{{\boldsymbol{\beta}}}} _m}^{\rm{T}}{\boldsymbol{S}}}}{{{{{{\boldsymbol{\beta}}}} _m}^{\rm{T}}{{\boldsymbol{C}}_w}{{{{\boldsymbol{\beta}}}} _m}}} = {{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}} $$ (12) 显然, GMF的检测性能同样可由式(12)确定的检测指数决定。
3. CW信号检测
当待检测信号
$ {s_n} $ 为CW信号时, 可写为$$ {s_n} = A\sin (2{\text{π}} {f_c}n + \theta ){\kern 1pt} {\kern 1pt} $$ (13) 式中:
$ {f_c} $ 为归一化后的信号频率; A、$ \theta $ 分别为CW信号的幅值与相位。对于单次检测而言, 幅值A与相位$ \theta $ 通常未知, 但其值是确定的, 因此可视为确知信号检测。3.1 权向量选择
如果是在高斯白噪声背景下检测CW信号, 其最佳检测器为MF, 检验统计量为
$$ {G_{{\text{MF}}}} = {{\boldsymbol{S}}^{\text{T}}}{\boldsymbol{X}} $$ (14) 对比式(14)和式(3)可以发现, GMF相比于MF多出一个因子
$ {\boldsymbol{C}}_w^{{ - 1}} $ 。由于$ {{\boldsymbol{C}}_w} $ 是色噪声的协方差矩阵, 所以$ {\boldsymbol{C}}_w^{{ - 1}} $ 的存在相当于对色噪声先进行了预白处理, 然后再进行MF检测。这也是GMF被称为广义匹配滤波的原因。但是, 对于色噪声背景下的CW信号检测, 如果直接应用GMF, 综合式(11)和式(12)可知, 无论是检验统计量计算还是检测性能分析, 都不可避免地涉及到
$ {\boldsymbol{C}}_w^{{ - 1}} $ 。然而,$ {{\boldsymbol{C}}_w} $ 一般不是先验已知的, 通常需要进行实时估计得到, 这将大大增加检测的计算量。为此考虑选择合适的权向量, 以避免预白处理, 也就是避免计算$ {\boldsymbol{C}}_w^{{ - 1}} $ 。显然, 一个最简单的方法是继续用MF在色噪声背景下检测CW信号, 这意味着直接取权向量为
$$ {\boldsymbol{\beta}} = {\boldsymbol{S}} $$ (15) 式(15)表达式虽然简单, 但色噪声下的检测性能并不是最优的, 需要进一步分析。
3.2 色噪声背景下MF性能分析
由于MF等价于权向量取为
$ {\boldsymbol{\beta}} = {\boldsymbol{S}} $ , 将其代入式(8)可得MF的检测指数为$$ {d^2}({\boldsymbol{S}}) = \frac{{{{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{S}}{{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{S}}}}{{{{\boldsymbol{S}}^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{S}}}} $$ (16) 定义MF和GMF的检测指数之比为
$ {\eta _d} $ , 可知其表达式为$$ {\eta _d} = \frac{{{d^2}({\boldsymbol{S}})}}{{{d^2}({\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}})}} = \frac{{{{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{S}}{{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{S}}}}{{{{\boldsymbol{S}}^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{S}}{{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}}}} $$ (17) 显然
$ {\eta _d} $ ＜1, 但如果$ {\eta _d} $ 越接近于1, 表明MF的检测性能越接近于GMF。下面证明, 当接收信号足够长, 即在大数据记录下
$ {\eta _d} $ 是等于1的。首先, 对于CW信号有
$$ {{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{S}} = \sum\limits_{n = 0}^{N - 1} {s_n^2} = \frac{{{A^2}N}}{2} $$ (18) 其次, 根据文献[10]可知, 在大数据记录下有
$$ \left\{ \begin{gathered} {{\boldsymbol{S}}^{\rm{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{S}} = \sum\limits_{i = 0}^{N - 1} {P({f_i})I({f_i})} \\ {{\boldsymbol{S}}^{\rm{T}}}{\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}} = \sum\limits_{i = 0}^{N - 1} {\frac{{I({f_i})}}{{P({f_i})}}} \\ \end{gathered} \right. $$ (19) 式中:
$ P(f) $ 是将色噪声频率归一化后的功率谱密度;$I(f) = \dfrac{1}{N}{\left| {\displaystyle \sum\limits_{n = 0}^{N - 1} {{s_n}{{\rm{e}}^{ - j2{\text{π}} fn}}} } \right|^2}$ 是信号$ {s_n} $ 的周期谱图;${f_i} = i/N(i = 0,1, \cdots ,N - 1)$ 是归一化后的信号频率。对于CW信号而言, 其周期谱图只在
$ {f_i} = {f_c} $ 和$ {f_i} = 1 - {f_c} $ (实际上对应的频率是$ - {f_c} $ )处有非零值, 而在其他频率处的周期谱图值均为零, 并且有$ I({f_c}) = I(1 - {f_c}) $ 。同时由于$ P(f) $ 是偶函数, 故有$ P({f_c}) = P(1 - {f_c}) = P( - {f_c}) $ 。将二者代入式(19)可得$$ \left\{ \begin{gathered} {{\boldsymbol{S}}^{\text{T}}}{{\boldsymbol{C}}_w}{\boldsymbol{S}} = 2P({f_c})I({f_c}) \\ {{\boldsymbol{S}}^{\text{T}}}{\boldsymbol{C}}_w^{{ - 1}}{\boldsymbol{S}} = 2×\frac{{I({f_c})}}{{P({f_c})}} \\ \end{gathered} \right. $$ (20) 根据Parseval定理, 确知信号的时域能量等于其频域能量, 故有
$$ \sum\limits_{i = 0}^{N - 1} {I({f_i})} = 2I({f_c}) = \sum\limits_{n = 0}^{N - 1} {s_n^2 = } \frac{{{A^2}N}}{2} $$ (21) 将式(18)、(20)和(21)代入式(17)可得
$$ {\eta _d} = \frac{{{{({A^2}N/2)}^2}}}{{2P({f_c})I({f_c}) \cdot {{2I({f_c})}}/{{P({f_c})}}}} = \frac{{{{({A^2}N/2)}^2}}}{{{{({A^2}N/2)}^2}}} = 1 $$ (22) 表明在大数据记录下, MF和GMF的检测指数相等, 即MF和GMF的检测性能是一样的。
4. 仿真分析
假设高斯色噪声背景
$ {w_n} $ 可以用M阶AR模型来拟合, 即$$ {w_n} = - \sum\limits_{k = 1}^M {{a_k}{w_{n - k}} + {u_n}} $$ (23) 式中:
$ {a_k} $ 为AR模型系数;$ {u_n} $ 是均值为0、方差为1的高斯白噪声。取采样频率为1 600 Hz, CW信号归一化频率为0.15。采用4阶AR模型来模拟高斯色噪声, AR模型参数取[−0.38, 0.36, 0.16, 0.17]。采样点数为N, 仿真结果如下。
图1给出了
$ {\eta _d} $ 与采样点数N的关系。可以明显看出, 当采样点数N较小时,$ {\eta _d} $ 取值与1相差较大; 随着N的增加,$ {\eta _d} $ 取值也迅速增加; 当$ N > 300 $ 时,$ {\eta _d} $ 取值较为平稳, 接近于1。
图 1 N-$ {{\boldsymbol{\eta}} _{\boldsymbol{d}}} $ 曲线Figure 1. Curve of N-$ {{\boldsymbol{\eta}} _{\boldsymbol{d}}} $ 约束虚警概率为
$ {P_f} = {10^{ - 3}} $ , 取采样点数N分别为50、100、500, 统一进行20 000次蒙特卡洛实验, MF与GMF的检测性能对比见图2。图中横坐标为信噪比, 记为SSNR, 且$ {S_{{\text{SNR}}}} = 10\log ({A^2}/\sigma _w^2) $ 。从图2首先可以看出, 当采样点数比较少时(
$ N = 50 $ ), GMF的检测性能优于MF, 前者比后者高出1 dB左右, 这与GMF是高斯色噪声背景下的最优检测器一致。同时还可以看出, 随着采样点数的增加, MF的检测性能逐渐逼近GMF, 当采样点数较大时($ N = 500 $ ), MF与GMF的检测性能曲线几近完全重合, 这与文中的结论一致。5. 结束语
针对高斯色噪声背景下的信号检测问题, 提出了一种基于权向量的检验统计量构造方法, 推导了N-P准则下的最优权向量, 证明根据最优权向量确定的检测器与GMF一致。将权向量应用到CW信号检测中, 证明了大数据记录下MF和GMF的检测性能是等价的, 仿真结果证明所提方法在检测CW信号时可以避免预白化处理, 明显提高检测效率。但是, 检测调频信号时, 仍然要进行预白化处理, 下一步可针对色噪声背景下调频信号的检测, 研究相应权向量的选择。
-
图 1 N-
$ {{\boldsymbol{\eta}} _{\boldsymbol{d}}} $ 曲线Figure 1. Curve of N-
$ {{\boldsymbol{\eta}} _{\boldsymbol{d}}} $ -
[1] 雷江涛, 董萌, 张国锋. 浅水环境鱼雷声自导波形设计与分析[J]. 鱼雷技术, 2016, 24(5): 346-350.Lei Jiangtao, Dong Meng, Zhang Guofeng. Waveform design and analysis of torpedo acoustic homing in shallow water[J]. Torpedo Technology, 2016, 24(5): 346-350. [2] 王晓江, 陈旭敏, 裴欣栋, 等. 雷达脉冲信号的非线性四阶检测接收机[J]. 现代雷达, 2017, 39(3): 69-74. doi: 10.16592/j.cnki.1004-7859.2017.03.016 [3] 夏文杰, 黎鑫, 曹伟浩, 等. 基于分数阶功率谱熵的未知水声脉冲信号检测方法[J]. 声学技术, 2021, 40(3): 415-421. doi: 10.16300/j.cnki.1000-3630.2021.03.019 [4] 杨波, 朱敏, 武岩波, 等. 一种在色噪声环境下的信号检测方法[J]. 应用声学, 2015, 34(1): 85-89. doi: 10.11684/j.issn.1000-310X.2015.01.013 [5] 李海宁, 苏小应, 俞卞章, 等. 一种改进的有色噪声背景下信号的检测算法[J]. 计算机仿真, 2009, 26(1): 355-357. doi: 10.3969/j.issn.1006-9348.2009.01.094 [6] Ruiz-Molina J C, Navarro-Moreno J, Oya A. Signal detection using approximate Karhunen-Loève expansions[J]. IEEE Transactions on Information Theory, 2001, 47(4): 1672-1680. [7] 齐志强. 基于Cholesky分解的自适应抗干扰算法[J]. 火力与指挥控制, 2019, 44(4): 150-153. doi: 10.3969/j.issn.1002-0640.2019.04.030 [8] 舒象兰, 孙荣光, 马鑫. 强混响背景下 LFM 信号回波检测[J]. 电讯技术, 2016, 56(1): 82-87. [9] 王志刚, 丁义明. 信噪比在AR模型定阶方法选择中的研究[J]. 数学物理学报: A辑, 2020, 40(3): 811-823. [10] 赵树杰. 信号检测与估计理论[M]. 北京: 电子工业出版社, 2013. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 189
- HTML全文浏览量: 31
- PDF下载量: 17
- 被引次数: 0
