A Calibration Method of Underwater Transponder Position Based on Maximum Correntropy
-
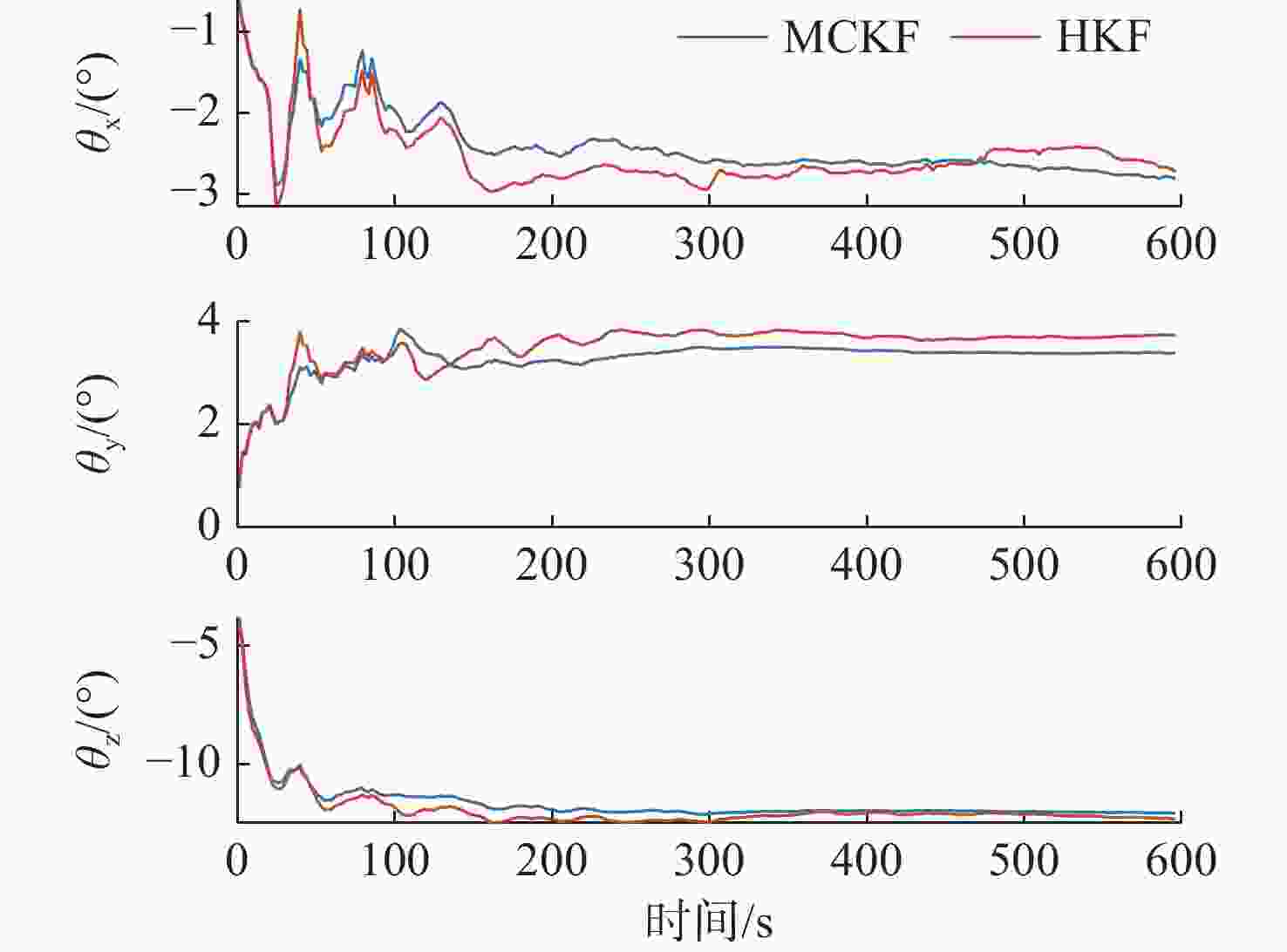
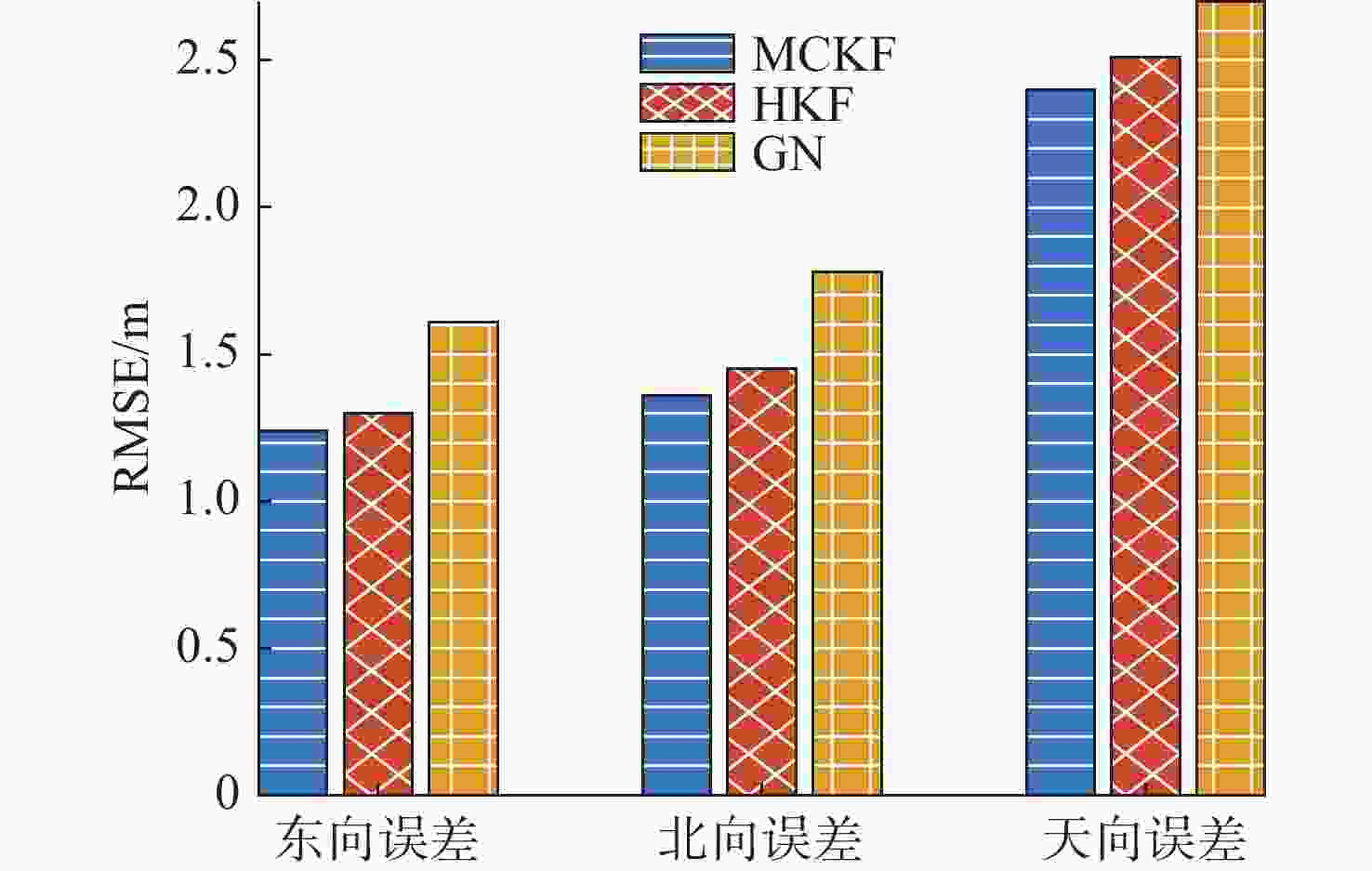
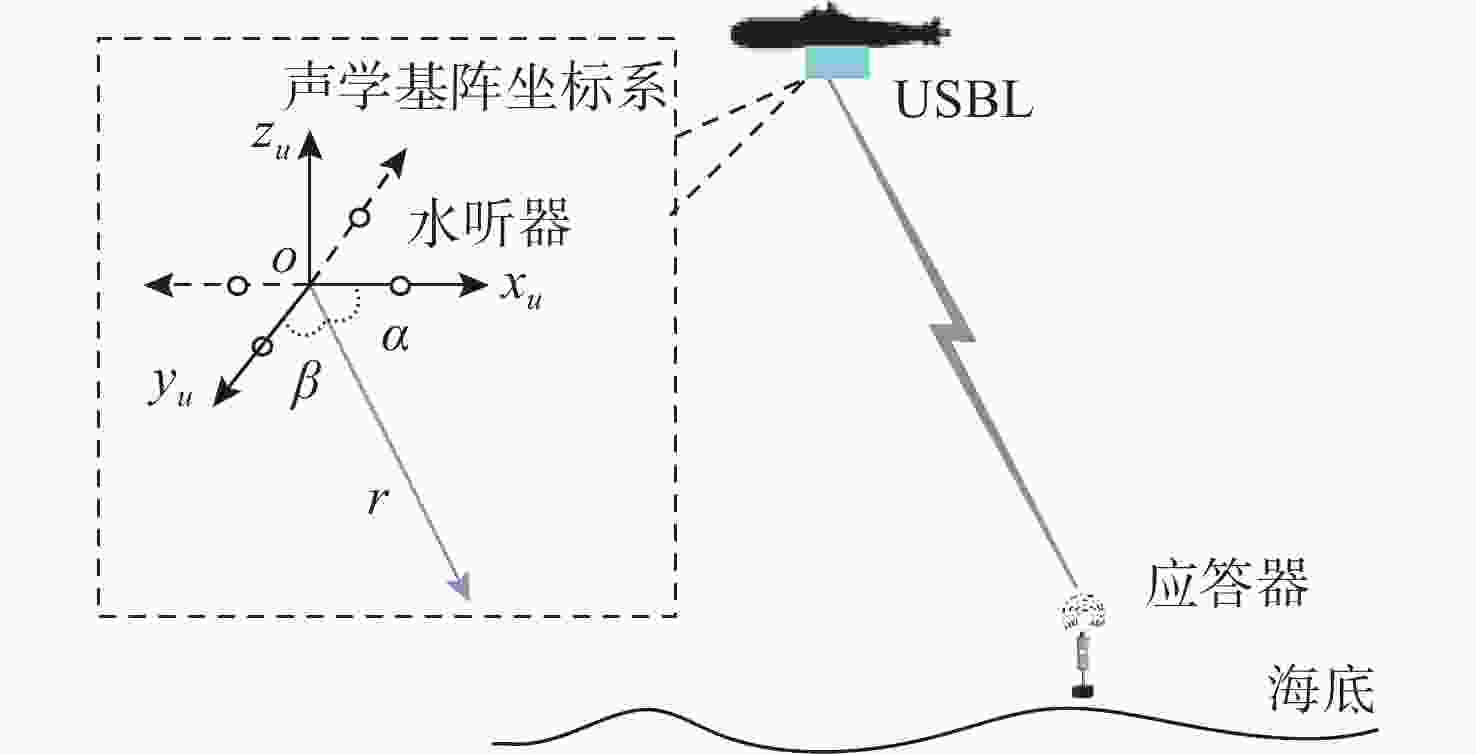
摘要: 超短基线(USBL)定位系统广泛应用于水下航行器的组合导航定位。已知的精确应答器位置是应用USBL进行导航定位的前提。传统应答器位置标定方法以斜距为观测量, 标定精度不高、鲁棒性差。文中以斜距和方位角为观测量, 推导了基于卡尔曼滤波的线性化量测方程。同时，考虑到水下复杂环境导致的噪声非高斯分布特性, 提出一种采用最大相关熵滤波抑制野值的水下声学应答器位置标定方法。在长江典型环境下对应答器位置进行标定试验，试验结果表明, 所提方法相比于传统方法具有更高的标定精度, 在野值干扰下具有更好的鲁棒性, 经标定后, 在东北天3个方向上USBL的定位精度分别提高了48.3%, 48.2%和40.4%, 可实现水下航行器高精度导航定位功能。Abstract: The ultra-short baseline(USBL) positioning system is widely used in the integrated navigation and positioning of underwater vehicles. Knowing the precise position of the transponder is a prerequisite for the application of the USBL system for navigation and positioning. The traditional calibration method of transponder position takes the slant distance as the observational variable. The calibration accuracy is not high, and the robustness is poor. The linearized measurement equation based on the Kalman filter was derived by taking slant distance and bearing angles as observational variables in this paper. In view of the non-Gaussian distribution of noise caused by complex underwater environments, a maximum correntropy filtering method was used to calibrate the position of an underwater acoustic transponder by suppressing outliers. Calibration experiments on the transponder position were carried out under the typical environment of the Yangtze River. Experimental results show that the proposed calibration method has higher calibration accuracy than the traditional method. It has better robustness under outlier interference. After calibration, the positioning accuracy of the USBL system has been improved by 48.3%, 48.2%, and 40.4% in the east-north-up coordinates. It can provide high-precision navigation and positioning functions for underwater vehicles.
-
图 2 基于MCKF的水下应答器位置标定方法
Figure 2. Calibration method of underwater transponder position based on MCKF
表 1 传感器参数
Table 1. Parameters of sensors
参数 值 IMU 陀螺仪 常值偏置 $< 0.01/\text{h}$ 随机游走 $< 0.005 /\text{h}$ 加速度计 常值偏置 $ < 100\;\mathrm{ug} $ 随机游走 $ < 50\;\mathrm{ug} $ USBL 定位误差 0.1 m+1% r 输出频率 1/2 Hz PHINS/GPS 定位误差 0.02~0.05 m 
下载: 导出CSV
-
[1] Tong J, Xu X, Zhang T, et al. A misalignment angle error calibration method of underwater acoustic array in strapdown inertial navigation system/ultrashort baseline integrated navigation system based on single transponder mode[J]. Review of Scientific Instruments, 2019, 90(8): 085001. doi: 10.1063/1.5100250 [2] Jin B, Xu X, Zhu Y, et al. Single-source aided semi-autonomous passive location for correcting the position of an underwater vehicle[J]. IEEE Sensors Journal, 2019, 19(9): 3267-3275. doi: 10.1109/JSEN.2019.2892840 [3] Zhang T, Chen L, Li Y. AUV underwater positioning algorithm based on interactive assistance of SINS and LBL[J]. Sensors, 2016, 16(42): 1-22. [4] 王健, 鲁金瑞, 郑栋, 等. 水下复杂环境下基于SINS/USBL/DVL多源信息融合的组合导航算法[J]. 导航定位与授时, 2022, 9(1): 76-84.Wang Jian, Lu jinrui, Zheng Dong, et al. Integrated navigation algorithm based on SINS/USBL/DVL multi-source information fusion in underwater complex environment[J]. Navigation Positioning and Timing, 2022, 9(1): 76-84. [5] 金博楠, 徐晓苏, 张涛, 等. 超短基线定位技术及在海洋工程中的应用[J]. 导航定位与授时, 2018, 5(4): 8-20. doi: 10.19306/j.cnki.2095-8110.2018.04.002Jin Bonan, Xu Xiaosu, Zhang Tao, et al. USBL technology and its applications in ocean engineering[J]. Navigation Positioning and Timing, 2018, 5(4): 8-20. doi: 10.19306/j.cnki.2095-8110.2018.04.002 [6] Han Y, Zheng C, Sun D. A high precision calibration method for long baseline acoustic positioning systems[J]. Chinese Journal of Acoustics, 2017, 36(4): 489-500. [7] 韩云峰, 郑翠娥, 孙大军. 长基线声学定位系统跟踪解算优化方法[J]. 声学学报, 2017, 42(1): 14-20.Han Yunfeng, Zheng Cuie, Sun Dajun. An optimized estimation method in long baseline acoustic positioning systems[J]. Chinese Journal of Acoustics, 2017, 42(1): 14-20. [8] 吴媛媛, 张森, 郭锦标. 基于高斯-牛顿法的水下导航系统校准算法研究[J]. 舰船电子工程, 2018, 38(11): 48-52. doi: 10.3969/j.issn.1672-9730.2018.11.013Wu Yuanyuan, Zhang Sen, Guo Jinbiao. Calibration algorithm of underwater navigation system based on Gauss-Newton algorithm[J]. Ship Electronic Engineering, 2018, 38(11): 48-52. doi: 10.3969/j.issn.1672-9730.2018.11.013 [9] 金博楠, 徐晓苏, 张涛, 等. 基于递推最小二乘的水下声学应答器在线标定方法[J]. 中国惯性技术学报, 2019, 27(6): 746-752.Jin Bonan, Xu Xiaosu, Zhang Tao, et al. Online position calibration for underwater acoustic transponder using recursive least squares[J]. Journal of Chinese Inertial Technology, 2019, 27(6): 746-752. [10] 罗才智, 杨鲲, 辛明真, 等. 抗差卡尔曼滤波及其在超短基线水下定位中的应用[J]. 海洋技术学报, 2020, 39(5): 46-52.Luo Caizhi, Yang Kun, Xin Mingzhen, et al. Anti-aberration Kalman filtering and its application in ultra-short baseline underwater positioning[J]. Journal of Ocean Technology, 2020, 39(5): 46-52. [11] Zhang L, Zhang T, Shin H S. A robust calibration method for the underwater transponder position based on Gauss-Newton iteration algorithm[C]//International Conference on Control, Mechatronics and Automation. Delftn, Netherlands: ICCMA, 2019: 448-453. [12] Zhang T, Zhang L, Shin H S, et al. A novel and robust calibration method for the underwater transponder position[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-12. [13] Bo X, Zhang J, Razzaqi A A. A novel robust filter for outliers and time-varying delay on an SINS/USBL integrated navigation model[J]. Measurement science & technology, 2021, 32(1): 1-14. [14] Hou B, He Z, Li D, et al. Maximum correntropy unscented kalman filter for ballistic missile navigation system based on SINS/CNS Deeply Integrated Mode[J]. Sensors, 2018, 18(6): 1724. doi: 10.3390/s18061724 [15] Bo X, Wang X, Zhang J, et al. Maximum correntropy delay kalman filter for SINS/USBL integrated navigation[J]. ISA Transactions, 2021, 117: 274-287. doi: 10.1016/j.isatra.2021.01.055 [16] 罗凯鑫, 吴美平, 范颖. 基于最大熵方法的鲁棒自适应滤波及其应用[J]. 系统工程与电子技术, 2020, 42(3): 667-673.Luo Kaixin, Wu Meiping, Fan Ying. Robust adaptive filtering based on maximum entropy method and its application[J]. System Engineering and Electronics, 2020, 42(3): 667-673. -
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 196
- HTML全文浏览量: 43
- PDF下载量: 53
- 被引次数: 0
