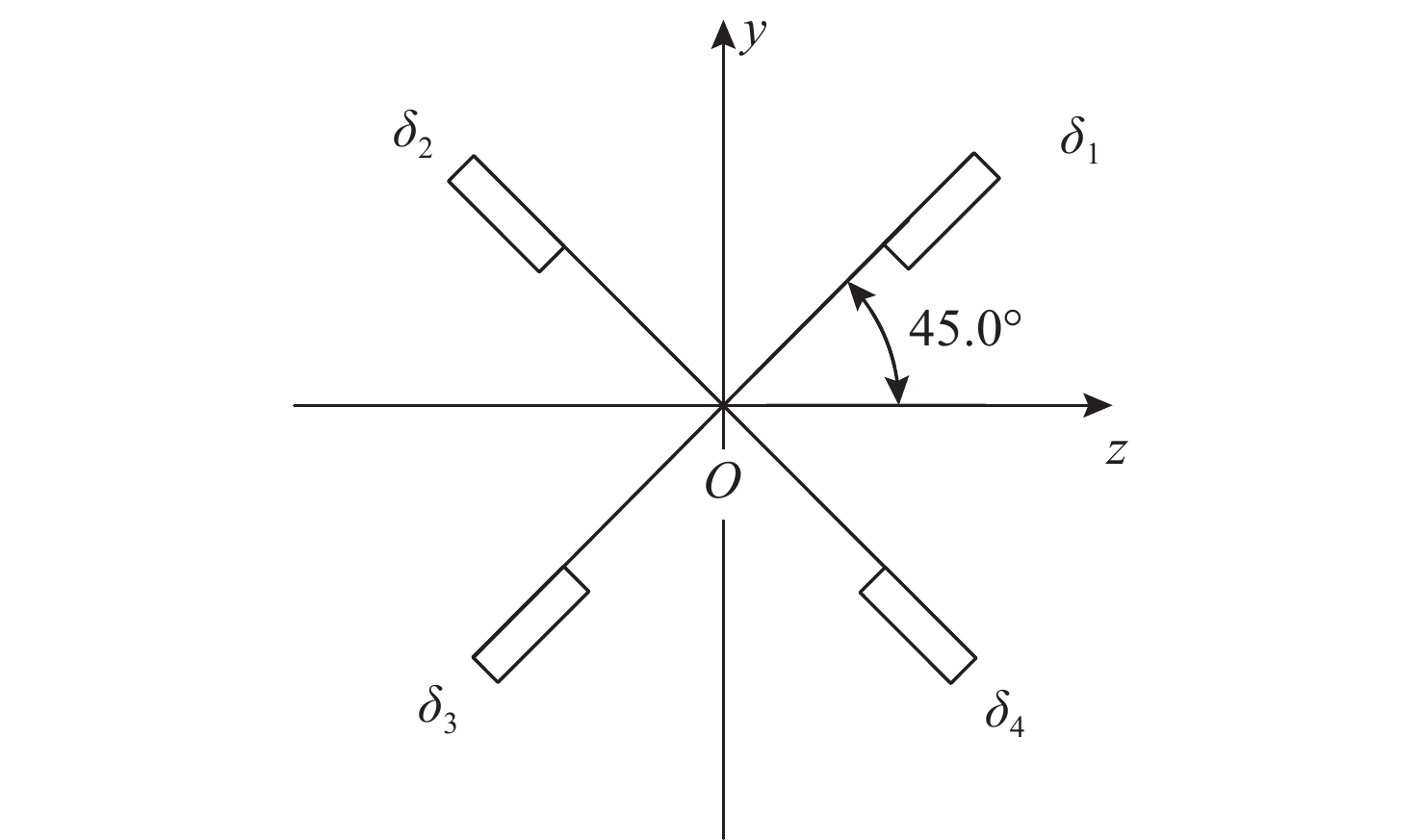
Influence of Design Parameters of High-Speed Undersea Vehicles with X-Shaped All-Movable Rudder and Cross-Shaped Fin on Maneuverability
-
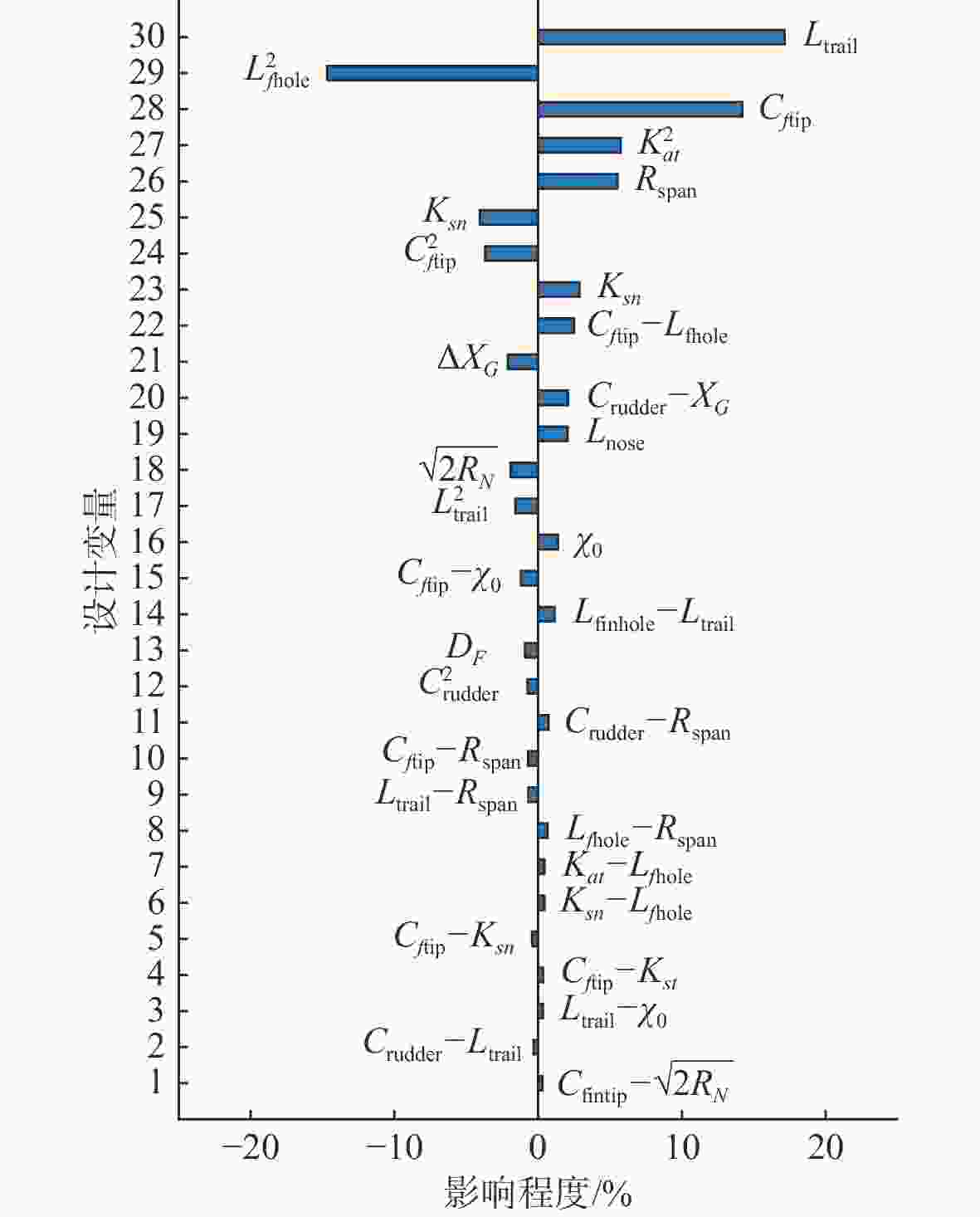
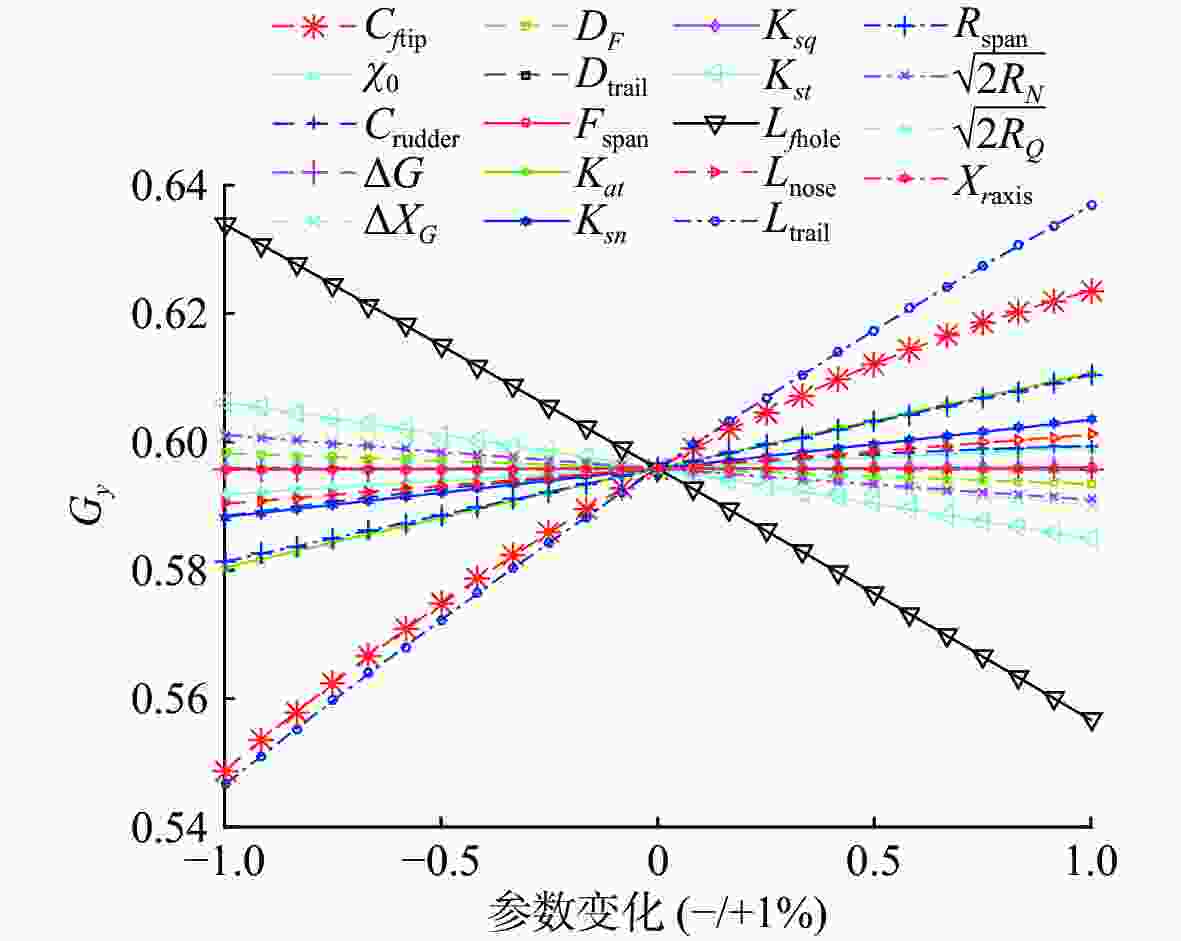
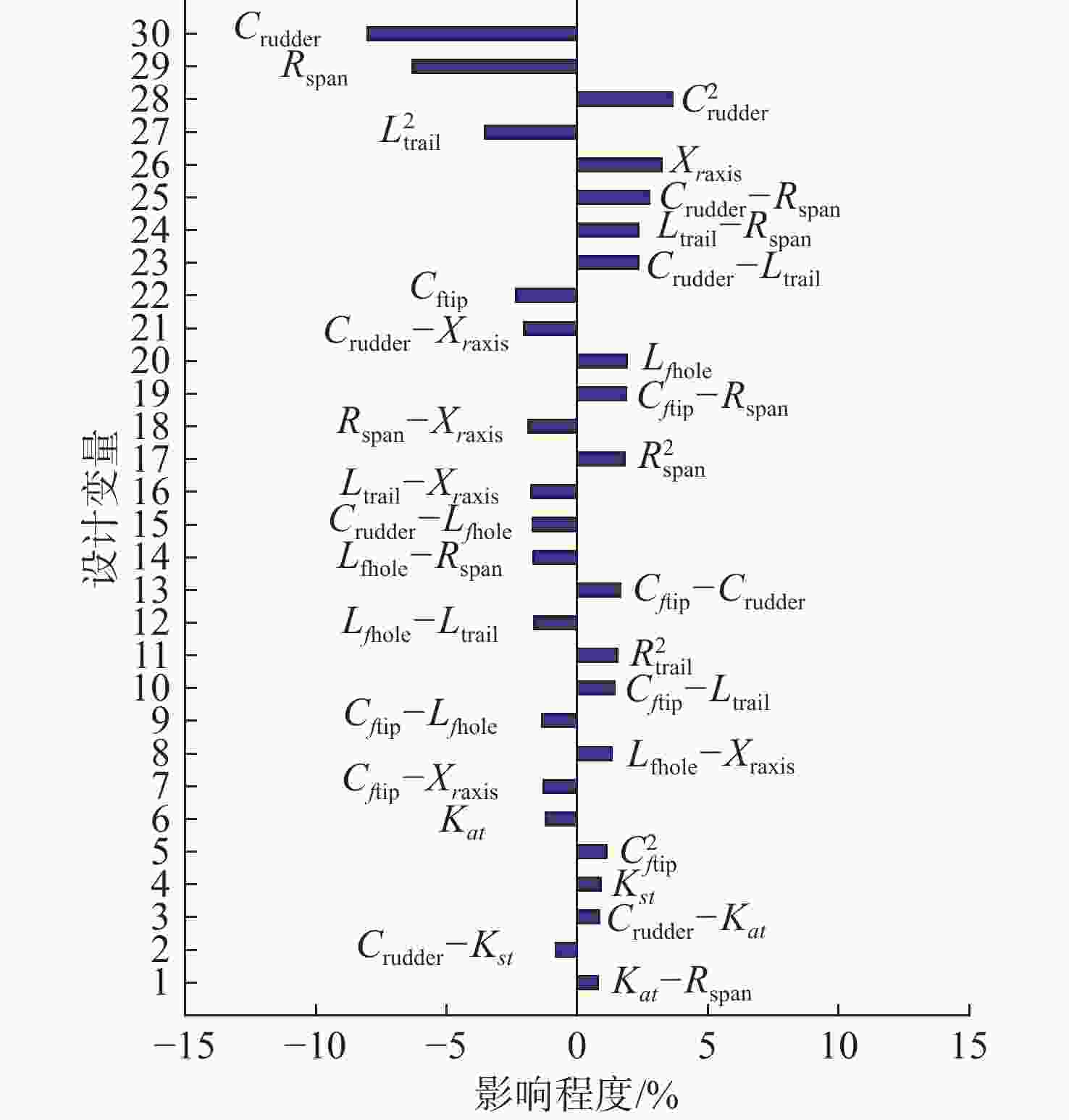
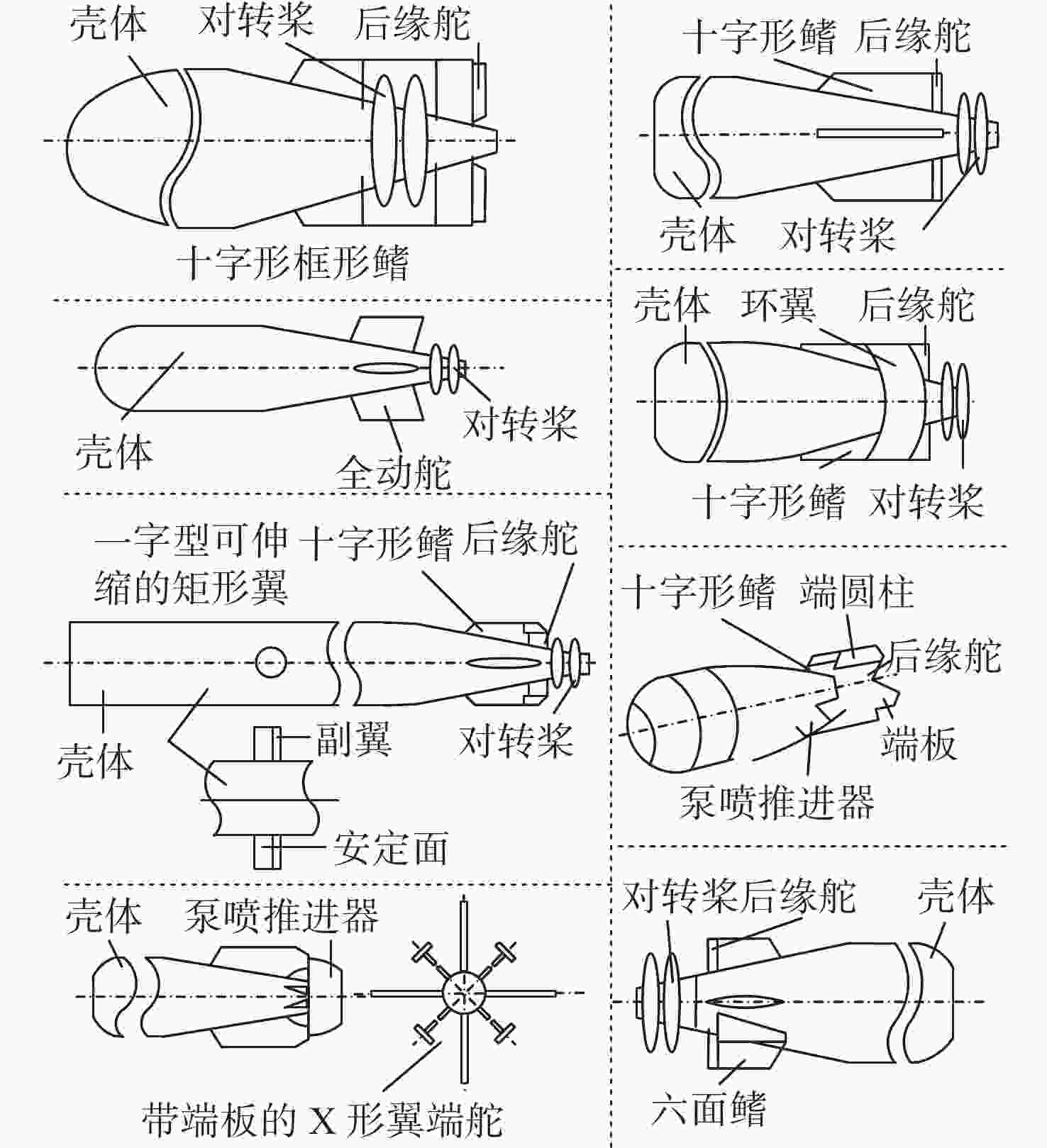
摘要: 针对X形全动舵十字形鳍布局的高速水下航行器外形结构, 采用部件叠加原理建立了航行器流体动力系数与各部分尺寸之间的函数模型, 建立了航行器流体动力、操纵稳定性和机动性与流体动力系数的关系。在给定各部件尺寸范围的前提下, 通过优化超立方拉丁抽样得到设计变量的样本区间, 采用试验设计思想分析了设计参数对航行器机动性能的影响程度, 以及操纵性能对设计参数变化的灵敏度。结果表明, 当设计参数在约束范围变化时, X形全动舵十字形鳍布局的高速水下航行器纵平面稳定度Gy和侧平面的动稳定度Gz均在0.4以上, 具有良好的机动能力; 航行器的负浮力大小与重心和浮心相对位置对航行器的Gy、Gz影响比较明显且呈现负效应; 全动舵的舵截面弦长和展长对航行器机动性能影响最大, 且全动舵宜设计为大展弦比舵并尽量安装在靠近尾部的位置。Abstract:
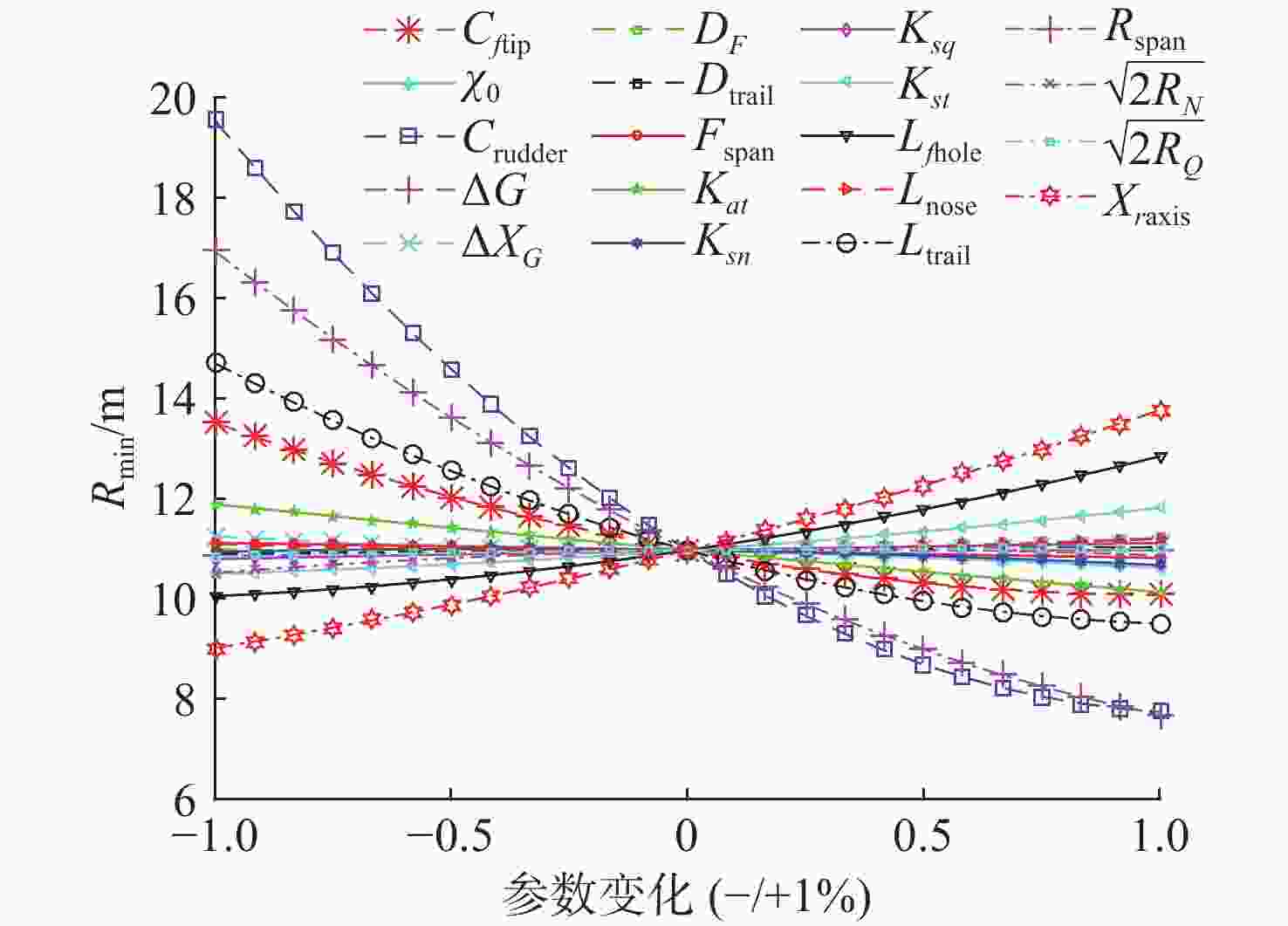
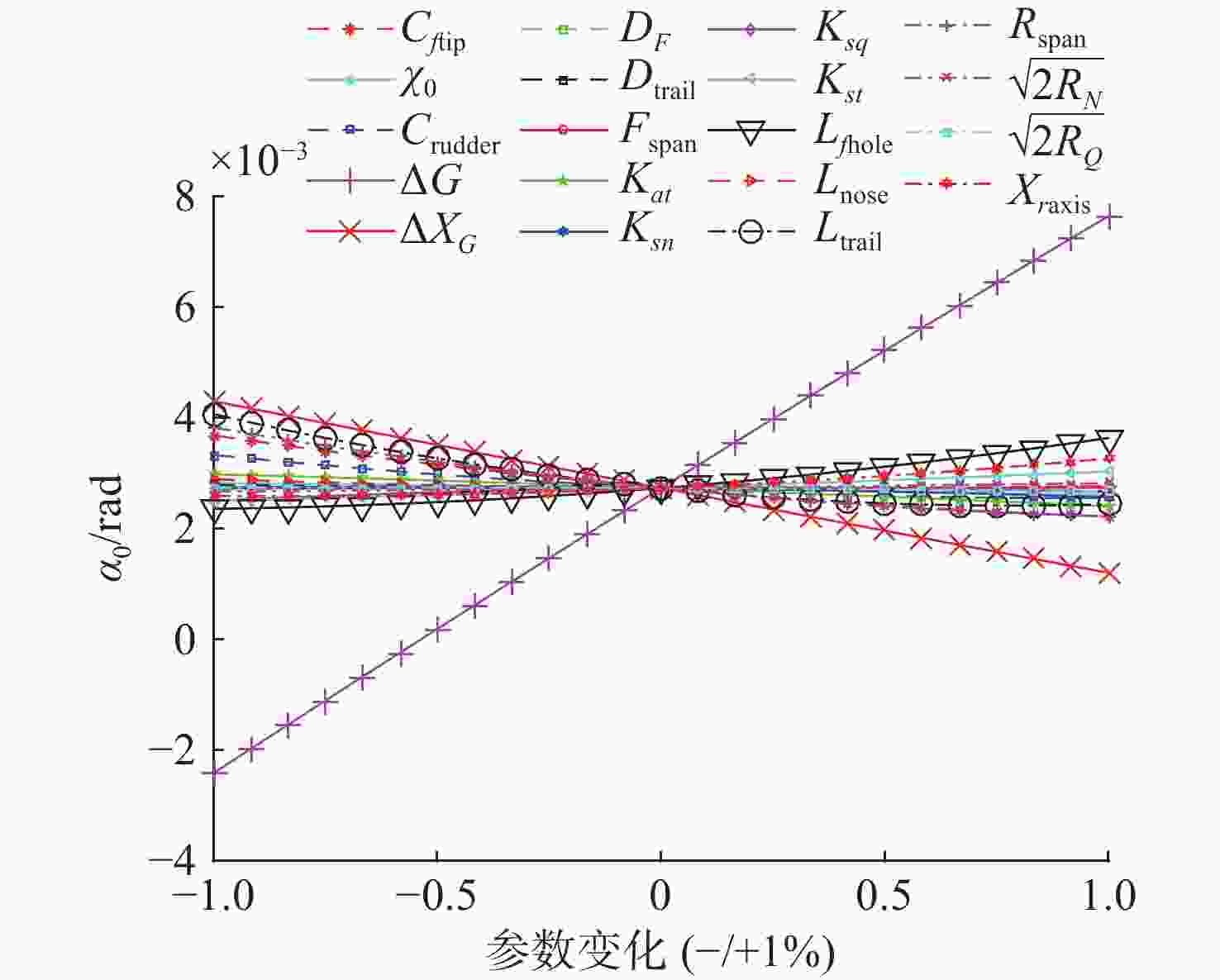
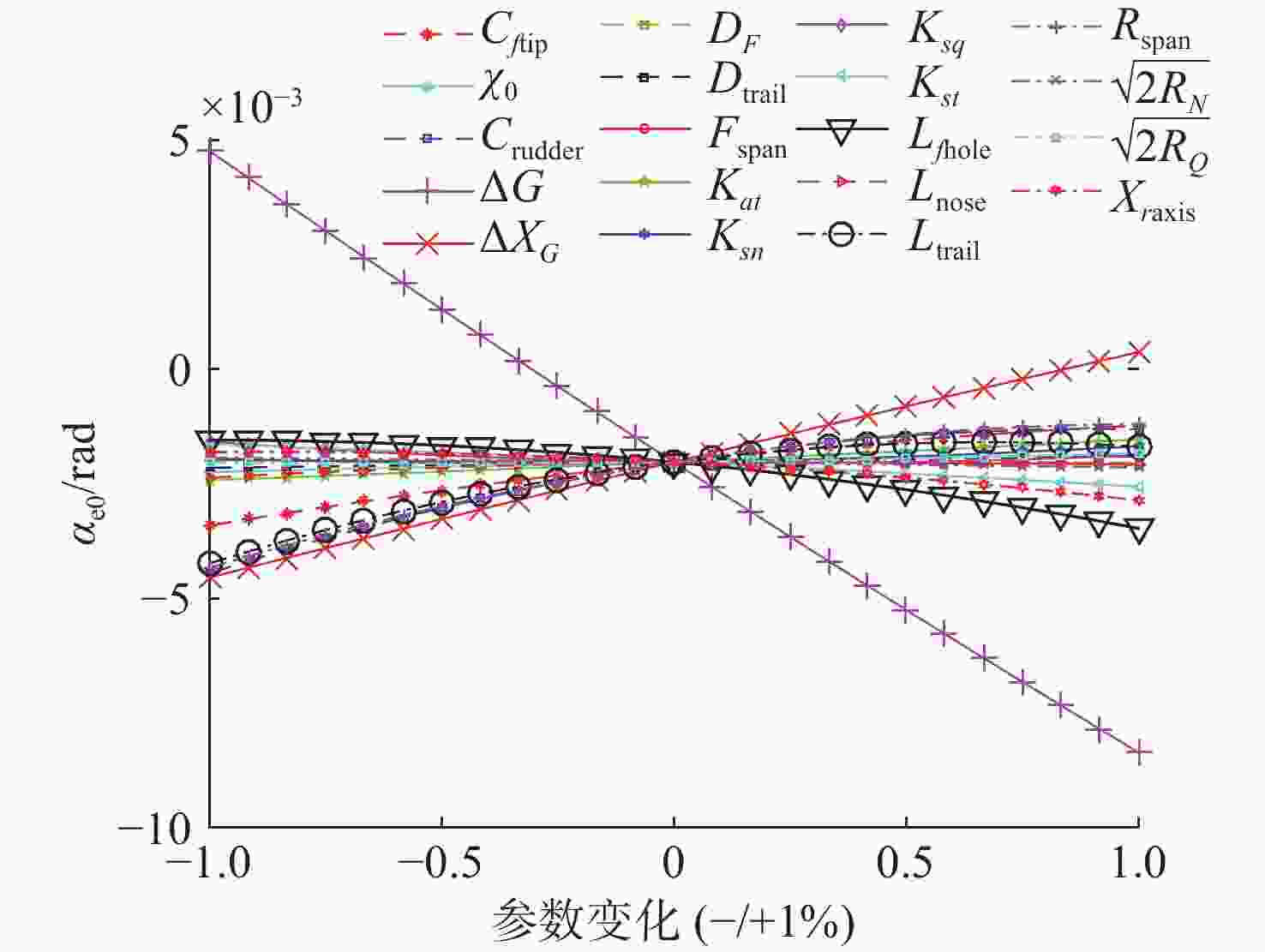
Parameterized shape of the undersea vehicle with X-shaped full-rudder and cross-shaped fin layout was established. The function of the fluid dynamic coefficient of the undersea vehicle with the size of each part was established by the principle of component superposition. The relationship between the fluid dynamics, steering stability, maneuverability of the vehicle and the hydrodynamic coefficient was established. Under the premise of the size range of each component, the sample interval of the design variables was obtained by optimizing the hypercube Latin sampling. The experimental design idea was used to analyze the influence degree of the design parameters on the maneuverability of the vehicle, the sensitivity of maneuverability to changes in design parameters was analyzed as well. The results showed that the high-speed undersea vehicle with X-shaped full-rudder and cross-shaped fin layout has good maneuverability. When the design parameters change within the constraint range, the dynamic stability of the longitudinal plane Gy and the lateral plane Gz are both above 0.4. The maneuverability of the vehicle as well as the negative buoyancy of the vehicle and the relative position of the center of gravity and the center of buoyancy have a significant impact on the Gy and Gz, and have a negative effect presented; the chord length and the length of the rudder section of the full rudder have the greatest impact on the maneuverability of the vehicle. The rudder section chord length and extension have the greatest influence on the maneuverability of the vehicle, and the full rudder should be designed as a large aspect ratio rudder and installed as close as possible to the tail. -
图 1 常见高速水下航行器流体动力布局
Figure 1. Fluid dynamic layout of common high-speed undersea vehicle
图 5 参数对航行器Gy影响程度Pareto图
Figure 5. Pareto diagram of influence of parameters on Gy of the vehicle
图 7 参数对航行器Rmin的交互影响
Figure 7. Interaction influence of parameters on the Rmin of the vehicle
表 1 航行器尺寸参数符号及含义
Table 1. Symbols and meanings of size parameters of undersea vehicle
符号 含义 符号 含义 $ {X_{fh}} $ 水平鳍板压心距离
前端面距离$\Delta {X_G}$ 重浮心距离, 重心在
浮心前为正LT 水平鳍板后端面距离
前端面距离DE 尾部曲线后部收缩段直径 G 航行器重心 B 航行器浮心 ${R_{\rm{span}}}$ 全动舵展长 ${F_{\rm{span}}}$ 水平鳍展长 ${C_{f{\rm{tip} } }}$ 鳍梢弦长 ${C_{f{\rm{hole} } }}$ 鳍缺口长度 ${C_{\rm{rudder}}}$ 全动舵截面弦长 ${L_{\rm{trail}}}$ 尾部曲线段长度 ${D_{\rm{trail}}}$ 尾部后端面直径 ${L_{\rm{nose}}}$ 头部曲线段长度 $D_F$ 头部平头端面直径 ${\chi _0}$ 鳍板前缘后掠角 
下载: 导出CSV
表 2 设计变量及约束条件
Table 2. Design variables and constraints
输入参数 变量名称 符号 取值范围 输入参数 变量名称 符号 取值范围 常值参数 壳体长度/m LT 1.6 常值参数 鳍厚度/m Tfin 0.005 可调参数 头部前端面直径/m DF [0.05,0.08] 可调参数 航行器重心和浮心距离/m ΔXG [0.005,0.015] 头部曲线可调参数1 $ \sqrt {2R} $ [0,0.5] 尾端面直径/m Dtrail [0.05,0.07] 头部曲线可调参数2 Ksn [4,12] 单块鳍板前缘后掠角/(°) $ {\chi _0} $ [15,30] 尾部曲线可调参数1 Kst [0,0.8] X形舵展长/m Rspan [0.05,0.08] 尾部曲线可调参数2 Kat [2,8] X形舵弦长/m Crudder [0.03,0.06] 鳍梢弦长/m Cftip [0.1,0.15] 鳍板展长/m Lfspan [0.05,0.075] 头部曲线段长度/m Lnose [0.15,0.25] 鳍缺口长度/m Cfhole [0.06,0.08] 尾部曲线段长度/m Ltrail [0.25,0.4] 负浮力范围/N ΔXG [5,25] 尾部端面直径/m Dtrail [0.05,0.06] — — — 输出参数 航行器浮心距前端面距离/m XB — 输出参数 水平面最小回转半径/m Rmin — 纵平面动稳定度 Gy — 侧平面动稳定度 Gz — 平衡攻角/(°) $ {\alpha _0} $ — 平衡舵角/(°) $ \delta _{e0}^{} $ — 鳍压力中心距离前端面距离/m Xfh — 舵力矩中心距离前端面距离/m Lrh —
下载: 导出CSV
-
[1] 孙明芳. 水下火箭的推进原理和应用[J]. 舰载武器, 1995(4): 19-25. [2] 王建儒, 赵仕厂. 水下固体火箭发动机尾流场计算[J]. 固体火箭技术, 2007, 30(5): 388-391.Wang Jianru, Zhao Shichang. Computations for solid rocket moter tail flow underwater[J]. Journal of Solid Rocket Technology, 2007, 30(5): 388-391. [3] Busquets-Mataix J, Busquets-Mataix J V, Busquets-Mataix D. Combined gas-fluid buoyancy system for improved attitude and maneuverability control for application in underwater[J]. IFAC-PapersOnLine, 2015, 48(2): 281-287. doi: 10.1016/j.ifacol.2015.06.046 [4] 黄宇, 林平, 李雨田. 基于单回转体矢量推进AUV的数学建模[J]. 水雷战与舰船防护, 2014, 22(4): 36-40.Huang Yu, Lin Ping, Li Yutian. Mathematical modeling of vector propulsion AUV based on single revolution body[J]. Mine Warfare& Ship Self-defence, 2014, 22(4): 36-40. [5] 黄宇. 基于矢量推进AUV的航行体运动控制研究[D]. 北京: 中国舰船研究院, 2015. [6] 卫民. 基于矢量推进器的AUV运动控制系统研究[D]. 天津: 天津大学, 2012. [7] 郑昆山. 基于喷水矢量推进的水下机器人设计与研究[D]. 长沙: 国防科学技术大学, 2010. [8] 邓岩. 新型喷水推进式水下机器人关键技术研究[D]. 北京: 北京理工大学, 2015. [9] Ba X, Luo X H, Shi Z C. A vectored water jet propulsion method for autonomous underwater vehicles[J]. Ocean Engineering, 2013, 74: 133-140. doi: 10.1016/j.oceaneng.2013.10.003 [10] 王玉, 林秀桃, 宋诗军, 等. 矢量推进自主水下航行器动力学建模及仿真[J]. 天津大学学报: 自然科学与工程技术版, 2014, 47(2): 143-148.Wang Yu, Lin Xiutao, Song Shijun, et al. Dynamic modeling and simulation of autonomous underwater vehicle with vectored thruster[J]. Journal of Tianjin University (Science and Technology), 2014, 47(2): 143-148. [11] 令狐选霞, 徐德民, 唐大军. 水下航行器机动性优化设计的模型研究[J]. 西北工业大学学报, 2003, 21(2): 222-225.Linghu Xuanxia, Xu Demin, Tang Dajun. An optimal model of maneuverability for autonomous under water vehicle[J]. Journal of Northwestern Polytechnical University, 2003, 21(2): 222-225. [12] 肖京平. 水中兵器风洞试验技术[M]. 北京: 国防工业出版社, 2008. [13] Jeon M, Yoon H K, Hwang J. Analysis of the dynamic characteristics for the change of design parameters of an underwater vehicle using sensitivity analysis[J]. International Journal of Naval Architecture and Ocean Engineering, 2018, 10(4): 508-519. [14] Dantas J L D, Barros E A D. Numerical analysis of control surface effects on AUV manoeuvrability[J]. Applied Ocean Research, 2013(42): 168-181. [15] Saeidinezhad A, Dehghan A A, Dehghan M M. Experimental investigation of-hydrodynamic characteristics of a submersible vehicle model with a non-axisymmetric nose in pitch maneuver[J]. Ocean Engineering, 2015, 100: 26-34. doi: 10.1016/j.oceaneng.2015.03.010 [16] Azarsina F, Williams Christopher D. Manoeuvring simulation of the MUN Explorer AUV based on the empirical hydrodynamics of axi-symmetric bare hulls[J]. Applied Ocean Research, 2010(32): 443-453. [17] 张宇文. 鱼雷总体设计理论与方法[M]. 西安: 西北工业大学出版社, 2015. [18] Wang S, Yang M, Wang Y, et al. Optimization of flight parameters for Petrel-L underwater glider[J]. IEEE Journal of Oceanic Engineering, 2021, 46(3): 817-828. doi: 10.1109/JOE.2020.3030573 [19] Wang S, Yang M, Niu W, et al. Multidisciplinary design optimization of underwater glider for improving endurance[J]. Structural and Multidisciplinary Optimization, 2021, 63(6): 2835-51. [20] Bidoki M, Mortazavi M, Sabzehparvar M. A new approach in system and tactic design optimization of an autonomous underwater vehicle by using Multidisciplinary Design Optimization[J]. Ocean Engineering, 2018(147): 517-530. [21] 黄震中. 鱼雷总体设计[M]. 西安: 西北工业大学出版社, 1986. [22] 李天森. 鱼雷操纵性[M]. 北京: 国防工业出版社, 2007. [23] Sun T, Chen G, Yang S, et al. Design and optimization of a bio-inspired hull shape for AUV by surrogate model technology[J]. Engineering Applications of Computational Fluid Mechanics, 2021, 15(1): 1057-74. doi: 10.1080/19942060.2021.1940287 [24] Song Y, Wang Y, Yang S, et al. Sensitivity analysis and parameter optimization of energy consumption for underwater gliders[J]. Energy, 2020, 191: 116506. doi: 10.1016/j.energy.2019.116506 -
点击查看大图
图(10) / 表(2)
计量
- 文章访问数: 202
- HTML全文浏览量: 35
- PDF下载量: 52
- 被引次数: 0
